零知识证明编码入门
- aisiji
- 发布于 2023-02-24 17:34
- 阅读 7693
零知识证明正变得越来越流行,但可能很难找到入门资料。在花了一些时间研究这个主题之后,我整理了我学到的东西,希望它能帮助大家入门零知识证明编程。
 零知识证明正变得越来越流行,但可能很难找到入门资料。在花了一些时间研究这个主题之后,我整理了我学到的东西,希望它能帮助别人。请注意,这是一本初学者指南,因为它的作者(我!)是 ZKP (zero-knowledge proof 零知识证明)编程的初学者,所以如果在本文中发现任何问题,请与我联系!
零知识证明正变得越来越流行,但可能很难找到入门资料。在花了一些时间研究这个主题之后,我整理了我学到的东西,希望它能帮助别人。请注意,这是一本初学者指南,因为它的作者(我!)是 ZKP (zero-knowledge proof 零知识证明)编程的初学者,所以如果在本文中发现任何问题,请与我联系!
本文将介绍什么是零知识证明,如何从开发人员的角度使用它,并用几种语言来编写。不会涉及底层数学:我们把 ZKP 视为加密黑匣子。
什么是零知识证明?
零知识证明(简称 ZKP)是对事实的加密证明,且不会泄露关于该事实的任何信息。
一个介绍 ZKP 的经典例子,我(证明者)可以在不泄露的情况下向你(验证者)证明我知道一个图表的顶点着色(方法)。
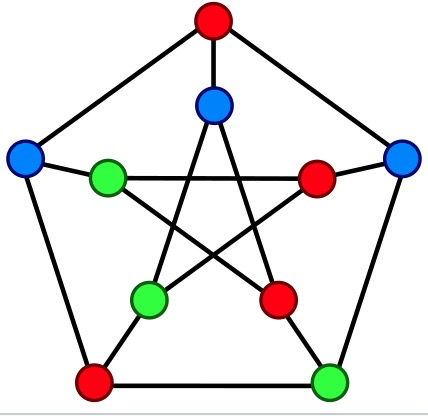
顶点着色:使相邻的两个顶点不具有相同的颜色
为了说明这一点,我们玩一个游戏,我用一组随机颜色为图表着色,并把它遮住,然后你随机选一条边。如果我的着色是有效的,那么这条边连接的两个节点一定是不同颜色。然后我们重复,每次都使用不同的颜色组,直到你满意为止。因为我在每一轮之前都重新绘制图表,所以你不会了解到任何关于着色的信息,但你每次都可以验证它是否有效。
另一个可以被视为 ZKP 的著名示例是数字签名:我可以通过签署一条消息来证明我持有与公钥对应的私钥,并且这个签名不会泄露我的私钥中的任何一位。
什么是 zkSNARK?
SNARK 即 Succinct Non-interactive ARgument of Knowledge。这里的重要部分是前两个单词:succinct(简洁)和non-interactive(非交互性)。
succinct(简洁):意思是证明很简洁证明数据很小。这意味着,无论我们要证明的事实有多复杂,总是可以又快又简单的生成证明。这就是 ZKP 对构建 rollup有吸引力的原因:你可以生成一个简洁的证明,证明 L2 链上发生的所有操作都是有效的,简洁到你可以在 L1 的合约中验证它。像 Mina 这样的协议通过递归证明将这一点发挥到了极致,这使得它们能够通过一个恒定大小的证明来证明整个链历史的有效性。
至于non-interactive(非交互性): 试想一下,如果每次有人需要验证时都需要签名者在线,那么处理签名会有多麻烦。在上面的例子中,图形着色证明是交互式的,需要证明者和验证者之间进行在线游戏。幸运的是,zkSNARK 没有这个要求。
ZKP 各种实现
事实证明,zkSNARK 并不是唯一一种有趣的 ZKP。还有STARK(由 Starkware 首创并用于支撑 Starknet )和 Bulletproofs(用于 Monero)。它们在生成和验证证明的运行时间以及生成的证明大小或对可信设置的需求方面有所不同(下一节将详细介绍)。MatterLabs 对它们进行了详细的比较:
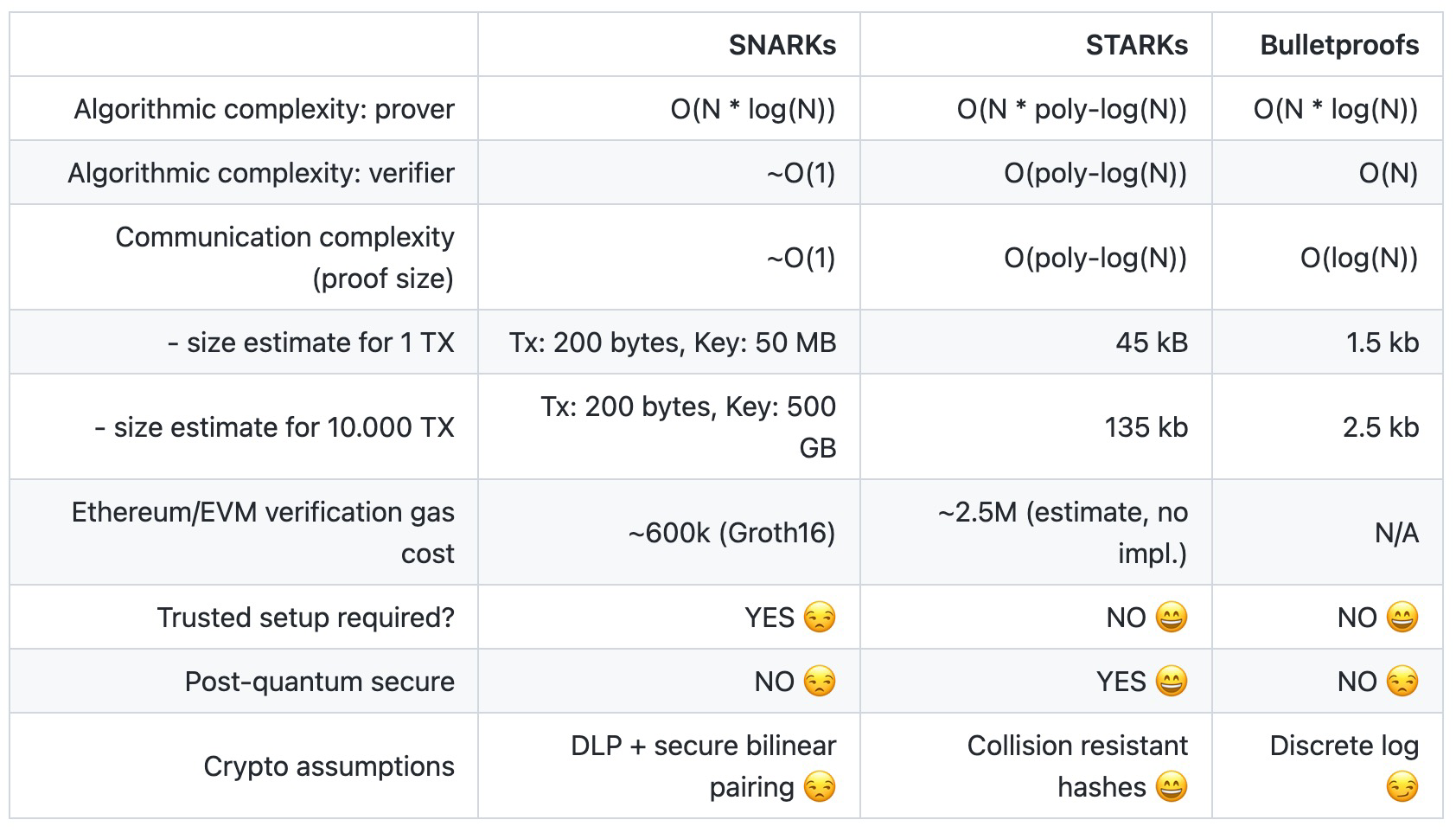
详细参考在这里
即使在 SNARK 中,你也会发现有很多种实现, Groth16 是最受欢迎的之一。PLONK 系列包括 TurboPLONK和UltraPLONK,可以在牺牲证明生成和验证时间的情况下消除对特定电路的信任设置,或者增加对新类型操作的支持。
此外,还有不同的椭圆曲线可供选择,或者可以使用不同的多项式承诺方案。Consensys Gnark 在这里对 SNARK 证明方案和曲线提供了很好的解释。
通常,选择一种 ZKP 语言将决定你最终使用哪个 ZK 后端,尽管有一些像 Circom 或 Gnark 支持多个证明系统。
信任设置
某些类型的证明系统需要所谓的信任设置。信任设置是一次性仪式,由多个参与者运行,以便产生一组随机值,提供给 ZK 证明系统。
这些仪式很关键,因为如果所有参与者串通一气,他们就会破坏证明系统。在这里,破坏证明系统意味着无效声明生成证明也能够被验证者验证通过。幸运的是,只要有一个诚实的参与者就可以达到目的:这就是为什么要呼吁尽可能多的社区成员参加这样的仪式。
某些实现,如 Groth16,需要为每个电路进行信任设置:这意味着,对于编写的每个程序,都需要运行一个新的仪式。其他的,如 PLONK ,只需要一个通用的信任设置,就可以在该风格构建的任何程序上重复使用。而其他的,比如 STARK,根本不需要任何信任设置。
译者注:电路不是指电子电路,电路是指又加法器、乘法器、取反器等算术门组成的逻辑程序。
约束条件
关于 ZKP 的内部机制,需要了解的主要事情是证明在数学约束系统上运行。换句话说,证明者引擎不处理类似的代码x := y * z,而是处理x - y * z = 0形式的约束。根据使用的语言和证明后端的不同,这些可能会影响构建代码的方式。
例如,Circom 只允许在变量上编写二次表达式,而 Halo2 允许编写任何次的多项式约束。正如我们稍后将看到的,用 ZKP 语言编译程序的输出之一将是一组约束。
这意味着某些操作在 ZKP 中比其他操作更容易表示:加法可以在单个约束中表示,而位操作可能需要数百个约束,因为每个位可能需要表示为一个单独的变量。这就是为什么在 ZKP 上工作时通常选择特定加密原语的原因。例如,Pedersen 哈希是一种哈希函数,可以比 keccak 更有效地在算术电路中表示,因此它们经常出现在 ZKP 中。
有限域
需要了解的另一个重要方面是,约束在由基础椭圆曲线确定大小的有限域中运行。这意味着所有算术运算都是以某个特定值为模计算的,这意味着它们将环绕该值。不过不用担心,这个值通常足够大。例如,在 Circom 中它是:
21888242871839275222246405745257275088548364400416034343698204186575808495617这也意味着,如果想为整数变量定义特定的阈值,则需要为其添加额外的约束。某些语言(如 Noir)会自动完成,而其他语言则需要手动完成。
ZKP 为什么有那么多关注?
ZKP 最近引起了很多关注。主要原因是它们可以用作廉价验证任何计算的手段,有效地成为通用密码构建块。
Gubsheep将 ZKP 描述为可编程密码学,从某种意义上说,你可以用它为一般问题编写密码学证明。例如,可以用专门为解决该问题而构建的环签名来证明集合成员身份,或者只是为其编写 zkSNARK 电路。
在零知识 Devcon6 小组中,有一个关于它们在不同系统之间实现互操作性的能力的重要观点:一旦你拥有一个可以验证 ZKP 的系统,那么你就可以验证具有任何计算环境的任何其他系统是否按预期运行,只要你能将其计算表达为 ZKP。这就是 zk-rollup 的力量:如果你可以将你的链规则编写为 ZKP,那么你可以将该证明推送到以太坊并在 EVM 上验证它——即使你的 rollup 不使用 EVM 作为执行环境!
电路是什么样子?
现在让我们看看这一切是如何工作的。第一步是用你选择的 ZK 语言或框架(例如 Circom、Halo2 或 Noir)编写程序。这些程序通常称为电路,它表达了变量集或信号之间的约束。
例如,我们可以用 Circom 构建一个电路,让我们可以证明我们知道满足 c = (a*b)^2 表达式的两个数字a 和b , 而无需透露a 和b :
template MultiplierSq() {
signal input a;
signal input b;
signal ab;
signal output c;
ab <== a * b;
c <== ab * ab;
}这里我们定义了两个私有输入信号、一个中间变量和一个输出值。请注意,由于 Circom 不允许我们编写比二次约束更复杂的内容,因此我们不能直接编写c <== (a*b)^2,这就是我们需要中间ab信号的原因。
创建和验证证明
使用 ZKP 电路的工作流程与常规程序不同,因为我们有两个不同的角色:证明者 和 验证者。甚至在证明者内部,也涉及多个步骤来生成证明,让我们来看看这个过程:
- 首先编写和编译电路。这会输出几个工件(artifacts),例如电路定义的一组约束,以及将在下面的步骤中使用的脚本或二进制文件。
- 根据所使用的 SNARK 实现,可能需要运行信任设置仪式来生成证明和验证密钥,正如其名称所暗示的那样,它们是证明和验证过程所需的加密材料。
- 当与我们的 zk-app 交互时,用户输入电路的私有和公共输入。第一步是用编译期间生成的脚本或二进制文件“执行”电路,就好像它是程序一样。给定输入,将计算所有中间变量和输出变量的值。在上面的示例中,给定
a = 2和b = 3,将计算ab = 6和c = 36。将每个信号分配给它的具体值称为见证(witness)或踪迹(trace)。 - 给定步骤 3 的踪迹和步骤 2 的验证密钥,证明者现在可以生成一个零知识证明,证明电路中定义的所有约束都成立,并且只显示输出值
c。现在可以将此证明发送给验证者。 - 验证者使用提交的证明和验证密钥,现在可以验证证明对于其公共输出是正确的。在我们的例子中,验证者可以加密检查证明者是否知道三个值(
a,b,ab)使得a * b = ab和ab * ab = c,其中c = 36。
请注意,验证步骤很便宜,因此验证者可以作为 EVM 智能合约运行。这允许去信任地验证任何可以表示为 ZKP 的链下计算。
如果你想自己尝试上述工作流程,我强烈推荐Circom 的入门指南,它将指导你完成必要的步骤。在 Circom 中,编译一个电路将输出一个 WASM 或一个计算见证的 C++ 程序,以及一个R1CS 表示,与信任设置仪式一起输出证明和验证密钥。然后,为了生成证明,提供计算出的见证和验证密钥。要验证它,只需用生成的证明和验证密钥。你还可以自动生成 Solidity 合约在链上运行验证。
执行与约束
在上面的工作流程中,你可能已经注意到证明者使用了两次电路:首先是生成见证,然后是导出证明所涵盖的约束。这两次运行是完全不同的,了解它们的区别是理解 ZKP 工作原理的关键之一。
让我们回到之前的 Circom 示例,我们有两条指令:
ab <== a * b;
c <== ab * ab;在 Circom 中,粗箭头(<== )只是赋值和约束这两个不同指令的语法糖,因此上面可以扩展为:
ab <-- a*b
ab === a*b
c <-- ab * ab
c === ab * ab指令a <-- a*b意味着在执行阶段,把a*b赋值给ab,并在编译约束时忽略掉。另一方面,ab === a*b意味着添加一个约束强制ab等于a*b,它在执行期间被忽略。换句话说,在编写电路时,你是在一个程序中编写属于两种不同编程范式的两个不同程序。
虽然通常会编写等效的赋值和约束,但有时需要将它们分开。一个很好的例子就是电路IsZero。
IsZero电路
编写一个如果输入信号为零则输出 1 否则输出 0 的电路非常困难,因为你被二次表达式所限制。如果你正在考虑使用类似x === 0的表达式,请注意,它不会返回x是否为零的布尔值,而在该电路中将信号x限制为零。
幸运的是,Circom 有一个好用的库,包括一个IsZero返回0或1取决于输入是否为零的电路,如下所示:
template IsZero() {
signal input in;
signal output out;
signal inv;
inv <-- in!=0 ? 1/in : 0;
out <-- -in*inv +1;
out === -in*inv +1;
in*out === 0;
}这是在电路中解耦执行和约束的好例子。让我们开始分析约束。约束in * out = 0 告诉我们in 或 out为零。如果in是零,那么out = -in * inv + 1 = 1。如果out为零,则它遵循in * inv = 1,这意味着in不能为零。
但请注意,在我们的推理中从未出现inv的实际值,因为我们不需要它。这对于编写约束是有效的,但是当涉及到填充跟踪时,它就不够用了。我们需要告诉 Circom 如何在见证生成阶段计算inv的值:这就是inv <-- in!=0 ? 1/in : 0表达式的用处。Cairo 恰当地称这种表达式为hints(暗示)。
请注意,我们在这里使用的运算比二次表达式复杂得多:我们有条件、比较和除法。这是因为执行阶段与约束无关,因此不受生成 ZKP 的限制。因此,在执行阶段工作时,我们又回到了非常常见的编程方式,可以访问额外的运算符、控制流语句,甚至辅助函数。
欠缺约束计算漏洞
然而,执行阶段和约束生成阶段之间的这种差异可能会导致非常严重的错误。回到IsZero例子,如果我们忘记写一个约束,比如说in*out = 0,会发生什么?
让我们按照已知的工作流程进行操作,假设in=3输入:
- 电路编译得很好,因为没有错误。
- 见证生成将遵循执行指令,并正确计算值
inv=3^-1, out=0。 - 由于约束成立,证明者会根据见证和公共输出生成证明
out = -in*inv +1。 - 验证者会接受它是有效的,相信证明者有一个私有的非零值。
到目前为止,一切都很好。但是,如果一个恶意的证明者想要让我们相信他们有一个为零的值,而实际in=3,会发生什么呢?
- 恶意用户可以手动制作一个
in=3, inv=0, out=1的见证(witness). - 由于见证(witness)满足约束
out = -in*inv +1,因此证明者可以为其生成证明。 - 验证者欣然接受,认为用户有一个为零的值,而实际上没有。
这种问题被称为欠缺约束计算,特别难以捕捉。任何将电路视为黑盒的单元测试永远不会触发它们,因为它们使用电路的执行逻辑来构建见证(witness),这将通过约束。重现它们的唯一方法是手动组装具有自定义逻辑的见证,这需要你确切地知道正在寻找的攻击是谁。
或者,有一些努力来验证你编写的关于要编码的功能的电路的可靠性,例如Ecne。
这里的底线是,当你编写与约束生成代码分开的执行代码时,应该特别小心,因为它为欠缺约束的 ZK 程序打开了大门。
一个真实世界的例子
Tornado Cash是关于如何使用 Circom 电路构建真实世界的 zk-app 的绝佳学习资源。我强烈建议阅读这个3 页长的白皮书,以及 Gubsheep 在 0xparc 课程中对 Tornado Cash课程的分解,还有 Porter 对该白皮书的概述。
可能你不熟悉 Tornado ,其要点是可以将离散数量的 ETH(有0.1、1、10 和 100 ETH 的票据)存入合约,然后匿名将每张票据资金提取到其他的地址。这可以将你的币与其他人的混合在一起,只要用的足够多就可以匿名。
它是如何工作的?
为了便于解释,我们将通过一个略微简化的协议版本,并遵循 Gubsheep 版本而不是实际实现版本。
每当用户想要存入一笔钱时,都会生成一个秘密的值s,并将他们的 1 ETH 连同秘密的哈希值H(s)一起提交给合约。合约将所有提交的秘密哈希收集到默克尔树中,并存储其根R。
现在,当用户想要取回,需要证明他们拥有与H(s)相对应的秘密。为此,用户提交一个 ZKP,表明他们知道一个私有值s, 这样H(s)就在根R的默克尔树中。没有透露树的哪一个叶子是用户的H(s),因为 ZKP 只有根R是公共输出的,从而保留了匿名性。 默克尔证明是由 ZKP 中的一个电路检查的。
我们还需要一种方法来确保用户不能两次取回同一笔钱。这就是 nullifier 概念的用处。nullifier 是一个值,从初始秘密确定性地生成,并被跟踪防止双花。
因此,除了证明根R的默克尔树成员资格外,ZKP 还输出一个值G(s)用作 nullifier,其中G是另一个不同于H的哈希函数。然后,每当一笔钱被取回时,它的 nullifier 就会被添加到智能合约中的 nullifier 集中,如果它已经存在,则取款被拒绝。请注意,G需要与H不同哈希,否则 ZKP 将泄露H(s),这可以追溯到原始存款并打破匿名性。
换句话说,每当用户想要取款时,他们都会提交一个 ZKP,声明他们知道一个秘密值,这个值在根为 R 的默克尔树中,并公开这个秘密值的 nullifier。然后合约可以检查默克尔根是否匹配并且没有使用 nullifier。
如果阅读了 Tornado 的白皮书,你会注意到 nullifier 概念在他们的实现中与我们现在的描述有不同的地方。Tornado 实际上使用了两个不同的秘密值,称为 randomness
r和 nullifierk,它们存储的公共值称为nullifier hash。Tornado 还使用单个哈希函数(Pedersen 哈希)而不是两个不同的哈希函数,他们将默克尔树叶计算为H(r || k),将 nullifier hash 计算为H(k)。重要的是 nullifier 不能链接回默克尔树叶,并且它确定是从秘密生成的。你可以在这里查看 Tornado 在 Circom 中的完整电路。
ZKP 的语言
你可以选择多种语言和框架来编写 ZK 电路,既可以是通用的(如 Circom),也可以是特定平台的(如 Cairo)。我尝试了三种不同的语言,Circom、Halo2 和 Noir,并实现了相同的电路来进行比较。这个电路证明用户知道一组私下的剪刀石头布比赛的结果,因此总分与公开输出相匹配。分数是按照advent of code 2022 day 2的定义计算的。
总分是每轮得分的总和。单个回合的分数是选择的形状的分数(石头 1 分,布 2 分,剪刀 3 分)加上该回合结果的分数(输了则为 0,平局则为 3 ,如果你赢了,则为 6)。
下面是每种语言的概述,我对它的印象,以及剪刀石头布电路在其中的样子。请记住,我还是所有这些方面的初学者,因此可能存在错误。如果你发现任何问题,请与我联系,以便我修改这篇文章。
我仍然需要尝试的其他语言和框架:Zokrates、Cairo、SnarkyJS、Gnark和Leo。
Circom
正如 CyberPorter所建议的,我发现Circom是开始学习 ZKP 的最佳语言。对我来说,Circom 对学习来说具有理想的抽象级别:级别不是太高,它抽象掉了 ZKP 的一些怪癖,也不是太低让人陷入烦人的细节中。它也已经存在了很长时间了,可以找到更多文档和示例,还有来自 0xparc 的很棒的 Circom 研讨会。最后但同样重要的是,有circomlib,这是一个 Circom 通用的构建库。
Circom 附带一个基于 rust 的编译器 CLI,加上一个用于信任设置、证明生成和验证的npm 包。拥有 npm 包的好处是可以在浏览器中生成证明,从而打开构建 zk-app 的大门。还可以自动生成 Solidity 合约来验证链上的证明。Circom 还允许在 Groth16 和 PLONK 之间选择证明引擎。
如前所述,在 Circom 中,需要组装电路,其中每个电路都有一组输入、内部部件和输出信号。电路被定义为template(模板),它可以用编译时用已知的值进行参数化,这类似于 C++函数模板。Circom也有函数的概念,作为执行阶段的可重复使用的构建块。
主要的挑战是 Circom 是理解你什么时候在写约束生成代码,什么时候在写见证(witness)生成代码,并且保持跟踪什么值是在编译时已知,什么是在运行时才知道的。很多语言构造只可用于见证者生成,例如布尔运算符或比较运算符,或者只能依赖于编译时已知的值,例如控制流语句。此外,记住约束和见证生成时间之间的差异可以防止出现欠缺约束的计算错误。
剪刀石头布的 Circom 实现
用 Circom 编写剪刀石头布问题的电路很有趣。由于不可能在约束中编写条件表达式,因此需要求助于基于数学的技巧。作为一个简单的例子,第一个电路通过检查它是 0、1 或 2 来验证游戏的输入,如下所示:
template AssertIsRPS() {
signal input x;
signal isRP <== (x-0) * (x-1);
isRP * (x-2) === 0;
}下面的代码用类似的结构来计算单轮得分,IsEqual电路来自 CircomLib :
// Returns the score for a single round, given the plays by x and y
template Round() {
signal input x, y;
signal output out;
// ensure that each input is within 0,1,2
AssertIsRPS()(x);
AssertIsRPS()(y);
// check if match was a draw
signal isDraw <== IsEqual()([x, y]);
signal diffYX <== (y+3)-x;
// y wins if y-x = 1 mod 3
signal yWins1 <== (diffYX-1) * (diffYX-4);
signal yWins <== IsZero()(yWins1);
// x wins if y-x = 2 mod 3
signal xWins1 <== (diffYX-2) * (diffYX-5);
signal xWins <== IsZero()(xWins1);
// check that exactly one of xWins, yWins, isDraw is true
// we probably can do without these constraints
signal xOrYWins <== (xWins - 1) * (yWins - 1);
xOrYWins * (isDraw - 1) === 0;
xWins + yWins + isDraw === 1;
// score is 6 if y wins, 3 if draw, 0 if x wins
// plus 1, 2, 3 depending on the choice of RPS
out <== yWins * 6 + isDraw * 3 + y + 1;
}最后,最外层的电路循环遍历可参数化的轮数n,并汇总所有分数。请注意,这里可以使用循环,因为它取决于n,这是编译时已知的模板参数。
template Game(n) {
signal input xs[n];
signal input ys[n];
signal scores[n];
signal output out;
var score = 0;
for (var i = 0; i < n; i++) {
scores[i] <== Round()(xs[i], ys[i]);
score += scores[i];
}
out <== score;
}Halo2
Halo2不是一种语言,而是一个基于 Rust 的框架,由 ZCash 团队维护。Halo2 用于 PLONKish ,让你可以非常直接地控制电路在算术运算中的表示方式。这使得 Halo2 非常低级,但非常适合编写高度优化的电路。
对我来说,Halo2 的学习曲线是迄今为止最陡峭的。不仅仅是因为必须了解 PLONKish 算术如何构建电路,主要是因为我发现 Halo2 的 API 非常复杂并且很难找到文档。学习 Halo2 的资源也很少:我找到的最好的是0xparc 课程,它提供了一些非常有价值的代码示例,以及主程序库中的示例。你还可以查看awesome-halo2获取更新的资源。
在开始使用 Halo2 时,请记住有两种框架:ZCash 维护的vanilla,使用不同的多项式承诺(KZG而不是IPA )的以太坊的隐私和扩展探索团队的分支,这更多的是对以太坊友好。
PLONKish 算术
用 Halo2 构建电路的关键是从设计底层 PLONKish 矩阵开始。在 PLONKish 中,电路是在你直接定义的矩阵上定义的。这个矩阵由多列组成,其中一列可能代表一个公共输出(称为instance),一个私有见证值(称为advice),一个常量值(称为fixed),一个约束是否启用的标志(称为selector,下面有更多内容)或一个查找值(用于查找表,一种高级功能)。
设置好矩阵后,就可以用门(gates)定义多项式约束了。Halo2 中的门定义了应用于矩阵中一组单元格的一个或多个约束。每个门都通过一个选择器(selector)列来控制:如果选择器在一行中启用,那么将强制执行门相对于该行施加的约束。
门(gate)可以定义跨多行的约束。例如,下面有一个直接来自 Halo2 电子书的 L 形乘法门示例:
meta.create_gate("mul", |meta| {
// To implement multiplication, we need three advice cells and a selector
// cell. We arrange them like so:
//
// | a0 | a1 | s_mul |
// |-----|-----|-------|
// | lhs | rhs | s_mul |
// | out | | |
//
// Gates may refer to any relative offsets we want, but each distinct
// offset adds a cost to the proof. The most common offsets are 0 (the
// current row), 1 (the next row), and -1 (the previous row), for which
// `Rotation` has specific constructors.
let lhs = meta.query_advice(advice[0], Rotation::cur());
let rhs = meta.query_advice(advice[1], Rotation::cur());
let out = meta.query_advice(advice[0], Rotation::next());
let s_mul = meta.query_selector(s_mul);
// Finally, we return the polynomial expressions that constrain this gate.
// For our multiplication gate, we only need a single polynomial constraint.
//
// The polynomial expressions returned from `create_gate` will be
// constrained by the proving system to equal zero. Our expression
// has the following properties:
// - When s_mul = 0, any value is allowed in lhs, rhs, and out.
// - When s_mul != 0, this constrains lhs * rhs = out.
vec![s_mul * (lhs * rhs - out)]
});在上面的代码示例中,a0和a1是建议列, s_mul是定义是否执行mul乘法门的选择器。如果是,则下一行中a0的值将被限制为等于当前行的a0和a1的乘积。
此外,Halo2 允许定义等式约束,要求矩阵中的特定单元格必须与另一个单元格相等。这对于在矩阵中“复制”值是很有用的,或者为了公开一个值而约束一个公共实例单元等于特定的私有advice单元很有用。
作为另一个示例,你可以定义一个电路来证明第 N 个斐波那契数,矩阵的第i行有值x[i-2], x[i-1], x[i]。这意味着首先需要三个advice列,我们称它们为a, b, c。然后,你应该用一个门在同一行中约束c等于a + b,这需要添加一个选择器列来控制它。并且必须设置相等约束,让上一行的a+b=b+c。最后,为了将第 N 个数字公开为公共值,需要一个实例列,约束为等于最后一行的值c。
Chip、 gadget 和 region
Halo2 中电路的主要构建块是 gadget 和 Chip 。Chip是最低级别的单位。Chip 通常会公开一种配置门的方法,以及在合成过程为单元(cell)赋值的多种方法。还可以构建由其他 Chip 组成的 Chip。另一方面,gadget 在更高的抽象级别上运行,隐藏了底层 Chip 的实现细节,尽管可以直接用 Chip 构建电路并完全跳过 gadget。
为了提高可重用性,你会注意到 Chip 总是在相对偏移量上运行。这允许将多个 Chip 分组到电路中的不同region(区域)。一旦定义了所有 region 及其形状,FloorPlanner 就会在矩阵上排列这些 region ,因此你无需直接定义每个 Chip 的实际放置位置。然而,根据构建电路的方式,完全有可能将所有内容打包到一个 region 中,而不是将布局委托给 planner。
Halo2 Rust API
在 Halo2 中,与 Circom 类似,要记住的主要事情是你的代码将在不同情况下被多次调用:无论是配置矩阵、生成约束、创建证明还是计算见证。
你的电路需要实现一个特定的Circuit trait用来定义方法,在整个生命周期中调用,可以是具体的,也可以是未知Value :
pub trait Circuit<F: Field> {
type Config: Clone;
type FloorPlanner: FloorPlanner;
fn without_witnesses(&self) -> Self;
fn configure(meta: &mut ConstraintSystem<F>) -> Self::Config;
fn synthesize(
&self,
config: Self::Config,
layouter: impl Layouter<F>
) -> Result<(), Error>;
}这里的重要部分是configure和synthesize。简单来说是configure设置矩阵形状和它的门,synthesize计算见证并使用相应的值填充矩阵。但是,synthesize也可能在其他阶段被未知值调用,因此你需要始终使用包装好的Value。例如,虽然看起来有悖常理,但门中的多项式约束是在配置期间定义的,而等式约束是在 synthesize 设置的。
Halo2 书中的示例很好地逐步介绍了如何使用单 Chip 实现简单电路,以防你还需要一个脚手架。
石头剪刀布的 Halo2 实现
石头剪刀布的 Halo2 实现比 Circom 要冗长得多,我们在这里只重现一些部分。首先,矩阵设置有以下列:
- 两个玩家各自的 advice 列,
xs和ys,行中的值i表示玩家在回合i中的选择。 - 第三个 advice 列
accum,跟踪累积总分,因此行i包含之前所有回合的分数总和. - 一个公共实例列,最后一个单元(cell)被限制为等于
accum的值,因此只显示总分而不显示中间分。 - 一个选择器(selector),用于启用验证输入并计算每轮分数的单个门。
主chip定义了一个自定义门,它包含每一轮的所有约束:验证输入是否在范围内,计算该轮的分数并将其添加到累计总分中。该 chip 用一行中xs、ys和accum的值作为“输入”,并在下一行的列accum中“输出”新的分数。
meta.create_gate("round", |meta| {
let s = meta.query_selector(selector);
let x = meta.query_advice(col_x, Rotation::cur());
let y = meta.query_advice(col_y, Rotation::cur());
let accum = meta.query_advice(col_accum, Rotation::cur());
// We store the output in the accum column in the next row
let out = meta.query_advice(col_accum, Rotation::next());
// Constraints for each round
vec![
// out = y_wins * 6 + is_draw * 3 + y + 1 + accum
s.clone() * (out - (y_wins.expr() * F::from(6) + is_draw.expr() * F::from(3) + y.clone() + const_val(1) + accum)),
// x in (0,1,2)
s.clone() * x.clone() * (x.clone() - const_val(1)) * (x.clone() - const_val(2)),
// y in (0,1,2)
s.clone() * y.clone() * (y.clone() - const_val(1)) * (y.clone() - const_val(2)),
]
});上面的y_wins和is_draw是如下定义的IsZero chip 。请注意,我们可以所有约束使用相同的选择器列,因为没有哪一行需要启用某些约束禁用其他约束。
// yWins <==> (y+2-x) * (y-1-x) == 0;
let y_wins = IsZeroChip::configure(
meta,
|meta| meta.query_selector(selector),
|meta| {
let x = meta.query_advice(col_x, Rotation::cur());
let y = meta.query_advice(col_y, Rotation::cur());
(y.clone() + const_val(2) - x.clone()) * (y - const_val(1) - x)
}
);在整合电路时,循环遍历每一轮输入,计算累积分数,并将计算出的值分配给矩阵。注意,对于“执行”模式,我们可以直接使用条件表达式来计算分数。
// Assign one row per round
for row in 0..N {
let [x, y] = [xs[row], ys[row]];
// Enable the selector for the round gate
self.config.selector.enable(&mut region, row)?;
// This is requiring us to add a constant column to the chip config just with zeros
if row == 0 {
region.assign_advice_from_constant(|| "zero", col_accum, 0, F::ZERO)?;
}
// Set x and y advice columns to the input values
region.assign_advice(|| format!("x[{}]", row),col_x,row,|| x)?;
region.assign_advice(|| format!("y[{}]", row),col_y,row,|| y)?;
// Assign the is_zero chips to the same expressions defined in the gates
// yWins <==> (y+2-x) * (y-1-x) == 0;
let y_wins_chip = IsZeroChip::construct(y_wins.clone());
let y_wins_value = (y + Value::known(F::from(2)) - x) * (y - Value::known(F::ONE) - x);
let y_wins = y_wins_chip.assign(&mut region, row, y_wins_value)?;
// isDraw <==> y-x == 0;
let is_draw_chip = IsZeroChip::construct(is_draw.clone());
let is_draw_value = y - x;
let is_draw = is_draw_chip.assign(&mut region, row, is_draw_value)?;
// Calculate the score of this round
let round_score = y_wins.zip(is_draw).and_then(|(y_wins, is_draw)| {
let partial_score = if y_wins { 6 } else if is_draw { 3 } else { 0 };
Value::known(F::from(partial_score)) + y + Value::known(F::ONE)
});
// Assign the col_accum *in the next row* to the new score
accum_value = accum_value + round_score;
out_cell = region.assign_advice(
|| format!("out[{}]", row),
col_accum,
row + 1,
|| accum_value
);
};最后一位是通过约束实例列来匹配矩阵最后一行中的列accum,将总分作为电路的公共输出:
layouter.constrain_instance(out_cell.cell(), self.config.instance, N-1)Noir
Noir 由 Aztec 构建,是最新的语言,并且正在积极开发中。它有称为nargo,一个基于 rust 的 CLI和一组npm 包。npm 包的发布似乎略微落后于 crate 包,它具有最先进的功能,并且在几天前(2 月初)才发布了第一个稳定版本。rust crate包 和 npm 包都可以用来编译 Noir 程序,生成和验证证明,以及创建验证的 Solidity 合约。
Noir 深受 Rust 的启发,因为它们有几乎相同的语法。支持整数、布尔值、元组、结构和数组,以及一个基础field类型,用来表示证明后端的原生字段中的元素(想想一个上限为大约 254 位的大质数的无符号整数),并且性能比常规整数更好。
与 Circom 不同,Noir 不允许定义仅用于见证生成(也称为hint暗示)的代码。Noir 支持开箱即用的控制流语句和运算符,并根据需要将它们转换为等效约束。这有助于以牺牲性能为代价防止任何不受约束的计算错误。也就是说,你可以使用特定的constrain关键字定义与见证生成无关的约束。
剪刀石头布的 Noir 实现
与其他语言相比,Noir 感觉有点像作弊,因为它抽象掉了与 ZKP 相关的大部分复杂性,感觉就像在编写常规的 Rust 代码。整个程序只有 30 行,读起来就像一个常规程序:
global N: Field = 3;
#[builtin(arraylen)]
fn len<T>(_input : [T]) -> comptime Field {}
fn round(x: Field, y: Field) -> Field {
constrain (x as u8) <= 2;
constrain (y as u8) <= 2;
let mut score = 0;
let diffYX = (y + 3 - x);
if x == y {
score = 3;
}
if (diffYX == 4) | (diffYX == 1) {
score = 6;
}
score + y + 1
}
fn main(xs: [Field; N], ys: [Field; N]) -> pub Field {
let mut result = 0;
for i in 0..len(xs) {
result = result + round(xs[i], ys[i]);
}
result
}值得一提的是,我没有对每种语言生成的约束数量进行任何分析,但预计 Noir 具有更高的抽象级别,会产生更多的约束,这会影响证明时间。然而,随着编译器的成熟,应该会添加更多的优化,这些优化会自动合并到 Noir 编写的程序中。
资源
如果你还想继续学习,这里有一些我用来加速学习 ZKP 的资源。
- CyberPorter的课程,提供了对 ZKP 的一个很好的概述,包括动机、空间映射和谁在做它、深入了解 TornadoCash、Circom、Cairo、SnarkyJS 和 Noir 的概述,以及Groth16 背后的数学演练。
- 0xPARC有两门完整的在线课程,一门关于 Circom,另一门关于 Halo2。我强烈建议从 Circom 开始,主要由Gubsheep主导,他是Dark Forest 游戏的幕后大佬。这些课程包括实践研讨会,可指导你逐步了解如何构建多个电路。如果你想尝试一下 Halo2,我会说它们是必看的,因为上面没有太多其他资源。
- Vitalik有多篇博客文章,几乎涵盖了理解 SNARK 和 STARK 所需的每个加密概念,以及该技术的有趣用途。如果你想更深入地了解 ZKP 的工作原理,请先在他的博客上搜索。
- 正在构建 ZK-EVM 的Scroll 团队在谈到 ZKP 时运营了一个优秀的教育博客。特别是,关于证明生成的文章提供了创建 ZKP 时涉及的整个工作流程的重要步骤。
- zkSync 背后的团队Matter Labs维护了一个很棒的零知识证明列表,其中包含指向各种资源的链接。
原文链接:https://dev.to/spalladino/a-beginners-intro-to-coding-zero-knowledge-proofs-c56
- ZK编年史:哈希登场 168 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 372 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 293 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 388 浏览
- Zcash:比特币遗忘的隐私 438 浏览
- ZK编年史:计算模型 308 浏览
- lambdaworks 2026 年更新路线图和优先级 376 浏览
- 2026年构建机构级DeFi平台真正需要什么 924 浏览
- zkMesh:2026年1月回顾 462 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 660 浏览
- Zcash 的时代到来了 793 浏览
- ZK 编年史:电路(第二部分) 429 浏览

