Polocolo介绍：一种利用查找表的PLONK零知识友好型哈希函数（第一部分）

我设计了一种新的 ZK 友好的哈希函数：Polocolo↗。

传统的哈希函数在零知识 (ZK) 证明设置中通常效率低下，因此导致了多种 ZK 友好哈希函数的设计。另一方面，lookup arguments 最近被纳入 ZK 协议中，从而能够更有效地处理 ZK 不友好 的操作。因此，已经提出了基于 lookup table 的 ZK 友好哈希函数。

Polocolo 针对的是 PlonKup↗，它是 PLONK↗ 的扩展，具有 plookup↗。与最先进的 ZK 友好哈希函数相比，Polocolo 需要更少的 PLONK gate。例如，当 t=8t = 8t=8 时，Polocolo 比 Anemoi↗ 需要少 21% 的 PLONK gate，Anemoi 是目前最高效的 ZK 友好哈希函数，其中 ttt 表示底层置换的大小。对于 t=3t = 3t=3，Polocolo 比 Reinforced Concrete↗ 需要少 24% 的 PLONK gate，Reinforced Concrete 是近期基于 lookup 的 ZK 友好哈希函数之一。Polocolo 已在 Eurocrypt 2025↗ 上展示。

本文的第一部分讨论了 PLONK 和 PlonKup 的理论基础。在建立了这些基础之后，我们将在第二部分中在此基础上探讨 Polocolo 的具体工作原理。

ZK 友好哈希函数回顾

之前，我们在 “ ZK-Friendly Hash Functions↗” 和 “ Algebraic Attacks on ZK-Friendly Hash Functions↗” 两篇文章中讨论了 ZK 友好哈希函数以及针对它们的代数攻击。对于那些没有读过这些文章的人，这里有一个简短的总结。

哈希函数在 ZK 协议中用于密码学目的，例如承诺方案和伪随机数生成。虽然 SHA-2 和 SHA-3 已经标准化并被广泛研究，但它们在 ZK 协议中的效率非常低，因为按位操作——虽然在传统 CPU 上速度很快——但不太适合 ZK 证明系统。这种低效率促使了 ZK 友好哈希函数的发展，这些函数针对 ZK 设置中的性能进行了优化。

直观地说，ZK 友好哈希函数优先考虑代数简单性。我们在 之前的文章↗ 中介绍了 MiMC↗、Poseidon↗、Vision↗ 和 Rescue↗。此外，Anemoi↗、Griffin↗ 和 Arion↗ 等较新的提案已经涌现，成为先进的 ZK 友好哈希函数。

Sponge Construction（海绵结构）

设计 ZK 友好哈希函数的常用方法是首先构造一个置换（一个双射函数 Fpt→Fpt\mathbb{F}_p^t \rightarrow \mathbb{F}_p^tFpt​→Fpt​, 其中 ttt 表示置换的大小），然后使用 海绵结构↗ 将其转换为哈希函数。

海绵结构 — PiP_iPi​ 是输入，ZiZ_iZi​ 是哈希输出。未使用的 容量 ccc 应该是所需防碰撞或原像攻击的两倍。图片来自 Wikipedia↗。

海绵结构分两个阶段运行：

1. 吸收阶段。 处理消息块并将其集成到内部状态中。
2. 挤压阶段。 从状态中提取哈希摘要。

这种框架的关键优势包括

• 任意输入/输出长度——支持哈希函数的可变长度输入和输出。
• 可证明的安全性——海绵结构的安全性被正式降低到基础置换的安全性。

从设计者的角度来看，主要任务简化为优化置换的结构。

Algebraic Attacks（代数攻击）

如果置换是理想的置换（置换的输出是均匀随机的），则通过海绵结构导出的哈希函数是安全的。然而，现实世界的置换使用确定性的数学结构；置换的输出不是随机的。输出中的任何偏差都可能导致对哈希函数的攻击。

针对 ZK 友好哈希函数的攻击侧重于 constrained-input constrained-output (CICO) problem（约束输入约束输出问题）。对于置换 P:Fpt→FptP : \mathbb{F}_p^t \rightarrow \mathbb{F}_p^tP:Fpt​→Fpt​, CICO 问题涉及找到 x1,…,xt−1,y1,…,yt−1∈Fpx_1, \dots, x_{t-1}, y_1, \dots, y_{t-1} \in \mathbb{F}_px1​,…,xt−1​,y1​,…,yt−1​∈Fp​，使得 P(x1,…,xt−1,0)=(y1,…,yt−1,0).P(x_1, \dots, x_{t-1}, 0) = (y_1, \dots, y_{t-1}, 0).P(x1​,…,xt−1​,0)=(y1​,…,yt−1​,0). 解决这个问题可以实现对哈希函数的碰撞或原像攻击。

一个简单的暴力攻击，不使用 PPP 的特性，是任意设置 x1,…,xt−1x_1, \dots, x_{t-1}x1​,…,xt−1​，并检查 P(x1,…,xt−1,0)P(x_1, \dots, x_{t-1}, 0)P(x1​,…,xt−1​,0) 的最后一个元素是否为零。这需要 O(∣Fp∣)=O(p)O(\vert \mathbb{F}_p \vert) = O(p)O(∣Fp​∣)=O(p) 次尝试。如果 CICO 问题可以比 O(2κ)O(2^\kappa)O(2κ) 更快地解决，对于某个安全参数 κ\kappaκ，则从该置换导出的哈希函数被认为是不安全的。在 ZK 友好哈希函数中，设计者通常考虑 κ=128\kappa=128κ=128，这意味着预期的攻击复杂度至少为 21282^{128}2128。

在 ZK 友好哈希函数中，函数在代数上很简单。因此，将 CICO 问题表示为方程组并求解它的代数攻击通常是对 ZK 友好哈希函数最有效的攻击。我们在 之前的文章↗ 中介绍了几种攻击。

设计者在考虑了所有提出的攻击（包括安全裕度）后，仔细选择他们的结构和参数。不幸的是，随着攻击技术的不断发展，提出的 ZK 友好哈希函数被攻击是很常见的，即使该哈希函数经过同行评审并在顶级会议上介绍。

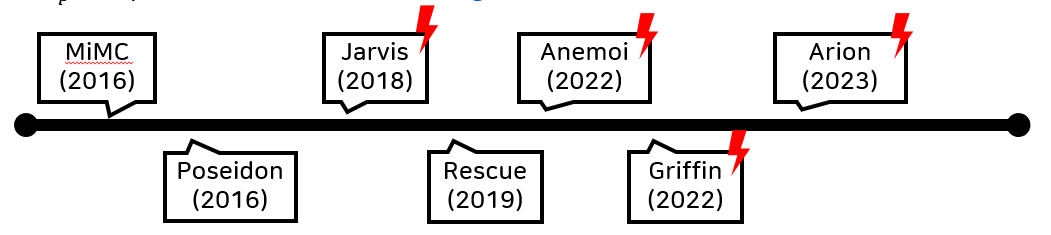这是 ZK 友好哈希函数的时间线。红色闪光标志表示原始规范已被代数攻击破坏。

PLONK 的工作原理是什么？

PLONK↗ 是一种通用且简洁的 ZK 协议。在各种 ZK 协议中，我们将重点关注 PLONK，因为 Polocolo 针对的是带有 lookup 的 PLONK。

零知识证明系统是证明者和验证者之间的双向密码协议，它允许证明者在不泄露自身知识的情况下说服验证者。例如，给定一个哈希函数 hhh 和哈希值 yyy，证明者可以说服验证者他们知道原像 xxx，使得 h(x)=yh(x) = yh(x)=y。该协议的性能指标（包括证明者时间、验证者时间和证明大小）受函数 hhh 的影响。一般来说，hhh 在代数上表达得越简单，协议就越有效。

将 PLONK 与 Groth16↗ 相比，证明大小和验证者复杂度仍然保持 O(1)O(1)O(1)（虽然效率略低），并且结构化参考字符串 (SRS) 是通用的且可更新的。因此，可信设置可以以 通用方式 执行。在 Groth16 中，必须为每个电路执行可信设置。PLONK 也有几个变体，例如 HyperPlonk↗ 和 PlonKup↗，它们分别支持自定义 gate 和 lookup gate。然而，与 Groth16 和 zkSTARK 不同，加法不是免费的。此外，PLONK 缺乏抗量子性。

让我们通过探索它的算术化技术来深入研究 PLONK 的工作原理。这将使我们深入了解证明者的复杂度是如何确定的。

Arithmetization（算术化）

PLONK 采用自己的算术化技术。对于给定的算术电路，有两种类型的约束，gate constraint（门约束）和 copy constraint（复制约束）。

这是一个证明 x,yx, yx,y 知识的例子，使得 x3+xy=14x^3 + xy = 14x3+xy=14。请注意，x=2,y=3x = 2, y = 3x=2,y=3 满足该方程。相应方程的算术电路如下所示。

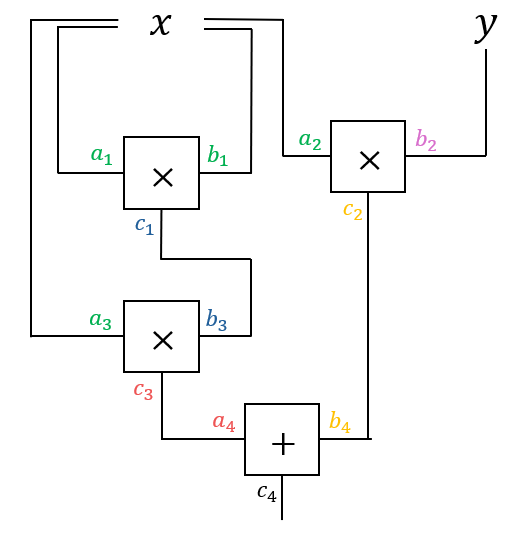方程 x3+xy=14x^3 + xy = 14x3+xy=14 的算术电路。

分别地，ai,bia_i, b_iai​,bi​ 代表左输入和右输入，而 cic_ici​ 代表每个第 iii 个 gate 的输出。每个变量的颜色表示其分配的值，这意味着共享相同颜色的变量具有相同的值。

现在证明者必须证明这两个约束：

1. 对于 gate constraint，对于每个 gate 的输入 ai,bia_i, b_iai​,bi​ 和输出 cic_ici​，该 gate 是有效的（即，ci=ai+bic_i = a_i + b_ici​=ai​+bi​ 对于加法 gate，而 ci=ai×bic_i = a_i \times b_ici​=ai​×bi​ 对于乘法 gate）。
2. 对于 copy constraint，如果颜色相同，则值相同（即 a1=b1=a2=a3,c1=b3,…a_1 = b_1 = a_2 = a_3, c_1 = b_3, \dotsa1​=b1​=a2​=a3​,c1​=b3​,…）。

如果两个约束都得到验证，则验证者确信证明者知道 x,yx, yx,y 使得 x3+xy=14x^3 + xy = 14x3+xy=14。

注意： 实际协议使用数学构建块，如 vanishing polynomials、FFT 和 polynomial commitments。为了简化理解，此解释侧重于 PLONK 的核心概念，而不是完全按照论文中的描述复制协议。有关深入的详细信息，请参阅 原始 PLONK 论文↗。

Gate Constraint（门约束）

对于 gate constraint，每个 gate 由以下等式表示： (qLi)ai+(qRi)bi+(qOi)ci+(qMi)aibi+qCi=0.(q_{L_i})a_i + (q_{R_i})b_i + (q_{O_i})c_i + (q_{M_i})a_ib_i + q_{C_i} = 0. (qLi​​)ai​+(qRi​​)bi​+(qOi​​)ci​+(qMi​​)ai​bi​+qCi​​=0.

selectors (qLi,qRi,qOi,qMi,qCi)(q_{L_i}, q_{R_i}, q_{O_i}, q_{M_i}, q_{C_i})(qLi​​,qRi​​,qOi​​,qMi​​,qCi​​) 由 gate 类型确定。在我们的例子中，四个 gate 配置如下：

0⋅a1+0⋅b1+1⋅c1+(−1)⋅a1b1+0=00⋅a2+0⋅b2+1⋅c2+(−1)⋅a2b2+0=00⋅a3+0⋅b3+1⋅c3+(−1)⋅a3b3+0=0(−1)⋅a4+(−1)⋅b4+0⋅c4+(0)⋅a4b4+(−14)=0\begin{aligned} 0 \cdot a_1 + 0 \cdot b_1 + 1 \cdot c_1 + (-1) \cdot a_1b_1 + 0 &= 0 \\ 0 \cdot a_2 + 0 \cdot b_2 + 1 \cdot c_2 + (-1) \cdot a_2b_2 + 0 &= 0 \\ 0 \cdot a_3 + 0 \cdot b_3 + 1 \cdot c_3 + (-1) \cdot a_3b_3 + 0 &= 0 \\ (-1) \cdot a_4 + (-1) \cdot b_4 + 0 \cdot c_4 + (0) \cdot a_4b_4 + (-14) &= 0 \\ \end{aligned}0⋅a1​+0⋅b1​+1⋅c1​+(−1)⋅a1​b1​+00⋅a2​+0⋅b2​+1⋅c2​+(−1)⋅a2​b2​+00⋅a3​+0⋅b3​+1⋅c3​+(−1)⋅a3​b3​+0(−1)⋅a4​+(−1)⋅b4​+0⋅c4​+(0)⋅a4​b4​+(−14)​=0=0=0=0​

类似于 Groth16↗，证明者构造一个多项式 qL(x)q_L(x)qL​(x)，使得 qL(i)=qLiq_L(i) = q_{L_i}qL​(i)=qLi​​ 对于 i∈{1,2,3,4}i \in \{1,2,3,4\}i∈{1,2,3,4}。多项式 qR(x),qO(x),qM(x),qC(x),a(x),b(x),c(x)q_R(x), q_O(x), q_M(x), q_C(x), a(x), b(x), c(x)qR​(x),qO​(x),qM​(x),qC​(x),a(x),b(x),c(x) 也以类似的方式导出。然后组合约束为 qL(x)a(x)+qR(x)b(x)+qO(x)c(x)+qM(x)a(x)b(x)+qC(x)=0q_L(x)a(x) + q_{R}(x)b(x) + q_{O}(x)c(x) + q_{M}(x)a(x)b(x) + q_{C}(x) = 0qL​(x)a(x)+qR​(x)b(x)+qO​(x)c(x)+qM​(x)a(x)b(x)+qC​(x)=0 对于 x∈{1,2,3,4}x \in \{1,2,3,4\}x∈{1,2,3,4}。

Copy Constraint（复制约束）

对于 copy constraint，证明者必须证明以下等式：

a1=a2=a3=b1,b3=c1,a4=c3,b4=c2.\begin{aligned} & a_1 = a_2 = a_3 = b_1, \\ & b_3 = c_1, \\ & a_4 = c_3, \\ & b_4 = c_2. \\ \end{aligned}​a1​=a2​=a3​=b1​,b3​=c1​,a4​=c3​,b4​=c2​.​

涉及两个以上变量的等式可以分解为成对约束： a1=a2=a3=b1⇔a1=a2,a2=a3,a3=b1.a_1 = a_2 = a_3 = b_1 \Leftrightarrow a_1 = a_2, a_2 = a_3, a_3 = b_1.a1​=a2​=a3​=b1​⇔a1​=a2​,a2​=a3​,a3​=b1​.

为了形式化这一点，定义两个向量 vvv 和 v′v'v′，它们表示原始变量赋值和置换变量赋值：

v=[a1,a2,a3,a4,b1,b2,b3,b4,c1,c2,c3,c4]v′=[a2,a3,b1,c3,a1,b2,c1,c2,b3,b4,a4,c4].\begin{aligned} v &= [a_1, a_2, a_3, a_4, b_1, b_2, b_3, b_4, c_1, c_2, c_3, c_4] \\ v' &= [a_2, a_3, b_1, c_3, a_1, b_2, c_1, c_2, b_3, b_4, a_4, c_4]. \end{aligned}vv′​=[a1​,a2​,a3​,a4​,b1​,b2​,b3​,b4​,c1​,c2​,c3​,c4​]=[a2​,a3​,b1​,c3​,a1​,b2​,c1​,c2​,b3​,b4​,a4​,c4​].​

如果 v=v′v = v'v=v′，则所有需要的等式都成立。为了同时验证整个置换，定义一个置换函数 σ:{1,…,12}→{1,…,12}\sigma : \{1,\dots,12\} \rightarrow \{1,\dots,12\}σ:{1,…,12}→{1,…,12}，其中 σ(i)\sigma(i)σ(i) 表示 v′v'v′ 中元素 v[i]v[i]v[i] 的索引。例如，v[1]=a1v[1] = a_1v[1]=a1​ 映射到 v′[5]v'[5]v′[5]。因此，σ(1)=5\sigma(1) = 5σ(1)=5。

证明者必须证明 v[i]=v′[σ(i)]=v[σ(i)]v[i] = v'[\sigma(i)] = v[\sigma(i)]v[i]=v′[σ(i)]=v[σ(i)] 对于每个 i∈{1,…,12}i \in \{1, \dots, 12\}i∈{1,…,12}。证明者不是直接检查相等性，而是证明 ∏i∈{1,…,12}v[i]+i⋅β+γv[i]+σ(i)⋅β+γ=1 \prod_{i \in \{1,\dots,12\}} \frac{v[i] + i \cdot \beta + \gamma}{v[i] + \sigma(i) \cdot \beta + \gamma} = 1∏i∈{1,…,12}​v[i]+σ(i)⋅β+γv[i]+i⋅β+γ​=1

对于随机 β,γ\beta, \gammaβ,γ。很容易看出，有效的置换确保分子和分母项成对抵消。例如，与 i∈{1,2,3,5}i \in \{1,2,3,5\}i∈{1,2,3,5} 对应的项（链接到 a1=a2=a3=b1a_1 = a_2 = a_3 = b_1a1​=a2​=a3​=b1​）产生：

(a1+β+γ)⋅(a2+2β+γ)⋅(a3+3β+γ)⋅(b1+5β+γ)(a1+5β+γ)⋅(a2+β+γ)⋅(a3+2β+γ)⋅(b1+3β+γ).\frac{(a_1 + \beta + \gamma) \cdot (a_2 + 2\beta + \gamma) \cdot (a_3 + 3\beta + \gamma) \cdot (b_1 + 5\beta + \gamma)}{(a_1 + 5\beta + \gamma) \cdot (a_2 + \beta + \gamma) \cdot (a_3 + 2\beta + \gamma) \cdot (b_1 + 3\beta + \gamma)}.(a1​+5β+γ)⋅(a2​+β+γ)⋅(a3​+2β+γ)⋅(b1​+3β+γ)(a1​+β+γ)⋅(a2​+2β+γ)⋅(a3​+3β+γ)⋅(b1​+5β+γ)​.

如果 a1=a2=a3=b1a_1 = a_2 = a_3 = b_1a1​=a2​=a3​=b1​，则分数简化为 111。

令多项式 f,gf, gf,g 定义为 f=v[i]+i⋅β+γf = v[i] + i \cdot \beta + \gammaf=v[i]+i⋅β+γ 且 g=v[i]+σ(i)⋅β+γg = v[i] + \sigma(i) \cdot \beta + \gammag=v[i]+σ(i)⋅β+γ， 分别。

定义一个多项式 ppp 为 p(1)=1p(1) = 1p(1)=1 且 p(i)=∏j<if(j)g(j)p(i) = \prod_{j < i} \frac{f(j)}{g(j)}p(i)=∏j<i​g(j)f(j)​ 对于 i∈{2,…,12}i \in \{2,\dots,12\}i∈{2,…,12}。

然后

p(1)=1,p(x+1)=g(x)p(x)f(x) 对于 x∈{1,…,11},p(12)=1\begin{align} & p(1) = 1, \\ & p(x+1) = \frac{g(x)p(x)}{f(x)} \textrm{ for } x \in \{1,\dots,11\}, \\ & p(12) = 1 \\ \end{align}​p(1)=1,p(x+1)=f(x)g(x)p(x)​ 对于 x∈{1,…,11},p(12)=1​​

必须成立。

通过累积 gate constraint 和 copy constraint，证明者需要证明

qL(x)a(x)+qR(x)b(x)+qO(x)c(x)+qM(x)a(x)b(x)+qC(x)=0 对于 x∈{1,…,4},p(1)=1,p(x+1)=g(x)p(x)f(x) 对于 x∈{1,…,11},p(12)=1.\begin{align} & q_L(x)a(x) + q_{R}(x)b(x) + q_{O}(x)c(x) + q_{M}(x)a(x)b(x) + q_{C}(x) = 0 \textrm{ for } x \in \{1,\dots,4\}, \\ & p(1) = 1, \\ & p(x+1) = \frac{g(x)p(x)}{f(x)} \textrm{ for } x \in \{1,\dots,11\}, \\ & p(12) = 1. \\ \end{align}​qL​(x)a(x)+qR​(x)b(x)+qO​(x)c(x)+qM​(x)a(x)b(x)+qC​(x)=0 对于 x∈{1,…,4},p(1)=1,p(x+1)=f(x)g(x)p(x)​ 对于 x∈{1,…,11},p(12)=1.​​

函数 qL,qR,qO,qM,q_L, q_R, q_O, q_M,qL​,qR​,qO​,qM​ 和 qCq_CqC​ 由电路确定并公开计算，而函数 a,b,c,a, b, c,a,b,c 和 ppp 从证明者的私有 witness 派生而来。这些等式可以使用数学构建块（如 vanishing polynomials、FFT 和 polynomial commitments）有效地验证。本文中省略了详细的解释。

需要注意的重要一点是多项式 qL,qR,qO,qM,qC,a,b,c,q_L, q_R, q_O, q_M, q_C, a, b, c,qL​,qR​,qO​,qM​,qC​,a,b,c 和 ppp 的次数由 gate 的数量决定。因此，证明者的复杂度 与 gate 的数量 成正比。

PlonKup 的工作原理是什么？

PLONK 面临一个常见的挑战：在原生域 Fp\mathbb{F}_pFp​ 中，高次运算需要大量的开销。这导致发明了 PLONK 的一个扩展，名为 PlonKup↗。

在普通的 PLONK 中，证明者可以使用加法和乘法 gate。PlonkUp 支持一种额外的 gate 类型：lookup gate。使用 lookup gate，证明者可以证明 witness xxx 属于公共表 TTT。

在 PlonKup 中，gate constraint 通过引入一个用于 lookup gate 的新 selector qKq_KqK​ 来扩展。对于公共表 TTT 中的第 iii 个元素 (xi,yi,zi)(x_i, y_i, z_i)(xi​,yi​,zi​)，该元素使用随机值 ζ\zetaζ 压缩为 ti=xi+ζyi+ζ2zit_i = x_i + \zeta y_i + \zeta^2 z_iti​=xi​+ζyi​+ζ2zi​。

输入 gate ai,bia_i, b_iai​,bi​ 和输出 gate cic_ici​ 的 gate constraint 扩展如下：

(qLi)ai+(qRi)bi+(qOi)ci+(qMi)aibi+qCi=0,qKi(ai+ζbi+ζ2ci−fi)=0,fi∈{t1,…,tn}.\begin{align} & (q_{L_i})a_i + (q_{R_i})b_i + (q_{O_i})c_i + (q_{M_i})a_ib_i + q_{C_i} = 0, \\ & q_{K_i}(a_i + \zeta b_i + \zeta^2 c_i - f_i) = 0, \\ & f_i \in \{t_1, \dots, t_n\}. \end{align}​(qLi​​)ai​+(qRi​​)bi​+(qOi​​)ci​+(qMi​​)ai​bi​+qCi​​=0,qKi​​(ai​+ζbi​+ζ2ci​−fi​)=0,fi​∈{t1​,…,tn​}.​​

如果第 iii 个 gate 是一个算术 gate，则 qKi=0q_{K_i} = 0qKi​​=0。相反，如果第 iii 个 gate 是一个 lookup gate，则 qKi=1q_{K_i} = 1qKi​​=1。

虽然前两个方程可以通过普通的 PLONK 类似地导出，但第三个方程 fi∈{t1,…,tn}f_i \in \{t_1, \dots, t_n\}fi​∈{t1​,…,tn​} 需要在 plookup↗ 中介绍的专门策略。由于此组件的复杂性，建议查看 plookup↗ 和 PlonKup↗ 论文以获取更多详细信息。

Lookup Arguments（查找参数）

为了理解 PlonKup 的实用性，让我们检查一下为什么 lookup arguments 很重要。如果 ZK 证明系统只允许加法和乘法 gate，那么不能用代数表示的操作简单地需要大量的约束。例如，两个 16 位元素 a,ba, ba,b 的 XOR 在传统 CPU 中是一个轻量级的操作。然而，在 Fp\mathbb{F}_pFp​ 中表示 c=a⊕bcb = a \oplus bc=a⊕b 需要如下的复杂计算： $a_i \cdot (1 - ai) = 0$ 对于 $i \in {1, \dots, 16}$: 16 个 mul 门 $a = \sum{i \in {1, \dots, 16}} 2^{i-1} \cdot a_i$: 15 个 add 门 $b_i \cdot (1 - ai) = 0$ 对于 $i \in {1, \dots, 16}$: 16 个 mul 门 $b = \sum{i \in {1, \dots, 16}} 2^{i-1} \cdot b_i$: 15 个 add 门 $c_i = a_i + b_i - 2a_ibi$ 对于 $i \in {1, \dots, 16}$: 32 个 add 门和 16 个 mul 门 $c = \sum{i \in {1, \dots, 16}} 2^{i-1} \cdot c_i$: 15 个 add 门

\begin{align}
a_i \cdot (1 - a_i) = 0 \textrm{ for } i \in \{1,\dots,16\} : & \textrm{ 16 mul gates} \\
a = \sum_{i \in \{1,\dots,16\}} 2^{i-1} \cdot a_i : & \textrm{ 15 add gates} \\
b_i \cdot (1 - a_i) = 0 \textrm{ for } i \in \{1,\dots,16\} : & \textrm{ 16 mul gates} \\
b = \sum_{i \in \{1,\dots,16\}} 2^{i-1} \cdot b_i : & \textrm{ 15 add gates} \\
c_i = a_i + b_i - 2a_ib_i \textrm{ for } i \in \{1,\dots,16\} : & \textrm{ 32 add gates and 16 mul gates} \\
c = \sum_{i \in \{1,\dots,16\}} 2^{i-1} \cdot c_i : & \textrm{ 15 add gates} \\
\end{align}

这是 48 个乘法门和 77 个加法门。

如果 ZK 证明系统支持 lookup 门，则所需的门数量将大大减少。 首先，将表 TTT 定义为 $T={(x,y,z) \vert x < 2^4, y < 2^4, z = x \oplus y}$，其中包含 $2^8$ 个元素。 然后，XOR 运算可以如下计算：

$a=\sum_{i \in {1,\dots,4}} 16^{i-1} \cdot ai$: 3 个 add 门 $b=\sum{i \in {1,\dots,4}} 16^{i-1} \cdot bi$: 3 个 add 门 $c=\sum{i \in {1,\dots,4}} 16^{i-1} \cdot c_i$: 3 个 add 门 $(a_i, b_i, c_i) \in T$ 对于 $i \in {1,\dots,4}$: 4 个 lookup 门

\begin{align}
a = \sum_{i \in \{1,\dots,4\}} 16^{i-1} \cdot a_i : & \textrm{ 3 add gates}\\
b = \sum_{i \in \{1,\dots,4\}} 16^{i-1} \cdot b_i : & \textrm{ 3 add gates} \\
c = \sum_{i \in \{1,\dots,4\}} 16^{i-1} \cdot c_i : & \textrm{ 3 add gates} \\
(a_i, b_i, c_i) \in T \textrm{ for } i \in \{1,\dots,4\} : & \textrm{ 4 lookup gates}
\end{align}

这只需要 9 个加法门和 4 个 lookup 门。

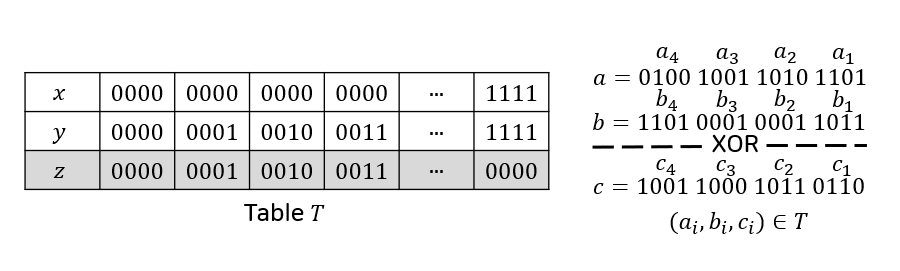使用 lookup 表处理 XOR。

由于 PLONK 中 prover 的复杂度与门的总数成正比，因此一旦启用 lookup 表，XOR 可以更有效地处理。

第一个基于 Lookup 的 ZK 友好哈希函数

很自然地尝试使用 lookup 门来设计 ZK 友好哈希函数。 在 ZK 友好哈希函数中使用 lookup 门的主要优点是它们不是以简单的代数方式表达的，这可以提供对代数攻击的抵抗力。 例如，以代数方式表示条件 $x \in T$ （例如，$f(x) = 0$）需要一个度为 $|T| - 1$ 的多项式 fff。

Reinforced Concrete↗ 是第一个基于 lookup 的 ZK 友好哈希函数，已在 CCS 2022 上展示。Reinforced Concrete 由 Bricks、Concrete 和 Bars 层组成。 其中，lookup 表用在 Bars 层 中。 在 Bars 层中，通过 Bar 函数并行处理 ttt 个元素。 在 Bar 函数中，类似于使用 lookup 门计算 XOR，首先将元素 $x \in \mathbb{F}_p$ 分解为 $(x_1, \dots, xn)$，其中 $x = \sum{i \in {1, \dots, n}} 1024^{i-1} \cdot x_i.$

然后将 $x_i$ 馈送到小型 lookup 表 SSS 中，产生 $y_i = S(xi)$。 然后输出由以下公式决定 $y = \sum{i \in {1, \dots, n}} 1024^{i-1} \cdot y_i,$ 它从 $y_i$ 重构组合输出。

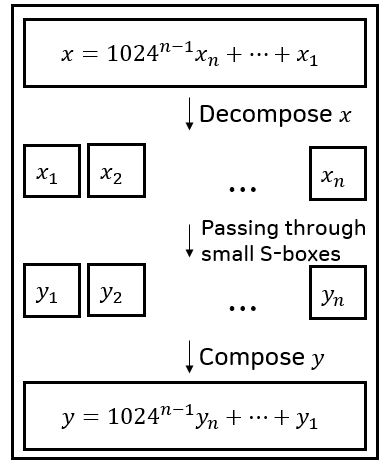Reinforced Concrete 中的 Bar 函数 $bar: \mathbb{F}_p \rightarrow \mathbb{F}_p$。

此结构以规范方式使用 lookup 表，在没有报告已知漏洞的情况下保持合理的效率。 然而，一个关键的缺点是在 ZK 设置中评估 Bars 层的成本很高。 在 Reinforced Concrete 的 15 层中，只有一层是 Bars 层 —— 虽然它仍然占 PlonKup 中约束的 75%。 一般来说，期望且自然的是在多个轮次中迭代一个简单的层。 降低 Bars 层的成本并在多个轮次中迭代它可能会增强安全性，并允许在效率和安全性之间进行权衡。 这激发了 Polocolo 的设计。

Polocolo 简介

Polocolo 是来自不同设计原理的另一个基于 lookup 的 ZK 友好哈希函数。 Polocolo 这个名字来源于 po wer residue for lo wer co st table lo okup。

要将输入 $x \in \mathbb{F}_p$ 映射到 lookup 表，必须通过预处理来约束 xxx 的可能值。 Reinforced Concrete 中的 Bar 函数使用基数扩展方法将 lookup 表应用于 $F_p$ 的元素：$x \in \mathbb{F}_p$ 被分解为 nnn 元组 $(x_1, \dots, xn) \in \mathbb{Z}\{s1} \times \dots \times \mathbb{Z}\{s_n}$，然后每个 $x_i$ 都通过小型 S-box，如前一节所述。 然后，每个组件通过表 lookup 馈送到 S-box 中。 来自 S-box 的输出再次组合以定义 Bar 函数的相应输出。 然而，在大多数 ZK 设置中，基数扩展的成本非常高。

为了解决这个问题，我提出了一种替代方法，称为 power residue 方法，它可以有效地将 lookup 表应用于大素数 p(≈2256) 的 $F_p$ 元素。 Power residue↗ 可以看作是 Legendre 符号的概括。 当正整数 mmm 除以 $p-1$ 时，xxx 的 mmm 次 power residue 定义为 $(\frac{x}{p})_m = x^{(p-1)/m}.$ mmm 次 power residue 采用 m+1 个不同的值，因此每个可能性都可以作为大小为 m+1 的 lookup 表 TTT 的输入。

现在我们新的 S-box $S : \mathbb{F}_p \rightarrow \mathbb{F}_p$ 定义为

$S(x) = x^{-1} \cdot T[(\frac{x}{p})_m].$

通过适当地选择 TTT，可以将此 S-box 制成双射的。 此外，此 S-box 是一个高阶的 S-box，仅需要 14 个 PLONK 门 —— 例如，当 m=1024 时，这明显少于 Reinforced Concrete 的 Bar 函数所需的 94 个门。 使用此 S-box，我提出了 Polocolo，一种新的基于 lookup 的 ZK 友好哈希函数。

在本篇文章的第 2 部分中，我将介绍 Polocolo 的详细规范和密码分析，以及与其他 ZK 友好哈希函数的性能比较。

关于我们

Zellic 专注于保护新兴技术。 我们的安全研究人员发现了最有价值目标中的漏洞，从财富 500 强企业到 DeFi 巨头。

开发人员、创始人和投资者信任我们的安全评估，以便快速、自信且没有关键漏洞地交付产品。 凭借我们在现实世界攻击性安全研究方面的背景，我们发现了其他人遗漏的内容。

联系我们↗ 进行比其他公司更好的审计。 真正的审计，而不是橡皮图章。

• 原文链接： zellic.io/blog/introduci...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～