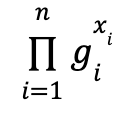17 个关于 SNARKs 的误解（以及为什么会有这样的误解）
- a16z
- 更新于 2024-07-23 16:31
- 阅读 878
17 个关于 SNARKs 的误解（以及为什么会有这样的误解）
SNARKs 是一种重要的密码学工具，为系统设计中的新可能性打开了令人兴奋的大门，尤其是在去中心化环境中，它们可以帮助相互不信任的各方合作和交易。在这篇文章中，我将谈论我在过去几年中看到的技术快速进步带来的一些误解。但首先，让我们快速回顾一下 SNARKs 是什么以及它们在加密货币和其他领域中的重要性。
SNARKs 允许数据由潜在对抗性实体处理，然后证明数据有效且已被正确处理，而无需发布实际数据。例如，Layer2 Rollup 可以向一个不信任的“验证者”（如以太坊区块链）证明他们知道满足某些属性的一些数据，例如一批有效交易，其执行会得到给定的全局状态。这样，以太坊区块链本身无需处理交易，甚至无需存储数据（尽管 Rollup 通常会向区块链发布足够的数据以确保状态可重构）。
如果一个 SNARK 满足所谓的零知识属性，那么它也可以用于隐私保护；例如，让某人证明他们已将资金存入混币池（因此有权从该池中提取资金），而不泄露哪笔存款交易是他们的。实体还可以选择性披露额外信息以符合合规要求，例如他们在白名单上的存在或不在黑名单上，或者他们向指定地址转移适当的税款而不泄露额外敏感信息（例如税款计算的具体细节）。SNARKs 在区块链之外也有许多潜在应用，促进了在其他情况下可能不存在的信任。
SNARKs 起源于上世纪 80 年代和 90 年代，直到最近才从理论转向实践，这得益于研究人员、工程师和 web3 开发人员的进步。我之前讨论过 SNARKs 的设计方式，以及它们的性能和安全性，以及它们的发展历史 。
但随着 SNARKs 的进展加速，以及看到这项技术之美和力量的社区人数增长，重要的是我们在思考和谈论它们时要准确无误。设计空间复杂微妙，导致了各种误解和错误，这减缓了进展并引起了无尽的挫折。我已经整理了一份这些误解的清单，并在这里尝试澄清。我希望这份清单对社区和任何基于 SNARKs 构建的人有所帮助，并欢迎你提出希望我在未来的帖子中解决的其他问题。
术语混淆
1 使用“ZK”表示“简洁”
人们经常使用术语“ZK 证明”来指代并非零知识的简洁论证。同样，ZK-Rollups 通常不使用零知识证明，仅使用简洁证明。
“简洁”意味着证明短小且验证速度快。但“零知识”意味着证明不泄露证明者声称已知的“见证”相关的任何信息。简洁性关乎（验证者的）性能，而零知识关乎证明者敏感数据的隐私。
将“ZK 证明”用于所有简洁论证的做法可能始于第一个大规模部署 SNARKs 的项目 ZCash，因为该项目实际上是零知识的，因此该术语在指代该特定项目时是准确的。也可能是人们简单地没有一个简短的术语来表示“简洁论证”，并开始使用 ZK，尽管这并不准确（“基于 SNARK 的 Rollup”不像“ZK-Rollup”那样有趣且易于说）。
作为一个社区，我们应该更加准确。虽然技术专家可能能够解析预期的含义，但我经常与对此完全困惑的人交谈，尤其是因为“ZK”确实有一个精确的技术含义。
这不仅仅是迂腐的。期望每个人以某种方式区分术语的准确使用和不准确使用存在真正的风险。某人可能会认为一个 SNARK 库满足零知识，因为它将自己标记为“ZK” - 即使它泄露了有关见证的信息 - 这会导致他们在隐私关键应用中危险地部署一个非零知识库。
建议： 我发现用“可验证 Rollup”或“有效性 Rollup”代替“ZK-Rollup”更直观。当我想引用简洁论证（可能是零知识也可能不是）时，我会说 SNARK 或“简洁论证”，而不是 ZK 证明。在需要强调 SNARK 是零知识的情况下，我会说“zkSNARK”。
2 “简洁”术语的变体
SNARK 中的“S”代表“简洁”，广义上指的是具有短证明和快速验证的证明系统。尽管这似乎很简单，但人们在使用“简洁”一词时在数量上指的是不同的事物，导致混淆。
许多作者使用术语“简洁”来指代证明长度和验证时间最多为见证检查过程运行时间的对数多项式。其他人甚至将其仅用于指代常数大小的证明。然而，我将其用于指代次线性而不是对数多项式或常数。
我认为其他人应该采用这种做法：首先，正确的“简洁”定义应该涵盖任何具有定性验证成本的协议 - 我指的是证明者向验证者发送整个见证，验证者直接检查其正确性的系统。此外，一旦设计了具有定性验证成本的证明系统（例如 $$ \sqrt {nλ} $$ 哈希），通过 SNARK 组合，可以进一步降低成本而无需显著增加证明者时间。
其次，优越的渐近性并不总是转化为优越的具体性能。（例如，参见第 16 条中 Ligero 和 FRI 多项式承诺的比较。）
如果我们坚持认为证明系统具有对数多项式验证成本才能被视为 SNARK，那么我们必须使用完全不同的术语来指代使用 Ligero 多项式承诺（其验证执行大约 $$ \sqrt {nλ} $$ 哈希）而不是 FRI（其验证执行大约 $$ λ log(n)^2 $$ 哈希）的项目。这将是不好的：由此产生的协议具有相同的安全属性，而且 FRI 的证明大小优势甚至在某些应用中实际产生的陈述(statements)比那些实际产生的陈述更大时也不会发挥作用（而 Ligero 的证明优势在所有大小上都存在）。要更加精确和包容，我使用“简洁”来指代任何具有次线性证明大小的协议，“省力(work-saving)”指代任何具有次线性验证时间的协议。这确保了具有小证明但线性时间验证的 SNARKs（例如基于 IPA / Bulletproofs多项式承诺方案的 SNARKs）确实符合 SNARKs 的定义。
为什么许多作者将对数验证成本作为“简洁”的标准？这种做法源于在理论背景下，对数成本被视为一个自然的界限，类似于“多项式时间”被视为理论计算机科学中“高效”算法的基准（尽管许多多项式时间算法是不切实际的）。
但是，SNARK 设计与多项式时间算法的研究相比更少，而与次线性算法领域更为接近，后者研究如何处理数据量很大的输入，以至于算法无法读取或存储整个输入。与今天对 SNARKs 的研究一样，次线性算法受到实际考量的推动。就像在次线性算法中总是存在一个显而易见的线性成本解决方案（即读取和存储整个输入），在 SNARKs 中总是存在一个显而易见的证明系统（即证明者向验证者发送整个见证）。
因此，就像次线性算法领域选择包容一样——宣称任何具有次线性成本的解决方案都是有趣的——我们应该对 SNARKs 采取同样的态度。
3 SNARKs vs. STARKs
我经常被要求解释 SNARKs 和 STARKs 之间的区别，以至于我不得不在这里讨论它们的含义。
SNARK代表简洁的非交互式知识证明（Succinct Non-interactive ARgument of Knowledge）。我已经解释了“简洁（Succinct）”的含义。“非交互式”意味着验证者不必向证明者发送任何挑战，因此证明可以（例如）被发布在区块链上，以便任何区块链节点可以在方便时验证。 “知识论证（ARgument of Knowledge）”意味着，唯一的方法是，多项式时间的证明者可以找到一个令人信服的证明，即其确实知道见证（witness）。
STARK在科学文献中被引入具有精确的技术含义。它代表可扩展的透明知识证明 Scalable Transparent ARgument of Knowledge. 。(很多人都认为S的意思是“简洁”，就像它在SNARK中的意思一样;参见本文的3.3节)。但是在这里， S 是“可扩展（Scalable）” 但是在这里，“可扩展”意味着证明的（prover）时间最多是准线性的（即在证明的过程中是线性的，到接近对数），并且验证成本（时间和证明大小）最多是在这个运行时的对数级别。 “透明”意味着证明系统不需要可信设置 。根据这个技术定义，今天存在许多 STARKs。
那么造成混淆的原因及其后果是什么？至少有三个。
首先，在公共讨论中，“STARK”的含义，就像“ZK”一词一样，已经大大偏离了我上面解释的技术含义。该术语现在通常用于指代 StarkWare 的证明系统（将 Stark 纳入其品牌名称）及其密切衍生物。
这里的一个重要澄清是，“STARK”一词并未指定协议是否交互式。据我所知，今天的 STARKs 都是以非交互方式部署的（这使它们成为了 SNARKs）。这在公开讨论中对于已部署的证明系统的安全性造成了重大混淆。
其次，当部署交互式证明系统时，可能适用的安全级别要低得多，而不像部署非交互式证明系统时那样。攻击交互式部署的攻击者在不与验证者交互的情况下无法知道攻击是否会成功，这极大地降低了速度，增加了尝试攻击的成本，并使攻击对验证者来说是显而易见的。此外，相对于交互式部署，非交互式部署背后的加密假设更强 。
由于“STARK”一词并未指定协议是否交互式，这使得任何关于部署的安全参数的讨论都变得混乱。在我之前发表的关于这个主题的博客文章后，多人联系我告诉我，他们认为当前的 STARKs 部署是交互式的，因此适用较低的安全级别。他们是错误的。
第三，引入“STARK”一词导致许多社区滥用“SNARK”一词，错误地将其用于指代具有可信设置的 SNARKs，例如 Groth16 及其前身。这是为了区分那些 SNARKs 与 StarkWare 及其后代。
建议： 我们不需要为协议可能满足的每个属性集合使用不同的首字母缩略词，特别是如果这会导致关于适当安全级别等核心问题的混淆。术语“透明（transparent） SNARK”非常清晰，应该用来指代任何透明 SNARK。如果交互式类似物被部署，它可以简单地被称为透明交互式证明。（在本文中，我使用“STARK”一词来指代 StarkWare 及其派生物的证明系统，因为这里描述的一些误解特指这些证明系统。）
一些关于 SNARKs 设计者和用户的常见误解
4 只有 Plonk 后端可以支持“Plonkish 电路”，只有基于 STARK 的后端可以支持 AIR
今天许多项目使用了过于针对特定后端的约束系统类别。因此，人们经常无法区分约束系统本身和它们专门针对的后端。此外，社区直到现在仍未意识到，与这些约束系统专门针对的后端不同的后端仍然可以证明关于它们的陈述（并且还能获得性能优势）。
这些误解导致了在科学文献和公共讨论中对不同后端相对性能的不正确断言。结果部署了性能不佳的 SNARKs。
背景
- SNARKs 通常是通过首先应用前端来部署的，前端将适当的见证检查过程（witness-checking procedure）转换为一种电路；然后应用后端，即电路可满足性的 SNARK。
- “Plonkish”指的是 Plonk 后端可以证明的一种电路（或者更准确地说，约束系统）。
- 代数中间表示（AIR：Algebraic Intermediate Representation ）指的是另一种电路（大致上是一种特定结构的 Plonkish 电路），其是 STARK 后端可以证明的电路。一个常见的误解是 Plonk 是唯一能够证明关于 Plonkish 电路的陈述的后端，STARKs 是唯一能够证明关于 AIR 的后端。实际上，人们经常未能区分“Plonkish”（这是一种约束系统）和 Plonk（一种特定的后端，可以证明关于 Plonkish 约束系统的陈述）。我也遇到了类似的未能区分 AIR 和 STARK 后端的情况。
这种混淆是可以理解的。事实上，除了令人困惑的命名惯例外，关于 Plonkish 和 AIR 的定义通常针对 Plonk 和 STARK 后端的工作方式的低级细节进行了调整。
实际情况是什么: 大多数 SNARKs 可以很容易地进行调整，以支持 Plonkish 和 AIR。
主要的例外是 Groth16 及其前身，它们仅限于“二次约束（degree-2 constraints）”并且在特定情况下实现了最快的验证，特别是对于称为“rank-one 约束”（R1CS）的二次约束系统的一个子类。（顺便说一句，许多人没有意识到 Groth16 及其前身可以修改以支持任意的二次约束，而不仅仅是 rank-one。验证者的成本随着约束的等级增加而增加，但可以通过递归降低。请参见下面的 #6。）
一些人似乎对各种 SNARKs 的相对通用性有本质上的倒退的概念。Plonk 及其后代如 Hyperplonk 在没有证明者产生额外开销无法处理 R1CS 。但是，诸如 Spartan 和Marlin这样的 SNARKs - 最初被描述为针对 R1CS 的，通常被认为不支持像 Plonkish 和 AIR 这样的流行电路类别，但其实可以支持。
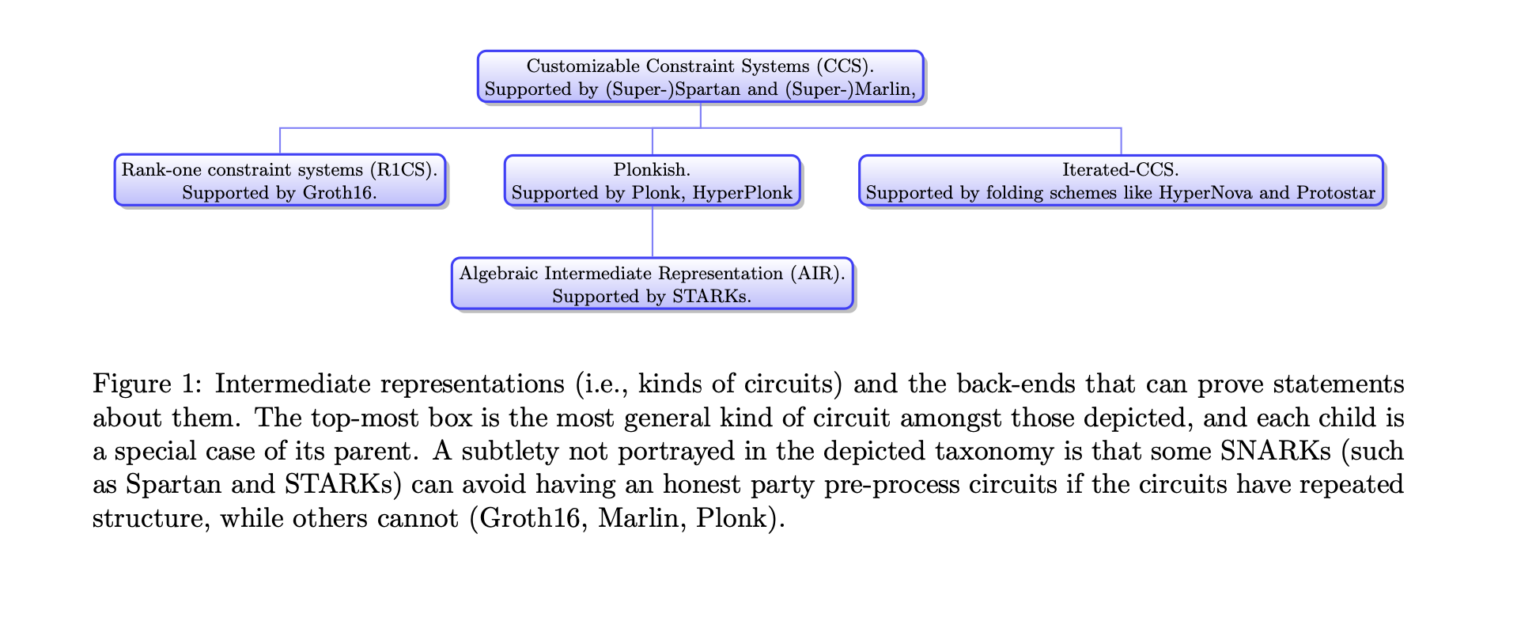
事实上，Spartan 和 Marlin 支持 R1CS、Plonkish 和 AIR 的一个清晰的泛化称为可定制约束系统 （CCS）（见下面的图 1）。它们可以带来性能优势。例如，Plonk 要求证明者承诺电路中每个“线（wire）”的值，并使用所谓的复制约束来确保分配给每个从单个门出来的 wire 的值相等。这些承诺成本通常是证明者的瓶颈。因此，使用 Plonk 及其变体的工程师们致力于开发诸如“相对引用”之类的概念，目的是在 Plonkish 电路中最小化复制约束 。
在 Spartan 中，当处理具有重复结构的电路时，证明者仅对电路中每个乘法门承诺一个值。门总是比线少（通常至少是 2 的倍数）。当 Spartan 应用于具有重复结构的电路时，加法门“免费”：加法门不会增加证明者的承诺成本，也不会增加证明者的其他成本，除了增加“直接见证检查”所需的工作量，即在没有正确性保证的情况下评估电路所需的工作量。
尽管它们很受欢迎，AIR 和 Plonkish 电路的概念过于受到 Plonk 和 STARK 后端的低级细节的影响。在这种情况下，模块化（在这里的意思是清晰地将用于表示见证检查过程的电路类型与用于证明该电路的可满足性的后端分开）具有概念上和性能上的好处。
建议：我主张使用像 CCS 这样的约束系统，它与 R1CS 的定义方式相同，仅涉及矩阵-向量乘积和 Hadamard（即逐元素）向量乘积。正如 R1CS 与用于证明它的 Groth16 等流行后端明显不同一样，CCS 与用于证明与之相关的任何特定后端也是明显分开的。CCS 可以在不增加额外开销的情况下捕捉到当今实践中使用的所有最流行的约束系统。
5 针对 R1CS 的 SNARKs 无法支持lookup 论证
背景： lookup 论证 是一种专门的 SNARK，可以与通用 SNARK 结合使用，大大减少通用 SNARK 摄入的电路的大小。在 SNARK 设计中，lookup 论证的概念是在 Arya 中引入的，该文描述了它们在 fan-in 2 的算术电路的背景下，即 R1CS 的一个特殊情况。
鉴于此，我不知道关于针对 R1CS 的 SNARKs 无法与lookup 论证进行对接的误解是如何产生的。也许这与 Plookup 有关，这是一种流行的 lookup 论证，最初是使用受 Plonk 后端启发的技术呈现的。但类似于 Plonk 不是唯一支持“Plonkish 电路”的后端一样，Plonk 也不是唯一能够证明 Plookup 隐含的约束系统的后端。
许多lookup 论证归结为“大乘积（grand product）”参数 - 计算大量承诺值的乘积。大乘积可以通过扇入 ( fan-in) 2 的算术电路高效计算（通过乘法门的二进制树），这是 R1CS 的一个非常特殊的情况。在计算大乘积时，人们可能不希望将 R1CS 的 SNARK 作为黑匣子使用，而是修改 R1CS 的 SNARK 的基础技术以利用大乘积的特殊结构，以提具体效率（例如，参见 这个论文 的第 5 和第 6 节）。
影响： 这种误解导致了对不同 SNARKs 的相对性能的公开估计中存在重大错误。一个典型的错误是在比原本描述为针对 R1CS 的 SNARKs 所需的电路要大一个数量级以上的电路上运行这些 SNARKs，理由是前者无法支持lookup 或高阶约束。然后实验者自然地得出结论，即后者比前者更快。但他们之所以得出这个结论，仅仅是因为前者在一个比必要更大的电路上运行。
一个相关（但更普遍）的错误是将一个后端与多项式承诺方案 和大的证明（大小）结合起来，然后得出结论说后端本质上具有大证明。实际上，证明大小主要由具体的多项式承诺方案的选择确定。在很大程度上，任何 SNARK 都可以使用任何多项式承诺方案，主要的复杂性在于一些 SNARKs 需要对多线性多项式进行承诺，而另一些则需要对单变量多项式进行承诺。
建议： 理解哪些前端技术（以及其他优化）可以与哪些后端结合使用可能具有挑战性。因此，SNARK 设计者对于不同后端的相对性能往往得出不准确的结论。
一些混淆是不可避免的，因为新的前端技术（以及其他优化）通常在特定后端的背景下描述，尽管它们更普遍适用。此外，现有的后端可能需要修改以与新的前端和其他优化进行对接。但我们可以并且应该改善这种现状。例如，社区可以鼓励对最初被描述为针对 R1CS 的后端更深入理解，直到现在一直被诟病为无法与某些前端技术对接。我们可以鼓励人们在断言无法与新前端或其他优化对接之前，更加认真地努力修改现有的后端。最后，尽可能使用相同的多项式承诺方案比较不同的后端。
6 Plonk 对于证明来说比 Groth16 更快
背景： Groth16 需要一个特定于电路的可信设置；证明新电路的可满足性需要运行一个新的可信设置。Plonk 具有通用设置，意味着一个设置支持所有直到指定大小限制的电路。人们可能会认为 Plonk 证明应该为实现通用设置而付出性能代价，然而许多人认为 Plonk 证明实际上比 Groth16 证明更快。
事实更加微妙。
细节： Plonk 无法支持 R1CS 而不带有额外开销。Groth16 针对 R1CS，但无法支持 Plonkish 电路。因此，它们支持的电路类型是无法比较的。但两者都支持具有两个输入的加法和乘法门的电路，当应用于这样的电路时，Groth16 实际上比 Plonk 更快。
具体来说，Plonk 要求证明者执行 11 次多标量乘法（MSM），每次的长度等于电路中门的数量，即乘法门和加法门。
Groth16 只需要在群 $$ G_1$$ 上进行 3 次 MSM，以及在 $$ G_2$$ 上进行 1 次 MSM（其中$$ G_1$$ 和 $$ G_2$$ 是具备配对的群）。此外，对于 Groth16，这些 MSM 中的每一个仅与乘法门的数量相等（在 Groth16 中，加法门是“免费”的）。在 $$ G_2$$ 上的 MSM 大约比在 $$ G_1 $$ 上的慢 2 到 3 倍，因此这相当于在 $$ G_1 $$ 上进行 5 到 6 次 MSM，每次的大小等于乘法门的数量。这可能比 Plonk 证明的工作快很多，这取决于加法门的数量。
许多人认为 Plonk 比 Groth16 更快，因为对于一些重要应用，Plonkish 电路可以比捕捉相同应用的 R1CS 实例要小得多（例如 MinRoot 和Pedersen hashing）。但要利用这一点，需要有时间和专业知识编写经过优化的 Plonkish 电路（除非当然，其他人已经完成了这项工作）。这项工作通常是手工完成的，尽管未来的编译器可能能够自动利用 Plonkish 电路的全部表达能力。如今的做法是耗时且困难的（指定 Plonkish 约束系统中的任何错误都会破坏系统的安全性）。
此外，正如上文第 5 点中提到的，许多人并不意识到 Groth16 及其前身可以修改以支持任意二次约束，而不仅仅是R1 约束。（非 R1 的约束有时被称为自定义约束。）Groth16 的限制在于无法超越二次约束，而不是缺乏对自定义约束的支持。（另一个鲜为人知的事实是 Groth16 的前身，如 Zaatar，可以处理高次约束，但它们产生两轮、隐私硬币的论证，因此不允许链上验证。）
要点: Plonk 可以比 Groth16 产生更快的证明 - 但并非总是如此。即使可以，要实现这一点通常需要开发人员投入相当的专业知识和时间。
7. STARKs 依赖的假设比椭圆曲线密码学的替代方案更少或更弱
STARKs 中唯一使用的密码学原语是加密哈希函数。基于椭圆曲线密码学（ECC）的 SNARKs 假设在某些椭圆曲线群中解离散对数问题是困难的（可能还有其他假设）。
如果 FRI 在随机预言模型中的参数下被证明达到目标安全级别，我会同意这种说法的精神，但事实并非如此。今天基于 FRI 的 SNARKs 广泛部署在未经证实的猜想下，即已知对 FRI 的攻击恰好是最优的。这是为了控制证明大小和验证成本。（有关猜想的详细信息，请参考我的先前帖子 ，有关其性能影响，请参阅下文第 9 点。）
在这里，FRI 是 STARKs 底层的流行多项式承诺方案，当应用于度为_n_的多项式时，其证明包含 $$ O(λ log(n)^2)$$ 次哈希评估，其中λ是安全位数 。更准确地说，FRI 是一种测试承诺函数是否为低次的方法（请参阅这个讲座以获取我对此的最佳阐述），它可以用于提供多项式承诺方案（请参阅前述讲座的第 59-65 页）。
总之，虽然可以在保守的安全假设下部署 STARKs，但现有项目并未这样做。
8 假设相同多项式承诺方案或 SNARK 的部署具有类似的运行时间
对于多项式承诺方案，参数选择可以显著影响证明者运行时间和证明大小，特别是对于仅使用哈希的方案（例如 FRI、Ligero、Brakedown 等）。
在来自这一类部署的 SNARKs 中， 域(field)大小和称为膨胀因子（blowup factor）$B$ 存在重大差异，膨胀因子$B$控制着证明者时间和证明大小之间的权衡。证明时间与 $B$ 成线性关系，而证明大小与 $1/log(B)$ 成线性关系。例如，膨胀因子为 16 可能导致比膨胀因子为 2 小 4 倍的证明，但会使证明慢 8 倍。
一些项目将基于 FRI 的 SNARK 与基于椭圆曲线的 SNARK 组合，以在上链前缩小 FRI 证明大小。这些项目可以配置 FRI 证明者更快，证明更大，因为 FRI 证明不会直接上链。其他项目直接将 FRI 证明上链，因此配置证明者会慢得多。
具体来说，如果在 251 位域上使用膨胀因子为 16 运行 FRI，对于给定的多项式度限制，证明者可能比使用膨胀因子为 4 和（扩展的）64 位域时慢 10 倍以上。在这种比较中，4 倍来自于 4 倍的膨胀因子，其余来自于更大的域（因为更大的域使 FFT 和 Merkle 哈希比 4 倍慢）。
9. 将 FRI 和 STARK 证明描述为几十 KB
这是对 FRI 和 STARK 的证明长度的标准描述。但事实上，即使在上文第 7 点讨论的猜想下，FRI 证明在 100 多位安全性下实际上是多达数百 KB。
例如，使用膨胀因子为 4，将最简单的 FRI 实现应用于 128 位安全性下的 $2^{20}$ 次多项式，会导致证明大小接近 500 KiB。通过某些优化（如“grinding”、“Merkle-capping”和“early stopping”），可以将证明大小降低，但这些技术不会将证明大小降至 200 KiB 以下。“几十 KB”的描述似乎指的是我之前在博客文章中讨论的 FRI 的配置。该配置针对 80 位安全性，根据激进的假设，其中 32 位来自grinding技术，只有 48 位来自 FRI 本身。此外，该配置使用了一个大的膨胀因子 16，导致证明速度较慢。在该博客文章中讨论的 SHARP 验证器随后已更改为更高安全性的配置，但 StarkEx dYdX 验证器今天仍保持在博文中讨论的配置中。
将 80 位增加到 128 位会使证明大小翻倍。将膨胀因子从 16 减少到 4 以获得更合理的证明时间会再次使证明大小翻倍。去除在上述第 7 点中讨论的激进安全假设会再次使证明大小翻倍（至少）。将由grinding贡献的安全位数从 32 降低到 16（因为使用grinding获得 32 位安全性会强迫诚实的证明者执行 $2^{32}$ 次哈希）会使证明大小再增加 33%。
这些增加使得几十 KB 和几百 KB 之间产生了差异。
研究人员和 SNARK 设计者的误解
10. 将群指数化混淆为群乘法
背景： 在一个乘法群中，一个群操作（ group operation）接受两个群元素 $g_1$、$g_2$ 作为输入，并输出它们的（群）乘积 $g_1 * g_2$。群指数化是指将某个群元素 $g$ 提升到某个幂$x$。也就是说，指数化计算给定$g$和指数$x$作为输入时的值 $g^x$。
一般来说，指数 $x$ 可以是群的大小 $|G|$ 之间的任意数字。通过标准的平方-乘法算法计算指数化所需的总群操作（即乘法）数量约为 $3/2 log |G| $. 密码学群的大小至少约为 $2^{256}$。因此，群指数化的速度大约是群操作的 400 倍(慢)。
然而，许多关于 SNARK 的论文将群指数化称为群操作。如果我们不区分证明者运行时间中 400 倍因素，我们就无法清楚地了解 SNARK 性能。
建议： 我不确定这里的潜在问题是粗心的计算还是对这些操作具有实质性不同成本（无论是渐近还是具体）的意识不足。然而，我怀疑是后者：很难想象协议设计者会故意忽略这么大的成本差异。
我们需要增加对这些操作实际成本的认识，并鼓励在论文和演示中进行更精确的成本核算。更加强调实施，以及更加谨慎的基准测试，也将是有帮助的。
11 将多次指数化与多指数化（也称为 MSM）混淆
背景: 大小为 $n$ 的多指数化(multi-exponentiation)计算以下形式的表达式
也就是说，多指数化操作输出 $n$ 个指数化结果的乘积。根据加法群符号，这也经常被称为 MSM（多标量乘法）。
朴素地计算多指数化意味着独立执行每个指数化（每个的成本为 $ 3/2 log |G| $ 群操作），然后将结果相乘。然而，Pippenger 的著名算法计算多指数化的群操作数量比这种朴素算法少大约 $log n$（请参见本文第 4 节，其中有一个很好的阐述）。如果 $n$ 是几百万或更大，这种“Pippenger 加速”在实践中很容易达到 20 倍或更多。
许多论文未能区分群操作和指数化，也未能区分 $n$ 次指数化和大小为 $n$ 的多指数化，导致对具体性能成本的额外不精确。
建议. 与 #10 一样，解决方法是提高对这些操作实际成本的认识，更精确的成本核算，以及更加关注实施和基准测试。
12 将安全参数λ视为常数
如果攻击者必须执行约 2λ的工作才能找到一个具有接近 1 的概率的虚假陈述的令人信服的证明，则 SNARK 具有λ位的安全性。
从渐近的角度来看，安全参数必须对输入大小超对数级别，以确保安全性能对超多项式时间的对手。也就是说，λ应被视为大于任何对数因子。
在具体情况下，λ应该是 128 及以上。对于实际输入大小 $n$ ，这比 $log(n)$ 大 3 到 6 倍。在实践中，可以将λ视为约为 $4*log(n)$，但不要忘记 4 这个因子。
在 SNARK 中用λ因子替换 $log(n)$ 因子会使 SNARK 变得更昂贵而不是更便宜，无论是具体上还是渐近上。
13 认为 Fiat-Shamir 转换通常不会导致安全性的重大损失，除非应用于“基础协议”的顺序重复
误解: 下面涉及顺序重复的示例揭示了将 Fiat-Shamir 应用于一个 $r$ 轮交互协议可能导致安全位数损失 $r$ 倍。许多人认为，顺序重复是产生这种损失的交互协议的主要自然技术。实际上，还有其他情况。
背景和示例: 对具有失真错误½（即“1 位交互安全性”）的一轮交互协议进行λ次顺序重复，可以获得一个具有失真错误 $2^{-λ}$（即“λ位交互安全性”）的λ轮交互协议。将 Fiat-Shamir 转换应用于这个λ轮协议可能导致完全不安全的结果：所谓的 grinding 攻击可以通过大约λ个哈希评估找到任何虚假陈述的令人信服的证明（即经过 Fiat-Shamir 处理的协议只有 log(λ)位安全性）。
在对 Fiat-Shamir 处理的协议进行攻击时，作弊的证明者会分别攻击每一轮。首先，它在第一次重复中对证明者消息进行穷举(grinding)，直到找到一个哈希到“幸运”验证者响应的消息。从期望值上看，这只需要尝试 2 次证明者消息（因为失真错误 ½意味着任何特定的证明者消息以½的概率产生幸运的验证者响应，因此尝试两个消息后，证明者期望找到一个幸运的消息）。
一旦找到这样一个证明者消息 $m_1$，它就完成了对第一次重复的攻击。它固定第一轮消息为 $m_1$，并继续对第二次重复的证明者消息进行穷举(grinding) ，直到找到一个哈希到幸运验证者响应的消息。同样，在期望值上，这只需要 2 个哈希 - 依此类推，直到所有重复都成功攻击为止。
现实: 平行重复与 Fiat-Shamir 相结合也可能导致严重的安全风险。（攻击首次由 Attema, Fehr, and Klooß 提出。）
例如，假设你采用一个具有 64 位交互安全性的 2 轮基础协议（即，验证者向证明者发送两条消息），并在并行中重复两次，获得一个具有 128 位交互安全性的两轮协议。为了说服验证者在两次重复中都接受，证明者必须在两次重复中都幸运，这发生的概率为 $2^{-64} * 2^{-64} = 2^{-128}$。然后，如果你应用 Fiat-Shamir 使协议非交互式，它的安全性最多为 64 位，基本上与你根本没有重复基础协议时相同。
对 Fiat-Shamir 化的协议的攻击再次一次攻击一次重复。攻击者在第一条消息 m1 上进行穷举(grinding)，直到在两次重复中的一次中获得幸运的验证者挑战。（通过“幸运”，我们指的是攻击者可以轻松通过该特定重复的基础协议中验证者的所有检查。）预期需要最多 264 个哈希评估，然后攻击者找到这样的消息 m1。固定 m1，然后攻击者在另一次重复的第 2 轮中的消息 m2 上进行穷举(grinding)，直到获得幸运的验证者挑战。在找到幸运消息之前，大约需要 264 个哈希评估。此时，攻击者已经破坏了基础协议的两次重复。
建议: 结论是，如果希望将 Fiat-Shamir 转换应用于具有多轮的交互式协议，那么为了排除重大安全风险，确实应该表明该交互式协议满足一种被称为逐轮可靠性的加强版本。逐轮可靠性交互式协议 - 即使它们有许多轮 - 在随机预言者模型中应用 Fiat-Shamir 转换时不会失去安全性。一个这样的例子是 sum-check 协议（请参阅本文第 2.1 节）。IPA/Bulletproofs是另一个在随机预言者模型中应用 Fiat-Shamir 后已知安全的多轮协议。
令人惊讶的是，FRI 是一个对数轮协议，直到现在还没有被证明是逐轮可靠性 - 尽管我所知道的所有部署都应用 Fiat-Shamir 使其非交互式，并且多篇 研究 论文已经声明了关于 FRI 逐轮可靠的安全性保证。因此，与许多先前的断言相反，基于 FRI 的 SNARK 并不被认为在随机预言者模型中是安全的。幸运的是， 新工作解决了现有安全分析中的这一差距。这并没有解决这些部署所依赖的关于 FRI 可靠性的额外猜测（请参见上面的 #7）。
奖励：要避免的相关安全陷阱。 当我们讨论应用 Fiat-Shamir 转换的危险时，请记住对要证明的陈述的任何输入（或参数）进行哈希处理，这些输入可能受到对手的控制。
如果未这样做，攻击者可以生成一个通过验证者的所有检查的 SNARK 证明，除了最后一个检查外，然后轻松找到一个使甚至这个最终检查通过的输入。多年来，这种漏洞已经多次在使用 Fiat-Shamir 转换的协议部署中出现 。这个问题很常见，我们有术语来指代它：“弱 Fiat-Shamir”。
使用弱 Fiat-Shamir 漏洞，攻击者可以找到虚假陈述并说服证明其真实性，但无法完全控制它所找到的虚假陈述。也就是说，对手不能随意选择一个虚假陈述，然后找到一个令人信服的证明π。尽管如此，这种漏洞的影响可能是毁灭性的，正如上述作品所探讨的。
14 更高性能 SNARKs 的关键是在越来越小的域上工作
已经有很多出色的工作致力于设计在小域上工作的 SNARKs - 特别是比椭圆曲线群使用的域（通常为 $2^{256}$ 或更大）小的域。这里的动机是，小域中的域操作（例如，大小为 $2^{64}-2^{32}+1$ 的域）可以比大域中的相同域操作快得多。此外，一些硬件，如 GPU，本身就是在 32 位数据类型上进行操作，使得在非常小的域上进行操作特别快。
我看到的公开讨论在这个问题上忽略了一个重要的细微差别：即使有选择小域的选项，是否使用小域是高度应用相关的。例如，rollup 服务器的主要任务之一是证明对 ECDSA 数字签名的知识。这些是关于大域的陈述。在小域上工作实际上会增加证明 ECDSA 签名知识时的时间。用于数字签名验证所需的每个大域操作都必须通过 SNARK 所在的小域上的许多操作来模拟。
对于预 zkEVM rollups，证明数字签名的知识是证明者的瓶颈。例如，这可能是为什么 Starkware 使用与某些 ECDSA 签名匹配的 251 位域 ，而不是更小的域。 （EVM 涉及足够复杂的逻辑，例如 Merkle-Patricia trie 更新，证明签名的知识可能不是 zkEVM 的瓶颈。）
另一个例子，EVM 使用 256 位字作为其字大小。如果在小于 $2^{256}$ 的域上工作，则必须分配多个域元素来表示单个 uint256 数据类型。当使用接近 2 的幂的域大小时（例如 Goldilocks 域）时，这尤其痛苦。例如，251 位域“稍微小了一点”以表示 uint256 数据类型。这大致使支持这些数据类型所需的证明成本翻倍。
我的想法: 大域也是一个潜在可以利用的资源，可以利用单个大域操作模拟许多小域操作。我期待在不久的将来看到更多关于这方面的进展。与此同时，在小域上工作是一个很好的选择。但在所有情况下，这并不是更快 SNARKs 的关键。
15. 内积论证需要线性验证时间
内积论证(Inner product)是多项式承诺的一种泛化：它允许一个不受信任的证明者揭示与验证者指定的任何其他向量的承诺向量的内积。今天最知名的内积论证是 IPA/Bulletproofs，它具有线性时间验证。许多项目优先考虑次线性验证，因此忽略了内积论证。著名的例外包括ZCash Orchard 协议和 Monero，因为 IPA/Bulletproofs 的验证时间对于这些应用程序来说已经足够快 。虽然 IPA/Bulletproofs 具有线性时间的验证，但这并不是故事的终点。例如，Dory 是一种透明且同态的内积论证，具有对数验证时间和证明大小（尽管证明大小在具体情况下比 IPA/Bulletproofs 大一个数量级）。此外，与所有同态承诺一样，IPA/Bulletproofs 具有吸引人的批处理特性，在可以分摊的情况下，使其验证在时间上是次线性的。
还有其他透明的多项式承诺，直接受到内积论证工作线的启发，具有极具前景的成本概况。一个例子是 Hyrax，它的证明者非常快，但今天并不流行，因为它的证明很大（与承诺多项式的大小成平方根）。然而，通过 SNARK 组合可以减小证明大小。
16. FRI 证明比具有相同安全性质的其他协议的证明更小
现实情况: 这取决于被承诺的多项式的次数。对于次数高达约 $2^18$ 的多项式，FRI 证明实际上比一种名为 Ligero 的替代方案要大。这是在不将 Ligero 的安全性基于任何关于统计安全性的未经证实的猜想的情况下成立的，同时将 FRI 的安全性基于这些猜想（参见上面的＃7）。
$2^18$ 次数确实比大多数项目今天使用的要低。但一些项目计划在未来使用这个次数的多项式，以控制 FRI 证明者的巨大内存成本（多达数 GB）。
如果不将 FRI 的安全性基于上述 #7 中提到的猜想，则直到次数大约大于 $2^20$ 时，Ligero 证明仍然比 FRI 证明小。（更详细的比较可以在这里找到。）
总之，不同证明系统的渐近比较在实例大小大于实践中出现的大小之前不一定匹配其具体成本。将 FRI 应用于次数小于 $2^20$ 的多项式的项目应考虑切换到 Ligero 以获得改进的性能并避免强安全性猜想。
17 SNARKs 今天的性能足够好，应该现在固化
Justin Thaler是 a16z 的研究合伙人，也是乔治城大学计算机科学系的副教授。他的研究兴趣包括可验证计算、复杂性理论以及大规模数据集的算法。
