现代 DeFi: 最小化借贷协议 Morpho
- WongSSH
- 发布于 2023-11-30 17:59
- 阅读 5021
概述Morpho是目前以太坊内第四大借贷协议(数据来源为defillama)。相比于其他高度复杂的借贷协议,MorphoBlue的合约使用了500行代码就完成了所有的借贷工作。同时,Morpho也是一个无许可的借贷协议
概述
Morpho 是目前以太坊内第四大借贷协议(数据来源为 defillama)。相比于其他高度复杂的借贷协议,Morpho Blue 的合约使用了 500 行代码就完成了所有的借贷工作。同时,Morpho 也是一个无许可的借贷协议,任何用户都可以调用合约内部的 createMarket 函数使用指定的参数创建交易市场。但是需要注意,Morpho 也并不是完全自由的,用户不可以随意指定一些借贷参数。
清算规则和利率
总所周知,在一个借贷协议内最终部分永远是利率计算和清算部分。我们首先介绍清算部分。对于清算,Morpho 也使用了传统的 LTV 方案。我们可以使用以下公式计算某一个仓位的 LTV: $$ LTV = \frac{\text{BORROWED AMOUNT} ∗ \text{ORACLE PRICE}}{\text{COLLATERAL AMOUNT} * \text{ORACLE PRICE SCALE}} $$ 上述公式内的参数含义如下:
BORROWED AMOUNT用户借出的资产的数量ORACLE PRICE借出资产的预言机价格COLLATERAL AMOUNT抵押品的数量ORACLE PRICE SCALE一个常数,其数值为1e36
有读者一定会好奇,这里为什么没有出现抵押品价格的信息。这是因为 Morpho 和大部分现代借贷协议一样采用了相对价格预言机,即预言机返回的价格是一个比价情况。比如用户使用 DAI 作为抵押品借出 USDT 。那么此处的 ORACLE PRICE = USDT / DAI。我们会在本文内介绍如何实现一个基于 Chainlink 的预言机。
在使用 LTV 的借贷系统内,往往存在一个最大值,当 LTV 大于某一个阈值时,用户的资产就会被清算。换言之,即用户借出的资产大于抵押资产的某一个比值时就会被清算。在 Morpho 的文档内,我们称这个 LTV 的阈值为 LLTV。Morpho 不允许用户设置任意的 LLTV。目前支持 [0%; 38.5%; 62.5%; 77.0%; 86.0%; 91.5%; 94.5%; 96.5%; 98%] 档次。假如读者有部署 Morpho 目标,请参考 最新文档。更加权威的方法应该是在 Dune 内使用以下 SQL 代码检索:
SELECT
lltv / 1e18 as enble_lltv
FROM morpho_blue_ethereum.MorphoBlue_evt_EnableLltv
ORDER BY
evt_block_number DESC
当用户的资产被清算时,根据 LTV 的情况,用户的抵押品价值实际上仍大于借出资产价值,此时我们是否应该为用户留下部分抵押品?
这里为了平衡清算者与借款者之间的利益,Morpho 引入了 LIF(Liquidation Incentive Factor) ,即清算激励因子。该因子的计算公式如下: $$ LIF = \min(M, \frac{1}{\beta * LLTV + (1 - \beta)}) $$ 其中 $\beta = 0.3$, $M = 1.15$。该函数对应有以下图像:
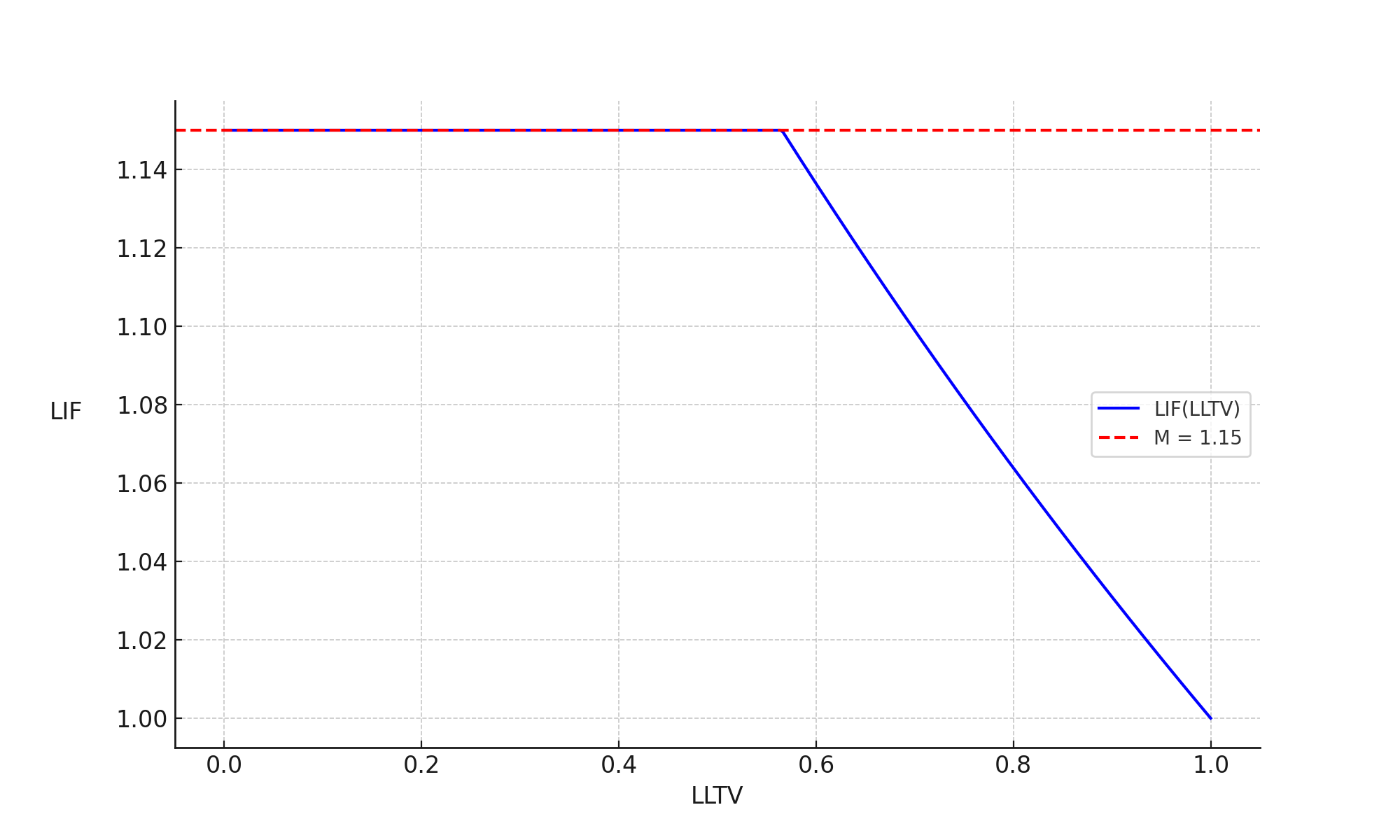
LIF 因子决定了清算结束后,用户剩余抵押品的数量。上述都是比较抽象的介绍,让我们直接看一个来自 morpho 文档 的示例。假设用户 A 在 LLTV = 80% 的市场内提供了 $100 的保证金 A。使用上述 LIF 公式计算可得,该市场的 LIF = 1.0638。当用户的借出资产价值大于 $80 时,用户处于清算状态。此时清算者帮助用户偿还借出资产,可以获得如下数量的保证金: $$ SeizableAssets = debtAmount∗LIF = 80 * 1.0638 = 85.104 $$ 我们可以发现此时用户还剩余 100 - 85.104 = 14.896 的担保品。可能有读者感觉官方案例没啥意思,让我们观察一个真实发生的 清算交易。在该交易的核心如下:
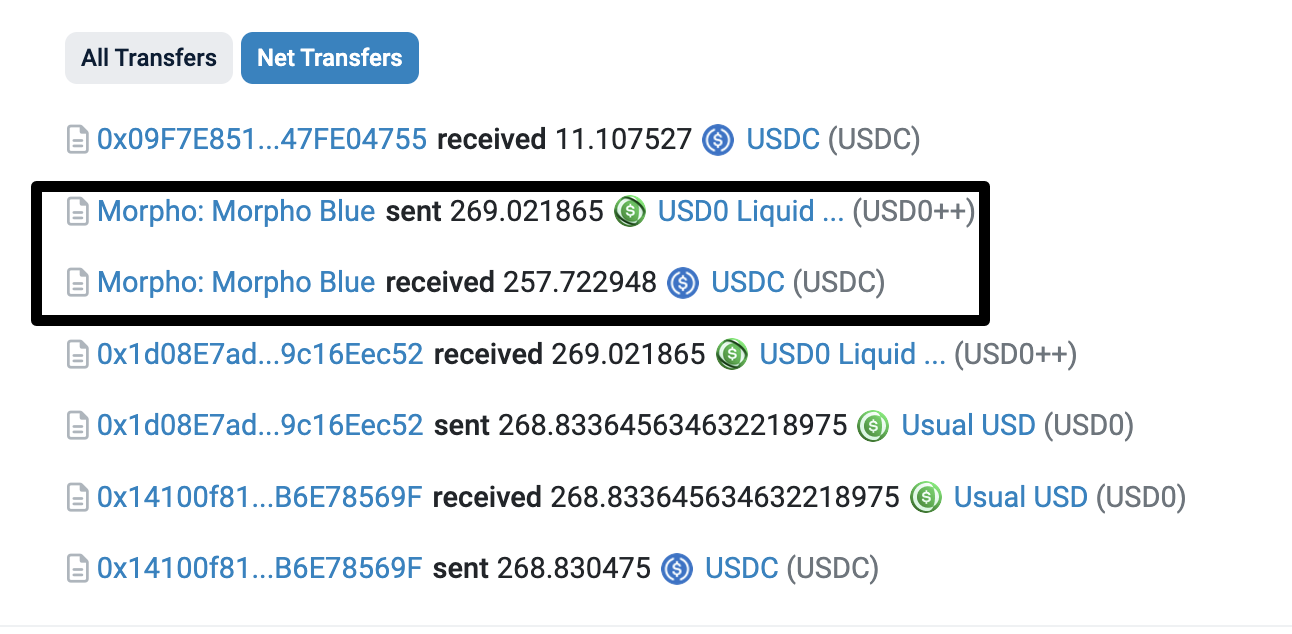
即清算者向 Morpho 发送了 257.772 USDC 但获得了 269.021 USD0,其他交易基本都是在 Curve 内进行资产兑换。在清算发送时,USD0 与 USDC 之间的汇率为 1。查询上述交易的 日志,我们可以看到交易发生的金库 ID。
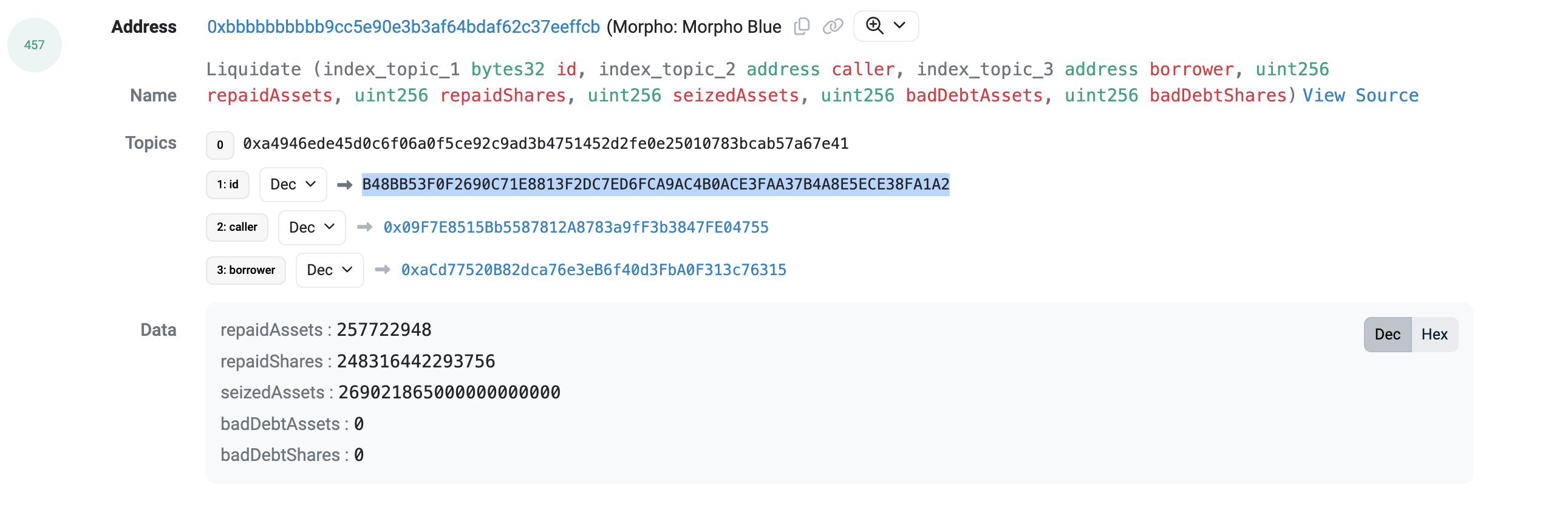
接下来,我们在 Morpho Etherscan 合约页面 调用 idToMarketParams 函数获取此金库的参数:
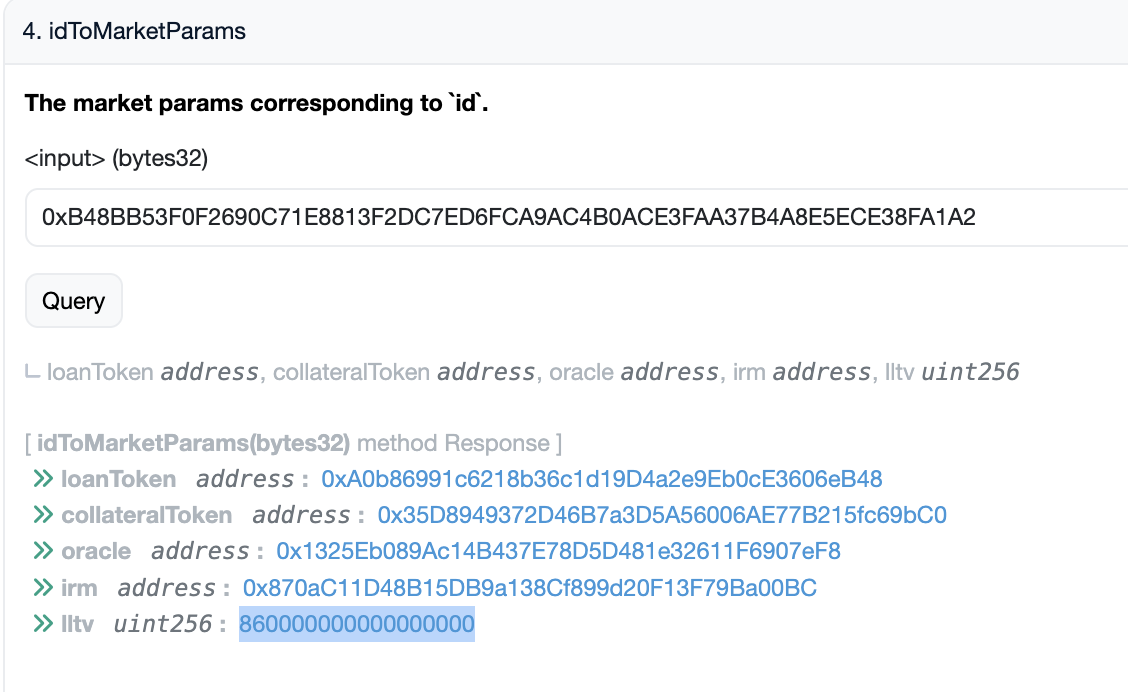
注意此处的 lltv 是具有 1e18 精度的,可以转化为 86%。由此,我们可以计算此金库的 LIF 为 1 / (0.3 * 0.86 + 0.7) = 1.0438。然后,当清算者输入 257.722948 USDC 时,理论上可以获得 269.02186 USD0 资产。这与合约显示是一致的。
以上就是 Morpho 的清算规则,相比于 AAVE V3 的 复杂规则,Morpho 的清算显然规则更加简单。而在利率模型(irm)方面,Morpho 要求用户使用的利率模型必须经过治理同意,目前事实上支持一种利率模型。如果读者希望知道 Morpho 启动的利率模型,可以随时使用以下 SQL 代码检索:
SELECT
*
FROM morpho_blue_ethereum.MorphoBlue_evt_EnableIrm
ORDER BY
evt_block_number DESC
目前返回结果只有两个 0x0000000000000000000000000000000000000000 和 0x870ac11d48b15db9a138cf899d20f13f79ba00bc。事实上,当使用零地址作为 IRM 时,等同于放弃借贷利率。
而 0x870ac11d48b15db9a138cf899d20f13f79ba00bc 则是 Morpho 主推的知名的 AdaptiveCurveIRM 模型。该模型来源于 PID 的思路。PID 是指使用当前系统的输出值与目标值之间的差距,利用多个分量计算当前系统的调整值。在借贷系统内,我们的目标值是一个合理的资金利用率($u_{target}$),而系统的输出值自然是当前的资金利用率($u(t)$)。可能有部分读者不熟悉资金利用率低概念,该概念定义如下:
$$
U = \frac{Total\ borrowed}{Total\ supplied}
$$
其中,参数含义如下:
Total borrowed该市场内资产总借出数量Total supplied该市场内资产总存入数量
假如市场内总计有 1000 USDC 存入,总计有 800 USDC 借出,那么该市场目前的资金利用率为 80%。
此处我们记目标值与当前系统资金利用率之间的差距为函数 $e(u)$。$e(u)$ 是一个对利用率的函数。最终的利率模型如下: $$ Ri = R{i - 1} e^{\text{speed}(t)}\ r_i = \text{curve}(e(u)) * R_i $$ 最新的利率 $r_i$ 取决于 $R_i$ 和一些调整因子。此处的 $R_i$ 实际上只用于最终计算 $r_i$,但由于 $Ri$ 的计算需要 $R{i - 1}$ ,所以在具体的实现中,我们每次都会将 $Ri$ 的计算结果存储到合约里以作为下一次计算时的 $R{i - 1}$ 因子。
上述公式内的 $\text{curve}(e(u))$ 和 $\text{speed(t)}$ 是一个特殊的函数。$\text{curve}(e(u))$ 是一个分段函数,当 $u < u_{target}$ 时,$\text{curve}(e(u)) < 1$,此时 $ri < r{i-1}$ ,通过利率下调激励用户借出更多资产。而当 $u > u_{target}$ 时,则 $ri > r{i-1}$ ,利率向上调整,激励用户偿还债务。而 $e^{\text{speed}(t)}$ 代表 $e(u)$ 与当前利率调整和上次利率调整之间的时间差的比值。当利用率长时间都处于低位时,该因子将小于 1 使得利率进一步降低;当利用率长时间处于高位时,$e^{\text{speed}(t)}$ 将大于 1 ,使得利率进一步拉升。
在此处 $e^{\text{speed}(t)}$ 实际上还有另一个作用,即在 $R_i$ 内部积累过去的 $e(u)$,如下: $$ \begin{align} Ri &= R{i-1}e^{\text{speed}(t{i-1})} \ &= R{i-2}e^{\text{speed}(t{i-1}) + \text{speed}(t{i-2})} \end{align} $$ 我们可以看到 $e^{\text{speed}(t)}$ 会在指数位置累计。由此实现一种特殊的效果,即单次的长时间利用率维持可以影响较长时间的未来利率。比如当前保持了长时间的低利用率,那么即使短期内利用率拉升也不会导致利率快速增加。这也是符合直觉的。
有了一个直观理解后,我们将详细介绍每一个函数的具体实现。首先是误差函数: $$ e(u) = \begin{cases} \frac{u(t) - u{target}}{1 - u{traget}} &\text{if } u(t) > u{traget} \ \frac{u(t) - u{target}}{u{traget}} &\text{if } u(t) \le u{traget} \end{cases} $$ 该函数代表当前利用率与目标利用率 $u_{target} = 90\%$ 之间的误差的规范化,将误差规整到 $[-1, 1]$ 的区间内。上述函数图像如下:
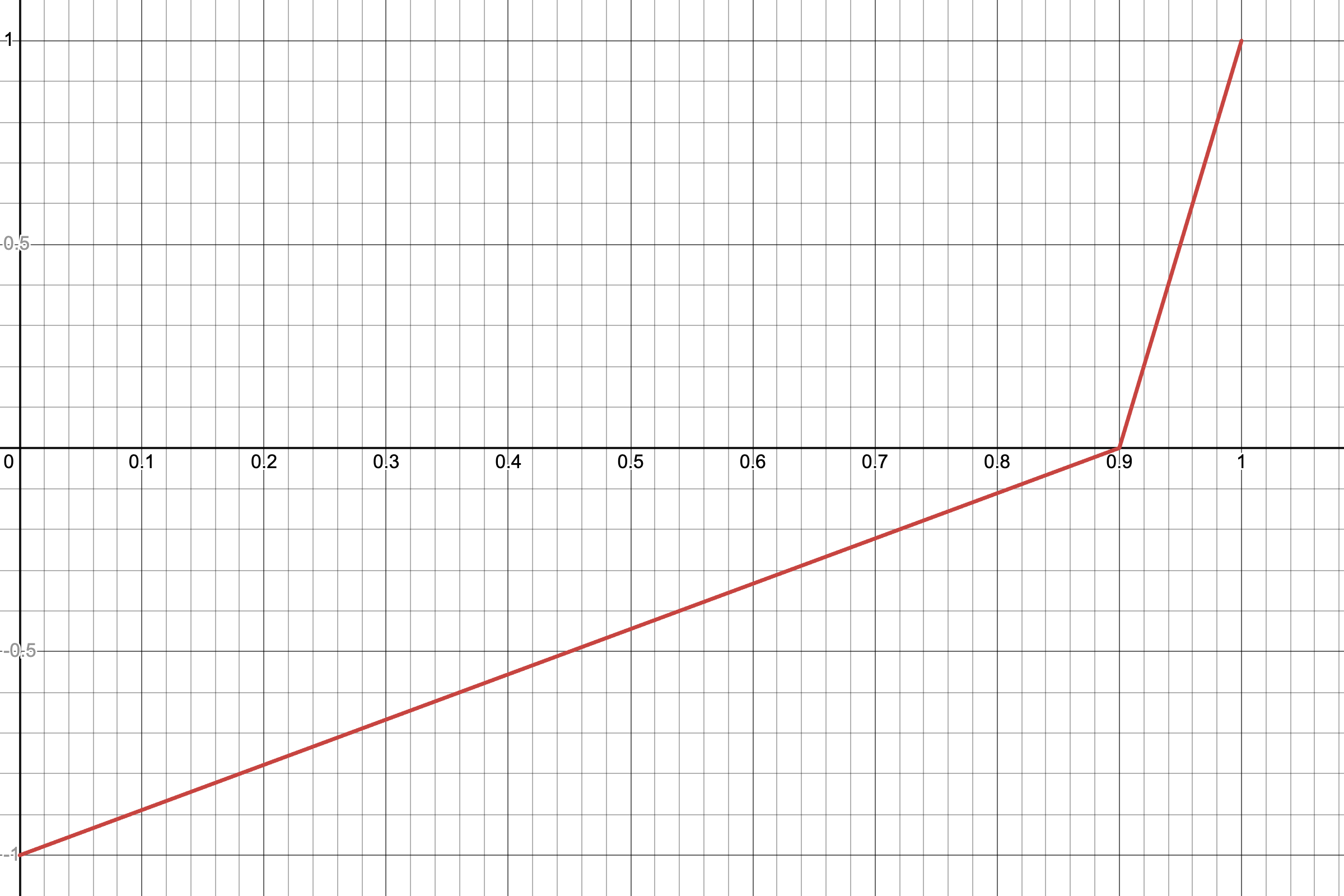
有了上述 $e(u)$ 函数,我们可以继续定义 $curve(u)$ 函数,该函数定义如下: $$ \text{curve}(u) =\begin{cases} (kd - 1) * e(u) + 1 &\text{if } u(t) > u{target} \ (1 - kd) * e(u) + 1 &\text{if } u(t) \le u{target} \end{cases} $$
该函数的图像如下:
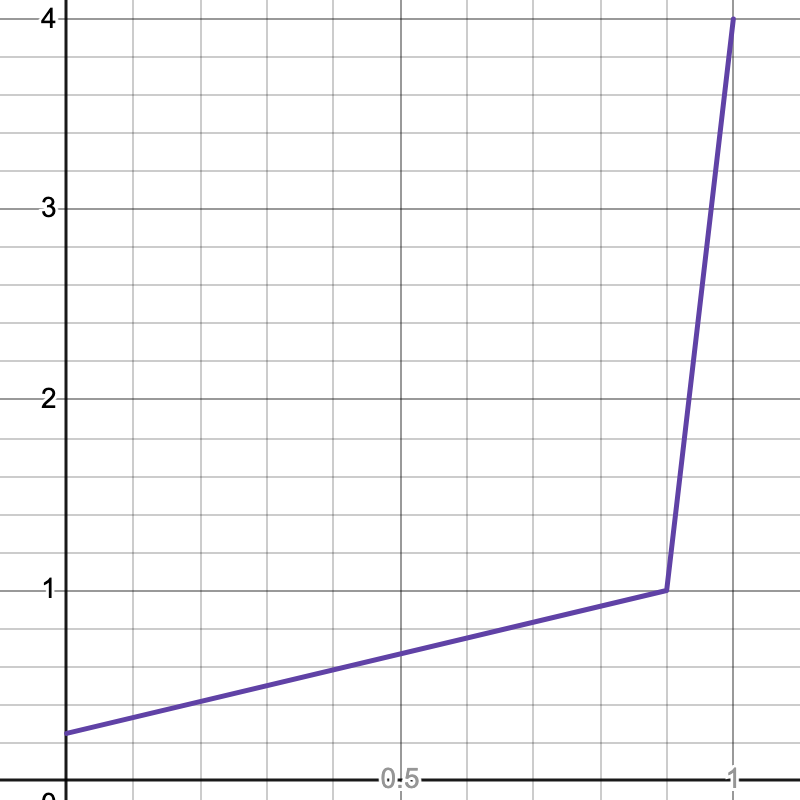
作为一个短期调节因子,$\text{curve}(u)$ 在 $u(t) > u_{traget}$ 时将快速拉高利率。而反之则降低利率。
最后,我们可以定义 $\text{speed(u)}$ 函数,为了与 Morpho 文档一致,我们此处定义的 $\text{speed(u)}$ 实际上是 $e^\text{speed(t)}$ 函数: $$ \text{speed}(u) = \exp\left(u(t)\cdot\frac{50 \times \Delta_t}{31556926}\right) $$ 此处的 $31556926$ 实际上是一年的秒数,我们可以理解为 $\text{speed}(t)$ 本质上是将 $u(t)$ 扩大 50 倍后拆分到一年内的每一秒,然后计算 $\Delta_t$ 时间段内的变化。正如上文所述,$\Delta_t$ 代表本次利率更新与上一次利率更新的时间差,该参数的单位为秒。由于该函数内的 $\Deltat$ 是动态的,我建议读者直接前往我为 Morpho 利率模型设计的 desmos 界面自己体验一下。函数 $f{speed}\left(x\right)$ 代表 $speed(u)$。
简单来说,当 $\Delta_t$ 越大时,该因子的范围也就越大,最终的效果是当 $\Delta_t$ 越大时,该因子对最终利率的影响越大。
按照上文定义,最终的利率模型为: $$ Ri = R{i - 1} \text{speed}(u) \ r_i = \text{curve}(e(u)) R_i $$
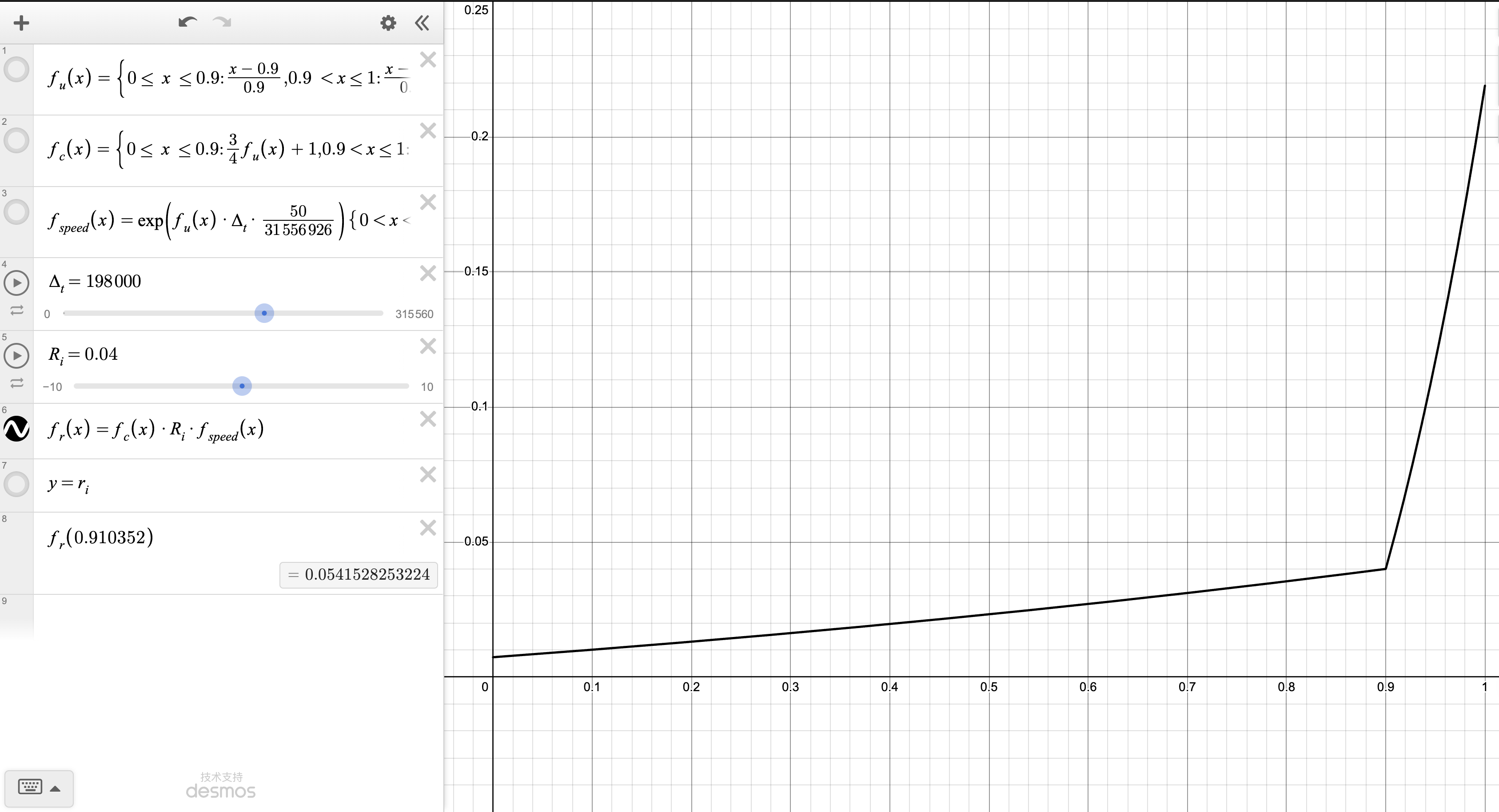
上述最终计算公式也可以在 desmos 页面内找到,该页面内的 $f_r(x)$ 即最终的利率计算公式,其中 $x$ 代表 $u$。当然为了避免利率过大或过低出现其他问题,Morpho 规定 $0.1\% < r_i < 200\%$。同时,设置最初的利率为 $r_0 = 4\%$。
上述公式存在一个问题,即上述公式实际上是假设 $\Delta_t \to 0$ 时的结果。当 $\Delta_t$ 是一个较大的数时,我们应该考虑使用平均利率计算,上述利率公式将演变为如下格式: $$ ri = \text{curve}(e(u)) * R{i - 1} * \frac{\int^{\Delta_t}_0\text{speed}(u)}{\Delta_t} $$ 关于如何求解上述公式,Morpho Bule 在源代码内使用了 Trapezoidal rule 来计算。我们会在后文介绍 IRM 源代码时进行详细分析。对于 $\Delta_t$ 不大的情况,实际上不使用积分也可以。
接下来,我们尝试计算一笔 真正的交易 的利率更新。该交易的交易对象是 wstETH / USDC 金库。查询该交易的 BorrowRateUpdate 日志可以看到如下信息:
avgBorrowRate: 2288292706
rateAtTarget: 2288771456
此处的 avgBorrowRate 就是当前的利率,也是积分后获得的利率,该利率用于用户的利息计算。而 rateAtTarget 就是没有经过积分直接计算的利率,该利率也是用于下一次利息计算的 $r_{i-1}$。无论是 avgBorrowRate 还是 rateAtTarget 都是秒利率,即一秒内的利率。我们可以通过 $2288771456 / 1e18 31556926 100\% = 7.222659\%$ 获得年华利率。
该交易完成后,经过 111 个区块(1322 秒)后,这个金库又被 另一笔交易 更新,更新后的利率信息为:
avgBorrowRate: 2999884861 (9.4667144567%)
我们尝试使用第一笔交易后的参数计算第二笔交易的利率。此时,我们还缺少第一笔交易后的资金利用率数据,在此处我们不加解释的给出如下数据:
totalSupplyAssets: 41541304907552
totalBorrowAssets: 37817200712817
上述结果来自
cast call 0xBBBBBbbBBb9cC5e90e3b3Af64bdAF62C37EEFFCb "market(bytes32)((uint128,uint128,uint128,uint128,uint128,uint128))" 0xb323495f7e4148be5643a4ea4a8221eef163e4bccfdedc2a6f4696baacbc86cc -b 21307370命令。market函数会返回一个包含总存入资产和总借出资产的结构体。我们会在后文进一步介绍
计算可得 $u = 37817200712817 / 41541304907552 = 91.0352$。将 $R_{i - 1} = 7.222659\%$ , $\Delta_t = 1322$ 和 $u$ 代入公式,最终计算结果如下:
我们可以看到使用我们的计算工具计算获得的结果与直接在链上获取的结果是基本一致的。由此,我们就全面介绍了 Morpho 的基于 LIF 的清算规则和复杂的利率曲线。
预言机
在后文介绍 Morpho 的核心代码时,我们将按照创建市场并设置参数、存入资产、借出资产和清算的流程进行介绍。但创建市场时是需要预言机的。为了保证用户的阅读体验,我们将首先介绍预言机模块。注意,本文内的所有操作都将在 base 主网上进行。读者需要在 Base 主网内持有少量 ETH。预言机的部署将花费 0.11 美元 ETH。
由于 Morpho 目前主要支持 Chainlink 的预言机,所以在介绍具体的预言机之前,我们首先需要了解 Chainlink 的一些技术细节。Chainlink 在链上部署了一系列的预言机合约,这些合约会为用户提供最新的资产价格数据。读者可以在 此处 找到 Chainlink 部署好的预言机。此处以 Base 上的 BTC / USD 预言机为例,我们可以通过读取该合约的 latestRoundData 函数获得最新的 BTC 价格数据。阅读该预言机对应的合约,我们会发现 latestRoundData 函数调用了其他合约。
function latestRoundData()
public
view
virtual
override
returns (
uint80 roundId,
int256 answer,
uint256 startedAt,
uint256 updatedAt,
uint80 answeredInRound
)
{
Phase memory current = currentPhase; // cache storage reads
(
uint80 roundId,
int256 answer,
uint256 startedAt,
uint256 updatedAt,
uint80 ansIn
) = current.aggregator.latestRoundData();
return addPhaseIds(roundId, answer, startedAt, updatedAt, ansIn, current.id);
}
这是因为我们直接交互 Chainlink 预言机基本都是使用了类似代理部署的模式,真实的数据存储在另一个合约内,即上文的 current.aggregator 合约内部(在后文内,我们称其为聚合器合约)。而价格数据更新也都发生在 current.aggregator 合约内部。使用这套类似代理部署的原因是 Chainlink 也存在智能合约更新的可能性,但大部分情况下,用户都是将预言机地址硬编码在自己的合约内部。为了避免 Chainlink 合约升级造成毁灭性后果,Chainlink 选择了类似代理部署的模式。当需要更新自己的合约时,只需要将预言机地址指向新的合约即可。
对于返回值,我们只需要 answer 即可,该返回值代表价格数据。而 roundId 和 answeredInRound 代表当前正在进行的轮次和返回数据所在的轮次。由于 Chainlink 目前使用了链下数据聚合方案, roundId 和 answeredInRound 都是一致的。
我们可以通过以下命令查询到 Base 主网上的 BTC / USD 合约背后的聚合器合约:
cast call 0x64c911996D3c6aC71f9b455B1E8E7266BcbD848F "latestRoundData()(uint80 roundId, int256 answer, uint256 startedAt, uint256 updatedAt, uint80 answeredInRound)" --trace
结果如下:
Traces:
[15735] 0x64c911996D3c6aC71f9b455B1E8E7266BcbD848F::latestRoundData()
├─ [7502] 0x852aE0B1Af1aAeDB0fC4428B4B24420780976ca8::latestRoundData() [staticcall]
│ └─ ← [Return] 0x000000000000000000000000000000000000000000000000000000000000f1f8000000000000000000000000000000000000000000000000000008a78510524000000000000000000000000000000000000000000000000000000000674f391700000000000000000000000000000000000000000000000000000000674f3917000000000000000000000000000000000000000000000000000000000000f1f8
└─ ← [Return] 0x000000000000000000000000000000000000000000000001000000000000f1f8000000000000000000000000000000000000000000000000000008a78510524000000000000000000000000000000000000000000000000000000000674f391700000000000000000000000000000000000000000000000000000000674f3917000000000000000000000000000000000000000000000001000000000000f1f8
我们可以看到聚合器合约的地址为 0x852aE0B1Af1aAeDB0fC4428B4B24420780976ca8。我们可以在 区块链浏览器 内看到该合约被不断交互以更新价格数据:
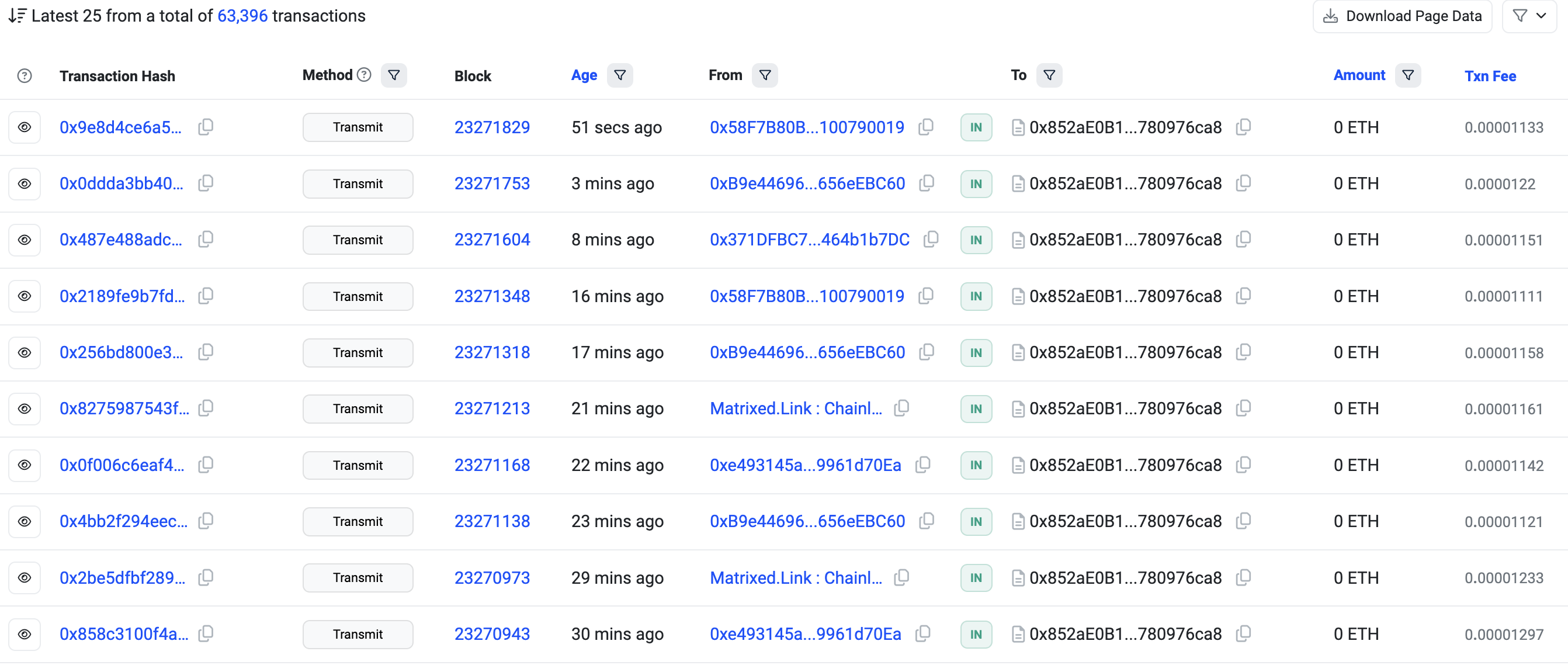
上述调用的 transmit 函数实际上就是 Chainlink Oracle 网络调用来更新价格数据的。在最新版本的实现内,Chainlink Oracle 网络将在自己的网络内实现对价格信息的共识,然后将最终的价格信息签名后上链所以我们不会在链上看到一些价格信息计算的逻辑,这部分逻辑完全在 Chainlink 的网络内完成。但我们可以在 transmit 函数内部观察到签名的校验。该价格更新环节被称为 Offchain Reporting (OCR),更多信息可以参考 白皮书 或者阅读 How Chainlink Price Feeds Work 一文。
预言机是一个有趣的方向。如果读者熟悉 MEV,就会发现预言机也是有 MEV 的机会的,这些 MEV 机会往往会被进一步细分为 OEV。更多关于预言机的资料可以参考 Exploring the Design Space and Challenges for Oracle Implementations in DeFi Protocols。
在了解了 Chainlink 预言机的工作原理后,我们就可以查看 morpho 此部分的源代码。我们首先 clone 相关源代码,如下:
git clone https://github.com/morpho-org/morpho-blue-oracles.git
Morpho 为了方便用户构建预言机,直接部署一个预言机的工厂合约。该合约在 Base 主网上的地址为 0x2DC205F24BCb6B311E5cdf0745B0741648Aebd3d,其源代码位于 src/morpho-chainlink/MorphoChainlinkOracleV2Factory.sol 内部。Morpho 的预言机使用一个非常有趣的链式计算的方案。在构造预言机时,用户最多可以指定 4 个预言机地址,分别称为 baseFeed1 / baseFeed2 / quoteFeed1 / quoteFeed2。这四个预言机以此提供以下价格数据:
baseFeed1提供B1资产与B2资产的汇率 $pB_1$,即一单位 B1 可以兑换 $pB_1$ 单位 B2baseFeed2提供B2资产与C资产的汇率 $pB_2$,即一单位 B1 可以兑换 $pB_2$ 单位 CquoteFeed1提供Q1资产与Q2资产的汇率 $pQ_1$,即一单位 Q1 可以兑换 $pQ_1$ 单位 Q2quoteFeed2提供Q2资产与C资产的汇率 $pQ_2$,即一单位 Q2 可以兑换 $pQ_2$ 单位 C
在最终的价格计算过程中,Morpho 将使用以下方法计算最终的价格:
$$
price = \frac{pB_1 \times pB_2}{pQ_1 \times pQ_2}
$$
注意,我们可以通过将预言机的地址置为零地址实现将某一个汇率转化为 1。比如将 quoteFeed2 设置为零地址,那么 $pQ_2$ 就会被置为 0。
我们可以举几个例子来说明如何使用上述预言机:
第一个例子,直接将某一个 Chainlink 已经给出的预言机转化为 Morpho 中的预言机。比如 此交易 创建的 HETH / ETH 的预言机,该交易给出了以下参数:
"baseFeed1": "0x027A9CFcBB53cbB1721B495c2dcaF54d4cF33106",
"baseFeed2": "0x0000000000000000000000000000000000000000",
"quoteFeed1": "0x0000000000000000000000000000000000000000",
"quoteFeed2": "0x0000000000000000000000000000000000000000",
其中 baseFeed1 就是 HETH / ETH 的价格预言机。
第二个例子,将某一个预言机反转。比如将 USDC / USD 反转为 USD / USDC。比如 此交易 创建了一个特殊的预言机,该交易参数如下:
"baseVault": "0x07D1718fF05a8C53C8F05aDAEd57C0d672945f9a"
"baseFeed1": "0x0000000000000000000000000000000000000000",
"baseFeed2": "0x0000000000000000000000000000000000000000",
"quoteFeed1": "0x8fFfFfd4AfB6115b954Bd326cbe7B4BA576818f6",
"quoteFeed2": "0x0000000000000000000000000000000000000000",
上述预言机被用于 arUSD / USDC 金库。此处的 baseVault 就是 arUSD 的地址。arUSD 是一种基于 ERC4626 的代币,具体可以参考 此文档。简单来说,arUSD 是用户存入 rUSD 获得的,但 arUSD 是具有利息的,当用户持有 arUSD 越久,兑换回的 rUSD 越多。对于这种基于 ERC4626 的生息代币往往没有预言机,但是这类代币都提供了 convertToAssets 计算代币转化为底层资产的比率。在 Morpho 的预言机合约内,自动实现了此变换,当用户指定 baseVault 时,Morpho 预言机在计算价格时,会自动转化 ERC4626 代币为底层代币。比如在上述预言机内,当用户输入 baseVault 参数时,预言机会自动计算 arUSD / rUSD 的比率,然后在于其他预言机等产生的价格相乘或相除。
由于上述预言机使用了将 quoteFeed1 置为 0x8fFfFfd4AfB6115b954Bd326cbe7B4BA576818f6 ,该地址是 USDC / USD 的预言机地址。那么最终 Morpho 预言机产生的价格等于 (arUSD / rUSD) / (USDC / USD)。这里预言机的创建者实际上假设了 rUSD 不会脱锚,即 1 rUSD = 1 USD 恒成立。由此就可以进行以下推导:
$$ \begin{align} price &= \frac{arUSD}{rUSD} / \frac{USDC}{USD} \ &= \frac{arUSD}{USD} \times \frac{USD}{USDC} (1 rUSD = 1 USD) \ &= \frac{arUSD}{USDC} \end{align} $$
实际上更好的方案是指定
baseFeed1为rUSD / USD的预言机,由此计算的价格更加准确。但是我们也可以理解上述行为,因为没有任何 rUSD 的利益相关方认为 rUSD 会脱锚
第三个例子,通过连续指定 baseFeed1 和 baseFeed2 来进行链式预言机价格计算。当然,同时指定 quoteFeed1 和 quoteFeed2 也可以实现链式的价格计算。这里以 此交易 为例。该交易构建了 SolvBTC / USD 的预言机。该预言机使用了 SolvBTC / BTC 和 BTC / USD 两个预言机拼接产生,使用了如下参数:
"baseFeed1": "0x936b31c428c29713343e05d631e69304f5cf5f49",
"baseFeed2": "0xf4030086522a5beea4988f8ca5b36dbc97bee88c",
"quoteFeed1": "0x0000000000000000000000000000000000000000",
"quoteFeed2": "0x0000000000000000000000000000000000000000",
具体推导较为简单,读者可以自行完成。
最后,我们可以混合上述多个 Feed 实现更加复杂的预言机构造,比如此交易构建的 wstETH / tBTC 预言机。该交易使用了一下参数:
"baseFeed1": "0x4F67e4d9BD67eFa28236013288737D39AeF48e79", // wstETH / ETH
"baseFeed2": "0x5f4eC3Df9cbd43714FE2740f5E3616155c5b8419", // ETH / USD
"quoteFeed1": "0x8350b7De6a6a2C1368E7D4Bd968190e13E354297", // tBTC / USD
"quoteFeed2": "0x0000000000000000000000000000000000000000",
我们可以使用以下方法推导该预言机的类型: $$ \begin{align} price &= \frac{wstETH / ETH \times ETH / USD}{tBTC / USD} \ &= \frac{wstETH / USD}{tBTC / USD} \ &= wstETH / tBTC \end{align} $$ 使用上述方法读者可以任意构建任意的预言机。
本文内给出的所有示例都是使用 Dune 检索获得的。读者可以使用在 Dune 内使用以下代码检索主网预言机:
SELECT call_tx_hash, baseFeed1, baseFeed2, quoteFeed1, quoteFeed2, output_oracle FROM morpho_blue_ethereum.MorphoChainlinkOracleV2Factory_call_createMorphoChainlinkOracleV2 WHERE baseFeed1 != 0x0000000000000000000000000000000000000000 AND baseFeed2 != 0x0000000000000000000000000000000000000000 AND quoteFeed2 = 0x0000000000000000000000000000000000000000 AND quoteFeed1 != 0x0000000000000000000000000000000000000000 AND call_success = true ORDER BY call_block_number DESC LIMIT 10;
在了解了 Morpho 预言机的基本原理后,我们就可以直接来看相关源代码。Morpho 预言机的源代码位于 src/morpho-chainlink/MorphoChainlinkOracleV2.sol 内部。我们首先观察该预言机的构造器:
constructor(
IERC4626 baseVault,
uint256 baseVaultConversionSample,
AggregatorV3Interface baseFeed1,
AggregatorV3Interface baseFeed2,
uint256 baseTokenDecimals,
IERC4626 quoteVault,
uint256 quoteVaultConversionSample,
AggregatorV3Interface quoteFeed1,
AggregatorV3Interface quoteFeed2,
uint256 quoteTokenDecimals
) {}
其构造器需要较多变量,这些变量的含义大部分读者应该已经知道。其中 quoteVault 在上文并没有出现过,该参数与 baseVault 类似,代表某种 ERC4626 代币的价格,只是位于分母位置而已。当创建使用某些资产贷出 ERC4626 资产时会使用到此参数。
而 baseVaultConversionSample 和 quoteVaultConversionSample 是用于处理不同精度的 share 的参数。在使用 ERC4626 资产时,我们需要调用 ERC4626 金库的 convertToAssets 函数,此时需要传入 share 的数量,而 baseVaultConversionSample 和 quoteVaultConversionSample 分别代表在 baseVault 和 quoteVault 进行份额转化时需要传入的 share 的数量。
其他参数如 baseTokenDecimals 和 quoteTokenDecimals 代表最终产生的预言机的资产精度。如 arUSD / USDC 预言机,该预言机使用 arUSD 具有 18 位精度,而 USDC 则只有 6 位精度,所以在构建此预言机时,传入 baseTokenDecimals 参数为 18 而 quoteTokenDecimals 参数为 6。
接下来,我们需要做一个非常复杂的推导获得缩放因子。我们首先将上文出现的公式纳入精度处理(以下公式内出现的 $dB_1$ 和 $dB_2$ 等代表代币的精度): $$ \begin{align} scale &= \frac{ 10^{36} \times pB_1 \times 10^{dB_2 - dB_1}\times pB_2 \times 10^{dC - dB_2} }{ pQ_1 \times 10^{dQ_2 - dQ_1} \times pQ_2 \times 10^{dC - dQ_2} } \ &= \frac{10^{36} \times pB_1 \times 10^{- dB_1} \times pB_2 }{pQ_1 \times 10^{- dQ_1}\times pQ_2} \end{align} $$
上述公式内的 $10^{36}$ 是为了放大分子以避免精度损失,而 $10^{dB_2 - dB_1}$ 等都是在调整精度。这些因子使得 $pB_1$ 精度归一。根据 $1\times 10^{dB_1} = pB_1 \times 10^{dB_2}$ 的定义。$pB_1$ 天然具有 $10^{dB_1 - dB_2}$ 的精度,而上述共识内的 $10^{dB_2 - dB_1}$ 就是为了去掉此精度。其他如 $10^{dQ_2 - dQ_1}$ 的也是同理获得的。需要注意,上述公式内的 $pB_1$ 实际上还有一个精度,这是因为预言机在返回的实际上是定点小数,我们可以通过调用预言机的 decimals 函数获取。我们需要消除掉这些定点小数的影响。
$$
\begin{align}
scale &= \frac{10^{36} \times pB_1 \times 10^{- dB_1} \times pB_2 }{pQ_1 \times 10^{- dQ_1}\times pQ_2} \
&= \frac{10^{36} \times \frac{pB_1}{fpB_1} \times 10^{- dB_1} \times \frac{pB_2}{fpB_2} }{\frac{pQ_1}{fpQ_1} \times 10^{- dQ_1}\times \frac{pQ_2}{fpQ_2}}
\end{align}
$$
上述公式内的 $fpB_1$ 等即代表 $pB_1$ 预言机的精度。在只考虑 scale 的指数的情况下,我们可以获得如下结果:
$$
\text{Scale Factor} = 36 + fpQ_1 + fpQ_2 + dQ_1 - fpB_1 - fpB_2 - dB_1
$$
由此,我们就获得了 MorphoChainlinkOracleV2 构造器的如下代码:
SCALE_FACTOR = 10
** (
36 + quoteTokenDecimals + quoteFeed1.getDecimals() + quoteFeed2.getDecimals() - baseTokenDecimals
- baseFeed1.getDecimals() - baseFeed2.getDecimals()
) * quoteVaultConversionSample / baseVaultConversionSample;
而最后的利率修正是为了避免 ERC4626 金库的影响。计算总体放缩因子的核心在于首先确认最终结果的公式,如在此处就是首先需要确定 price 的计算公式。然后将计算公式内所有含精度的因子精度去掉由此获得最终的放缩因子。
当我们获得放缩因子后,就可以直接使用以下函数计算获得 price:
function price() external view returns (uint256) {
return SCALE_FACTOR.mulDiv(
BASE_VAULT.getAssets(BASE_VAULT_CONVERSION_SAMPLE) * BASE_FEED_1.getPrice() * BASE_FEED_2.getPrice(),
QUOTE_VAULT.getAssets(QUOTE_VAULT_CONVERSION_SAMPLE) * QUOTE_FEED_1.getPrice() * QUOTE_FEED_2.getPrice()
);
}
此处的 mulDiv 来自 openzeppelin-contracts 的数学计算库。在此处不再进一步介绍。
核心代码
在介绍完预言机后,我们正式进入 Morpho Bule 的核心代码部分,我们将按照以下几个部分逐步介绍核心代码的部分:
- 创建市场(
createMarket)。正如其名,主要介绍创建市场所需要的参数 - 资产存入和提款。主要介绍存入资产(
supply) 和 提取资产(withdraw)。注意,此处存入的资产可以获得利息,而提取资产时也可以获得利息和本金 - 存入和提取担保品。与 AAVE 等借贷协议,用户不能直接使用自己存入的资产直接进行借款,而是需要单独为借款存入担保品(
supplyCollateral),且担保品不具有利息收入。而提取担保品需要使用withdrawCollateral方法。 - 借款和偿还借款。主要介绍借出资产(
borrow) 和 偿还借款(repay)。注意,此处借出的资产需要支付利息,而偿还时也需要支付利息和借款 - 清算借贷仓位。主要介绍
liquidate清算函数。
与其他借贷协议一致,Morpho Bule 使用了基于 share 的利息计算方案,无论是存款利息和借款利息都使用了此方案。关于 Share 的计算,我们会在下一节介绍,本节不会详细介绍 Share 计算过程。
创建市场
创建市场是一个相对简单的动作。 用户需要提供以下结构体:
struct MarketParams {
address loanToken;
address collateralToken;
address oracle;
address irm;
uint256 lltv;
}
其中, loanToken 指可以借出的资产,而 collateralToken 代表作为担保品的资产。 oracle 是我们在上一节介绍的预言机的地址,注意在最终计算仓位是否健康时,我们会使用用户仓位的担保品数量乘以预言机的返回值,故而预言机应该是 collateralToken / loanToken 的形式。
function createMarket(MarketParams memory marketParams) external {
Id id = marketParams.id();
require(isIrmEnabled[marketParams.irm], ErrorsLib.IRM_NOT_ENABLED);
require(isLltvEnabled[marketParams.lltv], ErrorsLib.LLTV_NOT_ENABLED);
require(market[id].lastUpdate == 0, ErrorsLib.MARKET_ALREADY_CREATED);
// Safe "unchecked" cast.
market[id].lastUpdate = uint128(block.timestamp);
idToMarketParams[id] = marketParams;
emit EventsLib.CreateMarket(id, marketParams);
// Call to initialize the IRM in case it is stateful.
if (marketParams.irm != address(0)) IIrm(marketParams.irm).borrowRate(marketParams, market[id]);
}
用户需要最终使用 createMarket 函数创建市场。在 createMarket 函数内,我们可以第一步就进行 id 计算,计算方法如下:
uint256 internal constant MARKET_PARAMS_BYTES_LENGTH = 5 * 32;
function id(MarketParams memory marketParams) internal pure returns (Id marketParamsId) {
assembly ("memory-safe") {
marketParamsId := keccak256(marketParams, MARKET_PARAMS_BYTES_LENGTH)
}
}
实际上就是将输出的参数进行 keccak256 哈希处理。由于 marketParams 长度是固定的 MARKET_PARAMS_BYTES_LENGTH,所以此处直接使用了固定的长度。在内存内, struct 不会进行压缩处理,结构体内的每一项都将占据 32 bytes 的空间,所以此处的 MARKET_PARAMS_BYTES_LENGTH = 5 * 32 。
在完成 id 计算后,我们可以看到代码进行了一系列检查。其中 isIrmEnabled 检测用户是否使用了官方认可的 IRM。正如上文所述,目前 Morpho 仅允许用户使用零地址和 AdaptiveCurveIRM 模型。我们在上文内已给出了相关地址。然后检查 isLltvEnabled 是否被允许,在上文内,我们介绍过 Morpho Bule 仅允许用户使用 [0%; 38.5%; 62.5%; 77.0%; 86.0%; 91.5%; 94.5%; 96.5%; 98%] 几个档次的 LLTV。最后检查 market[id].lastUpdate 来判断当前市场是否已被创建。 market 是一个如下映射的储存类似:
type Id is bytes32;
mapping(Id => Market) public market;
struct Market {
uint128 totalSupplyAssets;
uint128 totalSupplyShares;
uint128 totalBorrowAssets;
uint128 totalBorrowShares;
uint128 lastUpdate;
uint128 fee;
}
我们可以看到 Market 结构体内记录了金库的核心参数。我们会发现用于创建金库时传入的 MarketParams 并不包含 fee 字段,而 Market 结构体内则包含 fee 字段。因为 fee 字段实际上是 Morpho Bule 的管理员后期调用函数增加的:
/// @inheritdoc IMorphoBase
function setFee(MarketParams memory marketParams, uint256 newFee) external onlyOwner {
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(newFee != market[id].fee, ErrorsLib.ALREADY_SET);
require(newFee <= MAX_FEE, ErrorsLib.MAX_FEE_EXCEEDED);
// Accrue interest using the previous fee set before changing it.
_accrueInterest(marketParams, id);
// Safe "unchecked" cast.
market[id].fee = uint128(newFee);
emit EventsLib.SetFee(id, newFee);
}
/// @inheritdoc IMorphoBase
function setFeeRecipient(address newFeeRecipient) external onlyOwner {
require(newFeeRecipient != feeRecipient, ErrorsLib.ALREADY_SET);
feeRecipient = newFeeRecipient;
emit EventsLib.SetFeeRecipient(newFeeRecipient);
}
在完成所有的检查任务后, createMarket 函数将用户创建市场的信息写入存储,并调用 IRM 的 borrowRate 以实现 IRM 的初始化,由此就完成了最初的市场创建。
资产存入和提款
当用户存入资产后,该资产将会被出借,存入资产的用户获得收益。而提款则是提取自己的存入资产以及可能的利息。所以资产的存入和提取都是存在利息计算操作的。我们首先介绍利息计算操作对应的函数 _accrueInterest。该内部函数对应的代码如下:
function _accrueInterest(MarketParams memory marketParams, Id id) internal {
uint256 elapsed = block.timestamp - market[id].lastUpdate;
if (elapsed == 0) return;
if (marketParams.irm != address(0)) {
uint256 borrowRate = IIrm(marketParams.irm).borrowRate(marketParams, market[id]);
uint256 interest = market[id].totalBorrowAssets.wMulDown(borrowRate.wTaylorCompounded(elapsed));
market[id].totalBorrowAssets += interest.toUint128();
market[id].totalSupplyAssets += interest.toUint128();
uint256 feeShares;
if (market[id].fee != 0) {
uint256 feeAmount = interest.wMulDown(market[id].fee);
feeShares =
feeAmount.toSharesDown(market[id].totalSupplyAssets - feeAmount, market[id].totalSupplyShares);
position[id][feeRecipient].supplyShares += feeShares;
market[id].totalSupplyShares += feeShares.toUint128();
}
emit EventsLib.AccrueInterest(id, borrowRate, interest, feeShares);
}
// Safe "unchecked" cast.
market[id].lastUpdate = uint128(block.timestamp);
}
当需要累积利息时,我们首先调用 IRM 的 borrowRate 函数获得当前的借款利息,然后使用利息计算公式计算本次利息计算与上一次的利息计算的时间间隔内的利息收益。此处在计算利息时使用了 wTaylorCompounded 函数,该函数实际上用于计算 $e^x - 1$ 。如果读者熟悉利率市场,就会知道 $e^x - 1$ 是用于计算连续复利的手段。当使用利率完成利息计算后,我们将利息累加到 totalBorrowAssets 和 totalSupplyAssets 的资产范围内。
此时,假如当前金库存在手续费,那么我们需要将利息中的一部分提取给手续费。那么问题来了,手续费该如何提取?一种简单的方案是我直接把手续费记录到一个变量里,直接累加到该存储变量,这种常见方案最大的问题在于将手续费的逻辑完全独立。另一种方案是我们将手续费接受者( feeRecipient) 视为存款人,而手续费只是为 feeRecipient 增加的存款,以此我们可以统一手续费逻辑和存款逻辑。
在 Morpho Bule 内,利息的分配主要使用了 ERC4626 内的 share 逻辑。简单来说,我们可以通过以下公式计算 share:
$$
\begin{align}
share &= \frac{deposit}{total\ asset} \times total\ share \
&= \frac{deposit \times total\ share}{total\ asset}
\end{align}
$$
存入资产占 当前总资产(注意,不包含存入资产)的比值与当前的总 share 相乘就可以获得存入资产可转换的 share。当然,为了避免精度损失,我们往往在 solidity 实现时,先进行乘法计算,然后进行除法计算。使用 share 的好处在于,对于利息或者质押收益,我们可以直接将其累加到 $total\ asset$ 内部,此时收益等同于分配给了所有的 share 持有者。同时,对于利息分配后进入的用户,由于 share 机制的存在,其无法获得之前的利息,只能获得在此后累加的利息。简单来说,share 机制大幅度降低了复杂的利息计算逻辑。
如果读者希望进一步了解 share 的一些机制,建议阅读 ERC4626 Interface Explained
在 Marpho Bule 内, src/libraries/SharesMathLib.sol 库提供了 share 和 asset 之间的转化函数:
/// @dev Calculates the value of `assets` quoted in shares, rounding down.
function toSharesDown(uint256 assets, uint256 totalAssets, uint256 totalShares) internal pure returns (uint256) {
return assets.mulDivDown(totalShares + VIRTUAL_SHARES, totalAssets + VIRTUAL_ASSETS);
}
/// @dev Calculates the value of `shares` quoted in assets, rounding down.
function toAssetsDown(uint256 shares, uint256 totalAssets, uint256 totalShares) internal pure returns (uint256) {
return shares.mulDivDown(totalAssets + VIRTUAL_ASSETS, totalShares + VIRTUAL_SHARES);
}
此处的 VIRTUAL_SHARES 和 VIRTUAL_ASSETS 都是用来对抗一种特殊的针对 ERC4626 Share 机制的 Inflation attack,具体可以参考 Openzeppelin 文档。当然,我们看到的 toSharesDown 和 toAssetsDown 都是在计算过程中向下取整的,实际上 ShareMathLib 库内部还包含两个用于向上取整的 toSharesUp 和 toSharesUp 函数。
继续回到 _accrueInterest 内部的 feeShares 计算,我们发现在计算 feeShares 时使用了 market[id].totalSupplyAssets - feeAmount 作为 assets 而不是 market[id].totalSupplyAssets。这是因为我们计算 share 时只是使用当前的 total asset,即用户存款前的 total asset。在计算 feeShares 前,我们使用 market[id].totalSupplyAssets += interest.toUint128(); 将包含 fee 在内的利息累加进了 market[id].totalSupplyAssets,所以此处需要减去feeAmount变量。另外,我们还发现计算feeShares时使用了toSharesDown函数,这是因为在 Morpho Bule 内,计算存款时一律使用toSharesDown 函数,以此将误差损失过渡给用户。
最后,我们释放事件,并更新时间以保证下一次利率计算的正确。当我们介绍完成利率计算部分后,我们将介绍负责资产存入的 supply 函数,该函数的代码如下:
function supply(
MarketParams memory marketParams,
uint256 assets,
uint256 shares,
address onBehalf,
bytes calldata data
) external returns (uint256, uint256) {
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(UtilsLib.exactlyOneZero(assets, shares), ErrorsLib.INCONSISTENT_INPUT);
require(onBehalf != address(0), ErrorsLib.ZERO_ADDRESS);
_accrueInterest(marketParams, id);
if (assets > 0) shares = assets.toSharesDown(market[id].totalSupplyAssets, market[id].totalSupplyShares);
else assets = shares.toAssetsUp(market[id].totalSupplyAssets, market[id].totalSupplyShares);
position[id][onBehalf].supplyShares += shares;
market[id].totalSupplyShares += shares.toUint128();
market[id].totalSupplyAssets += assets.toUint128();
emit EventsLib.Supply(id, msg.sender, onBehalf, assets, shares);
if (data.length > 0) IMorphoSupplyCallback(msg.sender).onMorphoSupply(assets, data);
IERC20(marketParams.loanToken).safeTransferFrom(msg.sender, address(this), assets);
return (assets, shares);
}
在 Morpho Bule 内,为了降低读取市场设置的 gas 费用,Morpho Bule 要求用户调用函数时必须携带 MarketParams 结构体,而 Morpho Bule 会计算结构体哈希后获得的 id 以此判断结构体对应的市场是否被部署。在后文内,我们会将经常看到计算 id,然后检查 id 是否存在对应市场的操作,后文再次出现时将不再赘述。
用户存款时可以选择存入固定数量的资产( assets 参数)或者存入固定数量的 share( shares 参数)。 UtilsLib.exactlyOneZero 就是用来判断两个参数是否一个不为零值,另一个被置为零值。比如用户希望存入一定数量的资产,该用户可以将 assets 置为存入资产的数量,而 shares 直接置为零。 UtilsLib.exactlyOneZero 函数的源代码如下:
function exactlyOneZero(uint256 x, uint256 y) internal pure returns (bool z) {
assembly {
z := xor(iszero(x), iszero(y))
}
}
onBehalf 参数设计上代表用户希望将资产存给哪一个地址,在 Morpho Bule 内,用户可以直接将资产存入给其他地址。而 data 则用于回调 onBehalf 的 onMorphoSupply 函数。
接下来, supply 函数会将用户输入的 asset 或者 share 转化为 share 或者 asset。代码如下:
if (assets > 0) shares = assets.toSharesDown(market[id].totalSupplyAssets, market[id].totalSupplyShares);
else assets = shares.toAssetsUp(market[id].totalSupplyAssets, market[id].totalSupplyShares);
作为协议开发者,我们需要将所有的误差转移给用户。所以在 assets 转化为 shares 的过程中,我们选择 toSharesDown 函数来避免用户获得更多的 shares。而在 shares 转化为 assets 过程中,我们选择使用 toAssetsUp 函数,以此获得更多的 assets,但这并不会给用户带来好处,因为无论是用户获取利息还是最终提款,我们都是使用 share 作为用户的核心指标。而 assets 增加会导致后期计算 market[id].totalSupplyAssets += assets.toUint128(); 时, totalSupplyAssets 变大,进一步导致之后调用 supply 的用户获得更少的 share ,承担误差损失。
当完成上述所有操作后,接下来, supply 函数会更新一系列的存储变量,最后将用户资产转移到金库内部。
而提款操作使用 withdraw 函数与 supply 函数基本一致。我们主要介绍一些不一致的地方。首先, withdraw 函数也要求用户输入 onBehalf 参数,该参数的含义为提取哪一个地址的存款,但同时 withdraw 函数还要求用户输入 receiver 参数,该参数用于取出资产的最终目的地。所以不同于 supply 函数, withdraw 函数内部在校验 marketParams \ assets \ shares 之外,还校验了 onBehalf 和 msg.sender 之间的关系。
require(_isSenderAuthorized(onBehalf), ErrorsLib.UNAUTHORIZED);
此处使用的 _isSenderAuthorized 函数的定义如下:
function _isSenderAuthorized(address onBehalf) internal view returns (bool) {
return msg.sender == onBehalf || isAuthorized[onBehalf][msg.sender];
}
用户可以使用 setAuthorization 和 setAuthorizationWithSig 函数修改 isAuthorized 内的授权关系。
function setAuthorization(address authorized, bool newIsAuthorized) external {
require(newIsAuthorized != isAuthorized[msg.sender][authorized], ErrorsLib.ALREADY_SET);
isAuthorized[msg.sender][authorized] = newIsAuthorized;
emit EventsLib.SetAuthorization(msg.sender, msg.sender, authorized, newIsAuthorized);
}
上述 setAuthorization 类似 ERC20 代币内的 approve 操作,将自己的 Morpho Bule 仓位授权给其他用户。而 setAuthorizationWithSig 则类似 ERC20 代币内的 permit 操作,使用自己的签名将仓位授权给其他用户:
function setAuthorizationWithSig(Authorization memory authorization, Signature calldata signature) external {
/// Do not check whether authorization is already set because the nonce increment is a desired side effect.
require(block.timestamp <= authorization.deadline, ErrorsLib.SIGNATURE_EXPIRED);
require(authorization.nonce == nonce[authorization.authorizer]++, ErrorsLib.INVALID_NONCE);
bytes32 hashStruct = keccak256(abi.encode(AUTHORIZATION_TYPEHASH, authorization));
bytes32 digest = keccak256(bytes.concat("\x19\x01", DOMAIN_SEPARATOR, hashStruct));
address signatory = ecrecover(digest, signature.v, signature.r, signature.s);
require(signatory != address(0) && authorization.authorizer == signatory, ErrorsLib.INVALID_SIGNATURE);
emit EventsLib.IncrementNonce(msg.sender, authorization.authorizer, authorization.nonce);
isAuthorized[authorization.authorizer][authorization.authorized] = authorization.isAuthorized;
emit EventsLib.SetAuthorization(
msg.sender, authorization.authorizer, authorization.authorized, authorization.isAuthorized
);
}
上述代码实际上完成了 EIP712 的签名校验。EIP721 签名的结构体就是 Authorization 结构体,该结构体的定义如下:
struct Authorization {
address authorizer;
address authorized;
bool isAuthorized;
uint256 nonce;
uint256 deadline;
}
其中 authorizer 是授权人,而 authorized 是被授权人。上述对于 EIP712 的签名校验流程可以具体参考笔者之前的 EIP712 介绍。
重新回到 withdraw 函数,当 withdraw 函数校验完成 onBehalf 和 msg.sender 的授权关系后, withdraw 函数会使用 _accrueInterest 函数完成利率计算。由此保证用户可以拿到所有的利息。然后, withdraw 函数会计算 assets 和 shares。在此处也涉及到使用向上取整函数还是向下取整函数的问题。记住我们的原则,一切误差由用户承担。所以在 assets 转化为 shares 的过程中,我们会使用 toSharesUp 函数,以此将误差损失叠加到用户已有的 shares 内部。而将 shares 转化为 assets 的过程中,我们会使用 toAssetsDown 函数,以此将误差叠加到用户提取的资产中。之后我们将更新存储变量:
position[id][onBehalf].supplyShares -= shares;
market[id].totalSupplyShares -= shares.toUint128();
market[id].totalSupplyAssets -= assets.toUint128();
在提取用户的资产前,我们会使用 require(market[id].totalBorrowAssets <= market[id].totalSupplyAssets, ErrorsLib.INSUFFICIENT_LIQUIDITY); 保证借贷金库不会出现亏空。最后释放事件并将资产从金库内部转移给用户。
存入和提取担保品
与其他借贷协议不同,Moprho Bule 完全分隔了担保品和存入资产的概念。用户使用 supply 函数存入的资金并不能用作担保品。担保品的管理使用了另一套函数,其中存入担保品需要调用 supplyCollateral 函数,而提取担保品则需要调用 withdrawCollateral 函数。
由于担保品不并记录利息,所以此处也没有使用 share 方案为担保品进行计息操作,而是直接在内部使用 Position 中的 collateral 字段记录了用户已存入的担保品数量。
struct Position {
uint256 supplyShares;
uint128 borrowShares;
uint128 collateral;
}
存入担保品的方法非常简单,如下:
function supplyCollateral(MarketParams memory marketParams, uint256 assets, address onBehalf, bytes calldata data)
external
{
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(assets != 0, ErrorsLib.ZERO_ASSETS);
require(onBehalf != address(0), ErrorsLib.ZERO_ADDRESS);
// Don't accrue interest because it's not required and it saves gas.
position[id][onBehalf].collateral += assets.toUint128();
emit EventsLib.SupplyCollateral(id, msg.sender, onBehalf, assets);
if (data.length > 0) IMorphoSupplyCollateralCallback(msg.sender).onMorphoSupplyCollateral(assets, data);
IERC20(marketParams.collateralToken).safeTransferFrom(msg.sender, address(this), assets);
}
由于担保品与利息实际没有关系,所以在 supplyCollateral 并没有调用利息更新函数。提取担保品则复杂一些,因为担保品的提取涉及到借贷仓位健康度的计算。我们首先介绍用于借贷仓位健康度计算 _isHealthy 函数。该函数较为简单,代码如下:
function _isHealthy(MarketParams memory marketParams, Id id, address borrower) internal view returns (bool) {
if (position[id][borrower].borrowShares == 0) return true;
uint256 collateralPrice = IOracle(marketParams.oracle).price();
return _isHealthy(marketParams, id, borrower, collateralPrice);
}
function _isHealthy(MarketParams memory marketParams, Id id, address borrower, uint256 collateralPrice)
internal
view
returns (bool)
{
uint256 borrowed = uint256(position[id][borrower].borrowShares).toAssetsUp(
market[id].totalBorrowAssets, market[id].totalBorrowShares
);
uint256 maxBorrow = uint256(position[id][borrower].collateral).mulDivDown(collateralPrice, ORACLE_PRICE_SCALE)
.wMulDown(marketParams.lltv);
return maxBorrow >= borrowed;
}
我们首先调用预言机合约的 price 函数获得担保品兑换借出资产的比值。然后在 _isHealthy 函数内部先将用户的借出的 share 转化为借出资产的数量,然后使用 price 与 position[id][borrower].collateral 计算出用户可以借出的最大资产数量。最后将最大借出资产的数量与已借出资产数量比较即可。
注意这里依旧保持了一切误差由用户承担的基本原则,在计算 borrowed 的时候使用了 toAssetsUp 函数来最大化用户借出资产,而在计算 maxBorrow 时,则使用了 mulDivDown 和 wMulDown 函数,来最小化用户最大可借出资产。
withdrawCollateral 函数也比较简单,其代码如下:
function withdrawCollateral(MarketParams memory marketParams, uint256 assets, address onBehalf, address receiver)
external
{
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(assets != 0, ErrorsLib.ZERO_ASSETS);
require(receiver != address(0), ErrorsLib.ZERO_ADDRESS);
require(_isSenderAuthorized(onBehalf), ErrorsLib.UNAUTHORIZED);
_accrueInterest(marketParams, id);
position[id][onBehalf].collateral -= assets.toUint128();
require(_isHealthy(marketParams, id, onBehalf), ErrorsLib.INSUFFICIENT_COLLATERAL);
emit EventsLib.WithdrawCollateral(id, msg.sender, onBehalf, receiver, assets);
IERC20(marketParams.collateralToken).safeTransfer(receiver, assets);
}
由于 withdrawCollateral 在判断用户仓位是否健康时会使用到利息,所以在 withdrawCollateral 函数内部包含 _accrueInterest 函数来更新仓位的利息。在函数的最后,使用了 _isHealthy 函数判断用户仓位是否健康。
借款和偿还借款
借款和偿还借款与 withdrawCollateral 是有一定相似之处的。 borrow 的代码如下:
function borrow(
MarketParams memory marketParams,
uint256 assets,
uint256 shares,
address onBehalf,
address receiver
) external returns (uint256, uint256) {
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(UtilsLib.exactlyOneZero(assets, shares), ErrorsLib.INCONSISTENT_INPUT);
require(receiver != address(0), ErrorsLib.ZERO_ADDRESS);
require(_isSenderAuthorized(onBehalf), ErrorsLib.UNAUTHORIZED);
_accrueInterest(marketParams, id);
if (assets > 0) shares = assets.toSharesUp(market[id].totalBorrowAssets, market[id].totalBorrowShares);
else assets = shares.toAssetsDown(market[id].totalBorrowAssets, market[id].totalBorrowShares);
position[id][onBehalf].borrowShares += shares.toUint128();
market[id].totalBorrowShares += shares.toUint128();
market[id].totalBorrowAssets += assets.toUint128();
require(_isHealthy(marketParams, id, onBehalf), ErrorsLib.INSUFFICIENT_COLLATERAL);
require(market[id].totalBorrowAssets <= market[id].totalSupplyAssets, ErrorsLib.INSUFFICIENT_LIQUIDITY);
emit EventsLib.Borrow(id, msg.sender, onBehalf, receiver, assets, shares);
IERC20(marketParams.loanToken).safeTransfer(receiver, assets);
return (assets, shares);
}
由于借贷会直接影响利率,所以 borrow 和 repay 内部都包含 _accrueInterest 函数以更新利率。然后计算 shares 和 assets,依旧使用的是误差留给用户的原则。将用户借出的资产 assets 使用 toAssetsDown 来降低,而对用户借款的 shares 则使用 toSharesUp 变多,这样后期用户偿还借款时会偿还更多资产。
在完成了变量更新后, borrow 函数调用 _isHealthy 函数来判断用户当前担保品是否可以支持资产借出。最后将资产转移给用户就完成了资产的借出。
对于还款而言,用户需要调用 repay 函数。 repay 函数的代码如下:
function repay(
MarketParams memory marketParams,
uint256 assets,
uint256 shares,
address onBehalf,
bytes calldata data
) external returns (uint256, uint256) {
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(UtilsLib.exactlyOneZero(assets, shares), ErrorsLib.INCONSISTENT_INPUT);
require(onBehalf != address(0), ErrorsLib.ZERO_ADDRESS);
_accrueInterest(marketParams, id);
if (assets > 0) shares = assets.toSharesDown(market[id].totalBorrowAssets, market[id].totalBorrowShares);
else assets = shares.toAssetsUp(market[id].totalBorrowAssets, market[id].totalBorrowShares);
position[id][onBehalf].borrowShares -= shares.toUint128();
market[id].totalBorrowShares -= shares.toUint128();
market[id].totalBorrowAssets = UtilsLib.zeroFloorSub(market[id].totalBorrowAssets, assets).toUint128();
// `assets` may be greater than `totalBorrowAssets` by 1.
emit EventsLib.Repay(id, msg.sender, onBehalf, assets, shares);
if (data.length > 0) IMorphoRepayCallback(msg.sender).onMorphoRepay(assets, data);
IERC20(marketParams.loanToken).safeTransferFrom(msg.sender, address(this), assets);
return (assets, shares);
}
其中大部分逻辑都较为简单。唯一见过的逻辑是 UtilsLib.zeroFloorSub 函数,该函数的实现如下:
/// @dev Returns max(0, x - y).
function zeroFloorSub(uint256 x, uint256 y) internal pure returns (uint256 z) {
assembly {
z := mul(gt(x, y), sub(x, y))
}
}
其他逻辑都较为简单。
清算借贷仓位
清算是一个较为复杂的操作, liquidate 函数是目前代码行数最多的函数。我们首先观察该函数的参数定义:
function liquidate(
MarketParams memory marketParams,
address borrower,
uint256 seizedAssets,
uint256 repaidShares,
bytes calldata data
) external returns (uint256, uint256) {}
此处较为特殊的参数 seizedAssets 和 repaidShares,和之前介绍的函数类似,用户只能传递两个参数中的一个并把另一个置为零值。 seizedAssets 的含义为清算者希望在此处清算中获得用户担保品的数量,而 repaidShares 的含义为清算者希望偿还的用户负债 share 的数量。
liquidate 函数的第一部分就是输入参数的校验和利息的累积:
Id id = marketParams.id();
require(market[id].lastUpdate != 0, ErrorsLib.MARKET_NOT_CREATED);
require(UtilsLib.exactlyOneZero(seizedAssets, repaidShares), ErrorsLib.INCONSISTENT_INPUT);
_accrueInterest(marketParams, id);
在 liquidate 函数的第二部分,我们将计算 seizedAssets 和 repaidShares 中的一方。这里需要注意,正如我们在本文最开始时介绍的,清算是存在激励因子的。该部分对应的代码如下:
{
uint256 collateralPrice = IOracle(marketParams.oracle).price();
require(!_isHealthy(marketParams, id, borrower, collateralPrice), ErrorsLib.HEALTHY_POSITION);
// The liquidation incentive factor is min(maxLiquidationIncentiveFactor, 1/(1 - cursor*(1 - lltv))).
uint256 liquidationIncentiveFactor = UtilsLib.min(
MAX_LIQUIDATION_INCENTIVE_FACTOR,
WAD.wDivDown(WAD - LIQUIDATION_CURSOR.wMulDown(WAD - marketParams.lltv))
);
if (seizedAssets > 0) {
uint256 seizedAssetsQuoted = seizedAssets.mulDivUp(collateralPrice, ORACLE_PRICE_SCALE);
repaidShares = seizedAssetsQuoted.wDivUp(liquidationIncentiveFactor).toSharesUp(
market[id].totalBorrowAssets, market[id].totalBorrowShares
);
} else {
seizedAssets = repaidShares.toAssetsDown(market[id].totalBorrowAssets, market[id].totalBorrowShares)
.wMulDown(liquidationIncentiveFactor).mulDivDown(ORACLE_PRICE_SCALE, collateralPrice);
}
}
我们首先从预言机内部获取当前担保品的价格,然后使用 _isHealthy 函数计算当前仓位是否可被清算。之后,我们将计算清算激励因子(LIF)。最后,我们根据用户输入的参数来计算另一个参数。假如用户输入的是 seizedAssets,这代表清算者希望获得 seizedAssets 单位的担保品。我们首先使用 seizedAssets.mulDivUp(collateralPrice, ORACLE_PRICE_SCALE) 获得担保品对应的负债数量。然后将负债数量除以 LIF 获得真正可清算的负债数量,然后将其转化为 shares。上述流程的具体原理可以参考以下公式:
$$ SeizableAssets = debtAmount ∗ LIF $$
即清算者获得的担保品价值应该是清算债务价值与 LIF 的乘积。反之,已知可获得的担保品数量,那么就可以通过除以 LIF 反向推导出可清算资产的数量。
假如用户输入的是 repaidShares,即用户希望清算的负债份额,那么只需要使用 toAssetsDown 将其转化为清算负债的数量,然后与 LIF 相乘获得获得担保品的数量,最后与预言机返回的结果相除即可。
在 liquidate 函数的第三部分,我们主要进行存储变量的更新:
uint256 repaidAssets = repaidShares.toAssetsUp(market[id].totalBorrowAssets, market[id].totalBorrowShares);
position[id][borrower].borrowShares -= repaidShares.toUint128();
market[id].totalBorrowShares -= repaidShares.toUint128();
market[id].totalBorrowAssets = UtilsLib.zeroFloorSub(market[id].totalBorrowAssets, repaidAssets).toUint128();
position[id][borrower].collateral -= seizedAssets.toUint128();
我们将用户仓位的 borrowShares 减去清算的份额。在市场的总借出的份额和资产内减去偿还的份额和资产。最后减去用户的保证金。
在 liquidate 函数的第四部分内,我们主要处理可能的坏账。所谓的坏账指即使用户的保证金已经归零,但仍存在借贷仓位:
uint256 badDebtShares;
uint256 badDebtAssets;
if (position[id][borrower].collateral == 0) {
badDebtShares = position[id][borrower].borrowShares;
badDebtAssets = UtilsLib.min(
market[id].totalBorrowAssets,
badDebtShares.toAssetsUp(market[id].totalBorrowAssets, market[id].totalBorrowShares)
);
market[id].totalBorrowAssets -= badDebtAssets.toUint128();
market[id].totalSupplyAssets -= badDebtAssets.toUint128();
market[id].totalBorrowShares -= badDebtShares.toUint128();
position[id][borrower].borrowShares = 0;
}
主要在 position[id][borrower].collateral == 0 的情况下做最终清算。
在 liquidate 函数的第五部分内,我们最终完成资产的划转与事件释放。
emit EventsLib.Liquidate(
id, msg.sender, borrower, repaidAssets, repaidShares, seizedAssets, badDebtAssets, badDebtShares
);
IERC20(marketParams.collateralToken).safeTransfer(msg.sender, seizedAssets);
if (data.length > 0) IMorphoLiquidateCallback(msg.sender).onMorphoLiquidate(repaidAssets, data);
IERC20(marketParams.loanToken).safeTransferFrom(msg.sender, address(this), repaidAssets);
return (seizedAssets, repaidAssets);
闪电贷
在本章节的最后部分,我们介绍闪电贷的部分内容。Morpho Bule 的闪电贷函数实现非常简单:
function flashLoan(address token, uint256 assets, bytes calldata data) external {
require(assets != 0, ErrorsLib.ZERO_ASSETS);
emit EventsLib.FlashLoan(msg.sender, token, assets);
IERC20(token).safeTransfer(msg.sender, assets);
IMorphoFlashLoanCallback(msg.sender).onMorphoFlashLoan(assets, data);
IERC20(token).safeTransferFrom(msg.sender, address(this), assets);
}
甚至都没有闪电贷的手续费计算。
IRM 实现
在本文最开始介绍利率是就非常详细介绍了 Morpho Bule 目前使用的 AdaptiveCurveIrm 利率模型。在本节内,我们将详细介绍该利率模型的具体实现。该利率模型的源代码位于 morpho-blue-irm 内,我们主要介绍的代码都位于 src/adaptive-curve-irm/AdaptiveCurveIrm.sol 文件内部。
AdaptiveCurveIrm 的核心函数就是 borrowRate 函数,该函数的实现非常简单:
function borrowRate(MarketParams memory marketParams, Market memory market) external returns (uint256) {
require(msg.sender == MORPHO, ErrorsLib.NOT_MORPHO);
Id id = marketParams.id();
(uint256 avgRate, int256 endRateAtTarget) = _borrowRate(id, market);
rateAtTarget[id] = endRateAtTarget;
// Safe "unchecked" cast because endRateAtTarget >= 0.
emit BorrowRateUpdate(id, avgRate, uint256(endRateAtTarget));
return avgRate;
}
首先,对于传入参数而言, borrowRate 函数要求调用者直接传入 MarketParams 和 Market 结构体。这两个结构体已在上文有所介绍。然后调用 _borrowRate 函数,该函数会返回 avgRate 和 endRateAtTarget 两个利率。其中 avgRate 将会被返回给 Morpho Bule 合约用于利率计算,而 rateAtTarget 则将存储在合约内部,用于下一步利率计算,即作为 $R_{i-1}$。
故而此处的核心函数为 _borrowRate 内部函数。该函数的实现较为复杂。在 _borrowRate 函数内部,我们首先计算当前市场的 $e(u)$ 参数。在此处,我们再次给出 $e(u)$ 的计算公式:
$$
e(u) = \begin{cases}
\frac{u(t) - u{target}}{1 - u{traget}} &\text{if } u(t) > u{target} \
\frac{u(t) - u{target}}{u{traget}} &\text{if } u(t) \le u{target}
\end{cases}
$$
上述计算公式在 _borrowRate 内部的实现如下:
int256 utilization =
int256(market.totalSupplyAssets > 0 ? market.totalBorrowAssets.wDivDown(market.totalSupplyAssets) : 0);
int256 errNormFactor = utilization > ConstantsLib.TARGET_UTILIZATION
? WAD - ConstantsLib.TARGET_UTILIZATION
: ConstantsLib.TARGET_UTILIZATION;
int256 err = (utilization - ConstantsLib.TARGET_UTILIZATION).wDivToZero(errNormFactor);
我们首先计算利用率 utilization。然后更具公式计算 $e(u)$。此处的 TARGET_UTILIZATION 就是 $e(u)$ 计算公式内的 $u_{target}$。此处先计算了 errNormFactor ,即分母部分,然后计算了 err。
在 _borrowRate 函数的第二部分,我们将真正进入利率计算。我们根据情况初始化利率:
int256 startRateAtTarget = rateAtTarget[id];
int256 avgRateAtTarget;
int256 endRateAtTarget;
if (startRateAtTarget == 0) {
// First interaction.
avgRateAtTarget = ConstantsLib.INITIAL_RATE_AT_TARGET;
endRateAtTarget = ConstantsLib.INITIAL_RATE_AT_TARGET;
} else {
...
}
上述部分代码会在 startRateAtTarget 即利率曲线第一次执行时初始化基础利率。而 else 内部就会执行常规的利率计算。我们在此处再次给出利率的计算公式:
$$
ri = \text{curve}(e(u)) * R{i-1}\text{speed}(u)
$$
此时,我们已有 $e(u)$ 的数值,只需要计算其他参数即可。我们第一步主要计算 $\text{speed}(u)$。计算的数学公式如下:
$$
\text{speed}(u) = \exp\left(u(t)\cdot\frac{50 \times \Delta_t}{31556926}\right)
$$
在 _borrowRate 内部,实现代码如下:
int256 speed = ConstantsLib.ADJUSTMENT_SPEED.wMulToZero(err);
int256 elapsed = int256(block.timestamp - market.lastUpdate);
int256 linearAdaptation = speed * elapsed;
上述的 linearAdaptation 实际上对应 $\frac{50 \times \Delta_t}{31556926}$。此处的 ConstantsLib.ADJUSTMENT_SPEED = 50 ether / int256(365 days);。
接下来,我们会使用 linearAdaptation 进行进一步的利率计算,但首先存在 linearAdaptation = 0 的可能性。比如在同一个区块内两次调用到需要利率更新的函数时就会出现 elapsed = 0 ,进而导致 linearAdaptation = 0。对于 linearAdaptation = 0 的情况,我们不需要进一步利率计算,直接返回上一次的计算结果即可。
if (linearAdaptation == 0) {
// If linearAdaptation == 0, avgRateAtTarget = endRateAtTarget = startRateAtTarget;
avgRateAtTarget = startRateAtTarget;
endRateAtTarget = startRateAtTarget;
} else { ... }
此处的 startRateAtTarget 就是上一次的计算结果。当 linearAdaptation != 0 时,我们将执行以下代码:
endRateAtTarget = _newRateAtTarget(startRateAtTarget, linearAdaptation);
int256 midRateAtTarget = _newRateAtTarget(startRateAtTarget, linearAdaptation / 2);
avgRateAtTarget = (startRateAtTarget + endRateAtTarget + 2 * midRateAtTarget) / 4;
上述代码内使用了 _newRateAtTraget 函数,该函数定义如下:
function _newRateAtTarget(int256 startRateAtTarget, int256 linearAdaptation) private pure returns (int256) {
// Non negative because MIN_RATE_AT_TARGET > 0.
return startRateAtTarget.wMulToZero(ExpLib.wExp(linearAdaptation)).bound(
ConstantsLib.MIN_RATE_AT_TARGET, ConstantsLib.MAX_RATE_AT_TARGET
);
}
该函数实际上完成了 $R_{i-1}{\text{speed}(u)}$ 的最终计算。在上文内,我们曾提及在真实情况下,我们应该使用以下代码进行利率计算:
$$ ri = \text{curve}(e(u)) * R{i - 1} * \frac{\int^{\Delta_t}_0\text{speed}(u)}{\Delta_t} $$
所以此处需要计算 $r_{i-1} * \int^{\Delta_t}_0\text{speed}(u)$ 的结果。此处 Morpho Bule 团队使用了 Trapezoidal rule 来计算。该方法是用来近似求解积分结果的,如下:
$$ \displaystyle \int {a}^{b}f(x),dx\approx \sum {k=1}^{N}{\frac {f(x{k-1})+f(x{k})}{2}}\Delta x_{k} $$
设此处的 $N = 2$,那么结果为:
$$ \displaystyle \int _{a}^{b}f(x),dx\approx \frac{\Deltat}{2}(x{start} + 2 \times x{mid} + x{end}) $$
此处的 $\Deltat = t / 2$,所以上述公式可以进一步推导为 $\frac{t}{4}(x{start} + 2 \times x{mid} + x{end})$。注意,我们希望计算最终的平均值,所以此处还需要将 $t$ 时间除掉,所以最终结果为 $(x{start} + 2 \times x{mid} + x_{end}) / 4$。这就是 avgRateAtTarget = (startRateAtTarget + endRateAtTarget + 2 * midRateAtTarget) / 4; 的由来。
在完成上述最终计算后, endRateAtTarget 可以将其写入存储以便于下次计算。所以在上文内我们描述的利率模型是存在一定问题的,$r_{i - 1}$ 实际上并不是最终完全利用公式计算出的结果。
最后,我们可以计算一下最终用于计算利息的利率。代码如下:
return (uint256(_curve(avgRateAtTarget, err)), endRateAtTarget);
在计算过程中使用了 _curve 函数,该函数定义如下:
function _curve(int256 _rateAtTarget, int256 err) private pure returns (int256) {
// Non negative because 1 - 1/C >= 0, C - 1 >= 0.
int256 coeff = err < 0 ? WAD - WAD.wDivToZero(ConstantsLib.CURVE_STEEPNESS) : ConstantsLib.CURVE_STEEPNESS - WAD;
// Non negative if _rateAtTarget >= 0 because if err < 0, coeff <= 1.
return (coeff.wMulToZero(err) + WAD).wMulToZero(int256(_rateAtTarget));
}
上述代码的核心是实现了如下数学函数:
$$
\text{curve}(u) =\begin{cases}
(kd - 1) * e(u) + 1 &\text{if } u(t) > u{target} \
(1 - kd) * e(u) + 1 &\text{if } u(t) \le u{target}
\end{cases}
$$
并最终使用上述计算获得的 $\text{curve}(u)$ 对 avgRateAtTarget 进行调整。
总结
本文主要介绍了 Morpho Bule 的核心部分,包含:
- 清算规则和利率计算
- 预言机实现
- Morpho Bule 的核心代码和 IRM 部分代码
本文没有介绍 Morpho Bule 所使用的其他组件库,读者可以自行阅读。相比于其他借贷协议,Morpho Bule 的核心代码简单造成的后果是担保品并不能获得利息,且不允许多个担保品同时抵押借贷同一个资产。这实际上相当弱化了其借贷属性,笔者认为 Morpho Bule 实际上是一个依附于利率衍生品的特化借贷协议。
在目前来看,Morpho Bule 内部大型的借贷金库都选择使用自带利率的资产,如 wstETH 作为担保品,而另一侧借出资产往往是稳定币等。对于一般的借贷业务,即担保品没有原生利率的资产,则不适合发行在 Morpho Bule。
- 第一 DeFi 协议 - Aave 893 浏览
- 第6章:去中心化借贷 1718 浏览
- 深入浅出借贷市场内的 Pendle 预言机 419 浏览
- DeFi顶级货币市场的核心架构与定位 925 浏览
- 预言机基础设施:借贷协议的支柱 690 浏览
- DeFi Mullet 的先锋:Coinbase 在前,DeFi 在后 689 浏览
- Euler 和 Morpho 的高层次比较 2211 浏览
- Morpho Blue 白皮书翻译 5643 浏览
- 处理借贷协议中的利用率 1375 浏览
- 评估无许可借贷领域 1541 浏览

