HyperPlonk，一种专为ZKEVM设计的零知识证明系统

作者：Binyi Chen 和 Benedikt Bünz

论文：https://eprint.iacr.org/2022/1355

零知识证明系统是区块链隐私和可扩展性的核心构建块。这些系统允许证明者向验证者证明某个状态转换是正确的。这可以是一个 CAPE 交易或许多交易的汇总。零知识证明（又名 zk-SNARKs）的两个重要特性是： (i) 证明不会泄露关于状态转换的任何信息，除了它是有效的；和 (ii) 证明是简短的且高效检查，即使状态转换很复杂且涉及许多交易。

在过去的几年中，Plonk 已成为区块链领域大多数应用的首选证明系统。原因在于 Plonk 提供了短证明、高效验证、高度自定义和最小信任假设之间的优秀权衡。不幸的是，Plonk 仍然存在限制，特别是在证明大型陈述或尝试使用高度并行的硬件时。这些限制在证明大型和复杂操作（如 rollups 和 zkEVMs）时尤其重要。

为了克服这些瓶颈，我们构建了 Hyperplonk。一个新的 zk-proof 系统，具有完全线性的证明者和对高阶和查找自定义门的支持。我们原型实现的 Hyperplonk 已经在约 16000 个约束的电路中超越了我们高度优化的 Plonk 实现（Jellyfish），而且随着陈述大小的增加或更多并行性的使用，这一差距不断扩大。Hyperplonk 还支持高阶自定义门和查找，这对于复杂电路（如 ZK-EVM 电路）特别有用。这些特殊门可以用于启用复杂的 EVM OPCODES 和构建内存堆栈。

Plonk：背景和限制

现代证明系统由两个关键构建块构成。一个信息理论多项式交互oracle证明（PIOP），将计算转化为多项式方程。而用于证明方程获取满足的多项式承诺方案。示例 PIOP 包括 Plonk、Marlin 和 Spartan。多项式承诺方案的示例有 KZG、Bulletproofs、Virgo（FRI）和 DARK ¹。

这种分割的好处在于你可以结合任何 PIOP 和任何多项式承诺方案，以获得新的特性。例如， Halo2 将 PLONK PIOP 与 Bulletproofs 多项式承诺结合起来。Plonky2 将 PLONK 与基于 FRI 的多项式承诺结合。Xiphos 将 Quarks（对 Spartan PIOP 的改进）与 Dory 结合使用，等等。

PLONK PIOP 受到了业界的广泛关注。一个主要原因是，与其他证明系统不同，它支持自定义门。传统的证明系统要求你将计算表述为加法和乘法，而 PLONK 则支持不同的门，例如 X³*Y+Y+X=Z。在我们最近关于 VERI-ZEXE 的工作中，我们展示了这些门可以显著减少证明者的运行时间。此外，PLONK（和 Plookup）支持一种称为查找的功能。这使得可以高效地证明某个值在某个表中。例如，如果表中包含数字 [0,...,2³²-1]，则可以高效地表示某个值是一个 32 位数字。正因如此，构建 ZKEVM 的所有努力都是使用 PLONK 或类似 PLONK 的系统²。但到目前为止，这些系统仍有一个主要缺点。

作为第一步，PLONK 需要你将电路值编码为多项式。如图所示，我们将电路写成一个表格，然后构建一个多项式，使其在一组点上等于这些值。找到这个多项式是通过所谓的快速傅立叶变换（FFT）完成的。

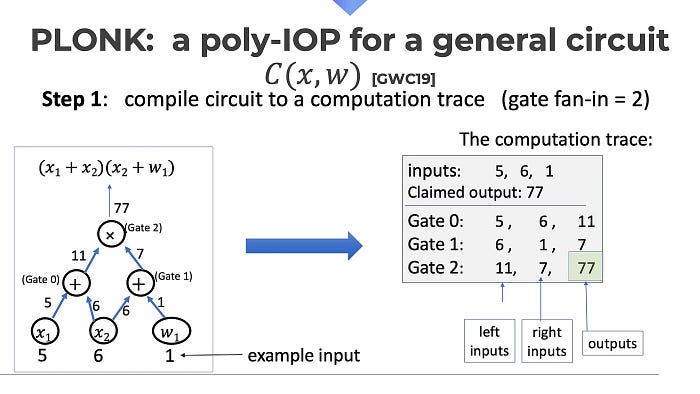
将一个计算写成电路，然后将计算的轨迹写成一个表格

将轨迹编码为多项式。这需要 FFT，Hyperplonk 的目标是消除这个昂贵的步骤。

FFT 是美妙的算法[见这里]，但不幸的是，它们仍然有显著的开销。FFT 的运行时间与电路大小 n 成正比，为 n log₂(n)。当 n 较小或中等时，这并不会构成挑战，但当 n 大于约一百万（且 log₂(n) 约为 20）时，FFT 成为一个重要因素。这在 zk-rollups 和 zkEVMs 等系统中尤其成问题，因为电路可能有近十亿个门。其中一个额外的瓶颈是这些 FFT 的并行化效果不佳，并且需要复杂的内存访问。因此，所有这些限制了对零知识证明的新型硬件（例如 GPUs、FPGAs 和 ASICs）的部署和实用性。

通过多元法去除 FFT

Hyperplonk 的目标是从 Plonk 中移除对 FFT 的要求，使其更具可扩展性并更适合于定制硬件。为此，我们依赖一些在 90 年代早期的证明系统中使用的旧技巧 [ Sumcheck、GKR、Hyrax、Spartan、Quarks……]。我们不再使用一个变量来编码多项式 P(X)，而是使用多个变量（确切地说是 log₂(n)），编码一个多项式 P(X₁,X₂,...,Xμ)。结果证明，对于 log₂(n) 个变量，我们能够找到一个编码 n 个值的多项式，但它在每个变量上最多是线性的。这意味着，这个多项式没有 Xi² 的项。例如，我们可以轻松在时间 n 内编码一个所谓的多线性多项式，该多项式在值 (0,0,…0)到 (1,1,…,1) 取值。这个称为布尔超立方体，因为每个变量要么取值 0，要么取值 1，正如你可能猜到的，这个超立方体激发了 HyperPlonk 的名称。

与标准 Plonk 不同，HyperPlonk 通过多个变量将计算轨迹编码为多线性多项式。

构建多线性多项式的工具箱

高效地将值编码为多线性多项式消除了对 FFT 的需求，但这仅是一个起点。Plonk 可以被描述为一组子协议，这些协议被调用以构建大协议。这些协议包括用于门检查的电路，确保电路中的每个门都满足。例如，如果乘法门的输入为 7 和 11，则输出必须为 77。另一个协议是所谓的接线或置换检查。该协议确保电路正确连接，并且一个门的输出是下一个门的正确输入。例如，我们希望确保门 1 的输出等于门 2 的正确输入。在 Plonk 中，这些协议是通过单变量多项式构建的（而且许多还需要额外的 FFT）。我们需要适应并构建可用于多线性多项式且不依赖于 FFT 的检查协议。为此，我们构建了一套多线性多项式的子协议工具箱。其中一些是新的（例如在多个点评估多个多项式的批量协议），而一些则是非常古老的，例如著名的 SumCheck 协议（我们为高阶门提供了改进）。

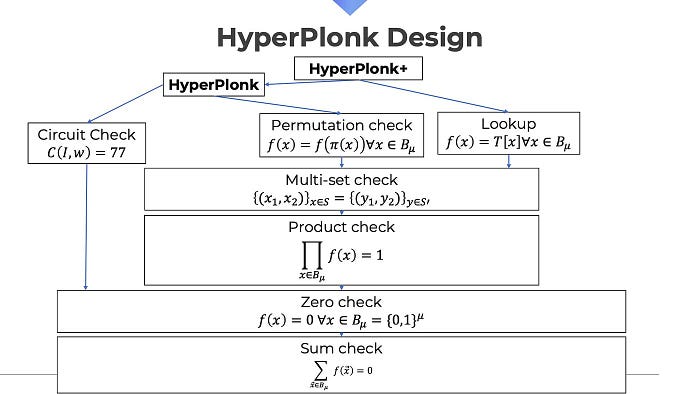
Hyperplonk 由许多子协议构成，并基于著名的 sumcheck 协议。

HyperPlonk、HyperPlonk+ 和自定义门

在这个工具箱到位之后，我们可以轻松构建 HyperPlonk。此项研究的一个关键目标是支持所有美好的 Plonk 特性与 Hyperplonk 执行。事实证明，我们可以做得更好。Plonk 支持自定义门，但存在一个权衡，即过大的（或更具体地说，高阶的）自定义门将增加所谓的商多项式的大小。这会减缓证明者的速度，并减少可能从较小电路中获得的收益。因此，在实践中使用的最大门阶为 5（例如 X⁵-Y=Z）。在 Hyperplonk 中，没有商多项式，对高阶门的权衡远优于 Plonk。我们评估显示，Hyperplonk 有潜力支持 32 阶门或更高，这对于某些计算可以显著改善证明者的时间。我们还支持查找，并将结合 HyperPlonk 和查找的协议称为 HyperPlonk+。我们相信，对高阶门和查找门的更好支持可以使 HyperPlonk 非常适合 zkEVM 应用。

附加：Orion+，一个超快速的多项式承诺方案

正如我们之前所述，现代证明系统包括一个 PIOP 和一个多项式承诺方案（PCS）。HyperPlonk 是一个 PIOP，还有许多有趣的多项式承诺方案可以与之结合使用（在我们的评估中，我们使用 KZG 的多线性变体）。一个最近且特别有趣的 PCS 被称为 Orion。Orion 拥有绝对最快的证明者，并且与 HyperPlonk 和 HyperPlonk+ 完全兼容。Orion 对百万个门的证明，生成仅需 3 秒。不幸的是，对于约 3000 万个门的电路，其证明也非常大，约为 ~5.5MB（KZG 证明在相同大小时约为 1KB）。我们通过构建 Orion+ 来调和此问题，将 Orion 的证明大小显著缩小至相同电路的 ~7KB。在设计上，Orion+ 实际上使用 HyperPlonk 及其承诺和证明特性。我们仍在评估 Orion+ 的实用性，但这是一个非常令人兴奋的方向，可能提供一个快速的证明者，并具有合理的证明大小。

实施与评估

我们有一个 HyperPlonk 的原型实现，并且将其与我们在 Espresso 构建的最先进的 Plonk 实现 Jellyfish 进行了比较。我们的初步结果已经展现了 Hyperplonk 的威力。从约 16000 个约束的电路开始，Hyperplonk 超越 Jellyfish，电路越大，差距越大。Hyperplonk 的证明比 Plonk 的证明稍大（约 6kb 对 1kb），但对于许多应用来说，这仍然可以接受，并且它们明显比任何不使用 FFT 的其他证明系统更小。

我们还看到 Hyperplonk 可以高效支持高阶门。32 阶门的成本仅比 2 阶门高出 20%。

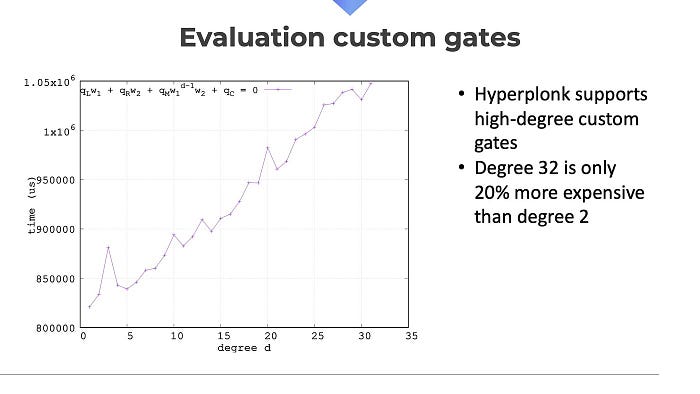
我们仍在对 HyperPlonk 的实现（及其潜在优化）进行研究。我们还计划在不久的将来将其集成到 Jellyfish 库中。

脚注

1. 一些系统（如 Bulletproofs）既是 PIOP 也是承诺方案。
2. Starkware 的 AIR 具有与 PLONK 非常相似的特性。

• 原文链接： medium.com/@espressosys/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～