密码学101：后量子密码学

这是关于密码学的一系列更大文章的一部分。如果这是你看到的第一篇文章，我强烈建议你从 系列的开头 开始。

现在基本的 环学习与错误 问题和理想格子理论已经涵盖，下一步就是将其充分利用。

在2016年，美国国家标准与技术研究院发起了一项名为 后量子密码学标准化项目 的倡议。这个想法是接收针对量子抗性算法的提名（稍后将对此进行更多介绍），希望挑选出最佳候选者并标准化一套可以用于构建下一代安全网络的技术。

经过几年后，四个赢家 被公布——其中三个是基于格的算法。

在这篇文章中，我们将看看这些算法是如何工作的，并讨论一下量子计算机如何威胁到确保我们日常通信的加密方法。

简要量子计算

我对 量子力学 领域不是专家（尽管我上过一两门相关课程）。凭借我有限的知识，我可以说这是一个相当复杂的话题，而且即使是理解一些最基本和最基础的概念也很具挑战性。这就是为什么我们不会深入讨论量子计算机的工作原理。然而，了解一下它的重要性仍是有必要的，以理解为什么我们需要担心它们的计算能力。

我们的日常计算机使用电流进行操作，电流本质上用于表示 二进制数字。你知道，电流流动表示 1，而不流动则表示 0——这被称为比特 。 每个位只能表示 两种状态。

此外，传统计算机中的操作是顺序执行的，意思是你需要读取一些数据位，执行一个操作（例如加法），存储结果数据……然后才能进行下一个操作。

这对人类来说运作得相当不错。计算机能够快速解决各种问题，这推动了许多知识领域的发展。

它们还给了我们《我的世界》。

但是，对于某些操作，这些简单的限制使得解决一些问题变得 绝对不可行。事实上，这就是密码学的目的：创造足够难以破解的难题，以至于我们当前的计算能力无法在合理时间内解决。

量子计算机的构建方式不同。信息的基本单位是 量子位，或者简称为 qubit。qubit 可以存在于既不是 0 也不是 1 的状态。它存在于多种状态的 叠加态 中，这意味着它是一种状态的组合。

一个可能的类比是振动的吉他弦。随着它的振动，它发出声音，因此它的“状态”对我们来说是非常真实的。但是我们如何数学地描述这种振动呢？实际上，我们可以将其描述为不同“简单”振动模式（称为振动模式）的组合。

这就是 叠加态 的本质：将当前状态表示为更简单部分的加权和。可能有 无限多个 部分，但这是可以接受的！

因为一个 qubit 编码的信息远远超过一个简单的 0 或 1，它能够同时执行多个操作。而且，这种能力随着我们拥有的 qubit 数量的增加而呈指数增长。

这个结果（结合一些我们甚至没有提到的奇怪术语，比如波函数塌缩和纠缠）就是更快的计算。如此之快，以至于我们当前基于椭圆曲线的方法几乎没有机会！

我们可以运行 Shor 算法 并快速破解诸如素因数分解问题的难题。

目前量子计算机并不太实用——你可能不久后能在任何地方看到这一篇文章。但我们无法预测未来的变化，即便量子计算机尚未成为日常使用的工具，专门设立其的设施也可能迅速破解复杂问题并破坏当前的安全模型。

总而言之：

当前的 ECC 方法可以被量子计算机破解，因此我们需要更好、更安全的算法。

这就是近期PQ密码学成为热门话题的主要原因：试图保护信息免受这潜在威胁。基于格子的难题被认为是如此困难，以至于甚至量子计算机也无法快速解决。

在这 Robustness 和 Security 的承诺下，让我们看看 NIST 提议的 两个 算法以进行标准化。但在那之前……

密钥生成

这两种算法将共享相同的私钥和公钥构造。这很像椭圆曲线密码学，其中密钥几乎总是一个大整数 d（私钥）和椭圆曲线中的点 [d]G（公钥）。

这次，密钥将涉及环，并基于我们已在上一篇文章中看到的 RLWE 问题 来确保安全。

好的，前言已经足够！让我们看看这如何运作。

就像你需要为任何 ECC 方法选择椭圆曲线一样（比如 ECDSA），我们这里也需要选择一个 ring，以及系统的一些 公共参数。

首先，我们选择环 R，通常的形式是：

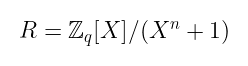
然后我们将从中抽取一组随机多项式。这些多项式将置于一个 k × l 矩阵中，称为 A：

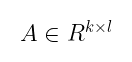
( R, A ) 这一对类似于 ( E, G ) ，其中 E 是一个椭圆曲线，G 是一个生成元。这里没有意外！

有了这一点，密钥生成就非常简单。我们需要一些私密信息用于私钥——这些将是两个多项式的向量，一个长度为 l，一个长度为 k。

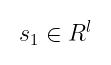
但是它们有一个特殊性——它们是 短多项式。在这个上下文中，"短" 是指每个多项式的向量表示，正如你可能回忆起的那样，使用 系数作为向量的坐标。

为了使向量“短”，我们需要系数比较小。因此，为了为这些 s₁ 和 s₂ 多项式进行取样，我们还要求系数很小，通常限制在范围 {−η, …,η} 内，其中 η 是一个小整数。

就像误差多项式或向量一样！

我们得到了私钥 (s₁, s₂)。我们只需计算：

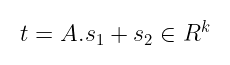
公钥将简单地是 (A, t)。注意，从 A 和 t 恢复 s₁ 和 s₂ 涉及解决 RLWE 问题——这意味着我们可以安全地共享公钥！

太好了！

非对称密钥，检查完毕。我们现在可以进入今天的内容。

Kyber

CRYSTALS Kyber 正式是一种 密钥封装机制（KEM），这意味着它是一种让发送者通过网络安全地传输简短秘密信息的方式——接收者然后能够恢复该秘密。

这与加密 相似，但通常用于不同的目的，如传输对称密钥，用于后续通信。

该技术由以下三个相当标准的步骤组成：密钥生成、封装（类似于加密）、和 解封装（相当于解密）。

幸运的是，我们知道密钥生成是如何工作的。接收方将生成一个公钥 (s₁, s₂)并与消息发送者共享相关的公钥 (A, t)。

有了这些，我们可以直接进入第二步。

封装

好的，这一过程大致上与你预期的加密工作方式相似：发送者希望与接收者共享一个值 M。但接下来发生的事情对我们来说可能听起来很奇特：他们将该值转换为其 二进制 表示——然后将数字编码为一个 多项式。更进一步，他们会将该多项式按字段大小一半的比例缩放，并进行四舍五入。

Excuse me?

是的，这可能有点难以理解。我觉得试着将其可视化会帮助我们理解这个过程，所以让我们继续一个玩具示例。

取数字 13。它的二进制表示为 1101。从右到左，如果我们将每个数字映射到 x 的 幂，那么我们最终得到的多项式为：

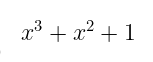
然后，假设我们在模 19 下工作。我们需要将这个多项式按 19 的一半的比例缩放，四舍五入后得到 10。所以，我们的值 13 被转换为：

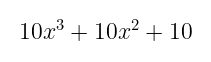
我知道，这显然不是我们习惯的——这一部分可能有点令人费解，但我 promise 它在短时间内会变得明晰。

因此，我们得到了多项式形式的消息——我们称之为 m。接下来，发送者需要计算密文 _。为此，他们抽取三个随机向量: r, e₁, 和 e₂，并执行这些操作：

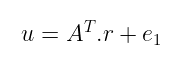
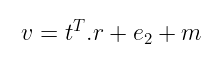
T 上标表示我们取一个向量或矩阵的 转置。

而结果密文就是 (u, v)。这将被发送给接收者，接收者接下来进行解封装。

请注意，我们可以在这里与 ECC 画出一些相似之处：r 是我们通常称之为的 随机数 ，我们需要一个值来编码随机数（u）和另一个值来编码消息及随机数（v）。**

解封装

最后一步非常简单，但实际上是我们发现让这一切运作的 秘密法则。

接收者只需计算：

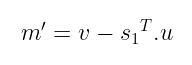
通过进行替换和消去，接收者得到的是：

现在……这很奇怪。通常，解密过程将恢复原始消息，但这 并不是 这里的情况。这是怎么回事？看起来我们遇上了麻烦。难道我们走入了死胡同？

拜托，伙计，我们知道我们没有。

当然没有！你看，m 和 m’ 之间的差异只是一些多项式。如果它们是 小的，那么 m 和 m' 的值将非常接近。而且，由于我们在发送信息之前适当地应用了 缩放，因此 m' 的系数将接近 0 或 10！

选好小多项式 s₁, s₂, e₁, 和 e₂ 是有帮助的！太好了！

因此，对于每个系数，我们只需选择离哪个更近——0 或 10。最后，我们通过除以 10 恢复原始消息！

可视化呈现：

这相当复杂，我知道。但从本质上讲，它与其他 加密方式 并没有多大区别：发送者有某种公钥，执行一些操作，并发送只有接收者的私钥可以解码的密文。

好的事情是，随着字段和多项式的大小越来越大，这个问题变得 难以想象地难 解，没有掌握秘密信息是不足以解决这一问题的。太棒了！

有关此方法的更多信息，我建议阅读 这篇文章 或 另一篇文章 。

Dilithium

除了加密，我们还应该将 数字签名 看作是密码学中的另一种基本操作。因此，显然，这是我们希望在 PQC 工具箱中拥有的下一类算法。

CRYSTALS Dilithium 是此类算法的首批之一。它是与 Kyber 所在的同一系列密码算法之一，称为 CRYSTALS。密钥生成与前面完全相同。

实际上没有多少其他要说的！让我们直接进入业务。

签名，第一部分

签名一条消息 M 需要几个步骤。我将把这一部分分为两部分以保持结构清晰。

我们以一种非常标准的方式开始：我们需要选择一个 随机数，就像其他签名算法一样。这一次，随机数是一个由短多项式组成的向量 _：

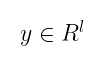
接下来的事情有点棘手。我们需要 承诺 到这个随机数，就像我们在椭圆曲线中通过 [k]G 操作做的那样。事情一开始相似：我们计算 w = A.y。然后，事情变得复杂：我们现在进行一个 压缩 步骤。

为了理解发生了什么，让我们关注 w 这个多项式向量的单一坐标——也就是说我们关注单一多项式 W(X)。它的系数是大有限域中的数字，因此它们可能是许多大型数字，这意味着它们会使我们的签名相当大。而通常我们并不希望那样。

这就是为什么压缩步骤是合理的。为了可视化，让我们想象我们有如下内容：

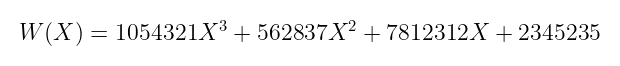
压缩步骤通过取某个数字 2ᵈ 并执行两个操作：

• 将 W(X) 的每个系数除以 2ᵈ，并向下取整。结果称为 高位。
• 然后，对 W(X) 的每个系数计算 mod 2ᵈ。这些称为 低位。

命名一开始可能显得奇怪。但当你意识到 2ᵈ 的二进制表示只是一个后面跟着 d 个零的 1 时，一切都变得有意义了！

这个计算确实很顺利，因为计算这两个操作时，除法实际上是将位平移 d 个位置，通过 mod 则可以得到数字的最后 d 位。

你不信？让我们一起举一个例子：

• 取数字 37610278412。它的二进制表示是 100011000001101111110100111000001100。
• 接下来，选择一个大约等于该数字一半位数的幂。在这种情况下，我们使用 17。所以，2¹⁷ = 131072。
• 我们计算高位为 ⌊37610278412 / 131072⌋，得到 286943。其二进制表示为 1000110000011011111。
• 最后，计算低位为 37610278412 mod 131072，结果为 85516；用二进制表示为 10100111000001100。

现在，像个时钟一样：

Boom!

好吧，这确实是个相当复杂的过程！让我们休息一下，欣赏这个过程的组织之美！

在 Dilithium 中，我们只保留多项式向量 w 每个系数的高位——我们将该结果记作 w₁。

如果你像我一样，在进行到这篇文章的这一阶段时，可能会有这样的感觉：

精疲力尽

好消息是我们离终点很近了！深吸几口气。这只需几分钟。

准备好了，就让我们继续。

签名，第二部分

我们有了压缩随机数承诺——但这只是签名的第一部分。设想一下，签名者将此承诺发送给验证者，作为回应，验证者发送一个 挑战 c，这只是一个系数为 -1、0 和 1 的小多项式。

有了这些，我们计算最终的签名值，公式为：

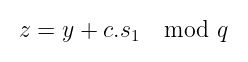
签名就是元组 (z, w₁, c)。

这里有一个重要的附加界限验证步骤，但为了简化，我们将略过。

现在，你可能已经注意到两件事：第一，签名中并未包含 消息 在任何地方；第二，按照我所描述的，这将是一个 交互式协议，而这是我们所不想要的。

我们已经知道，使用 Fiat-Shamir 变换，这可以通过一个 哈希 转变为 非交互式 签名方案。通过将消息引入混合，所有要求都得到满足！

因此，我们只需计算压缩随机数和原始消息的哈希（Dilithium 使用哈希算法 SHAKE，属于 SHA-3 家族）：

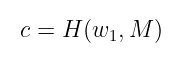
这只是一个二进制数字——我们需要将其转换为系数为 -1、0 和 1 的多项式。为此，我们使用的方法称为 拒绝采样。简单来说，可以看作：

• 00 映射为 0
• 10 映射为 1
• 01 映射为 -1
• 11 不被认为有效，因此我们丢弃该值，转向下一个两个比特。

实际上，这个映射稍微复杂一些，以确保大部分系数是 0。

哈希有点像从 随机分布 中抽样，我们以每次读取一对数据两位的方式生成 c 的每个系数。

不错！我们的签名完成了。验证是如何工作的？

验证

简单回顾一下：验证者持有公钥 (A, t)，现在还持有签名 (z, w₁, c) 和消息 M。

要验证，他们只需计算：

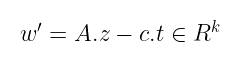
将正确的 z 值代入可以得到：

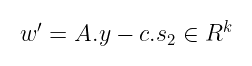
从本质上讲，w’与原始承诺 w 将会不同，但二者之间的差异只是小多项式 c.s₂——一些小的噪声。

换句话说，只有 w 和 w’ 中多项式系数的 低位 之间的差异会有所不同，而 高位 应该是相匹配的。看看这个！简直是魔法。

验证者只需要计算 w’ 的高位，并将结果与 w₁ 进行比较。如果匹配，则接受该签名！

同样，边界检查也很重要，可以防止伪造，充分利用 最短向量问题（SVP）在格子中的困难性，但我们会在这里略过。

有关详细信息，请参阅 原始论文。另外，对于 Dilithium 的另一种看法，请参阅 另一篇文章 以获取稍微不同的视角。

总结

这真是一场精彩的旅程，是吧？

这仅仅是后量子密码学蓬勃发展的新方法中的两个。并非所有被提议的方法都基于格结构，但外界有很多信息需要吸收，也可能有许多惊人的研究需要阅读（我还需要继续研究！）。

不过，基于格的密码学看起来是下一代标准密码算法的有希望的候选者。

此外，使用格的部分吸引力与它们的 特性 有关，这一点我们尚未讨论。因为一切都是基于 环 在幕后操作的，并且由于环支持两个操作，这为某些非常酷的东西提供了丰厚的土壤：全同态加密，或称为 FHE。这将是本系列的下一篇（也是最后一篇）文章的主题。

直到 下次再见！

• 原文链接： medium.com/thecapital/cr...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～