CRYSTALS Kyber：后量子加密的关键

CRYSTALS Kyber：后量子加密的关键

Kyber Logo — PQ Crystals

在数字领域，量子计算威胁着传统加密。NIST 的后量子密码标准化计划旨在制定新的加密标准。他们选择了一些先进的加密算法来抵御量子计算的力量。

量子计算：传统密码学的终结 \ \ 在当今的数字世界中，我们的秘密和数据之所以安全，要归功于那些需要超级计算机数百万年才能破解的强大代码。\ \ medium.com

Kyber 是这些被选中的算法之一，专为抵抗量子攻击而设计。其基于格结构的设计增强了数据安全性，应对潜在的量子威胁，为量子抗性加密提供了一条有前途的道路。

Kyber 是一种安全的密钥封装机制（KEM），其安全性依赖于在模块格上解决学习带误差（LWE）问题的难度。让我们深入探讨 Kyber 的核心力量，研究它如何驾驭 LWE 的复杂性，以确保在面对潜在量子威胁时的强大加密。

密钥封装机制 (KEM)

密钥封装机制（KEM）用于通过非对称算法在两方之间发送对称密钥。与 Diffie-Hellman 密钥交换方法 不同，KEM 使用非对称算法。在这种方法中，发送方使用接收方的公钥将对称密钥封装在密文中。收到密文后，接收方使用其私钥解封装并提取对称密钥，确保在传输过程中不直接共享对称密钥，从而实现了安全且经过身份验证的交换。

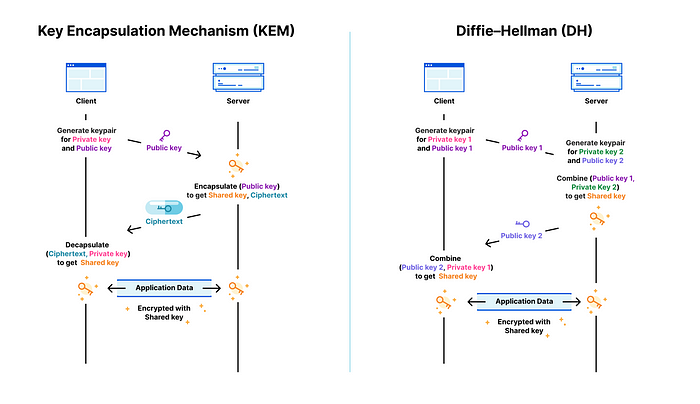
KEM vs Diffie-Hellman — Cloudfare

学习带误差 (LWE) 问题

想象以下线性方程组，其中 A 和 b 是公钥，s 是私钥向量，是方程 A × s = b 的解。通过使用高斯消元法可以轻松解决这个问题。在这种情况下，答案是 s = (0, 13, 9, 11)。

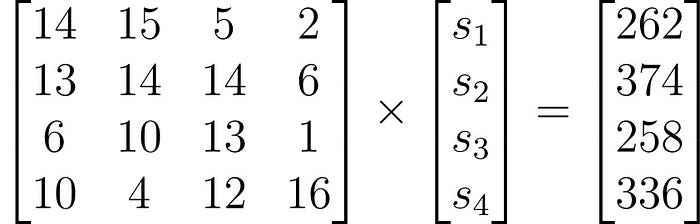
我们可以稍微修改这些方程，增加方程的数量，并引入一个小整数误差向量 e，使方程变为 A × s + e = b，这使得计算 s 变得更加复杂。此外，还添加了模运算以增加方程的复杂性。

环学习带误差 (Ring-LWE) 问题

这是基于格的密码学中的一个数学挑战，其目标是将一个秘密多项式隐藏在从结构化环中采样的噪声数据中。我将尝试提供一个简化的定义。

• a( x) 是多项式环 Z ₚ [X]/(Xⁿ+1) 中的一个多项式，其中所有系数来自 Zₚ
• e( x) 和 s( x) 也是 Z ₚ [X]/(Xⁿ+1) 中的多项式，具有小系数
• 那么，b( x) = a( x) . s( x) + e( x)，其中 b( x) 也是 Z ₚ [X]/(Xⁿ+1) 中的一个多项式

请注意，这里所有的 a, b, s 和 e 都是多项式，而在 LWE 中 A 是一个矩阵。现在让我们学习如何在多项式环中进行计算。

多项式环上的加法

这与传统多项式加法的方式类似，只是系数应来自 Zₚ。例如，如果环定义为模 x ³+1，则上述多项式加法的结果可能是 (2 x ²+3 x +1) + ( x ²−4 x +5) ≡ 3 x ²− x +6 (mod x ³+1)。

多项式环上的乘法

让我们使用以下示例来解释两个多项式之间的乘法如何工作。

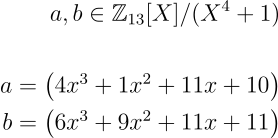
要进行乘法 a × b，我们将多项式 a 转换为一个循环矩阵。正如你在图像中看到的，矩阵 A 的每一列都是前一列的循环移位，最后一个元素在移位到前面时会取反。

Kyber 的工作原理

Kyber 规范参数

提供的表格显示了 Kyber 规范中 n、k 和 q 的值。然而，为了解释 Kyber 的工作原理，我们将使用更简单的参数：k=2，q=17，以及 n=4。

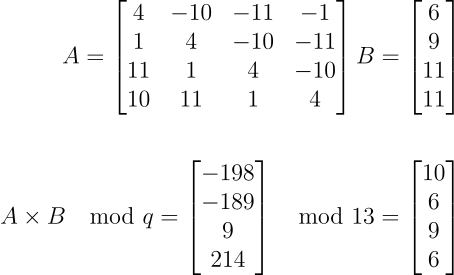
密钥生成

Kyber 的私钥使用 k 个具有 n 次数的多项式（称为 s）。这是使用随机小系数生成的。

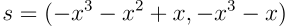
Kyber 公钥由两个元素组成。一个随机多项式矩阵 A（_k

• 原文链接： medium.com/@hwupathum/cr...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～