网络安全生日悖论！

你的网络安全生日！

我喜欢进行现场网络安全演示，当它们运行良好时感觉很棒。除了黑客攻击玩偶、水壶、体重秤和闭路电视摄像头外，我最喜欢的演示与密码学有关。这包括现场演示 RSA 和 Diffie-Hellman 方法，但我最喜欢的是执行哈希冲突的生日攻击。为此，如果我有一个 60 人的班级，我有 99.41% 的把握能成功找到两个生日相同的学生，即使班里只有 23 名学生，我也有大约 50/50 的机会找到两个生日相同的学生。为此，我需要匹配生日的同一天和月份（而不是年份）。

那么这是如何发生的呢？好吧，让我们想象一下我们有一个装有 1 到 365 编号的球的袋子，这些数字可以代表一年中的每一天。我将取出一个球并记下号码，然后将其放回袋子中。现在的挑战是，平均而言，在我抽到一个以前出现过的数字之前，需要尝试多少次。

那么让我们试试这个程序来估计我需要多少学生：

import random
days=365
array=[]
for i in range(1,days):
 x=random.randint(1,days)
 if (x in array):
  print(f"Duplicate found at {i}") # 在 {i} 处找到重复项
  break
 array.append(x)
 print(x, end =" ")

为此，我生成一个 1 到 365 之间的随机值（就像学生告诉我他们的生日时所做的那样）。然后我将其存储在一个列表中，然后检查该数字是否已被使用过。如果我运行几次，我会得到：

 % python 2.py
145 89 267 206 235 37 125 12 72 133 69 148 191 57 56 328 202 199
225 233 144 115 Duplicate found at 23 # 在 23 处找到重复项
% python 2.py
68 73 206 53 13 67 32 273 189 65 92 260 100 307 259 279 339 76 359
122 267 Duplicate found at 22 # 在 22 处找到重复项
% python 2.py
315 282 76 211 72 146 286 229 152 84 260 26 319 331 70 130 316 163
201 296 365 246 1 307 62 Duplicate found at 26 # 在 26 处找到重复项
% python 2.py
327 112 226 263 229 196 224 140 293 14 267 11 16 336 78 34 231 110 94
67 64 188 130 266 111 182 48 Duplicate found at 28 # 在 28 处找到重复项
% python 2.py
236 12 101 123 189 305 154 219 15 4 122 350 293 260 183 330 51 321 254
131 203 152 107 Duplicate found at 24 # 在 24 处找到重复项
% python 2.py
95 51 226 133 241 202 300 318 239 329 82 351 325 190 187 24 57 65 295 272
257 111 323 364 365 44 Duplicate found at 27 # 在 27 处找到重复项
240 291 314 258 352 262 142 9 12 123 162 182 98 15 146 361 29
Duplicate found at 18 # 在 18 处找到重复项
% python 2.py
121 211 290 312 55 60 176 97 158 276 159 308 154 325 266 148 206 321
133 5 282 Duplicate found at 22 # 在 22 处找到重复项
% python 2.py
45 331 308 327 363 292 5 287 Duplicate found at 9 # 在 9 处找到重复项

在这种情况下，这些值主要在 18 到 27 之间，但我很幸运地在仅尝试 9 次时就得到了一个重复项。我平均需要的实际尝试次数实际上是：

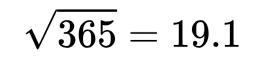
这种方法被称为平方根攻击。因此，让我们将其应用于二进制哈希，我们要在其中找到哈希冲突。为此，我们将拥有二进制值和一个给定的位长度，而不是一年中的天数。现在，我们可以将这些值表示为我们拥有的数字的 2 的幂。因此，我们可以有 256 (2⁸) 个不同的值，而不是 365，它们表示从 0000 0000 到 1111 1111 的值。那么，让我们试试这个：

% python 2.py
133 49 183 170 181 23 173 19 29 Duplicate found at 10 # 在 10 处找到重复项
% python 2.py
26 256 183 139 224 229 111 1 209 121 245 180 57 101 179
88 Duplicate found at 17 # 在 17 处找到重复项
% python 2.py
209 78 108 5 195 142 14 100 187 151 126 109 129 238 42 244 56 176 45
162 75 159 23 174 97 215 251 132 35 236 204 175 182 1 160 Duplicate found at 36 # 在 36 处找到重复项
% python 2.py
27 96 98 162 229 159 15 21 5 131 2 51 88 93 123 173 191 Duplicate found at 18 # 在 18 处找到重复项
% python 2.py
43 188 62 163 110 4 59 52 69 51 18 85 252 111 170 145 35 118 66 15
189 181 2 174 71 214 120 104 24 180 97 12 68 235 Duplicate found at 35 # 在 35 处找到重复项
% python 2.py
199 129 136 189 186 195 30 192 191 71 52 26 53 Duplicate found at 14 # 在 14 处找到重复项
% python 2.py
66 26 147 21 168 247 130 52 78 28 146 64 240 180 37 4 59 166 142 173
156 60 223 2 234 256 82 181 153 194 123 35 138 Duplicate found at 34 # 在 34 处找到重复项
% python 2.py
30 36 207 176 113 102 40 186 228 140 81 51 43 173 42 221 56 27 196 9 33
115 78 249 Duplicate found at 25 # 在 25 处找到重复项
% python 2.py
46 212 78 214 201 4 26 121 37 195 8 55 102 130 197 199 236 24 162 91
Duplicate found at 21 # 在 21 处找到重复项

同样，我们将进行平方根攻击，现在我们可以将其概括为：

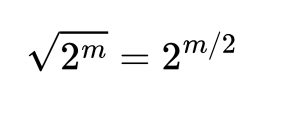
因此，对于一个 8 位的值，平均而言，我们将在 2⁷ (128) 次尝试中找到冲突。对于哈希，我们可以使用 MD5 哈希，它有 128 位。因此，将有 2¹²⁸ 个不同的哈希值，我们将在 2⁶⁴ (18,446,744,073,709,551,616) 中找到冲突。因此，如果我们使用一个快速破解器，每次尝试哈希需要 1 纳秒，那么找到冲突的平均时间将是 18,446,744,073 秒（213,503 天）。但是假设我们使用具有 4,000 个内核的 GPU，现在将需要 533 天。现在，让我们使用一个 32 个 GPU 的阵列。这只需要 16 天多一点：

>>> 2**64*1e-9/60/60/24/400/32
16.67999861989073

现在，我们可以使用图像来实现生日攻击，我们可以获取两个图像（x_1 和 x_2），然后修改每个图像以获得 x_1' 和 x_2'。如果我们对这些图像进行 MD5 哈希，平均而言，在 2⁶⁴ 次尝试后，我们应该能够得到：

h(x_1') = h(x_2')

后来，Nat McHugh 做了这个实验，拍摄了 James Brown 和 Barry White 的照片，并设法在 AWS GPU Cloud 上仅用了 10 个小时就获得了冲突：

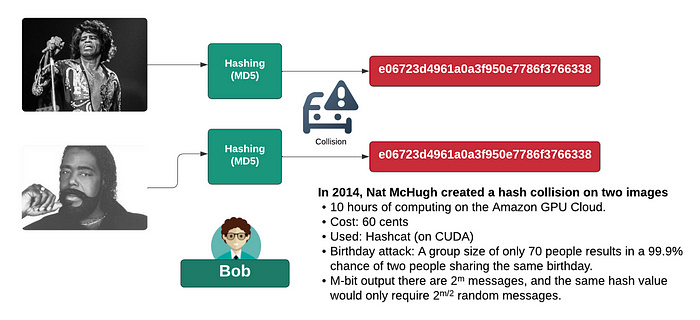
有了这个，他随机地将比特塞入图像中，这些比特是看不见的，并设法使用生日攻击创建了一个冲突。

更大的哈希值呢？

好吧，你可以看到 MD5 很容易受到攻击，但是像 SHA-1 这样更大的哈希呢？好吧，这要困难得多，因为我们现在有一个 160 位的哈希，因此将在 2⁸⁰ 中发生冲突。从我们之前的设置中找到冲突的平均时间是：

>>> 2**80*1e-9/60/60/24/400/32
1093140.3895531588

这是 1,093,140，超过 100 万天，而不是 MD5 的 16 天。但是，谷歌设法投入了大量的计算能力 [ 在这里]：

为此，他们设法在 SHA-1 的两个 PDF 文档的哈希上产生了冲突。这需要大量的计算能力，并且花费了超过 18 个月的时间才能完成，但他们至少表明这是可以做到的。这就是 SHA-1 在互联网中被弃用的原因。至于 SHA-256，甚至不要尝试找到冲突，因为它会花费你超过：

300,000,000,000,000,000,000 天

仅找到一个，并消耗足够的能量多次煮沸地球上所有的海洋。

量子破解

最后，Grover 表明生日攻击适用于量子破解，我们必须搜索的哈希或密钥的数量是：

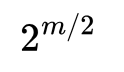
这意味着 AES 的 128 位加密密钥现在容易受到生日攻击的影响，以及 160 位哈希值。因此，我们需要转向 256 位 AES 和 256 位哈希方法（SHA-256 或 SHA-3），以确保量子计算机不会破解我们的加密和哈希方法。

跋

如果你想了解生日攻击对于给定规模的受众的成功概率，请尝试这里：

生日攻击 \ 生日攻击方程确定了给定 n 个人时，两个人拥有相同生日的概率。相同...... \ asecuritysite.com

总的来说，你会发现 23 是一个房间里两个人有相同生日的概率达到 50/50 的数字。

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～