Solidity 中 Merkle 树的第二原像攻击
- RareSkills
- 发布于 2023-11-26 14:48
- 阅读 1573
文章详细介绍了Merkle树中的第二原像攻击(second preimage attack),解释了攻击的原理及如何防御这种攻击。文中使用了具体的示例和代码片段来阐述攻击的实现,并提供了OpenZeppelin库中的防御方法。
Merkle树中的第二原像(second preimage)攻击发生在当Merkle树中的一个中间节点被展示为叶子时。
这个攻击的名称相当误导,因为它暗示哈希有第二原像。现代哈希函数没有多个(可计算的)原像。
这个攻击的更好名字应该是“节点作为叶子攻击”或“缩短证明攻击”。
前提条件
我们假设读者熟悉Merkle树和Merkle证明。
符号
我们将h(x)称为x的哈希值。h(x + y)是x和y的连接的哈希值。本文中,我们将重点关注keccak256作为我们的哈希函数;选择一个特定的函数将有助于进一步阐明某些推理。然而,请记住,本文中的思想适用于任何哈希函数。我们用ℓ表示Merkle树的叶子。第_ith_个叶子用ℓᵢ表示。
一个示例攻击
假设我们希望为下图中的叶子2 (ℓ₂) 创建一个证明。叶子将是ℓ₂,证明将是\[h(ℓ₁), h(b), h(f)\]。a、b、c、…、g的值是子值的连接。我们接受证明,如果h(g)等于Merkle根。
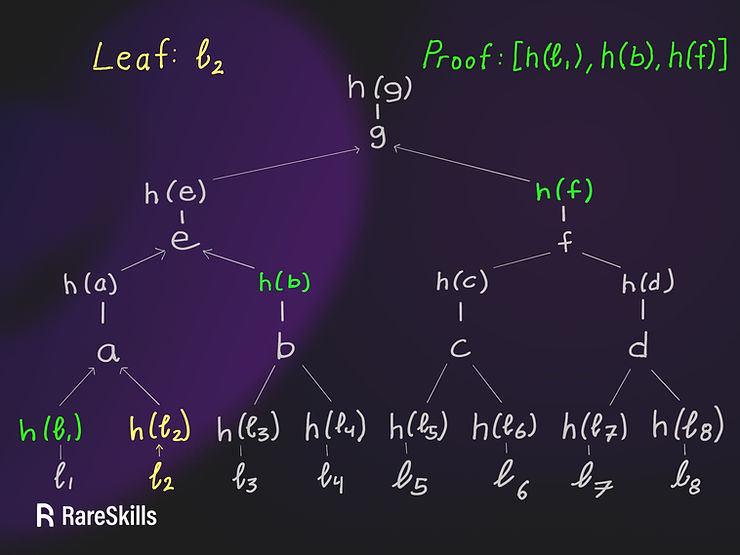
证明将是\[h(ℓ₁), h(b), h(f)\],标记为绿色。到根的证明是
h(a) = h(h(ℓ₁) + h(ℓ₂))
h(e) = h(h(a) + h(b))
h(g) = h(h(e) + h(f))
return root == h(g)
第二原像攻击
如果攻击者提供了a作为叶子,并给出\[h(b), h(f)\]作为证明,会怎样?
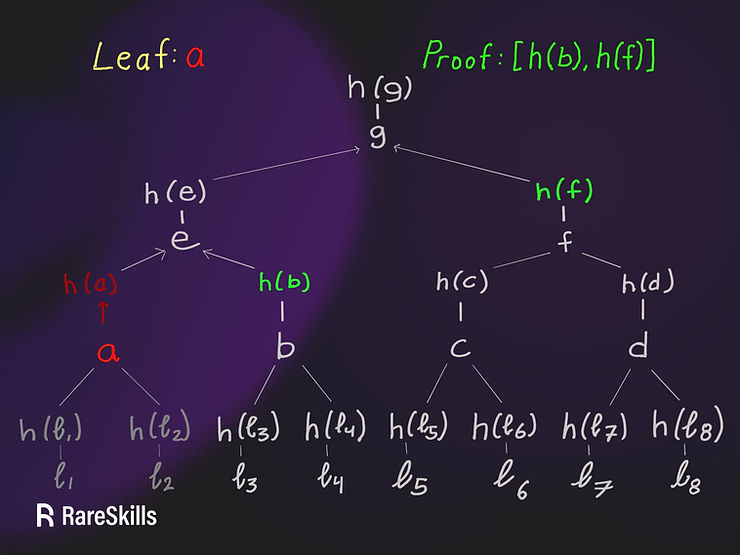
合约将a视为一个叶子,其中a = h(ℓ₁), h(ℓ₂))。如果证明是[h(b), h(f)],Merkle证明将被接受为有效。
实质上,如果一个Merkle证明有效,那么如果我们将原始证明中的第一个值传递作为叶子,它的缩短版本也是有效的。
因此,攻击者将提供一个“叶子”和一个合约接受的证明,但所提供的“叶子”在原始Merkle树中并不是一个叶子!
那么我们如何防止这种情况发生?
OpenZeppelin警告
在OpenZeppelin Merkle树库中,我们在注释中看到警告以及一些解决方案。我们将在以下部分解释它们的解决方案。
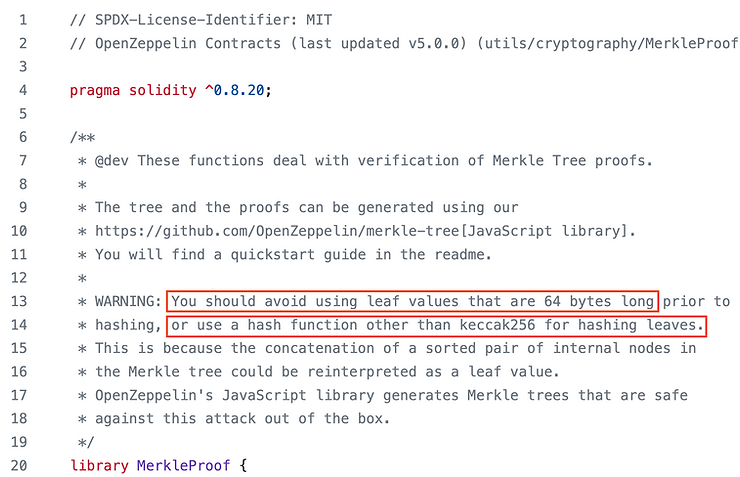
以下两个部分将解释这两种解决方案是如何防止该问题的。
攻击需要64字节叶子
为了使这次攻击有效,攻击者必须传递中间节点的原像,而不是其哈希值。这意味着必须将a作为叶子,而不是hash(a)。由于Solidity使用32字节哈希,a = h(ℓ₁) + h(ℓ₂)将是64字节长。
如果合约不接受64字节的叶子作为输入,那么攻击将无法进行。
也就是说,如果叶子的输入长度不是64字节,则不可能将h(ℓ₁) + h(ℓ₂)作为错误的叶子值传递。
使用不同的哈希作为叶子的防御
如果我们的应用程序出于某种原因需要接受64字节的叶子,那么我们可以通过对叶子使用与证明不同的哈希来防止攻击。
也就是说,当叶子首次被哈希时,我们使用与对根哈希所使用的不同的哈希。这将防止攻击者将中间值“重构”为一个叶子。参考上面的图示,攻击者使用h(a)来创建假“叶子”。然而,如果叶子通过h’(a)进行处理,则中间值无法被重构。
OpenZeppelin使用双重哈希作为“不同的哈希”
OpenZeppelin干脆利用双重哈希,而不是使用不同的哈希函数(例如通过预编译,这将花费更多的gas)。也就是说,h’(x) = h(h(x))。
我们用绿色下划线显示了哪里进行了双重哈希,以从底层数据构建叶子节点。
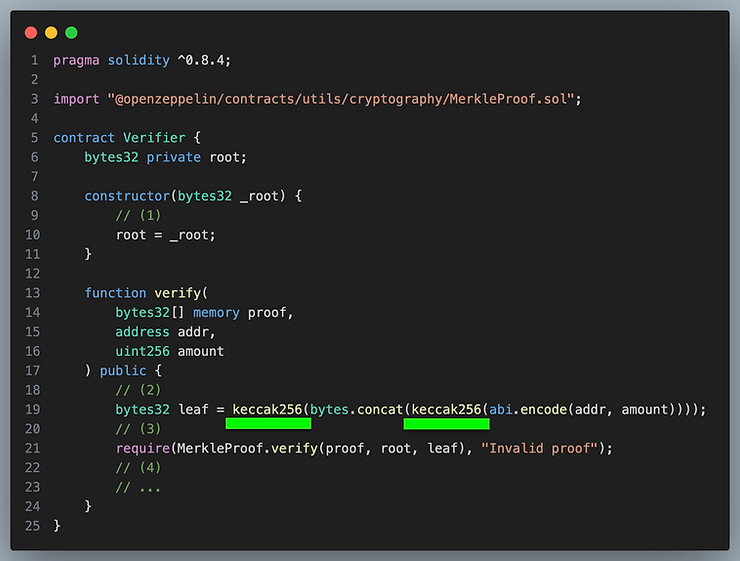
请注意,该库并不强制你对哈希进行两次——实际上,根本不强制你对叶子进行哈希处理!不对叶子进行哈希处理可能开辟了除了第二原像攻击之外的攻击路径——请参阅最后的练习问题。
结论
第二原像攻击能够有效,因为我们可以提供一个有效证明的缩短版本并重建Merkle根。Merkle根确实有一个原像——然而,根是在增量中创建的——而不是通过一次哈希整个证明来完成的。通过从序列中的后期开始证明,我们可以得到一个替代输入,生成相同的根。
防御此攻击很简单——只需不允许非叶值被解释为叶子。
练习问题
以下的旗帜捕获练习不当使用Merkle证明,因此可以被攻击。
RareSkills Riddles: Furry Fox Friends
更多
请查看 区块链训练营 进行系统学习
最初发表于2023年11月24日
- 原文链接: rareskills.io/post/merkl...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 170 浏览
- 黑吃黑:重入攻击秒提ETH+瞬锁修复 449 浏览
- TupleHash:一项NIST标准 503 浏览
- 基于哈希函数的签名(三):多次签名 723 浏览
- 基于哈希函数的签名(二):少量次数签名 891 浏览
- 基于哈希函数的签名(一):一次性签名 848 浏览

