削减或大多数奖励的问题
- a16z Crypto
- 发布于 2023-01-21 19:14
- 阅读 1564
本文探讨了如何激励区块链投票中的知情参与,并分析了现有机制的局限性。尽管通过奖励投票给少数投票者的方案似乎有前景,但实际上由于道德风险(如无法观察到投票者是否知情)而导致实施成本高昂。此外,文章提出了一些实际建议,以解决激励恶意行为和机器人投票的问题,包括设定先前贡献的要求和结合质押或锁定要求。
在我们上一篇文章中,我们展示了如何设计一个机制,旨在让人们诚实地报告他们认为投票的成本,并对那些认为投票成本最低的投票者进行补偿。但正如许多人指出的,激励原始参与可能会导致不知情的投票或机器人投票。
各种项目和作家建议奖励在多数中投票的投票者和/或对在少数中投票的投票者落实惩罚,以创造对知情投票的激励。我们认为,对这个问题进行正式分析是有必要的。在这里,我们确定尽管通过这种方式激励知情参与是可能的,但即使在优化的、最具成本效益的形式下,这样做可能会成本过高。此外,奖励结构相对而言更难以解释,这也可能成为实施中的障碍。
这两个挑战的原因是一个潜在的道德风险问题——人们是否真正知情是不可观察的,因此你需要确保你不仅仅是在激励他们去猜测多数将如何投票。因此,基于他们是在多数还是少数中投票来奖励或惩罚选民,通常可能不是有效的做法。这一发现可能有助于理解在其他背景下对扭曲结果的大规模洗牌导致的选票效应(或等效地,奖励公投中的投票地址)的微妙影响,这将是未来工作的主题。
在展示了直接为“知情”投票付费的缺点之后,我们总结了一些具体想法,以帮助项目尝试防止机器人或恶意参与者的不良投票奖励。特别是,项目可以考虑:
- …将奖励仅限于以前对项目有贡献的地址,这类似于其他类型的追溯性奖励中的持续实验,以及
- …将奖励项目与某种类型的质押要求和/或锁仓要求结合使用,使得短期内收割奖励变得不划算。
为什么为“知情”投票付费很困难
如果项目唯一想做的只是激励投票,那么直接揭示或递增奖励的 VCG 机制实现就能够完成这个任务。但单靠投票可能不足以实现平台的目标。它可能想要激励某些子集的投票者以一种知情的方式投票。
激励知情投票比仅仅激励投票要困难得多。几乎可以肯定,无法确定投票者实际上是否以知情的方式投票——信息投资在很大程度上是不可观察的。有些人提出,投票于多数可能是以知情的方式投票的一个迹象。直觉是,项目成员常常对其目标有相当大的共识。因此,我们可能认为,如果每个人都做足了功课,每个人大致会得出同样的结论,关于怎样达到这些目标。
那么,第一个问题是,我们是否可以通过激励多数投票来激励知情投票。
与多数一起投票
一开始,区块链投票的运作方式就带来了挑战。目前,对于大多数区块链投票系统,投票结果实时可见。也就是说,如果投票者 2 在投票者 1 之后投票,投票者 2 就知道投票者 1 如何投票。一旦我们引入激励以支持多数投票,这种情况显然会产生“群体效应”问题——后来的投票者即使对正确的投票选择有不同的意见,他们也会根据多数的投票结果进行投票。
但是,即使我们假设我们有一个在所有人投票后模糊投票结果的区块链投票技术,我们仍会面临相当大的挑战。基于与多数投票进行知情投票的激励:
- …这不便宜,部分原因在于我们无法直接观察到谁变得知情,这需要过高的补偿来给出强烈的激励,避免仅仅通过猜测政策将是多数选择来“假装”变得知情。
- …这难以理解,因为它要求潜在的投票者能够报告他们参与的成本和获取信息的成本,并根据这些成本评估合同。
- …无法保证成功,因为总是可能出现协调失效的情况,如果投票者相信其他投票者的投票不是知情的,他们自己就没有激励去知情。
考虑到这些缺点,我们认为,在大多数情况下,项目不太可能依靠奖励投票者以获得多数投票作为一种激励知情参与的方法,即使拥有最佳设计的激励机制。
实施知情投票的最佳机制
假设平台希望 n 名投票者投票,并希望 m ≤ n 名投票者以知情方式投票。每个代币持有者有两个不同的成本:他们投票的成本 (c_i) 和收集信息的成本 (k_i)。
为了简单起见,我们做出四个假设。
- 投票在两个选项之间进行,A 和 B,在投资任何信息之前,每个人都认为 A 是正确选择的概率是 q > ½。
- 如果代币持有者投资于信息,他们会准确地了解正确选择。(将分析扩展到更现实的概率情况是相对简单的。这样做只会使知情投票的实施更昂贵。)
- 代币持有者并不直接关心结果,只关心他们的补偿和成本。
- 高投票成本和高获取信息的成本是完全正相关的——也就是说,我们可以将投票者排列成 1 到 N,使得 c_1 < c_2 < ... < c_N 和 k_1 < k_2 < ... < k_N。(放宽这个假设会增加成本和复杂性。)
平台将代币持有者分为三个组:
- 组 V:n– m 名代币持有者提供 p_V 的补偿以便简单投票。
- 组 I:m 名代币持有者提供 p_I 的补偿,只有在他们与组 I 的其他成员投票一致的情况下才能获得。
- 组 O:剩余未提供任何补偿或激励的代币持有者。
该机制必须将代币持有者分组,并选择补偿,以尽可能有效地实现两个目标。首先,它必须使代币持有者诚实地透露他们的成本。其次,它必须激励代币持有者按照预期行为表现(即 V 组的成员投票,而 I 组的成员进行知情投票)。
首先考虑如果变得知情是可观察的最优机制,这样 p_I 就是实际得知知情与否,而不是在于与多数投票的条件。(这将是我们在第一篇文章中讨论的 VCG 问题的一种稍微更复杂的版本。)为了尽可能降低成本,机制将最低成本的代币持有者(1 到 m)放在组 I 中,将下一个最低成本的代币持有者(m + 1 到 n)放在组 V 中,如图 1 所示。同时,就像我们早期文章中提到的,为了使代币持有者愿意诚实地揭示他们的成本,该机制会为每个代币持有者提供等于其外部性补偿——即,他们存在对除自己以外的每个人的总福利的影响。现在看看这些支付是多少。
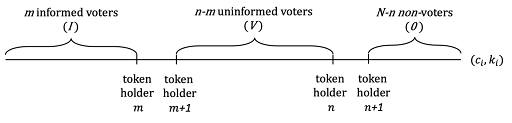
图 1. 将代币持有者分为三组:最低成本的代币持有者成为知情投票者(I),下一个最低成本的成为无知投票者(V),其余成为无投票者(O)。
投票者在组 V 的外部性是什么?如果该代币持有者被移除了,为了使投票者数量回到 n,投票者 n + 1 将不得不以成本 c n +1 投票;这是任何组 V 中的投票者对总福利的影响。因此,提供给 V 组成员的补偿将是 p_V = c n +1 。如图 2 所示。

_图 2. 如果无知的投票者被消除,为了保持 n,代币持有者 n + 1 必须被转移到无知投票组,承担投票费用 c_n + 1。_
组 I 中的代币持有者外部性是什么?如果该代币持有者被移除,那么为了将知情投票的数量恢复到 m,第 m + 1 个投票者将必须被移入组 I,并进行知情投票。此投票者已经承担了投票成本,但现在还必须承担获得信息的成本,费用为 k m +1。此外,我们还需要将新成员添加到组 V 中,以使投票者数量恢复到 n。这将是投票者 n + 1,他们必须以成本 c n+ 1 投票。因此,组 I 中的代币持有者对其他代币持有者的总福利的影响是 c n +1 + k m +1 ,这就是他们各自提供的补偿, p_I = c n +1 + k m +1 。如图 3 所示。

_图 3. 如果知情投票者被移除,为了保持 m 名知情投票者,代币持有者 m + 1 必须被移入知情投票组,承担额外的信息成本为 k m +1。同时,代币持有者 n + 1 必须被转移到无知投票组,以保持总投票者数为 n,承担投票费用 c_n + 1。_
如果机制可以直接条件化代币持有者的行为——也就是说,如果变成知情的过程是可观察的——这将是完整的答案。正如我们在附录中所展示的,这些补偿会引导代币持有者诚实表达。而且没有其他更便宜的方法来做到这一点。
道德风险问题
上述分析是不可执行的,因为我们实际上无法观察组 I 中的某个代币持有者是否以知情的方式进行了投票,因此我们无法根据是否知情来条件化补偿。这就是人们对以组 I 的多数人投票以条件化补偿 p_I 的兴趣——基于我们假设知情的投票者会准确知晓真相,如果 I 组中的其他人均进行知情投票,I组的成员可以通过知情保障自己获取支付。因此,为多数投票者付费激励他们投资信息。
但是,这种激励没有上面所创建的激励那么强,因为道德风险问题通过不可观察性而产生。如果投票者依据与多数人投票来获得奖励,他们可以变得知情,并且(假设其他人也知情)确保获取支付。但他们也可以选择不进行知情,估计多数将如何投票。如果他们猜对了,他们仍然会获得支付,而不用承担获取信息的成本。
这种选项削弱了 I 组成员在信息投资方面的激励。此外,还会出现另一种复杂情况。如果组 I 的补偿过于慷慨,以至于相对于组 V 的补偿,代币持有者应被放入 V 组可能会有 incentive 低估他们的成本,使自己被分配到 I 组,并进行无知投票,希望能够猜对。因此,要完整表征最佳机制,我们必须将这些道德风险考虑在内。
要分析这个问题,我们必须询问代币持有者能够多少概率正确投票,尽管没有变得知情。假设 I 中的所有其他成员都变得知情。那么,关于 A 的投票为 q,而关于 B 的投票为 1-q。也就是说,无知的代币持有者的最佳猜测是 A,而猜对的概率为 q 。因此,组 I 的投票者 i 做出最佳猜测,预期收益为 q · p_I − c_i。
这里需要强调的是,我们以重要的方式改变了对可实施性的提问。VCG询问所期望的行为能否作为一种弱主导策略实施——也就是说,代币持有者希望按预期行为行动,无论其他人做什么。由于获得对多数投票的补偿的条件,弱主导可实施性不再可能,因为获取支付与其他所有投票者的投票结果相关。因此,我们现在是在询问所希望的结果是否为弱可实施的。如果存在这样一个存在于代理人行为与我们期待相符的纳什均衡怎么办?正如我们将在下面讨论的,即便当答案是肯定时,也可能存在其他纳什均衡。
首先,考虑一名应归入 V 的代币持有者。如果该代币持有者如实陈述,则会被置于 V 中,获得的收益为 p_V - c_i。如果他们谎报以进入 I 组并做出最佳猜测,则会获利 q · p_I − c_i。比较之下,这名代币持有者如果:
- p_V ≥ q · p_I 便会如实反映他们的成本。
其次,考虑应该归入组 I 的代币持有者。如果该代币持有者变得知情,则收益为 p_I − c_i − k_i。如果他们不获取信息并做出最佳推测,则收益为 q · p_I − c_i。比较之下,这名代币持有者会变得知情,如果满足:
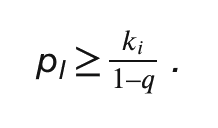
最优机制
上述分析为引导真相和正确行为必须满足的四个约束条件提供了清晰的标识。它们是:
-
p_V ≥ c_n + 1
-
p_V ≥ q · p_I
-
p_I ≥ c_n + 1 + k_m + 1

最后一个约束对于组 I 中最高成本代币持有者 m 来说是最难以实现的。当然, m 的支付不能直接依赖于他们的成本,因为这样他们会有激励夸大该成本。因此,最便宜的方法来解决最终的约束,同时引导真相,是:
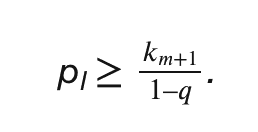
这现在为我们提供了最佳机制的完整表征。我们有:
-
组 I
- 包含代币持有者 1 到 m。
- 每个成员获得 **p_I* 的支付,取决于与 I** 组的多数人投票。该支付为:
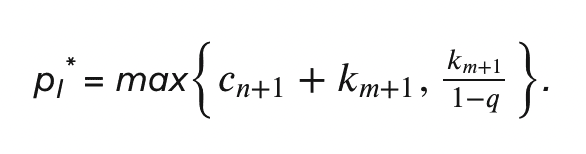
-
组 V
- 包含代币持有者 m + 1 到 n。
- 每个成员获得 **p_V*** 的支付以投票。该支付为:
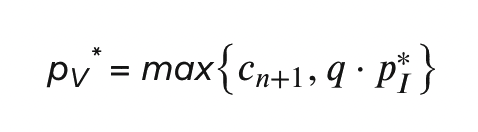
请注意 p_I 和 p_V 各自取两个值。它们所取的值依赖于 q 和 c_n + 1 及 k_m + 1 的相对值,正如我们在附录中明确说明的那样。但正如图 4 所示,这些作为 q 的函数的支付的基本形状始终是相同的。
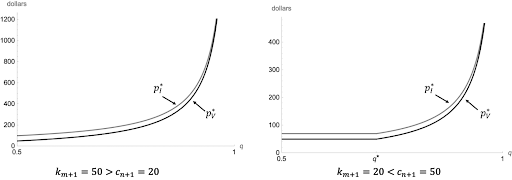
_图 4. 根据总支付应对两个组最优支付函数与 q 的关系,值为 c_n + 1 和 k_m + 1 的两个不同选择。_
示例
为了说明这种机制,考虑一个例子。假设有五名代币持有者,每个持有一枚代币,成本如下。
| 代币持有者 | 投票成本(c_i) | 信息成本(k_i) |
| 1 | $2 | $3 |
| 2 | $4 | $5 |
| 3 | $9 | $11 |
| 4 | $12 | $14 |
| 5 | $14 | $15 |
项目希望 n = 3 人投票,并希望至少 m = 2 名以知情方式投票。此外,假设项目认为 A 是正确选项的概率为 q = 0.6。
该项目要求每位代币持有者披露其成本,代币持有者也这样做。平台找到以下两个数字: c_n + 1 = 4 = $12 和 k_m + 1 = 3 = $11。
我们的机制选择:
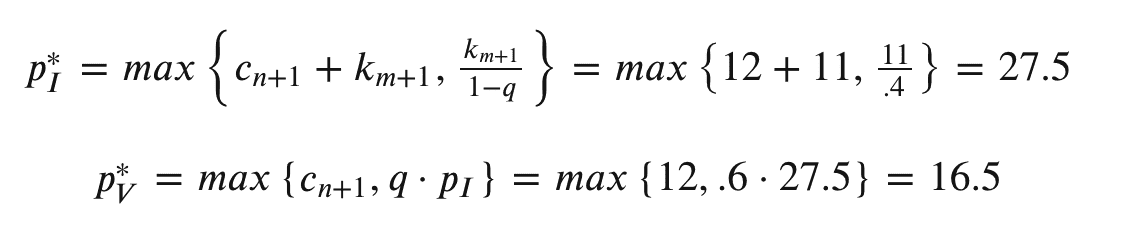
代币持有者 1 和 2 被分配到组 I,进行知情投票,每人获得 $27.5 的补偿。代币持有者 3 被分配到组 V,进行无知投票,获得 $16.5 的补偿。
激励知情投票的顾虑
我们已经表征了通过激励人们以多数票投票获得知情投票的最优机制。该机制的三个特征突显了在实际实施此类激励机制中存在的真实顾虑。
首先,提供正确的激励可能非常昂贵。在我们的例子中,代币持有者承担的投票和信息的总成本为 $23 (代币持有者 1 和 2 承担投票和信息的成本,代币持有者 3 仅承担投票成本)。然而,该机制支付的补偿总额为 $71.5 (代币持有者 1 和 2 各获得 $27.5,而代币持有者 3 则获得 $16.5)。不幸的是,由于平台不知道投票者的成本,没有更便宜的方法来实现该目标。
更一般而言,产生 m 个知情投票和总共 n 个投票的总成本是
总成本 = m · p_I\ + (n – m) · p_V。
此总成本依赖于三个因素:
- 需要购买的投票和知情投票的数量(m 和 n – m),
- 代币持有者的投票和信息成本(c_n + 1 和 k_m + 1),及
- 对正确选择的不确定性有多少(q)。
平台的成本在 m、n – m、c_n + 1 和 k_m + 1 中线性递增。但如图 4 所示,随着 q 增加,它们的增长是超线性的。此外,随着 q 接近 1,因为几乎确定 A 是正确的选择,诱导知情投票的成本趋于无穷大。这是因为如果 A 几乎肯定是正确选项,I 组的代币持有者没有理由投资于获取信息。他们可以只投票 A,几乎肯定会在人群中获得多数。因此,考虑购买知情投票时,只有在对正确选择有相当大的不确定性时才是可行的,也就是说,当 q 接近于 0.5 时。幸运的是,这也可以看出,在这种情况下知情投票的价值最大。
第二个担忧是该机制可能对代币持有者来说有些难以理解——尽管代币持有者的要求可能没有数学上所暗示的那么繁重。代币持有者需要能够(1)陈述其投票和获取信息的各自成本,以及(2)在获得简单的合同时理解其经济激励的方向。
第三个担忧则更为根本。任何基于选民在其所在小组中投票多数的激励机制都存在协调问题的顾虑。即,以上分析表明其均衡能使所有代币持有者按照所描述的方式表现,但始终存在其他均衡。
想象一下,某个投票者在 I 组中认为没有其他代币持有者会投资于信息。那么,这代币持有者就认为,知道正确选项并不能帮助他们在小组 I 中投票多数,因为人数的投票结果不会由正确选项决定。因此,该代币持有者就没有投资于信息的激励。因此,在激励机制中,因此,除了“知情”均衡外,始终还有一个“无知”均衡,使得所有代币持有者都不投资于信息,因为他们(正确地)认为其他代币持有者不会投资于信息。
\\*\
我们的分析得出的结论是,基于投票者是否在多数或少数中进行投票来奖励或惩罚他们,并不是在激励投票的同时抑制不知情投票或机器人投票的最佳方式。
对于认为基本奖励机制过于脆弱易被操控或不知情投票的项目,一个合逻辑的起点是仅向有过贡献记录的地址提供奖励。这将符合最近在追溯奖励方面的实验,如 Optimism 的持续工作。
单独或附加地,项目还可以探索质押要求,仅在地址被锁定在该协议内较长时间时才提供奖励,以此抑制短期内的投票奖励收割。
\\*\
Ethan Bueno de Mesquita 是芝加哥大学哈里斯公共政策学院的悉尼·斯坦教授。他的研究聚焦于博弈论模型在各种政治现象中的应用。他为技术公司和其他组织提供治理及相关问题的建议。
Andrew Hall 是斯坦福大学商学院的政治经济学教授,也是政治学教授。他与 a16z 研究实验室合作,并为技术公司、初创公司和区块链协议在技术、治理和社会交集问题上提供咨询。
\\*\
编辑:Tim Sullivan
\\*\
附录
VCG 在获取知情时的真实性
如果变得知情是可观察的,那么 p_V = c_n + 1 和 p_I = c_n + 1 + k_m + 1 则能够引导代币持有者如实表达。
首先,请注意,所有参与该机制的人都将感到满意。每个最终会归入组 V 的代币持有者获得的收益为 p_V - c_i。因为 p_V = c_n + 1,而组 V 的成员的成本均为 c_i < c_n + 1,因此他们获得正收益。类似地,组 I 的每个代币持有者的收益为 p_I - c_i - k_i。由于 p_I = c_n + 1 + k_m + 1,而组 I 的成员成本均为 c_i < c_n + 1 和 k_i < k_m + 1,他们也获得正收益。
其次,对于所有代币持有者来说,说真话是一个弱主导策略。
如果 V 组的成员声称有更高的成本,可能略无变化或达到了零收入;如果组 V 的成员是否声称有更低的成本,可能或者并未发生变化,或者晋升至 I 组。在这种情况下,他们可得收益是 p_V + k_m + 1 - c_i - k_i,但由于 V 组成员的信息成本 k_i >= k_m + 1,tailang这不足以超越他们的补偿利润。
如果组 I 的人声称有更低的成本,他们依旧留在组 I,因此まして给出同样的收益。如果声称更高的成本,结果是收益无变化(如果留在组 V),或被分配至 O 组并获得零收入(显然不划算),或被归入组 V。在那种情况下,他们的收益将是 p_V = c_n + 1 - c_i。但由于组 I 的成员信息成本 k_i < k_m + 1,这明显不如他们在组 I 中的收益。
作为成本的支付函数 c_n + 1 < k_m + 1 和 q
在文本中我们已展示
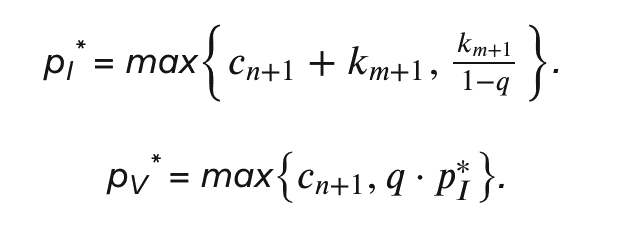
从中很容易推导出:
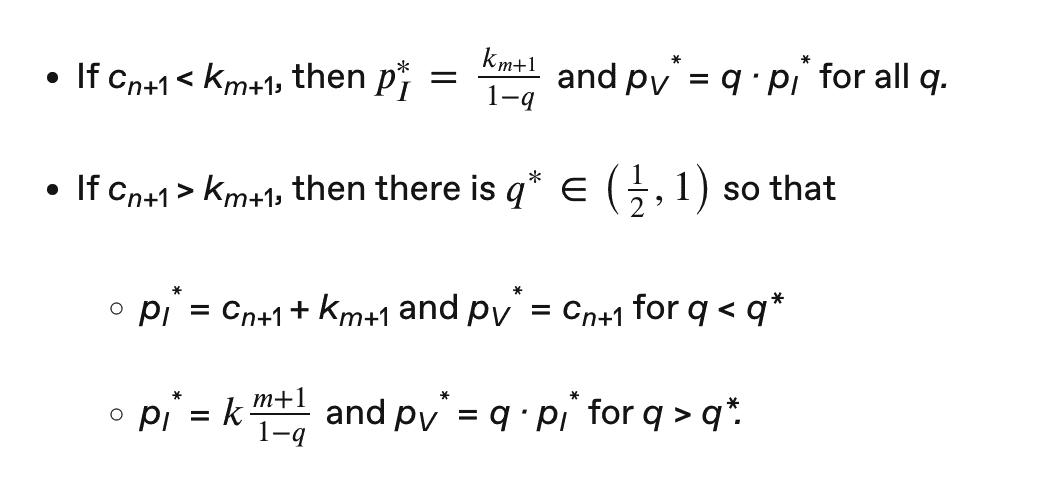
\\*\
- 原文链接: a16zcrypto.com/posts/art...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 如何修复代币 49 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 338 浏览
- 影响市场:解决预测市场衍产品的“如何”和“为什么” 374 浏览
- 第一 DeFi 协议 - Aave 911 浏览
- $META 看涨情景分析 708 浏览
- 机构团队如何构建持久的流动性质押协议 445 浏览
- 廉价生成与理解的脆弱性 476 浏览
- 29. 加密货币及其经济模型:世界级的理论,实习级别的执行,崩盘的价格 644 浏览
- 14. “去中心化乌托邦”?真可爱Maxis Breathe 仍然由少数钱包控制 998 浏览
- 第九季:从实验到组织 - Optimism 666 浏览
- Arcade 代币:最被低估的代币类型 581 浏览
- Web3协议中作为攻击向量的治理 2711 浏览

