激励匿名参与 - 经济学

关于激励匿名参与

\cdot⋅

\ upload_0bca3fb7f6b0d2fc3fe0596f285311121300×867 189 KB

\cdot⋅

要点总结： 区块链活动是由参与共享协议的独立参与者促成的。激励这种参与是一项关键的设计考虑因素，尤其是在无需许可的、对抗性的和假名环境中。我们在第 1 节中提出了一个模型，并对参与博弈进行了论证。在第 2 节中，我们分析了该博弈的对称、匿名均衡。然后，我们在两种设置中应用此框架。第 3 节详细介绍了证明者市场，该市场旨在激励至少一个证明的生成。第 4 节转向工作量证明协议，该协议旨在激励至少 50% 的参与（其动机是避免 51% 攻击的目标）。在这两种情况下，我们都推导出了协议的最佳激励结构，以最大限度地降低其成本。我们将在第 5 节中进行总结，讨论如何扩展该模型以及用于引导参与的其他特定于区块链的技术。

\cdot⋅

作者：maryam & mike – 2025 年 5 月 26 日。

\cdot⋅

感谢 Akilesh, Noam, Matt, 和 Barnabé 对本文的审阅和讨论!

---

目录

(1). 动机与模型

(1.1). 参与博弈模型

(1.2). 一个简单的非匿名解决方案

(1.3). 一个非对称均衡

(2). 彩票支付规则的对称均衡

(2.1). 考虑大的 nn

(3). 证明者市场成本最小化

(3.1). 优化至少一个参与者

(3.2). 渐近线

(3.3). 1 + \ln c1+lnc 界限是紧的

(4). 工作量证明目标函数

(4.1). 渐近线

(5). 结论与未来工作

(5.1). 替代成本函数

(5.2). 异质代理与信息不对称

(5.3). 代币、空投与区块链应用

---

1. 动机与模型

开场小品 – 你在你当地的体育酒吧，并有一张桌子观看 NBA 季后赛。你不想独自观看，因此你计划让群聊知道你在那里。为了让人们更愿意来，你主动提出购买第一轮鸡翅，但你首先需要决定订购多少。如果你订购的太少，则可能没有人出现，因为他们认为其他人会去，并且鸡翅不够分。如果你订购的太多，如果每个人都来，桌子会没有空间。购买多少鸡翅才是最佳数量，以便你的一些朋友来，但不是全部？ ^11

这个故事经常出现在区块链协议设计中。协议希望以某种形式吸引参与，并使用激励措施来引出它：

• 工作量证明提供区块奖励，以激励矿工解决密码难题。
• 权益证明提供共识奖励，以用于正确地质押和投票区块。
• 证明者市场协调计算密集型 ZK 证明的生成。

至关重要的是，区块链还希望允许无需许可的参与。这使得协调问题更加困难。本文提出了一个激励参与的模型，并分析了匿名、共同价值支付规则的对称均衡。特别是，我们研究了每个参与者都以概率 pp 购买彩票的混合策略的均衡。

1.1. 参与博弈模型

我们将参与博弈建模如下：

• 参与者 – 参与者是一个战略代理，可以根据机制选择购买入场券。
• 参与者 – 参与人是指购买入场券的参与者。
• 协议 – 协议是一个具有成本函数（或等效地，一个正估值函数）的代理，用于诱导参与。
• 支付规则 – 一种由协议实现的函数，将参与者集合映射到他们各自的支付。

假设参与博弈中有 nn 个参与者。每个人都面临着相同的入场费 qq，为了简单起见，我们对本文的其余部分使用 q=1q=1。每个参与者都可以确定性地决定加入或不加入；他们也可以选择玩一种随机策略，即以某种概率 pp 加入。在决定是否加入之前，参与者会观察协议指定的支付规则。支付规则可以取决于已实现的参与者集合，并且可以是随机的。每个参与者选择一个行动来最大化他们的预期效用，这意味着他们收到的预期支付减去入场费（如果他们选择参与）。

以下两节介绍了匿名性和对称性的概念。

1.2. 一个简单的非匿名解决方案

假设协议旨在吸引至少一个参与者，并假设参与者偏向于参与。一个简单的机制如下：“选择一个特定的参与者，表示为 WINNER，并告诉他们，如果他们参与，你将支付他们 $1。”这个简单的解决方案具有许多理想的属性：

1. 对每个人而言都具有个人理性（因为每个参与者都可以通过不参与来获得零效用），并且
2. 在均衡中令人满意的参与（WINNER 将参与，而其他人不会），并且
3. 为协议支付最小化（因为 $1 是票价，因此是获得参与者的最小可能成本）。

如果协议设计者可以接受选择一个获胜者，那么这个解决方案就足够了。^22 我们不会在此止步，而是专注于一组匿名解决方案。

定义 (非正式): 匿名支付规则不能取决于参与者的身份。

我们在第 3.3 节中形式化了此属性，但希望它应该是直观的。这些支付规则必须平等地对待每个参与者。这些规则可以取决于参与者的行为（例如，通过在所有参与者之间平均分配奖金），并且可以是随机的（例如，通过随机地将奖金给予单个参与者）。但是，上述机制依赖于参与者的身份，并且不是匿名的。

1.3. 一个非对称均衡

另外，考虑以下情况：“一个参与者，表示为 COMMITTER，公开承诺购买票并成为参与者。”根据支付规则，此承诺可能会阻止其他参与者参与。例如，假设支付规则在所有参与者之间平均分配 $1 的奖金。在这种情况下，考虑加入的第二个参与者肯定会获得负效用，因为他们支付 $1 并赚取 $1/2。这导致没有人加入该协议，并且 COMMITTER 赚取了全部奖金。对于该协议而言，此均衡是支付最小化的，但需要参与者选择 COMMITTER，从而将协调复杂性推给参与者。我们使用此示例来限制我们将注意力集中在对称均衡。

定义： 在对称均衡中，每个参与者都使用相同的策略。

此策略可以是确定性的（例如，始终购买票并参与）或混合的（例如，以概率 pp 购买票）。由于这些确定性策略可以分别被认为是 p=0p=0 或 p=1p=1，因此任何对称均衡都由单个值 p\in[0,1]p∈[0,1] 完全指定。在这种均衡中，参与者的数量是从 \text{Binomial}(n,p)Binomial(n,p) 中抽取的，其中 nn 是参与者的数量。

2. 彩票支付规则的对称均衡

由于我们的注意力仅限于对称均衡，因此参与者的策略只有三种结果：

1. 没有人加入 (p=0p=0)，
2. 每个人都加入 (p=1p=1)，
3. 每个人都以概率 p\in (0,1)p∈(0,1) 加入。

根据支付规则，任何这些结果都是可能的。本节研究彩票支付规则。

定义： 彩票支付规则通过从参与者集合中统一随机选择一个获胜者，向单个参与者支付大小为 xx 的奖金。

彩票支付规则是匿名的，并根据 xx 的大小诱导对称均衡 pp。协议设置 xx 的值，参与者决定是否加入，并且奖金全额授予其中一位参与者。如果 x<1x<1，则我们处于情况 (1)；没有人会加入，因为奖金小于入场费。如果 x\geq nx≥n，那么我们处于情况 (2)；每个人都会参与，因为他们保证（在预期中）获得的报酬高于入场费。对于 xx 的其他值，参与者的数量将是从 \text{Binomial}(n,p)Binomial(n,p) 中抽取的随机变量，其中 p\in (0,1)p∈(0,1)。协议可以通过调整 xx 来移动平均值 npnp。

我们可以描述上述情况 (3) 下的对称均衡，其中每个参与者混合他们的策略并以概率 pp 加入。（有很多方法可以做到这一点；我们在这里显示显式的方法，使用微分；有关替代方法，请参见附注#1。）我们通过将其他参与者的策略固定为 pp，来考虑参与者 ii 的决策。ii 选择其加入概率 p'p′ 以最大化其预期效用，

\begin{align}
U_i(p') &= \bigg[ \underbrace{\mathbb{E}\left[\frac{x}{1+Y}\right]}_{\text{expected winnings}} - \underbrace{1}_{\text{ticket price}}\bigg] p', \; \text{where } Y \sim \text{Binomial}(n-1,p) \\\
&= \left[x\cdot \frac{1-(1-p)^n}{np} -1\right]p'
\end{align}

Ui(p′)=[E[x1+Y]预期收益−1票价]p′,where Y∼Binomial(n−1,p)=[x⋅1−(1−p)nnp−1]p′

换句话说，如果参与者 ii 加入并在参与者中赢得彩票，则她将获得 xx 的报酬。特别是，由于其他 n-1n−1 个参与者中的每一个都以概率 pp 独立加入，因此 ii 之外的参与者人数是从 \text{Binomial}(n-1,p)Binomial(n−1,p) 中抽取的。加入的效用是该支出减去票价。以概率 p'p′ 加入的效用是她加入的效用乘以 p'p′，因为 ii 从不加入获得 0 效用。

对于对称策略 pp 成为均衡，p'=pp′=p 必须在所有 p'\in[0,1]p′∈[0,1] 中最大化此表达式。一阶条件是

\begin{align}
\frac{\partial U_i}{\partial p'} = x\cdot \frac{1-(1-p)^n}{np} -1.
\end{align}

∂Ui∂p′=x⋅1−(1−p)nnp−1.

将其设置为零，我们得到 xx 和 pp 之间关系的解析解，

x\cdot \frac{1-(1-p)^n}{np} -1 = 0\implies \boxed{x = \frac{np}{1-(1-p)^n}}

x⋅1−(1−p)nnp−1=0⟹x=np1−(1−p)n

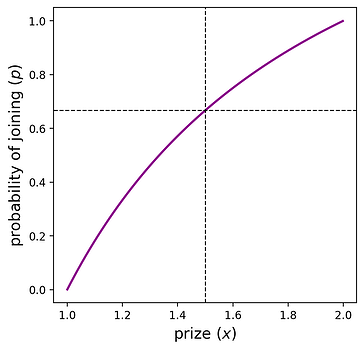
这告诉我们：“给定大小为 xx 的奖金，什么概率 pp 会产生对称均衡”，或者等效地，“如果协议设计者希望参与者数量来自 \text{Binomial}(n,p)Binomial(n,p)，则他们设置大小为 xx 的奖金”。下图显示了 n=2n=2 时这些变量之间的关系。

\ upload_d625b6de301ed0283341dc168f71222a931×895 37.7 KB

虚线可以解释为“如果协议设置奖金 x=1.5x=1.5，那么策略 p=2/3p=2/3 是对称均衡”。另外，请注意，如果奖金 <1<1 或 >2>2，则参与者分别以概率 0 或 1 加入。这些是本节开头描述的“没有人加入”和“每个人都加入”的结果。对于内部区域，x \in (1,2)x∈(1,2)，每个 xx 都会诱导唯一的 pp。

附注 #1 推导出相同方程的另一种方法是考虑所有参与者的总现金流。对于给定的 pp，参与者在预期的入场费中支付 npnp。因此，协议将需要在预期中支付 npnp 作为补偿（因为这是一个竞争均衡，任何超额价值都将被竞争掉）。当协议选择奖金 xx 时，只要至少有一个参与者参与，参与者集合就会收到此奖金。这以概率 1-(1-p)^n1−(1−p)n 发生，这意味着参与者集合在奖励中赚取 x \cdot (1-(1-p)^n)x⋅(1−(1−p)n)。

附注 #2： 混合策略均衡的一个有趣的特性是，参与者对任一行动都无动于衷（这就是他们首先随机化其行为的原因）。在上面的示例中，如果其他每个人都以概率 pp 加入，则参与者 ii 从任何行动中都获得零效用。你可以通过将 xx 代入她的效用函数来看到这一点，

\begin{align}
U_i(p') &= \bigg[ x \cdot \frac{1-(1-p)^n}{np} -1\bigg] \cdot p' \\\
&= \bigg[\frac{np}{1-(1-p)^n}\cdot \frac{1-(1-p)^n}{np} -1\bigg] p' \\\
&= (1-1)p'\\\
&= 0.
\end{align}

Ui(p′)=[x⋅1−(1−p)nnp−1]⋅p′=[np1−(1−p)n⋅1−(1−p)nnp−1]p′=(1−1)p′=0.

解释的另一种方式是，均衡是完全竞争的。这导致了结果之间的漠不关心和由此产生的混合策略。

2.1 考虑大的 nn

回想一下关系

x = \frac{np}{1-(1-p)^n}.

x=np1−(1−p)n.

关于这个方程的一个有趣的观察是，对于大的 nn，我们可以使用 (1-x) \rightarrow e^{-x}(1−x)→e−x（对于小的 xx）将 xx 重写为 \mu=npμ=np（参与者的预期数量）的函数，如

x(\mu) \approx \frac{\mu}{1-e^{-\mu}}.

x(μ)≈μ1−e−μ.

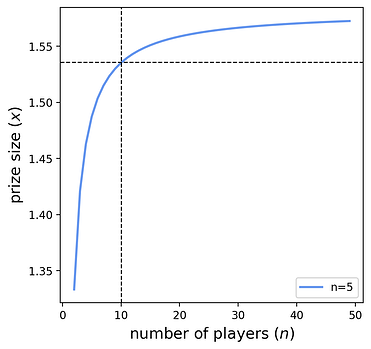
协议可以使用这个简单的公式来定位所需的平均参与计数 \muμ，而无需知道 nn。例如，如果协议希望在预期中有一个参与者，则它应将奖金设置为 1/(1-1/e)\approx 1.5821/(1−1/e)≈1.582。也就是说，协议支付超过 11 的入场费 58\% 的溢价，以吸引预期中的一名参与者。随着 nn 的增长，此近似值会提高。下图显示了吸引平均一名参与者所需的协议奖金。它还显示了当 n \to \inftyn→∞ 接近 x(1)=1/(1-1/e)x(1)=1/(1−1/e) 时的限制。

\ upload_9cde4a87098e4108fb332832c204d531949×895 33.3 KB

虚线可以解释为：“如果 n=10n=10，那么协议设计者需要设置至少 x=1.535x=1.535 的奖金才能吸引预期中的一名参与者。”当然，协议设计者可能会选择更高的奖金，以降低没有参与者的风险。以下部分正式描述了这种权衡。

3. 证明者市场成本最小化

到目前为止，我们已经展示了协议如何通过改变 xx 来定位特定的预期参与计数 \muμ。我们现在考虑特别厌恶低参与度的协议。我们通过引入“低参与度惩罚”来形式化这一点。在本节中，我们首先检查证明者市场。在第 4 节中，我们将研究由工作量证明共识推动的不同低参与度惩罚。

我们考虑一个 ZK Rollup，它希望激励昂贵的证明生成。市场设计者可能只关心至少 1 个证明者参与（并支付入场费，即生成证明的成本）。^33 此外，假设如果没有参与，协议可以自行生成证明，成本为 cc（你可以将 cc 视为“外部选项”）。这使我们可以将低参与度惩罚写为参与者数量 kk 的函数，如

\begin{align}
\text{low-participation penalty}(k) =
\begin{cases}
c & \text{if } k = 0 \\\
0 &\text{otherwise}.
\end{cases}
\end{align}

low-participation penalty(k)={cif k=00otherwise.

自然地，协议设计者希望选择一种支付规则，以最大限度地降低其总成本（奖金大小加上任何惩罚）。

3.1. 优化至少一个参与者

以上分析允许协议设计者选择奖金的大小，以在由 xx 和 pp 之间的关系诱导的对称均衡下定位一定数量的参与度。通过低参与度惩罚，协议的成本函数（我们用 C_pCp 表示），为

C_p = c \cdot \Pr[\text{no participation}] + x \cdot \Pr[\text{participation}].

Cp=c⋅Pr[没有参与]+x⋅Pr[参与].

此成本是协议试图最小化的成本，并且在给定 cc 时，协议在选择 xx 时面临权衡。xx 的值太低会导致协议以高概率产生惩罚 cc；xx 的值越高，成本就越高，因为协议必须支付更大的奖金。使用在对称均衡中每个参与者都以概率 pp 参与的事实，我们可以写成，

C_p = c \cdot (1-p)^n + x \cdot (1-(1-p)^n).

Cp=c⋅(1−p)n+x⋅(1−(1−p)n).

使用 x = \frac{np}{1-(1-p)^n}x=np1−(1−p)n（我们上面推导出的关系），这简化为

C_p = c \cdot (1-p)^n + np.

Cp=c⋅(1−p)n+np.

这是协议成本，它试图在 p \in [0,1]p∈[0,1] 上最小化。通过最佳概率 p^*p∗，协议可以直接计算出在 p^*p∗ 处诱导对称均衡所需的奖金大小。我们使用一阶条件来最小化协议的成本，

\begin{align}
\frac{\partial C_p}{\partial p} &= -cn(1-p)^{n-1} + n =0 \\\
&\implies p^* = 1-c^{-\frac{1}{n-1}}
\end{align}

∂Cp∂p=−cn(1−p)n−1+n=0⟹p∗=1−c−1n−1

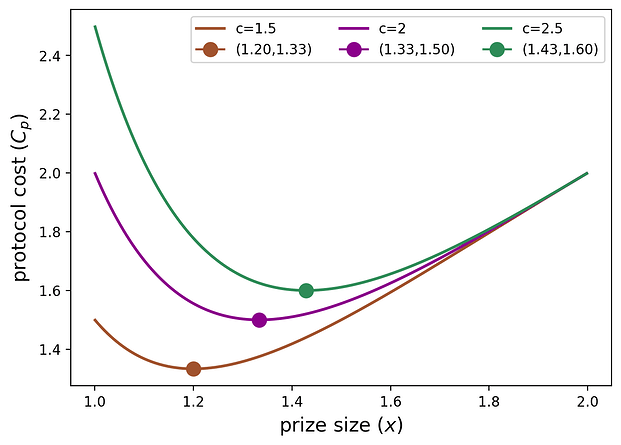
二阶导数在 p \in [0,1]p∈[0,1] 上始终为负，因此 p^*p∗ 确实是协议成本的唯一局部最小值。下图显示了协议成本作为 xx 的函数（这与 n=2n=2 和 c=1.5,2,2.5c=1.5,2,2.5 的 p\in(0,1)p∈(0,1) 具有双射关系）。

\ upload_68cf7e34e09faa5dfee6d7ce96b8e0fb1246×895 62.3 KB

x^*x∗ 值（在图中表示为点）随着 cc 的增加而增加，因为当协议因没有参与而面临更高的惩罚时，它会选择更高的 x^*x∗（这会导致更高的 p^*p∗）以非常有信心至少一名参与者会参与。从 p^*p∗ 中，我们以闭合形式计算出最佳奖金大小，如

\begin{align}
x^* &= \frac{np^*}{1-(1-p^*)^n} \\\
&= \frac{n(1-c^{-1/(n-1)})}{1-c^{-n/(n-1)}}
\end{align}

x∗=np∗1−(1−p∗)n=n(1−c−1/(n−1))1−c−n/(n−1)

我们还计算出最佳协议成本为

\begin{align}
C_p^* &= c \cdot (1-p^*)^n + np^* \\\
&= n-(n-1) c^{-1/(n-1)}
\end{align}

C∗p=c⋅(1−p∗)n+np∗=n−(n−1)c−1/(n−1)

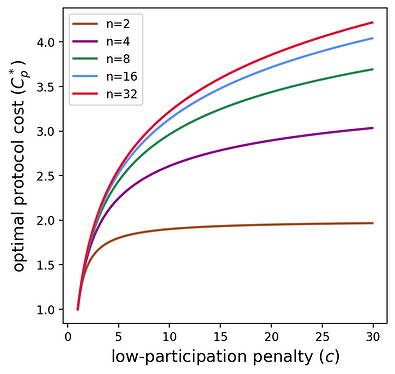
下图有助于将此成本可视化为 n,cn,c 的函数。

\ upload_32974a3ccb2b0fc03b6c63af46b5baa4945×895 66.1 KB

我们看到，随着低参与度惩罚的增加，协议成本似乎呈对数比例增长。下一节通过查看协议成本的渐近行为来形式化这种关系。

3.2 渐近线

一个自然的问题是，p^*, x^*, C_p^*p∗,x∗,C∗p 的值如何作为 cc 的函数进行缩放。特别是，假设博弈中有大量的参与者 nn，协议设计者可能想知道他们的效用如何作为 cc 的函数进行缩放。展开（有关推导，请参见脚注 ^44），我们得到

\begin{align}
p^* &= \frac{\ln c}{n-1} + O\left(\frac{(\ln c)^2}{n^2}\right).
\end{align}

p∗=lncn−1+O((lnc)2n2).

同样，我们可以检查 x^*x∗ 的渐近行为（有关推导，请参见脚注 ^55），这是成本最小化协议的最佳奖金：

\begin{align}
x^* = \frac{\ln c}{1 - 1/c} + O\left(\frac{(\ln c)^2}{n}\right).
\end{align}

x∗=lnc1−1/c+O((lnc)2n).

最后，我们检查协议支付的最佳成本 C_p^*C∗p 的渐近行为（有关推导，请参见脚注 ^66）：

\begin{align}
C_p^* &=1 + \ln c + O\left(\frac{(\ln c)^2}{n}\right).
\end{align}

C∗p=1+lnc+O((lnc)2n).

至关重要的是，我们看到，随着 n\to\inftyn→∞，协议的总成本按 1+ \ln c1+lnc 缩放。这对于协议来说是好消息，因为它提供了成本作为外部选项函数的对数界限。此外，最佳成本不取决于 nn。这在无需许可的环境中非常有用，因为协议可以仅根据外部选项（即低参与度惩罚）的质量来设置最佳奖金，而无需知道有多少参与者！这也意味着，即使博弈中的参与者数量非常大，协议也可以确保其成本是有界的。^77 下一节回答了这个问题，“我们能突破这个对数界限吗？” 更正式地说，是否存在匿名支付规则，使得由此产生的对称均衡具有协议成本 C_p < 1+\ln cCp<1+lnc？ 我们将在下一节中证明答案是否！ 协议成本被严格限制在 1+\ln c1+lnc。

3.3 1+\ln c1+lnc 界限是紧的

注意：对于数学/形式主义反感的人群，可以安全地跳过本节！

我们知道在对称均衡中，每个参与者都以概率 pp 加入。我们需要将我们在第 1.2 节中概述的匿名性属性形式化，以便将我们的机制与其他匿名支付规则进行比较。支付规则 \pi(S,r)π(S,r) 接受已加入的参与者集合 S\subseteq [n]S⊆[n] 和一个随机种子 rr 作为输入，并输出给每个参与者的支付。上一节中的机制以 1/|S|1/|S| 的概率向随机参与者支付彩票奖金 xx（如果 SS 非空），否则不支付任何人。如果一个机制 \pi(S,r)π(S,r) 在参与者的行为方面是逐点对称的，我们就说它是（事后）匿名的。形式上，如果对于所有 rr 和 SS 以及所有排列 \sigmaσ，\pi(S,r)=\pi(\sigma(S),r)π(S,r)=π(σ(S),r)，则 \piπ 是事后匿名的。当一个机制是匿名的时候，我们可以将其支付规则重写为 \pi(S,r)=\pi(k,r)π(S,r)=π(k,r)，其中 k=|S|k=|S|，并且是从 \text{Binom}(n,p)Binom(n,p) 中抽取的。现在我们只关心参与者的数量，而不是具体的集合。

设 \pi(k,r)π(k,r) 是一个具有对称均衡 pp 的匿名机制。那么，拍卖人的预期成本是

C_p = \underbrace{c \cdot (1-p)^n}_{\text{无人参与}} + \underbrace{\mathbb{E}_{k,r}[\pi(k,r)]}_{\text{有人参与}}.

Cp= \underbrace{c \cdot (1-p)^n}_{\text{无人参与}} + \underbrace{\mathbb{E}_{k,r}[\pi(k,r)]}_{\text{有人参与}}.

这个期望是关于随机性实现 rr 和每个可能的参与者数量 kk 的。在期望中，我们知道每个 kk 参与者必须单独理智才能加入彩票。总的来说，任何协议必须至少支付每个参与者的报名费的期望值。形式上，\mathbb{E}_{k,r}[\pi(k,r)] \geq np.Ek,r[π(k,r)]≥np. 将其代入，我们再次得到以下形式

C_p \geq c \cdot (1-p)^n + np.

Cp \geq c \cdot (1-p)^n + np.

在等式上，这正是彩票机制的协议成本。因此，它具有相同的最佳协议成本 C_p^* = n-(n-1) c^{-1/(n-1)}C∗p=n−(n−1)c−1/(n−1)，并且当 n \to \inftyn→∞ 时，具有 1+\ln c1+lnc 的渐近行为。在最小化“至少一名玩家”的目标中，彩票机制在匿名和单独理性的机制中是最优的！

4. 工作量证明目标函数

在前一节中，协议仅在无人参与的情况下才会产生成本 cc。这对应于参与者数量 kk 中的以下阶跃函数，

\begin{align} \text{低参与度惩罚}(k) = \begin{cases} c & \text{如果 } k = 0 \\ 0 &\text{其他情况}. \end{cases} \end{align}

\begin{align}
\text{低参与度惩罚}(k) =
\begin{cases}
c & \text{如果 } k = 0 \\\
0 &\text{其他情况}.
\end{cases}
\end{align}

对于证明者市场示例，这种成本函数是有意义的，因为只需要一个参与者，因为只需要一个证明就可以满足协议。在其他区块链环境中，不同的低参与度惩罚（或一般的参与估值函数）可能更有意义；例如，工作量证明需要来自许多矿工的参与。我们的参与框架也可以应用于这些更一般的场景。直观地说，我们以下列方式拆分协议成本

C_p : \text{低参与度惩罚} + \text{用于激励参与的奖励}.

Cp: \text{低参与度惩罚} + \text{用于激励参与的奖励}.

不同设置中的不同参与要求将对应于不同的第一项。在彩票奖励机制中，第二项始终是 npnp（即，我们在此处使用的支付规则，通过与第 3.3 节中的论点类似的论点，该规则是最优的）。

为了证明通用性，我们选择了另一个能够体现工作量证明挖矿精神的惩罚函数：如果少于 50% 的玩家参与，则协议会受到惩罚。同样，这可以写成一个阶跃函数，其中产生惩罚的阈值从 0 个参与者提高到少于 n/2n/2 个参与者，

\begin{align} \text{PoW 低参与度惩罚}(k) = \begin{cases} c & \text{如果 } k < n/2 \\ 0 &\text{其他情况}. \end{cases} \end{align}

\begin{align}
\text{PoW 低参与度惩罚}(k) =
\begin{cases}
c & \text{如果 } k < n/2 \\\
0 &\text{其他情况}.
\end{cases}
\end{align}

如果至少 50% 的玩家选择参与，那么该协议可以确保没有恶意行为者能够获得足够的哈希算力来对网络进行 51% 攻击。这是一种表示工作量证明协议可能试图诱导的参与类型的方式。^88 与之前一样，为了吸引参与，该协议指定一个彩票奖金，从而产生每个玩家都以概率 pp 混合的对称均衡，并且我们具有熟悉的关系，x = \frac{np}{1-(1-p)^n}x=np1−(1−p)n. 因此，总协议成本可以写成，

\begin{align} C_p = c \cdot \Pr[k < n/2] + np, \quad k \sim \text{Binom}(n,p). \end{align}

\begin{align}
C_p = c \cdot \Pr[k < n/2] + np, \quad k \sim \text{Binom}(n,p).
\end{align}

我们可以将其展开为

\begin{align} C_p = c \cdot \sum_{k=0}^{n/2} \binom{n}{k}p^{k}(1-p)^{n-k} + np. \end{align}

\begin{align}
C_p = c \cdot \sum_{k=0}^{n/2} \binom{n}{k}p^{k}(1-p)^{n-k} + np.
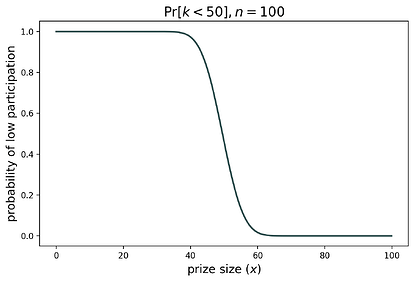
\end{align}

对于 n=100n=100 个玩家，下图显示了对于各种奖金大小 xx，参与者数量 k<50k<50 的概率（因此协议会产生 PoW 低参与度惩罚）。

\ upload_54c70df9f2113debd9038344ddb43a1d1392×947 43.6 KB

有三种情况：

1. 小奖金： 当奖金为 x\in[0,40]x∈[0,40] 时，由此产生的 pp 的均衡值将很低，因此 k < 50k<50 几乎是必然的。
2. 中等奖金： 当奖金为 x\in (40,60)x∈(40,60) 时，由此产生的 pp 的均衡值足够大，以至于在 k<50k<50 和 k>50k>50 这两个事件上都存在显着的概率质量。
3. 大奖金： 当奖金为 x\in[60,100]x∈[60,100] 时，由此产生的 pp 的均衡值将很高，因此 k<50k<50 几乎永远不会发生。

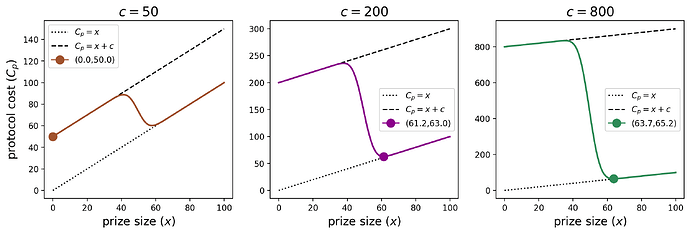
这三种情况决定了协议面临的总成本。下图显示了当 n=100n=100 时，协议成本作为 x \in [0,100]x∈[0,100] 的函数，对于 cc 的各种值。

\ upload_b3fe4e4ad23a1b198278421596e29ab42340×795 104 KB

我们看到协议成本在 xx 中是非单调的：

• 从 x= 0 \nearrow 40x=0↗40 我们看到 C_pCp 增加。当 x=0x=0 时，没有人参与 (p=0p=0)，协议成本为 cc。随着 xx 增加到 40，pp 仍然很小，这意味着 \Pr[k < n/2] \approx 1Pr[k<n/2]≈1，并且协议几乎肯定必须支付 cc 惩罚以及 xx。这可以用直线 x+cx+c 来近似（上图中用虚线表示）。
• 从 x \approx 40 \nearrow 60x≈40↗60 我们看到 C_pCp 减少。协议仍然在支付不断增加的奖金 xx，但现在 \Pr[k < n/2]Pr[k<n/2] 上的概率质量显着减少，因此在预期中，协议支付 cc 的频率较少。
• 从 x \approx 60 \nearrow 100x≈60↗100 我们看到 C_pCp 再次增加。在这些 xx 值下，\Pr[k < n/2] \approx 0Pr[k<n/2]≈0，协议几乎永远不必支付成本 cc。继续增加 pp 不再边际上值得增加 xx 的成本。这种情况下的成本可以用直线 xx 来近似（上图中用点线表示），因为协议成本与奖金规模呈线性增加。

如上图所示，曲线的形状保持不变，但是端点行为和局部最小值取决于 cc 的值。圆形标记显示了分别使 c=50,200,800c=50,200,800 的协议成本最小化的 x^*x∗。对于 c=50c=50，最佳奖金规模为 x^*=0x∗=0，这意味着没有激励参与，协议只是支付低参与度惩罚。相反，对于 c=200,800c=200,800，最佳奖金规模位于 (0,100)(0,100) 的内部，这意味着该协议诱导一些，但不是全部参与。

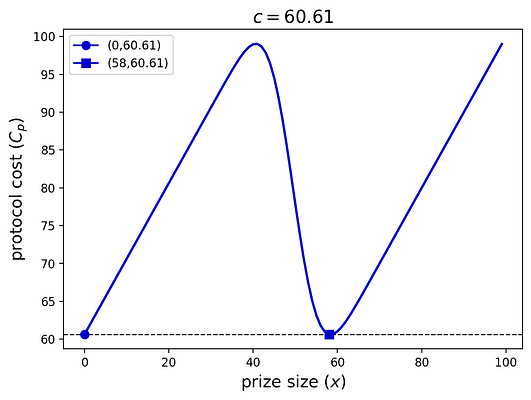
下图显示了一个有趣的 cc 值，其中协议在支付低参与度惩罚或通过设置 x^*=58 来激励参与之间无差异。x∗=58.

\ upload_5fad06e6387e2cdf634143842df251a01255×945 61.3 KB

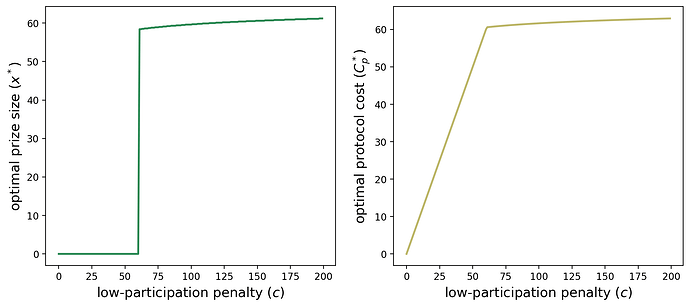
在任何一种情况下，最佳协议成本都是 C_p^*=60.61C∗p=60.61，因为在 x^*=0,58x∗=0,58 处都存在最小值。这是该协议开始激励参与的地方（通过从 x=0x=0 切换到 x>0x>0 的值）。下图显示了最佳奖金和协议成本作为 cc 的函数。

\ upload_5d69ebd40f9b12718be9e847b0c73ac92013×895 63.7 KB

我们看到了在 c= 60.61c=60.61 处具有临界值的不同情况。对于 c < 60.61c<60.61，协议成本线性增加，因为整个情况下的最佳 xx 是 x^*=0x∗=0；协议始终选择不激励参与并支付惩罚 cc。对于 c>60.61c>60.61，协议成本增加得慢得多，因为最佳 xx 诱导了大量的参与，这意味着几乎永远不会支付 cc 的低参与度惩罚。对于更大的 cc 值，我们看到了一种新的情况，其中 C_p^*C∗p 似乎缩放得非常缓慢。我们没有最佳 x^*x∗ 的封闭形式（因为它是 n 次多项式的解），但是我们可以近似 cc 增加时的渐近行为。

4.1 渐近线

在深入研究渐近线之前，值得注意的是，我们选择 50% 的值只是出于工作量证明的动机。成本函数的更通用形式可以取决于任何（常数）\alpha \in [0,1]α∈[0,1]，其中协议试图激励至少 \alphaα 部分候选人的参与：

\begin{align} \text{低参与度惩罚}(k,\alpha) = \begin{cases} c & \text{如果 } k < n \alpha \\ 0 &\text{其他情况}. \end{cases} \end{align}

\begin{align}
\text{低参与度惩罚}(k,\alpha) =
\begin{cases}
c & \text{如果 } k < n \alpha \\\
0 &\text{其他情况}.
\end{cases}
\end{align}

我们想研究在通用 \alphaα 参与成本函数下，最佳协议成本的行为，该成本在求解以下的 p^*p∗ 处实现：

\begin{align} \min_{p \in [0,1]} C_p = c \cdot \Pr[k < n \alpha] + np, \quad k \sim \text{Binom}(n,p). \end{align}

\begin{align}
\min_{p \in [0,1]} C_p = c \cdot \Pr[k < n \alpha] + np, \quad k \sim \text{Binom}(n,p).
\end{align}

我们无法显式求解 p^*p∗（以及 C_p^*C∗p）；相反，我们通过选择次优 pp 并使用该 pp 限制成本来给出协议成本的上限。

首先，我们给出一些直觉。假设协议设置 p=\alphap=α。那么，\Pr[k < n \alpha] =1/2Pr[k<nα]=1/2，因此协议在预期中支付惩罚 c/2c/2。此外，协议支付 \alpha nαn 大小的预期奖金（假设至少有一个参与者）。总体而言，协议成本将为 C_p\approx c/2+npCp≈c/2+np。此成本与 cc 呈线性关系，但是协议可以通过选择 p > \alphap>α 来减少预期中的惩罚项来做得更好。通过选择更高的 pp，协议可以减少其在惩罚上的支出，但会增加其在奖金上的支出。我们将选择一个使预期惩罚保持不变的 pp，并使用该 pp 来限制总体成本。

使用关于 k < \alpha nk<αn 概率的 Chernoff 界限，

\begin{align} \Pr[k < n \alpha] \leq e^{-n(p-\alpha)^2/(2p)}. \end{align}

\begin{align}
\Pr[k < n \alpha] \leq e^{-n(p-\alpha)^2/(2p)}.
\end{align}

我们可以通过将右侧设置为 1/c1/c，来使预期中的低参与度惩罚保持不变：

p' := \alpha + \frac{\ln c}{n} \left(1 + \sqrt{1+ \frac{2\alpha n}{\ln c}}\right)

p' := \alpha + \frac{\ln c}{n} \left(1 + \sqrt{1+ \frac{2\alpha n}{\ln c}}\right)

然后，我们将完整协议成本设为

\begin{align} C_p^* = \min_{p\in[0,1]}C_p &\leq c \cdot\Pr[k < \alpha n] + np' \\ &\leq 1+ n\left(\alpha + \frac{\ln c}{n} + O(\sqrt{\alpha\ln c /n})\right) \\ &= 1 + \alpha n + \ln c + O(\sqrt{\alpha n \ln c}). \end{align}

\begin{align}
C_p^* = \min_{p\in[0,1]}C_p &\leq c \cdot\Pr[k < \alpha n] + np' \\\
&\leq 1+ n\left(\alpha + \frac{\ln c}{n} + O(\sqrt{\alpha\ln c /n})\right) \\\
&= 1 + \alpha n + \ln c + O(\sqrt{\alpha n \ln c}).
\end{align}

我们可以直观地将此限制视为如下。第一项 (1) 是预期的、常数的低参与度惩罚（通过构造）。表达式的其余部分是参与者的预期付款。对于吸引至少 \alpha nαn 参与（以补偿报名费）的任何协议，\alpha nαn 项是不可避免的。其余项是协议为避免支付低参与度惩罚而产生的额外付款。

让我们将其与证明者市场设置进行比较，其中 1 的低参与度阈值在此处对应于 \alpha=1/nα=1/n。回想一下，最佳成本的缩放比例为 1+ \ln c + O((\ln c)^2/n).1+lnc+O((lnc)2/n). 将 \alpha=1/nα=1/n 插入到我们的新界限中，我们得到协议成本的较宽松界限 2+\ln c + O(\sqrt{\ln c})2+lnc+O(√lnc)。这些在渐近线上匹配，但在误差项中有所不同。我们怀疑此渐近界限对于任何 \alpha > 1/nα>1/n 都是严格的（例如，通过正确的反浓度不等式或使用二项式的正态近似）。同样，我们怀疑与 第 3.3 节 中使用的推理类似的推理可以显示彩票支付规则对于工作量证明协议成本的最优性。我们在此帖子中省略了这些技术细节。

5. 结论和未来工作

到目前为止，我们学到了什么？我们以有关如何激励无许可参与的问题开头，并将我们的范围限制为具有彩票支付规则的参与博弈的对称、匿名均衡。第 2 节 探讨了奖金 XX 与每个玩家用作其混合策略的最终均衡概率 PP 之间的关系。 第 3 节 介绍了由证明者市场驱动的低参与度惩罚的概念，在该市场中，协议需要至少一个参与者才能避免支付外部选项成本。我们在此目标下得出了最佳彩票奖金，并表明彩票机制是最佳支付规则。 第 4 节 探讨了一种由工作量证明驱动的不同协议参与目标，在该目标中，协议需要 50% 玩家的参与。在我们继续之前，值得强调的是，如何扩展该模型以涵盖更现实的设置。

5.1 替代成本函数

在此帖子中，我们研究了针对以下目标进行优化的成本函数

• 至少一位参与者，以及
• 至少 \alpha nαn 位参与者（对于常数 \alphaα）。

这两个程式化的协议目标函数都是一种更普遍现象的特定实例。想象一下，一组更具表现力的“参与估值函数”，它们不在我们一直在使用的阶跃函数族中。例如，对于 kk 位参与者，该协议可以表达 c\cdot e^{-k}c⋅e−k 的偏好（或任何其他对参与度提高具有边际收益递减的功能形式）。在这种情况下，协议需要一定的参与度（例如，如果没有人参与，则会受到 cc 的惩罚），但是第 k+1^{st}k+1st 位参与者加入的边际价值呈指数衰减。

无论确切的协议目标如何，此框架都使我们能够量化实现协议最佳结果所需的最佳彩票奖金规模。我们将回到最初的一组激励示例，并描述每个示例的备选协议目标。首先，我们讨论的两个：

• 证明者市场（如第 2 节所示） – 确保至少一位参与者提交证明，以避免产生可观的外部成本（例如，活性故障或团队自己运行证明者）。 或者，证明者市场设计者可能会明确针对多个参与者以实现鲁棒性或竞争（例如，Succinct 的证明竞赛）。
• 工作量证明（如第 3 节所示） – 确保 50% 的参与度，以避免外部参与者执行 51% 攻击的能力。 或者，可以通过估计全局计算的供应曲线，来针对较低的阈值进行调整，以达到特定的经济安全性美元金额。

当然，某些协议可能还希望阻止过多的参与。

• 权益证明 – 确保在 10% 到 50% 之间的 token 供应量被质押。此目标可以明确阻止超出某些阈值的参与。 质押协议可能希望降低质押率，以确保原生 token 保持其效用并且通货膨胀率保持在较低水平。

希望这些案例研究能够证明协议设计者如何专门针对特定类型的无许可参与。

5.2 异构主体和信息不对称

未来工作的另一个角度是扩展博弈中参与者的模型。我们假设每个参与者的进入成本完全相同，均为 1 美元。但是，在许多现实环境中，不同参与者的参与价值和成本差异很大。电力成本可能会使工作量证明挖矿在德克萨斯州盈利，但在纽约市却无利可图。质押池可能具有不同的资本成本或交易策略，从而导致权益证明参与的收益不同。未来的工作可能会通过考虑每个参与者的进入费不同来对这种异质性进行建模。除了参与成本和奖励之外，代理商可能还具有不同的风险偏好。我们对风险中立的参与者进行建模（如果奖金足够大，即使他们的支出不确定，他们也会在加入和不加入之间无动于衷）。相比之下，风险规避可能更准确，尤其是考虑到加密资产的波动性。

参与者的异质性与信息不对称密不可分，因为与协议设计者相比，参与者可以更好地了解自己的成本。例如，在证明者市场中，证明能力会根据每个证明者可用的硬件而有所不同，协议很难直接审核。这促使我们将模型扩展到私人价值设置，在该设置中，协议会从每个参与者那里征求投标，从而将我们从彩票转移到拍卖。在拍卖框架下，可以使用大量的拍卖理论文献来提出和回答有关激励兼容性、收入最大化、福利最大化、效率等的问题。例如，Tullock 竞赛描述了远期、私人估值、全额支付拍卖的均衡。

除了标准的拍卖框架之外，协议还可以通过需求增强来补贴供应，从而减少信息不对称。例如，Aleo 向参与者发布证明奖励，以解决 Aleo 自己创建的难题。这些难题可以用作证明能力可用性的可信信号，这对于处理需求高峰是必需的。尽管 Aleo 的难题是人为生成的，但更有效的设计可以利用实际用户需求。例如，Ritual 使计划事务具有可预测的节奏，从而使其成为持续需求来源的良好候选者。促进这些持续的需求流可以用作支持网络的硬件的“可用性预言机”。

5.3 Tokens、空投和区块链应用程序

我们花了这篇文章的时间来研究协议设计者如何通过提供奖金来激励参与。当然，此奖金可以用美元计价，并有效地补贴供应商的成本。Uber 通过直接补贴来启动其平台供应商参与网络（例如，向驾驶员支付的费用高于向乘客收取的费用）。在区块链环境中，此奖励通常以协议特定的 token 计价；这类似于 Uber 通过向驾驶员授予股权来补贴乘车费用。同样，目标是启动，并且 token 补贴会预先提取需求以诱导供应，同时稀释 token 池。

空投是另一种补贴形式，重点是需求方。空投机制还通过奖励人们使用该协议来预先提取需求以促进平台增长。实际上，token 发行者会稀释自己，希望平台增长会使其 tokens 比没有发生用户补贴时更有价值。

激励无许可参与对于区块链按预期运行至关重要。我们希望这篇文章能够作为研究此类问题的起点，并提供一个有价值的模型来扩展。

---

_▓▒░ made with and markdown ◉ thanks for reading! – maryam & mike ░▒▓_

---

^11 有关此问题的一种变体，请参见El Farol Bar 问题。 ︎

^22 请注意，以上协议仅需要一位参与者。类似地，如果协议需要 k 位参与者，则可以指定总参与者池中大小合适的子集并支付其报名费。更一般而言，协议可以通过找到参与可以最大程度地降低协议成本的参与者子集，并承诺如果他们都加入，则偿还这些参与者（且仅这些参与者）的报名费，来优化任何目标函数。 ︎

^33 我们假设参与者具有同质的证明成本；协议设计者确切地知道此成本。将此推广到具有未知成本的异构证明者将成为未来帖子的主题。 ︎

^44 从 p^*p∗ 开始，我们重写，

p^* = 1-c^{-1/(n-1)} = 1-e^{-\ln c / (n-1)}.

p^* = 1-c^{-1/(n-1)} = 1-e^{-\ln c / (n-1)}.

使用 e^{-y}e−y 在 00 处且 y=\ln c / (n-1)y=lnc/(n−1) 的泰勒展开式，我们得到，

\begin{align} p^* &= 1 - \Big[\underbrace{1- y + \frac{y^2}{2} - \frac{y^3}{6} + \frac{y^4}{24} - \ldots}_{\text{expansion of $e^{-y}$}}\Big] \\ &= \frac{\ln c}{n-1} - \frac{(\ln c)^2}{2(n-1)^2} + \frac{(\ln c)^3}{6(n-1)^3} - \frac{(\ln c)^4}{24(n-1)^4} - \ldots \\ &= \frac{\ln c}{n-1} + O\left(\frac{(\ln c)^2}{n^2}\right). \end{align}

\begin{align}
p^* &= 1 - \Big[\underbrace{1- y + \frac{y^2}{2} - \frac{y^3}{6} + \frac{y^4}{24} - \ldots}_{\text{expansion of $e^{-y}$}}\Big] \\\
&= \frac{\ln c}{n-1} - \frac{(\ln c)^2}{2(n-1)^2} + \frac{(\ln c)^3}{6(n-1)^3} - \frac{(\ln c)^4}{24(n-1)^4} - \ldots \\\
&= \frac{\ln c}{n-1} + O\left(\frac{(\ln c)^2}{n^2}\right).
\end{align}

︎

^55 我们首先重写

\begin{align} x^* &= \frac{n(1-c^{-1/(n-1)})}{1-c^{-n/(n-1)}} =\frac{n\bigl(1 - e^{-\ln c/(n-1)}\bigr)}{1 - e^{-n\ln c/(n-1)}}. \end{align} x∗=n(1−c−1/(n−1))1−c−n/(n−1)=n(1−e−lnc/(n−1))1−e−nlnc/(n−1).

使用 e^{-y}e−y 在 00 处的泰勒展开，其中 y=\ln c / (n-1)y=lnc/(n−1)，我们有

\begin{align}
x^\* = \frac{n\bigl(1 - e^{-y}\bigr)}{1 - e^{-n y}} &= \frac{n(1-e^{-y})}{1-c^{-1}e^{-y}}\\\
&= \frac{n\displaystyle{y - \tfrac{y^2}{2} + \tfrac{y^3}{6} - \tfrac{y^4}{24} + \cdots}}
{\displaystyle{1-\tfrac1c (1-y+\tfrac{y^2}{2} - \tfrac{y^3}{6} + \tfrac{y^4}{24}+ \cdots)}} \\\
&= \frac{\displaystyle{ny + O\left(ny^2/2\right)}}
{\displaystyle{1-\tfrac1c +O(y/c)}}\\\\[6pt\]
&= \frac{\displaystyle \ln c + O\left(\frac{(\ln c)^2}{n}\right)}
{\displaystyle 1 -\frac1c+O\left(\frac{\ln c}{cn}\right)} = \frac{\ln c}{1 - 1/c} + O\left(\frac{(\ln c)^2}{n}\right).
\end{align}

x∗=n(1−e−y)1−e−ny=n(1−e−y)1−c−1e−y=ny−y22+y36−y424+⋯1−1c(1−y+y22−y36+y424+⋯)=ny+O(ny2/2)1−1c+O(y/c)=lnc+O((lnc)2n)1−1c+O(lnccn)=lnc1−1/c+O((lnc)2n).

︎

^66

\begin{align}
C\_p^\* &= n-(n-1) c^{-1/(n-1)} \\\
&= n- (n-1) e^{-\ln c / (n-1)}
\end{align}

C∗p=n−(n−1)c−1/(n−1)=n−(n−1)e−lnc/(n−1)

令 y=\ln c / (n-1)y=lnc/(n−1)，并再次使用 e^{-y}e−y 展开式，我们有

\begin{align}
C\_p^\*
&= n - (n-1)\Big\[1 - \frac{\ln c}{n-1} + \frac{(\ln c)^2}{2(n-1)^2} - \frac{(\ln c)^3}{6(n-1)^3} + \frac{(\ln c)^4}{24(n-1)^4} - \ldots\Big\] \\\
&= n - (n-1) + \ln c +O \left(\frac{(\ln c)^2}{n}\right) \\\
&=1 + \ln c + O\left(\frac{(\ln c)^2}{n}\right).
\end{align}

C∗p=n−(n−1)[1−lncn−1+(lnc)22(n−1)2−(lnc)36(n−1)3+(lnc)424(n−1)4−…]=n−(n−1)+lnc+O((lnc)2n)=1+lnc+O((lnc)2n).

︎

^77 此分析扩展到协议希望吸引的参与者不仅仅是一个，而是最多 \log clogc 个的情况。有关更大的参与需求，请参见第 4 节。︎

^88 根据我们如何定义参与博弈中的玩家集合，这种描述可能不会那么直观。例如，如果我们把玩家集合看作是可用于解决 PoW 难题的全球可用计算总和，那么诱导 50% 的参与可能有点过头了。我们使用这个例子是因为它很整洁，但需要对玩家的具体情况进行更多的建模，才能使这些结果具有实用性。︎

• 以太坊证明者市场提案

• 原文链接： ethresear.ch/t/on-incent...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～