调查比特币上各种脚本及签名方案，以及相关项目使用情况

大家都知道，比特币的脚本系统比以太坊或Solana等其他区块链更受限，它们更直接支持运行智能合约。尽管如此，许多人希望建立与比特币互操作的系统，部分原因是比特币是历史最悠久、持续时间最长的区块链。为了克服比特币的限制，人们将其脚本能力与其支持的签名方案属性相结合，以强加更高级别的属性，结合链上和链下的逻辑。

在这篇文章中，我们将简要看看比特币的脚本系统如何工作——包括其支持的签名方案和系统的发展——以及几个项目如何利用它们来构建在比特币中无法直接表达的功能。

比特币特性概述

首先，让我们看看比特币系统的一些关键元素，包括BIP-340 Schnorr签名、比特币的脚本虚拟机（VM）、常见的脚本类型如支付到公钥哈希（pay-to-pubkey hash）和支付到脚本哈希（pay-to-script hash）、脚本系统的扩展如SegWit版本0、Taproot脚本、契约（covenants），以及签名方案的扩展，FROST签名。

BIP-340 Schnorr签名

比特币使用数字签名来授权交易（或者更严格地说，使得签名的验证作为可以在授权交易的脚本中使用的原始条件）。

在Taproot升级之前，比特币仅使用椭圆曲线数字签名算法（ECDSA）签名。

从Taproot开始，它在某些上下文中还使用Schnorr签名。

这两种签名方案都使用Secp256k1椭圆曲线，其元素为256位（32字节）；它们都使用均匀随机的标量d作为私钥，并乘以固定生成元G生成公钥P；两者都需要对每条消息m签名一个独特的、均匀随机的秘密随机值k，但它们的签名和验证实现不同。

在以下伪代码中，n表示群组顺序，H表示哈希函数，字节字符串、整数模n和群组元素之间的类型转换被省略，许多良好性和奇偶性检查也被省略；完整细节，请参见比特币的ECDSA实现↗和比特币的Schnorr实现↗。

以下是ECDSA签名：

def sign_ecdsa(d, m, k):
    e = H(m)
    R = k*G
    r = R.x
    s = pow(k, -1, n)*(e + r * d)
    return (r, s)

def verify_ecdsa(P, m, sig):
    (r, s) = sig
    e = H(m)
    u1 = e*pow(s, -1, n)
    u2 = r*pow(s, -1, n)
    R = u1 * G + u2 * P
    return R.x == r

以下是Schnorr签名：

def sign_schnorr(d, m, k):
    P = d * G
    R = k * G
    e = H(R.x || P.x || m)
    s = k + e * d
    return (R.x, s)

def verify_schnorr(P, m, sig):
    (r, s) = sig
    e = H(r || P.x || m)
    R = s * G - e * P
    return R.x == r

两者的核心思想是，点R是对k的承诺，这一承诺是具有绑定性的（因为R是唯一由k决定的，G是固定的）并且是隐藏的（由于离散对数困难假设）。消息通过哈希为e进行承诺，然后通过一个针对椭圆曲线的标量场的方程将其转化为s，从而可以检查e是否是由仅包含承诺R和P确定的方程的唯一解，而无需知道k和d（相对于G，只有签名者知道R和P的离散对数）。对于Schnorr签名，这个方程是线性的；而对于ECDSA，这不是。

在拥有一对签名(sig1, sig2)和不同消息(m1, m2)的情况下，只要使用了相同的随机数k，就可以恢复出私钥d：

def recover_ecdsa(sig1, sig2, m1, m2):
    r1, s1 = sig1
    r2, s2 = sig2
    assert r1 == r2 # 因为k被重用
    e1, e2 = H(m1), H(m2)
    k = (e2 - e1) * pow(s2 - s1, -1, n)
    d = (s1 * k - e1) * pow(r, -1, n)
    return d

def recover_schnorr(P, sig1, sig2, m1, m2):
    r1, s1 = sig1
    r2, s2 = sig2
    assert r1 == r2 # 因为k被重用
    e1, e2 = H(r1 || P.x || m1), H(r2 || P.x || m2)
    d = pow(e2 - e1, -1, n) * (s2 - s1)
    return d

此外，如果对于同一个密钥生成的ECDSA和Schnorr签名使用了相同的随机数，还是能够恢复私钥，无论消息是否不同：

def recover_mixed(P, sig_ecdsa, sig_schnorr, m_ecdsa, m_schnorr):
    r_ecdsa, s_ecdsa = sig_ecdsa
    r_schnorr, s_schnorr = sig_schnorr
    assert r_ecdsa == r_schnorr # 因为k被重用
    r = r_ecdsa
    r_inv = pow(r, -1, n)
    e_ecdsa, e_schnorr = H(m_ecdsa), H(r_schnorr || P.x || m_schnorr)
    k = (s_schnorr + e_schnorr * e_ecdsa * r_inv) * pow(1 + e_schnorr * s_ecdsa * r_inv, -1, n)
    d = (k * s_ecdsa - e_ecdsa) * r_inv
    return d

Schnorr签名允许以聚合密钥的方式高效生成签名，仿佛它是一个独立的密钥，这是通过将部分签名求和生成的，部分签名者知道聚合公钥和个人私钥，而不需要一个单一的参与者持有组成聚合的私钥。如果(d1, d2)为私钥，则sig = sign_schnorr(d1+d2, m, k1+k2)是一个有效签名，公钥为(d1+d2)*G，根据verify_schnorr((d1+d2)*G, m, sig)。

这个过程可以通过一个持有d1和d2的参与者独立产生r值，即 r1 = k1*G, r2 = k2*G，相加产生r，将它们的公钥相加以产生聚合公钥(d1+d2)*G，计算共享的e = H(r || ((d1+d2)*G).x || m)，生成单独的s值s1 = k1 + e * d1和s2 = k2 + e*d2，然后将它们相加产生聚合签名的s = s1 + s2。像FROST这样的阈值签名方案详细说明了这个过程，包括确切的发送值、何时发送、如何处理多个签名者以及如何检测签名者提交不正确值的情况，因为如果中间值未经额外验证简单交换，一个参与者可能会使其他参与者的密钥被暴露。

生成聚合ECDSA签名的协议需要比生成聚合Schnorr签名的协议更多的轮次，详见 ECDSA阈值签名调查↗。

与BLS签名不同，Schnorr签名在创建时不能根据各个公钥聚合，因为如果(r1, s1) = sign_schnorr(d1, m, k1)和(r2, s2) = sign_schnorr(d2, m, k2)，用于计算s1和s2的中间值e1 = H(r1 || (d1*G).x || m)和e2 = H(r2 || (d2*G).x || m)包含了个别公钥的哈希，这在聚合公钥(d1+d2)*G中不会匹配。

脚本虚拟机

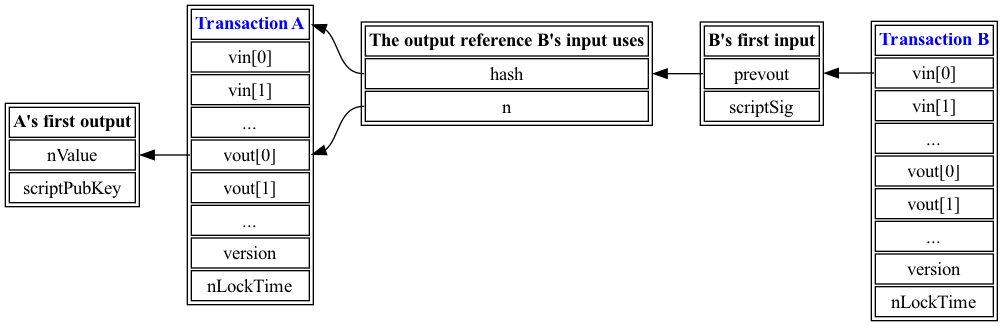
比特币脚本是基于栈的虚拟机程序，由在栈顶部及附近的数据操作的操作码组成。栈元素是可变大小的字节字符串，每个栈元素的最大限制为520字节。基于栈的程序可以通过连接它们进行组合，这使得第二个程序在栈数据的输入上操作由第一个程序生成的输出。

每个比特币交易输出包含一个名为scriptPubKey的脚本，它指定可以花费输出的条件。

后续交易输入为了花费先前交易的输出，提供一个名为scriptSig的脚本，该脚本提供输出的scriptPubKey的输入栈。为了使输入-输出对有效，连接的scriptSig和scriptPubKey的执行必须无错误地停止，并且栈顶的元素必须为非零。

简而言之：

• scriptPubKey是输出的一部分，是一串VM操作码，用于检查输出的花费条件是否得到满足。
• scriptSig是输入的一部分，它“解锁”scriptPubKey。它也是一串VM操作码，并且被加到scriptPubKey之前，组合后的字节代码在虚拟机中执行。

支付到公钥哈希

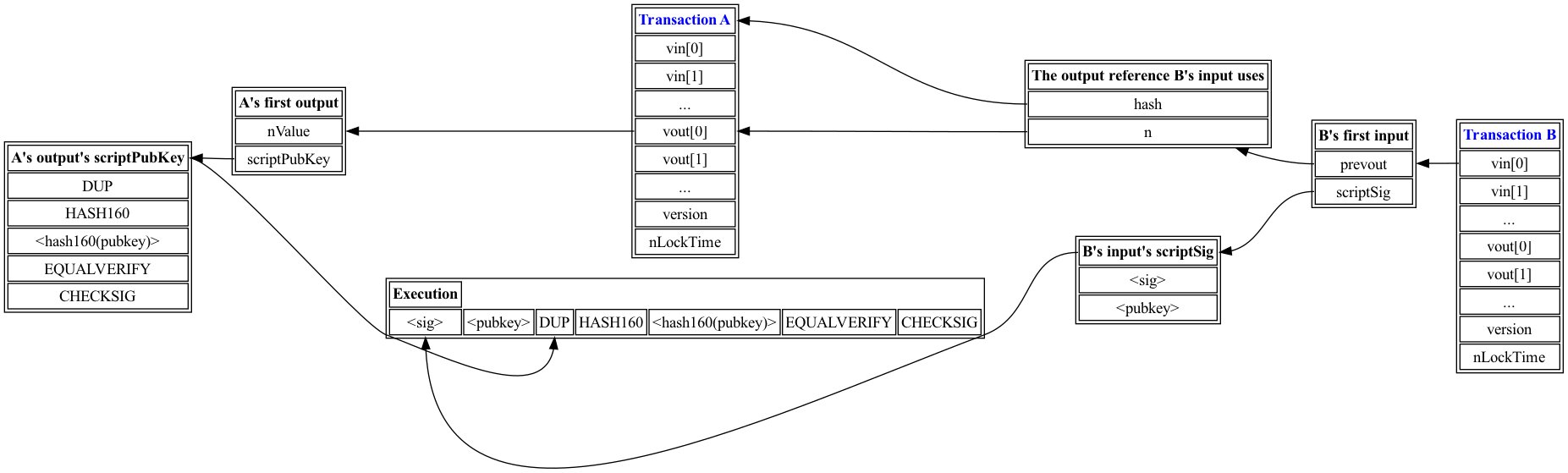
最常见的scriptPubKey脚本称为支付到公钥哈希（P2PKH），它通过要求整个交易必须由特定密钥对签名来使得输出可以被消费。

它由OP_DUP OP_HASH160 <hash160(pubkey)> OP_EQUALVERIFY OP_CHECKSIG组成，强制对应的scriptSig为<sig> <pubkey>的形式，其中<data>表示推送字面数据的指令。

在组合脚本中，<pubkey> OP_DUP OP_HASH160 <hash160(pubkey)> OP_EQUALVERIFY强制栈顶的元素是指定的哈希，将其留在栈上（由于OP_DUP），如果哈希不匹配或者栈元素不足则会中止（导致交易无效）。

在此之后，剩下的执行状态<sig> <pubkey> OP_CHECKSIG验证sig是否为整个交易的ECDSA签名（脚本的内容可以排除，以避免需要找到哈希函数的定点导致的循环）由pubkey签名。

支付到脚本哈希

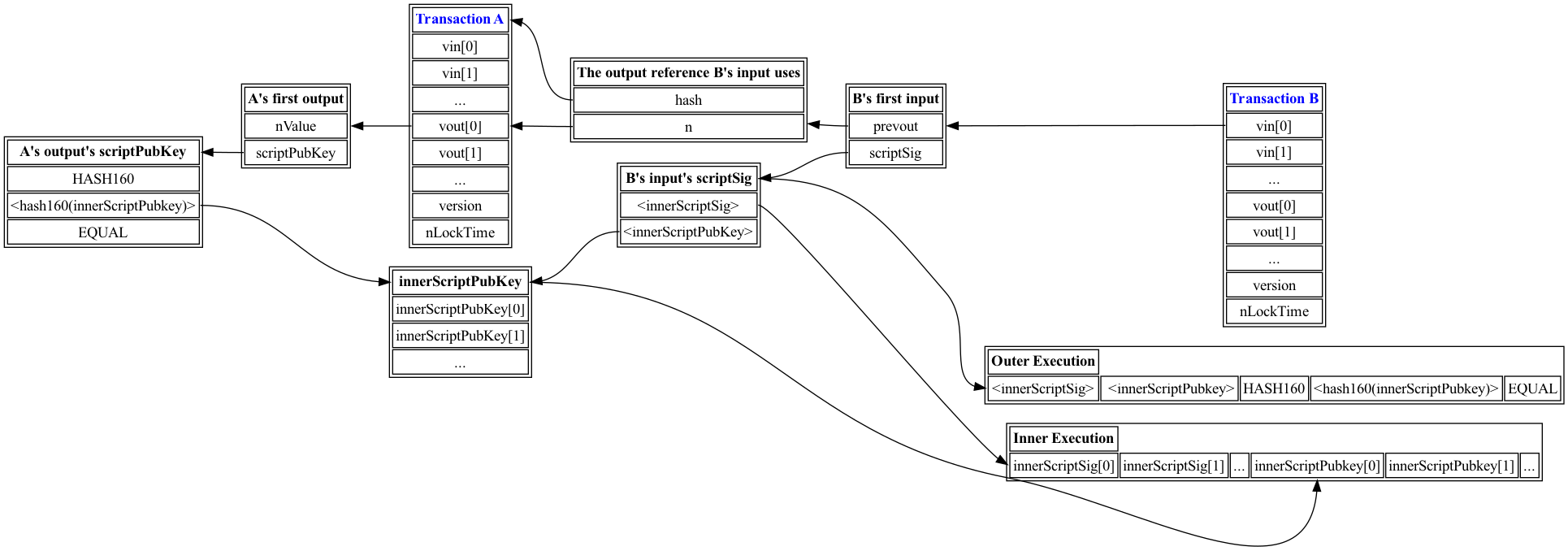
比特币改进提案BIP-16↗引入了能力，使得交易输出可以以固定大小的哈希指定其消费条件作为对该脚本的承诺，而不是直接包含可变大小的脚本，将存储脚本的开销推迟到消费该输出的交易。

它通过对消费scriptPubKey格式为OP_HASH160 <data-of-length-20> OP_EQUAL的输出进行额外验证，称为支付到脚本哈希（P2SH）交易来实现。在BIP-16以前，比特币的实现将此scriptPubKey按原样解释，只要求在执行组合输入scriptSig和输出scriptPubKey后，栈顶元素具有指定的哈希。

包含BIP-16的实现增加了额外的验证要求。它们将输出的scriptPubKey中的通过哈希得到的值（图中的innerScriptPubKey）视为序列化脚本。此序列化脚本作为一个新的scriptPubKey。在验证期间，外部执行将内部scriptSig推送到栈上。然后，此内部scriptSig将在脚本虚拟机的另一执行中针对新的scriptPubKey执行。此第二次脚本执行也必须成功，才能将交易视为有效。实质上，外部执行验证提供的脚本是否与输出中承诺的哈希匹配，而内部执行则实际运行该脚本中编码的消费条件，即“支付到脚本哈希”的“脚本”部分。

SegWit版本0

在BIP-141↗之前，SegWit脚本直接包含在区块中的交易内，要求它们被复制到任何处理区块的实体上，即使那些不验证脚本执行的实体。SegWit允许交易选择性存储其脚本于一个独立的见证树（witness tree）中，其根哈希作为主区块的一部分被承诺，并且在费用计算中，这些字节都被认为仅为主区块字节的三分之一。SegWit交易输出使用一个小的scriptPubKey，由指示在见证中期望的数据显示的元数据组成（在BIP-141采用之前，这一元数据会由于无法成为有效交易而被视为无效，确保只有采纳BIP-141的节点才认为消费SegWit交易输出有效）。该元数据包括一个版本字节，BIP-141仅定义版本0的消费规则，留下其他版本供未来提案以向前兼容的方式解释。消费SegWit输出的交易输入的scriptWitness字段不包含在常规区块中，但包含在见证区块中。一个见证区块可以通过哈希化交易输入的见证并检查其是否与对应常规区块中承诺的根哈希匹配来验证。

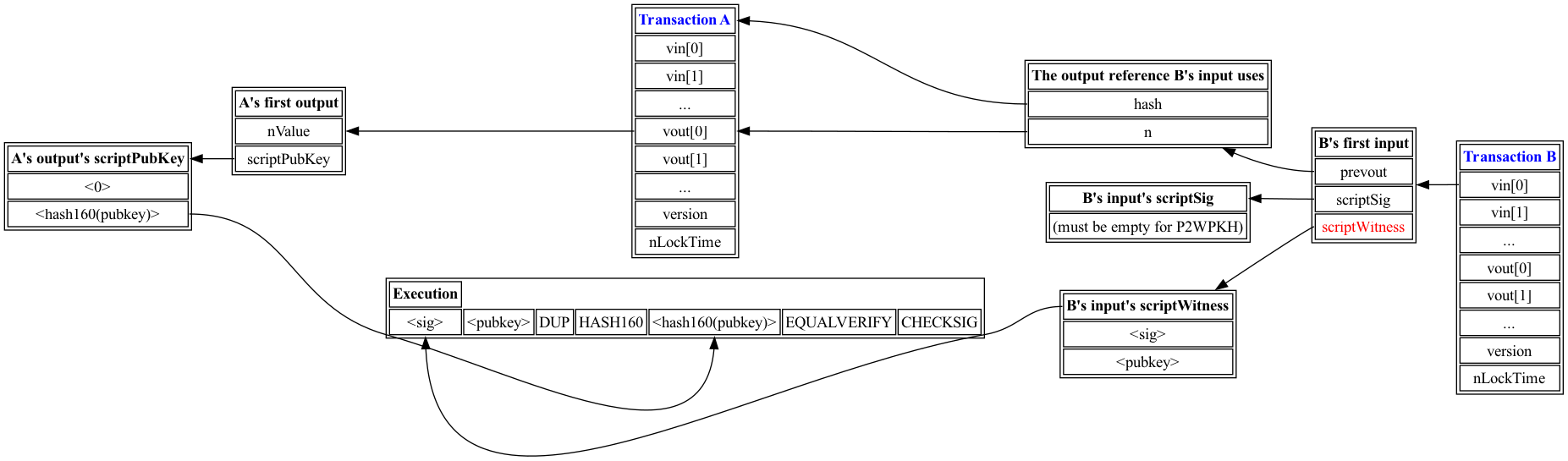
SegWit V0的scriptPubKey必须是支付到见证公钥哈希（P2WPH）或支付到见证脚本哈希（P2WSH）。P2WPH脚本是公钥的20字节HASH160哈希，要求见证脚本由一个签名和公钥组成，这些都会被验证就像通过P2PKH脚本一样。P2WPH脚本比P2PKH脚本短三字节，因为使用了SegWit版本字节，而不是P2PKH脚本中的四个操作码。P2WSH脚本是对要从见证脚本的最后一个元素反序列化的脚本的32字节SHA-256哈希，与脚本哈希进行验证，然后与见证脚本的其余部分连接。这使得可以与SegWit一起使用任意脚本，脚本的大小在区块中占用恒定数额的空间（而不是线性）。P2WSH与P2SH共享优点，直到输出被消费，脚本才会被揭示，并且它通过将脚本的透露从区块移动到见证来另外节省费用。

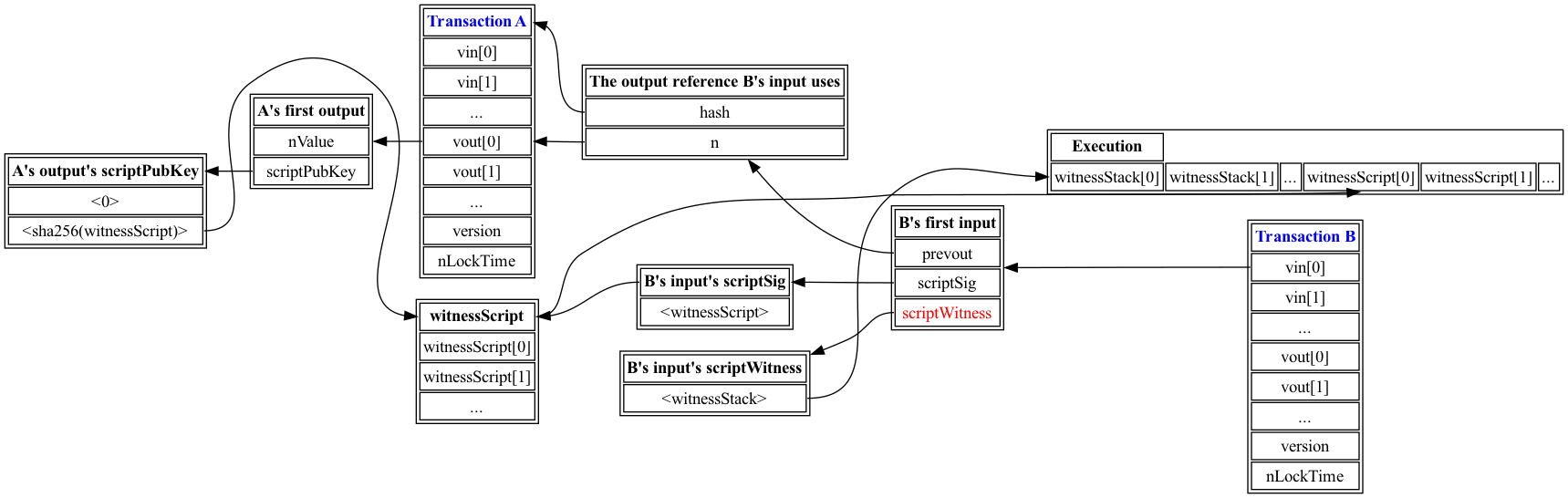
Taproot脚本

BIP-341↗的Taproot定义了版本1的SegWit交易输出，以包含点Q = P + H(P || m)*G，并可以通过提供Schnorr签名与Q为公钥的交易数据或提供P、脚本s以及证明s包含在Merkle根m中来赎回。（包含证明用于计算m，然后用于重新计算Q并检查它是否与SegWit元数据中的Q匹配）。与P2WSH类似，脚本在作为一个见证输入出现在消费它们的交易中之前并不揭示。

如果签名者知道内部密钥P（即，标量d使得P = d*G）对应的私钥，他们也会知道输出密钥Q所对应的私钥，因为Q = P + H(P || m)*G = d*G + H(P || m)*G = (d + H(P || m)*G)。

Taproot有几个特殊情况具有重要意义：

• 如果m是对一个空Merkle树的承诺，这提供了一种Schnorr变体的支付到公钥方式，这使得通过密钥聚合实现更便宜的多重签名交易。这种用法类似于P2PKH。

• 如果P构造得使得相对于G没有已知离散对数，则提供了一种P2SH变体，它支付给一组脚本的逻辑或，但仅执行的脚本会使见证空间耗费。

• P键可以以确定性的方式构造，使得没有已知离散对数，即，P = H = lift_x(sha256("\\x04"||G.x||G.y))（其中lift_x生成具有指定x坐标和偶数y坐标的曲线上的唯一点），这允许任何人验证一个Taproot输出是对特定脚本集合的承诺，前提是他们知道这些脚本。

• P键可以以非确定性的方式构造，P = H + rG，其中r是随机的，这使得Taproot输出与带有任意公钥的一个输出无法分辨，但允许通过向验证者揭示r（或通过提供一个零知识证明，证明存在这样的r使得P被正确计算）来证明输出创建者并不知晓P的离散对数。

此外，具有在比特币脚本中可验证的边际条件的状态机可以通过使用既消耗也生成Taproot输出的交易来表示（尽管需要契约约束输出来限制输出）。BitVM和Babylon都以这种方式编码状态机，前者编码执行电路的欺诈证明的状态机，后者编码作为权益的比特币的绑定和解绑状态机。

契约和契约模拟委员会

交易输出的脚本目前无法依赖于支出的交易的任意字段。如果一个脚本能够依赖于支出其输出的交易的输出，它可能要求该输出的脚本具有特定值。将这些约束链式连接到固定深度可以编码状态机：输出A可能要求支出它的交易的一条输出是脚本B并有某个最低值，而C可以在下一个交易中输出。

使用OP_CAT操作码的通用契约（其连接两个栈元素）在BIP-347↗中被提议重新启用，OP_CHECKSIGFROMSTACK操作码（它将检查任意数据的Schnorr签名，在BIP-348↗中指定）也被提议。它们将允许脚本依赖于任何字段，前提是这个字段包含在交易哈希中，通过单独包含交易字段（根据需要进行复制以执行额外检查），将它们用OP_CAT连接，计算交易哈希并检查其是否具有有效的签名（使用OP_CHECKSIGFROMSTACK），并且检查签名在交易本身也是有效的（使用OP_CHECKSIG），这确保在scriptSig中提供的字段实际上是交易构成的字段。

带有OP_CHECKTEMPLATEVERIFY操作码的模板契约（在BIP-119↗中指定）允许依赖于交易字段的特定子集，它们旨在使创建自我传播的契约不可行（其中脚本A要求A的副本出现在下一个输出的脚本中），这种情况是可能通过同时使用OP_CAT和OP_CHECKSIGFROMSTACK的契约。

由于这些操作码目前在比特币脚本中不可用，按照契约的协议通常使用契约模拟委员会，该委员会签署满足契约将强制的限制的交易。在交易的脚本将强制实施契约的地方，它们转而检查该协议的契约模拟委员会的某个阈值是否已签署交易。对于强制执行状态机的交易集，契约模拟委员会可以一次性签署整个交易集。由于这些交易要求额外的签名提交给比特币（例如，要求提交初始交易的用户提供资金的签名或根据他们想采取的行动要求其他方签名），契约模拟委员会无法提前提交其共同签署的交易，并且用户可以选择避免进入状态机，前提是该委员会仅签署它们的一部分。

FROST签名

灵活的轮次优化Schnorr阈值签名↗（简称FROST签名）是一种协议，用于由n个参与者共同生成一个标准的Schnorr公钥，以便其中的任何t个可产生相应消息的签名（即t-of-n阈值签名）。与直接使用Shamir密钥共享不同，对应的私钥在签名操作期间不会被显式恢复。

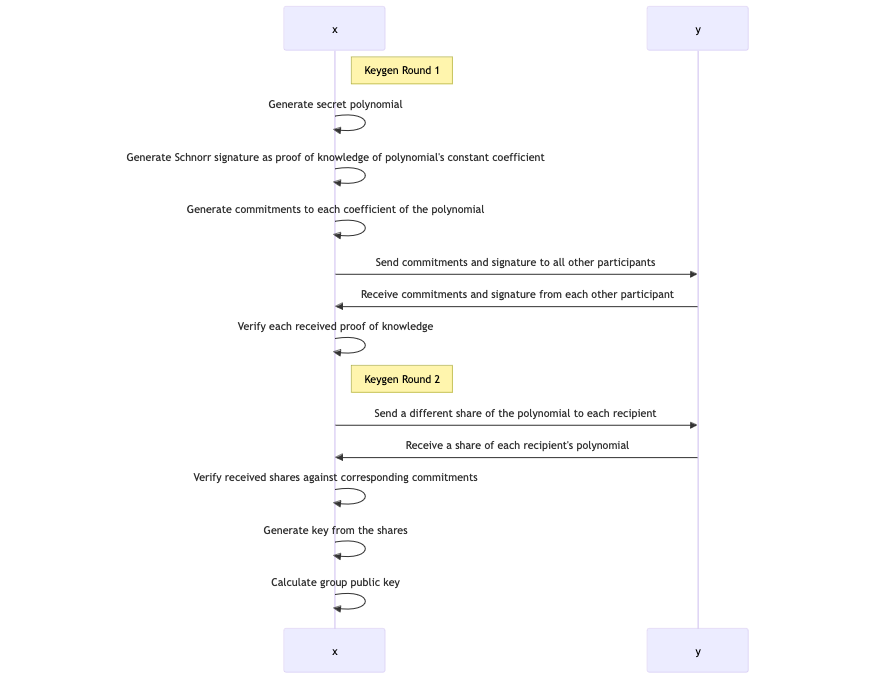
FROST分布式密钥生成需要两个轮次，并生成一个可以与相同签名者集签署消息的长期密钥。在这个过程中，每个参与者生成随机的度为t - 1的多项式，利用离散对数承诺方案对系数进行承诺，通过生成包含参与者索引和使用常数系数的步骤的消息的Schnorr签名来生成对常数系数的知识证明，广播这些承诺和证明（使每个参与者都可以验证其他参与者在消息间使用其多项式是否一致），并向每个参与者发送其多项式的部分密钥的加密分享。每个参与者作为接收者验证每个发送者的知识证明和分享与发送者的承诺是否一致，如果没有不一致，便插值生成该接收者的签名密钥的分享。如果发送者偏离了协议，发送互不一致的分享，则会被检测到，可以重新启动密钥生成，将该发送者排除在外。

FROST签名可以通过两轮进行（如果一次只签署一条消息）或一轮（如果预先计算了一批随机数）。随机数使用加法分享生成（并通过承诺防止个别恶意参与者抵销所看到的随机分享之和），然后转化为Shamir分享，结合长期的签名分享计算签名。

除了上述论文外，非批量签名协议还在IETF\ RFC-9591↗中进行了说明。

frost_secp256k1_tr↗ crate是一个FROST实现，生成与BIP-340兼容的签名，它被zkBitcoin↗和Nomic↗使用。Penumbra有一个decaf377-frost↗实现，它与frost-core实现共享frost-secp256k1-tr实现，但使用decaf377椭圆曲线而不是Secp256k1。

项目预览

现在我们将看看一些项目是如何在自己的软件中使用这些元素的。

BitVM

BitVM↗利用Taproot脚本允许两个参与者（一个证明者和一个验证者）承诺于一个电路，创建一个可被输出电路结果确定的参与者消费的UTXO，如果证明者提供用于评估电路的输入，或者如果证明者对电路评估不正确或未提供输入，则可以被验证者消费。直接在比特币脚本中执行电路会导致脚本大小与电路门数成线性增长，对于更大的电路来说是不可行的。BitVM的最好情况是一条交易，在成功路径上的2-of-2多重签名，其中证明者和验证者同意在链外执行电路。备用方案是一个交互式欺诈证明，其时间与电路的深度成比例（通常为电路门数的对数），在此情况下，对于电路执行错误的任一方将其押金损失给予正确的一方。

为了证明这一点具有普适性，仅需将布尔电路编译为比特承诺和NAND门，但为了效率，这也可以与算术电路一起完成。

对于电路中的每一位，证明者创建对应的比特承诺脚本片段w_0和w_1，以及OP_IF OP_HASH_160 <H(w_0)> OP_EQUALVERIFY <0> OP_ELSE OP_HASH_160 <H(w_1)> OP_EQUALVERIFY <1> OP_ENDIF。如果发布了w_i，这个脚本可以通过<w_i> <i>满足，从而承诺脚本成功，推送值<i>到栈。知道任一预影的人都无法满足该比特承诺脚本。证明者可以通过将预影发送给验证者来设置链外电路的输入。

电路的每个NAND门可以被编码为一个脚本，该脚本使用输入的预影a_i和b_j以及输出的预影c_k，使用用于比特a和b的比特承诺脚本，将i和j推送到栈中以计算i NAND j，使用用于c的比特承诺脚本将k推送到栈中，并验证k = i NAND j。对于电路中的每个门，以及对于每轮欺诈证明协议，验证者构造一个请求的哈希锁，以请求证明者评估该门，通过选择一个在执行该门之前所需哈希的预影。

在欺诈证明过程中，从验证者开始，证明者和验证者轮流提交出一次进展BitVM状态机的交易（它们预签名，就像它们是契约模拟委员会一样，因为没有契约）。需要某一方进行的边缘在该边缘的叶子脚本中都有检查该方签名的条件。内部Taproot键是由证明者和验证者持有的密钥聚合构成，允许2-of-2多重签名用于快速成功路径。每个状态还具有一个时间锁路径，任一方都使得对方的行动无法无限制延迟，使其无法损失。

为了确保证明者以一致的方式评估电路（例如，在一个方程中以c_0为输出而在不同的方程中以c_1为输入，或在线上和线下承诺不同的输入），在验证者的回合中，如果他们同时获得同一门的两个预影，验证者会立即声 claim 押金（实现方式是，对于每个门，添加一个Taproot叶子脚本，要求该门的两个预影）。

在验证者的回合，他们可以通过发布相应哈希锁的预影，来选择证明者下一个评估哪个门。证明者随后必须提供所选门的输入和输出的预影（通过执行对应于该哈希锁和门方程的叶子脚本）。

由于通过调用欺诈证明，一个诚实的验证者与证明者在电路输出上的意见不一致，他们请求的第一个电路评估门将是电路整体输出的最后一个门。通过为电路的最后一个门提供输入，证明者揭示了其输入的子树与验证者输入所在子树不一致（因为验证者可以从他们的链外输入向前计算）。按照自底向上的方式，验证者可以在电路的深度内达到其输入，在这个点上，他们拥有来自链外提供的输入预影，而此预影与证明者在链上的输入预影不一致，使其能够主张押金，因为他们知道该输入的两个预影。

如果验证者无法在指定的轮次内证明证明者所选输入的不一致，证明者就以与他们给验证者的输入一致的方式评估电路，并得到押金。

请注意，与恶意电路或零知识证明相比，任一方的输入都是公开的。证明者的输入直接在链上和验证者可见，如果验证者以类似于链外转移的方式获得其输入承诺，通过与证明者进行无知转移以获取与他们的输入比特相应的承诺，而不向证明者透露这些比特，验证者就能够发起虚假的欺诈证明，因为证明者不知道如何对于验证者的输入评估电路。然而，电路本身可以作为内部零知识证明算法的验证，这由BitVM Bridge↗完成。

BitVM2

BitVM2↗提供了一种与BitVM类似的原语，增强了其灵活性和效率。它的程序表示与BitVM不同，证明者对一个随机长度的比特币脚本进行承诺（这些脚本拆分为每个个体不超过本地执行比特币脚本支持的最大重要部分），而不是布尔电路。这种表示形式允许更高效的欺诈证明，所需轮次为固定轮次，与块数无关（而对应BitVM的电路门数为对数轮次）。BitVM2的欺诈证明比BitVM更灵活，允许任何比特币用户在证明者声称程序的不一致执行时参与验证者角色，而不需要为每对证明者和验证者进行准备。

对于每个协议实例，证明者为程序的每个块创建一个Lamport密钥对。Lamport密钥对的统计方式是使用固定长度比特字符串的比特承诺，这比在BitVM中使用的要广泛。与BitVM不同，Lamport签名并不被间接用于欺诈证明（如果同时签署了多个消息则揭示部分密钥；请注意，对于1比特的Lamport签名，密钥等于签名），而是作为一个在比特币脚本中可验证的数据的签名方案（OP_CHECKSIG仅支持在交易上检查签名，而OP_CHECKSIGFROMSTACK ↗，这会支持这一点，但不在比特币中）。证明者使用这些签署在执行每个块后得到的堆栈，这样如果他们对于整个程序宣称获取的输出不正确，验证者就可以逐块状况地执行程序，找到执行结果与输入不一致的第一个块，此时他们拥有一个可以与链上的执行与段结果进行不一致验证的输入输出对的签名。

BitVM2协议使用了契约模拟委员会，这是一组签名者，确保证明者的交易与协议所要求的结构匹配，通过n-of-n多重签名签署这些交易。

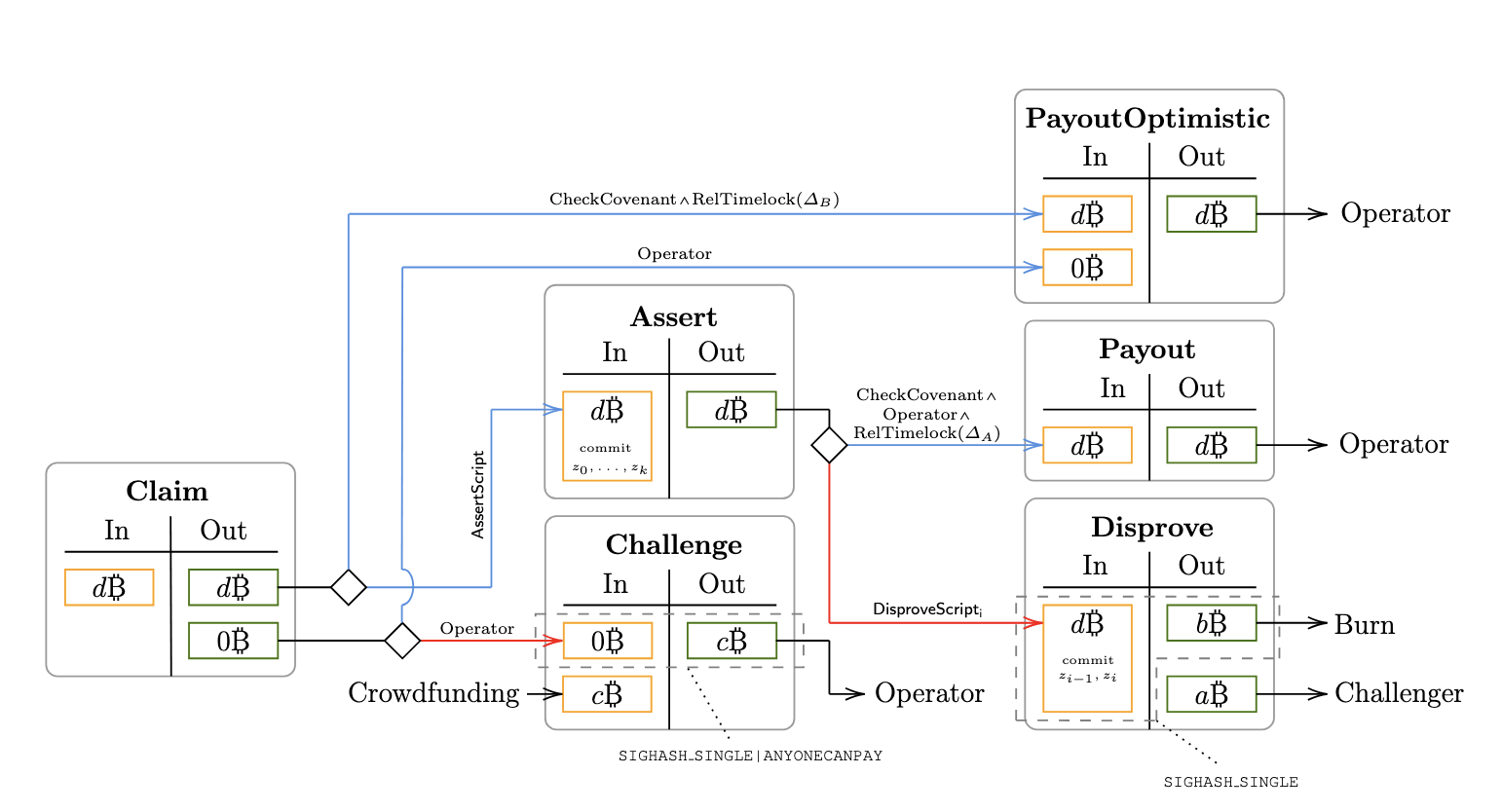为了承诺执行程序，证明者创建了一组六个链接的交易，使证明者能够在稍后对输入评估程序，然后在时间锁到期后，如果其输出对该输入是正确的，则收到押金；否则，对于任何注意到声称输出不正确的验证者，可以提交欺诈证明并代替收到押金。

这些交易如下所示：

• Claim 交易接收一个资金输入（这允许证明者以外的人为此协议提供资金）并指定要验证的程序的初始堆栈值。其第一个输出是一个带有时间锁的 Taproot 输出，用于 PayoutOptimistic 路径和 Assert 路径，该路径检查 Lamport 签名以承诺到链上的声明中间状态。其第二个输出是一个零值连接输出，用于 PayoutOptimistic 和 Challenge 交易以确保它们互斥。
• PayoutOptimistic 交易的输入是 Claim 交易的 Taproot 输出的时间锁路径以及其连接输出，其输出可由证明者支出。这用于避免在时间锁期内没有挑战时将对中间状态的承诺发布到链上。
• Challenge 交易将 Claim 交易的连接输入和验证者支付作为费用的资金输入作为输入。其输出可由证明者支出。此费用劝阻验证者提出虚假的挑战，并覆盖证明者发布 Assert 交易的交易费用。
• Assert 交易使用带有 Assert 路径的 Claim 交易输出，该路径在链上承诺中间堆栈值和 Lamport 密钥。其 Taproot 输出包含用于挑战每个要验证的程序块的叶子（每个都检查提供的输入和输出签名，执行该块，并检查输出与签署的输出是否匹配）以及一个成功路径叶子，使证明者在时间锁后能够使用他们的公钥支出输出。
• 用于块的 Disprove 交易将 Assert 交易的 Taproot 输出作为其输入，执行显示该块执行不正确的叶子。它有两个输出，其中一个必须使指定金额的押金不可支出；另一个允许验证者支出其余部分。
• Payout 交易将 Assert 交易的 Taproot 输出作为输入，执行时间锁路径，使证明者能够支出押金。

BitVM Bridge 利用 BitVM2 实现将 BTC 桥接到其他区块链。它要求对方区块链具有比特币轻客户端，并且对方区块链将其状态发布到比特币。用户通过向比特币网络提交验证方识别的交易将 BTC 发送到对方区块链，在对方区块链上铸造桥接的 BTC。对方区块链上的用户可以通过燃烧桥接的 BTC 并生成 Groth16 证明，证明桥接的 BTC 已被燃烧，将其发送回比特币，该证明由比特币上的 BitVM2 实例进行验证。

zkBitcoin

zkBitcoin↗ 允许创建以零知识电路给定支出条件的比特币输出，称为 zkApps。

与 BitVM 不同，它并不直接在链上验证证明；它拥有一个 FROST 参与者委员会，该委员会管理一个阈值签名钱包，验证发送给它的零知识证明，并签署相应的交易。

该实现使用 PLONK 作为证明系统，该系统具有通用设置，允许委员会对多个电路使用相同的设置。zkApps 的创建者将其指定为 Circom 程序，而 zkBitcoin 的工具将其部署到比特币网络。

无状态 zkApps 由两个输出的比特币交易创建，这两个输出被 zkBitcoin 委员会识别：一个将要由 zkApp 管理的值发送到委员会地址，另一个通过将其作为 OP_RETURN 的直接参数包括来承诺一个电路的验证密钥的哈希（后一个输出是不可支出的）。委员会签署以 zkApp 输出为输入并包含费用的交易，如果其提交者提供的验证密钥与 zkApp 的验证密钥哈希匹配，并且一个与该验证密钥和交易哈希作为公共输入一起验证的证明。这允许电路通过从私有输入中推导出交易哈希并将其约束为公共输入，强制交易结构的附加约束。

有状态 zkApps 类似，并且在创建它们的交易中额外包括带有验证密钥的初始状态。除了交易哈希，公共输入包括旧状态和新状态以及提款和存款金额。这允许电路根据旧状态强制计算新状态，并对提款和存款金额施加状态依赖条件。委员会在电路外强制提款和存款金额、有状态 zkApp 的余额，以及交易输入和输出的余额。

zkBitcoin 钱包从比特币的角度来看是一个普通的钱包；它可以支出的输出是没有脚本路径的 Taproot 输出，以支持与 FROST 一起使用 BIP-340 Schnorr 签名。因此，zkBitcoin 的安全性依赖于委员会成员没有在协议之外聚合其密钥材料，无论是通过协作还是黑客攻击，从而重构出可以在没有约束的情况下支出 zkBitcoin 钱包资金的私钥。

Babylon

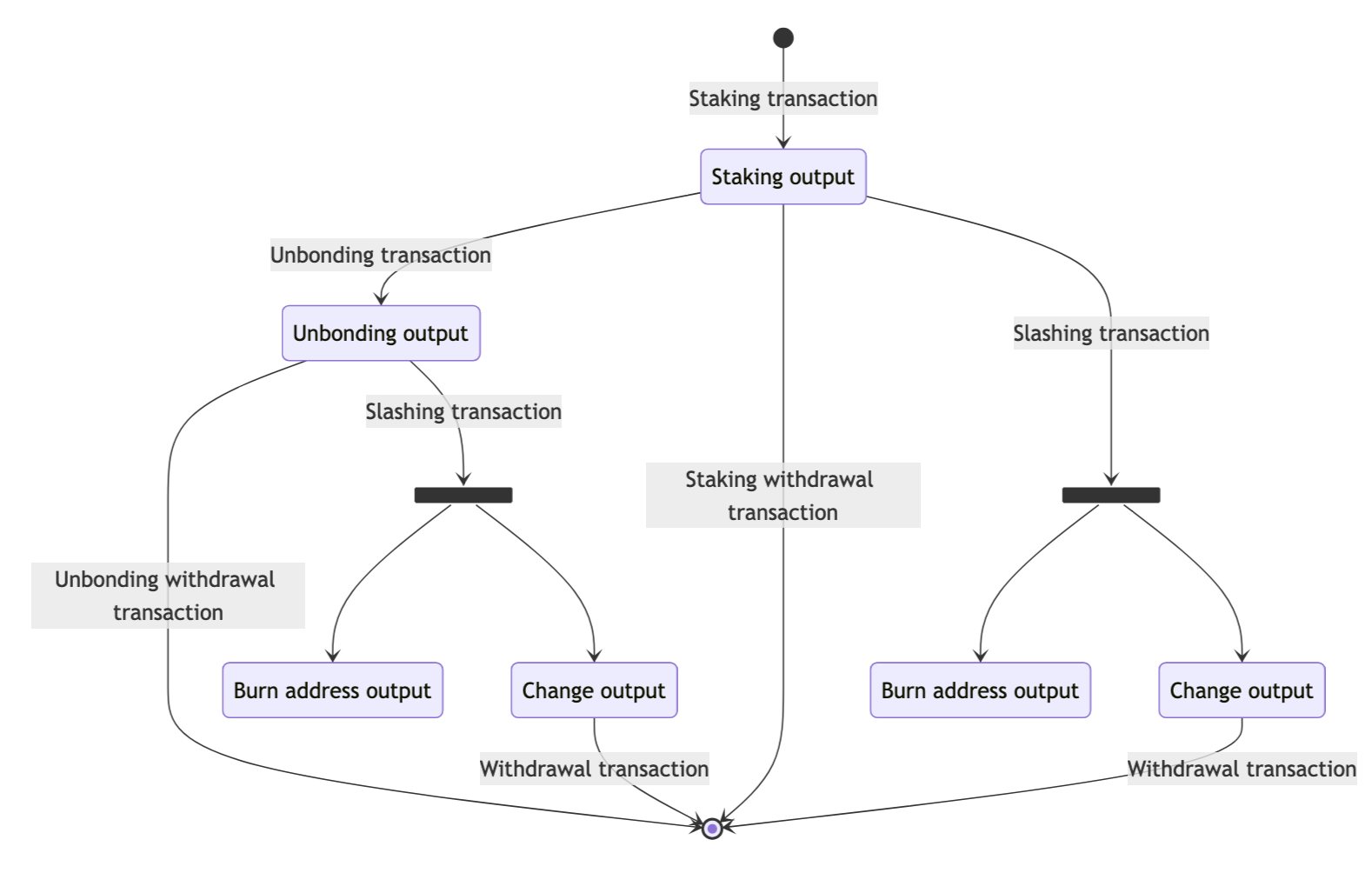
Babylon↗ 是一个由比特币质押保证安全的权益证明链。质押者委托给终结提供者，后者在 Babylon 链上签署区块以提供共识。终结提供者在共识中的投票权重与委托给他们的 BTC 成比例，质押者根据其质押金额按比例获得 BBN。如果终结提供者尝试通过为同一高度签署两个不同的区块进行双重消费，他们的委托人将被削减：10% 的委托金将发送到一个不可支出的燃烧地址，剩余的 90% 将退还给质押者。在没有恶意终结提供者行为的情况下，质押者可以在 101 个比特币块（大约 17 小时）内解锁以接收其质押的 BTC，在此延迟期间仍然可以发生削减。

Babylon 使用 Taproot 脚本确保质押资金仅根据此状态机可用。质押交易包含对质押输出的承诺，一个由三个脚本组成的 Taproot 输出，带有一个确定性的不可支出的内部密钥，允许通过从委托数据重建质押交易来识别。

质押输出的第一个脚本是时间锁路径，它要求质押者的签名和一个基于没有解除质押时委托意图持续时间的 BIP-112↗ OP_CHECKSEQUENCEVERIFY 时间锁。第二个脚本是解除质押路径，要求质押者的签名和 Covenant Emulation Committee 成员签名的阈值，强制执行解除质押交易的结构。第三个脚本是削减脚本，要求质押者的签名；一组 Covenant Emulation Committee 成员签名的阈值，这些成员强制执行削减交易的结构；以及被委托的终结提供者的签名，其密钥通过用于签署区块的签名结构显露，如果为同一高度签署多个区块。

解除质押交易由 Covenant Emulation Committee 预签名，通过第二条路径消耗质押输出，并具有具有两个路径的解除质押输出：一个时间锁路径，要求质押者的签名以及 101 块 OP_CHECKSEQUENCEVERIFY 时间锁，以及一个具有与质押输出的削减路径相同要求的削减路径。质押脚本的解除质押路径要求 Covenant Emulation Committee 成员的签名，以确保仅在此延迟期间执行。

削减交易（各一个针对质押和解除质押输出）必须由质押者签署，以使其委托生效。Covenant Emulation Committee 强制削减交易燃烧委托的 10% 的股份。终结提供者使用可提取的一次性签名签署权益证明区块——这是一种 Schnorr 签名变体，它根据正在签署的区块的高度将随机数 k 作为函数推导键——终结提供者的密钥，将 R 值提交到 Babylon 链，然后再提交 s 值（类似于离散日志合约所称的提交 R 点签名）。这确保如果他们尝试为同一高度提交两个不同的 s 值，有足够的信息可以通过 recover_schnorr 恢复终结提供者的密钥，允许任何观察到双重签名尝试的人将削减交易提交到比特币网络。如果终结提供者诚实地签署，每个高度最多一个区块，他们正在使用不可预测的随机数，这不会泄露他们的私钥。

离散日志合约

离散日志合约↗ 提供了一种机制，允许 oracle 以一种方式发布区块链外的数据（例如，价格数据），使一对当事方可以预签署交易，其中一项可以基于公开价格进行支出（例如，基于价格数据效力的外汇换算），而无需 oracle 从当事方接收任何输入（甚至无法检测其输出是否被特定交易使用）。

oracle 使用承诺的 R 点签名，这是一种变化 Schnorr 签名，其中随机数 k 被采样，R = kG 在消息或签名的 s 值已知之前发布。对于价格数据，oracle 对每个资产和每个时间窗口承诺一个不同的 R 点。当要公布价格数据条目时，oracle 将价格作为消息签名，并与其时间窗口相关的 R 点一起签名。

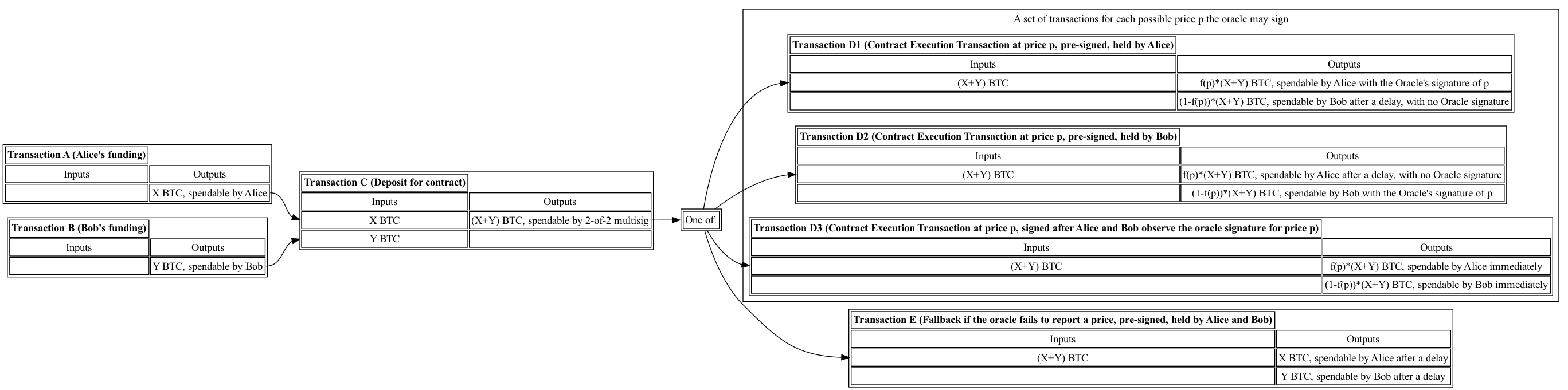
要根据来自价格数据的未来价格执行兑换，两方资助一个多重签名输出，并为每个消费该输出的可能消息预签署一笔交易。这些交易具有基于消息的值的输出，其中一个输出直接发送到对方作为 P2PKH 输出，另外一个具有支出条件（论文中的 P2SH，但 P2WSH/Taproot 也可工作），允许其中一方使用更改过的公钥立即支出，该公钥包含与相应消息有关的 sG（可从 oracle 的公钥、R 和消息计算得出），或者在时间锁后由对方支出。

oracle 对于一条消息的签名 s 允许持有公钥 A = aG 的方支出 P2SH 输出，要求 pubkey A+sG，因为他们知道对应的私钥 a+s，允许他们立即从 P2SH 输出中索回其在兑换中的输出，而他们的对手则可以索回 P2PKH 输出。如果一方为错误消息发布交易，使用公钥 A+s1G（消耗多重签名输出），时间锁路径允许对方索回 P2SH 输出，因为第一方不会知道 s1，因为 oracle 将会发布一个独特的签名 s2。

如果 oracle 对同一 R 签署多个消息（例如，同一时段的多个价格），他们将通过随机数重用泄露其长期私钥。为了解决 oracle 无法提供任何输出的情况，双方可以预签署一笔交易，允许两人从多重签名输出中获得退款，并加入时间锁。为了解决 oracle 在未经签署多条消息的情况下错误报告价格的情况，可以使用多 oracle 的结合，其中交易在所有 oracle 同意的情况下有效，并使用时间锁退款路径来处理不匹配。

关于我们

Zellic 专注于保护新兴技术。我们的安全研究人员在最有价值的目标中发现了漏洞，从财富 500 强到 DeFi 巨头。

开发者、创始人和投资者信任我们的安全评估，以快速、自信且无重大漏洞地发布。凭借我们在现实世界的攻击安全研究的背景，我们能够发现他人所忽略的。

联系我们↗ 进行优于其他审核的审计。真正的审计，而不是走过场。

• 原文链接： zellic.io/blog/building-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～