关于 rStar-Math：展示如何通过深度思维使小型语言模型超越大型模型

简要概述：本文讨论了引入rStar-Math的论文以及小型语言模型在数学相关任务上超过更复杂的大型语言模型的技术。你可以在这里查看代码。rStar-Math显著提高了SLM的数学推理能力。例如，在MATH基准测试中，它将Qwen2.5-Math-7B的性能从58.8%提升至90.0%，Phi3-mini-3.8B的性能从41.4%提升至86.4%，超越了OpenAI的o1-preview模型。此外，在美国数学奥林匹克(AIME)中，rStar-Math解决了平均53.3%的问题，排名在高中数学学生的前20%。

引言

大型语言模型（LLMs）是高级人工智能系统，旨在理解、生成和处理人类语言。它们在包含数十亿单词的庞大数据集上进行训练，使它们能够执行各种与语言相关的任务。

LLMs的主要特征：

• 规模： LLM包含的参数从数百万到数十亿不等，使其能够捕捉语言中的复杂模式和细微差别。
• 训练数据： 这些模型在多样的广泛文本语料库上训练，包括书籍、文章、网站和其他文本来源，从而使它们对不同背景下的语言使用有广泛的理解。
• 能力： LLM可以执行各种任务，如文本生成、翻译、摘要、问答等，通常具有类人水平的能力。

基础架构：

大多数LLM基于2017年引入的Transformer架构。该架构使用自注意力有效处理和生成语言，使模型能够考虑句子中单词的上下文，并捕捉长距离依赖关系。变换器的一大优势是学习迁移非常有效。因此，我们可以使用大量数据训练一个模型，然后使用微调训练另一个任务。能够适应多种任务的模型被称为基础模型。要处理数据，它必须首先转换为一系列Token。

大多数最先进的LLM使用变换器的解码器部分，叠加多次（例如24、48、72、100等）。每个解码器包含以下元素：

• 掩码自注意力：一个具有因果掩码的多头注意力子层，以确保Token无法关注未来的位置（我们会很快解释这些术语）。
• 前馈网络：一个具有非线性的逐位置双层MLP（多层感知机）。
• 残差连接和层归一化围绕每个子层。

解码器层m的最小示意图为：

MHA表示多头注意力函数，LayerNormalization是归一化函数，FFN是前馈神经网络。

注意力通过关联三个元素：键、查询和值，这些元素来自层输入的适当变换。这些变换是线性的，矩阵的元素应由模型学习：

$$ Q = H^{m−1}W_Q \

K = H^{m−1}W_K\

V = H^{m−1}W_V $$

注意力机制通过比较键和值以找到最佳匹配。确定两个向量之间相关性的一个方法是通过查询和键所形成角度的余弦，

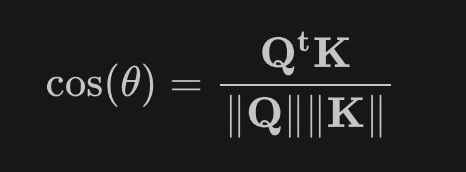
两个向量之间的标量积显示它们的相关性。在LLMs中，我们使用softmax函数，这确保激活将为正且最多为1：

$$ anm = exp(xtnxm) / ∑exp(xtnxl) $$

对注意力机制有两个必要的调整：缩放和因果性。第一个调整是为了重新缩放softmax函数的参数，以避免得到微乎其微的梯度。因果性确保一个Token无法关注未来的Token，以便模型只能使用当前或之前的Token，从而实现自回归生成。因此，

$$ Hatt,s = attention(Q,K,V) = softmax(QKt / √dk + M)V $$

其中M是掩码，使所有Token不应关注未来Token的位置等于−∞（以便当我们应用softmax函数时，这些元素等于零）。dk是键向量的长度。

多头注意力函数有h个不同的头（每个头都有自己的键、查询和值矩阵）。它将每个头的结果拼接起来（基本上是将它们一个接一个粘在一起）并应用一个矩阵Wo，

$$ headi = attention(Hm−1Qi, Hm−1Ki, Hm−1Vi)

Hatt = concatenate(head1, head2,…, headh)Wo $$

在注意力和归一化之后，每个Token的表示会经过一个逐位置的MLP（在每个序列位置独立应用，因此称为“逐位置”）：

$$ z = h, W1 + b1, z′ = σ(z), h′ = z′, W2 + b2, $$

其中：

• h∈ℝ^d是来自注意力子层的单个Token表示。
• W1∈ℝ^(d×dff), W2∈ℝ^(dff×d)。
• σ通常是GELU（高斯误差线性单元）或ReLU（ 修正线性单元）非线性（激活函数）。
• 这对于每个位置独立进行，因此在矩阵形式中：

$$ FFN(H);=;max $$

在读取文本或图像之前，它们必须先转换为Token。令输入为一系列Token：

$$ (x_1, x_2, \dots, x_T), $$

其中每个x_i是词汇表中的整数索引。我们将每个x_i映射到一个d维嵌入向量：

$$ \mathbf{E}(x_i) \in \mathbb{R}^d. $$

因此，输入序列被转换为一个嵌入矩阵：

$$ \mathbf{X} ;=; \bigl[\ \mathbf{E}(x_1);, \mathbf{E}(x_2);, \ldots; ,\mathbf{E}(x_T)\bigr] ;\in; \mathbb{R}^{T \times d}. $$

仅解码器的变换器仍然必须编码序列位置的概念。常见的方法包括：

• 学习的位置信息嵌入：为每个位置i提供一个可训练的\mathbf{P}(i) \in \mathbb{R}^d。
• 正弦（原始的变换器）：

$$ \begin{aligned} \text{PE}(i, 2k) &= \sin\Bigl(\tfrac{i}{10000^{2k/d}}\Bigr),\quad \text{PE}(i, 2k+1) = \cos\Bigl(\tfrac{i}{10000^{2k/d}}\Bigr). \end{aligned} $$

• 旋转位置嵌入（RoPE）：在查询/键空间中进行旋转（常用于GPT-NeoX、LLaMa等）。

无论哪种方式，下一步通常是：

$$ \mathbf{H}^{(0)} = \mathbf{X} ;+; \mathbf{P}, $$

其中\mathbf{P}表示位置信息（形状为\mathbb{R}^{T \times d}，与\mathbf{X}相同）。

应用：

• 自然语言处理（NLP）： LLM增强了各种NLP任务，包括情感分析、实体识别和语言翻译。
• 内容创作： 它们协助生成文章、报告，甚至创意写作，帮助作者和内容创作者。
• 客户服务： LLM驱动了聊天机器人和虚拟助手，在客户支持场景中提供类人交互。

挑战与考虑：

尽管其能力令人印象深刻，但LLM面临诸如以下挑战：

• 资源密集型： 训练和部署LLM需要大量计算资源，使得这些资源主要供大型组织使用。
• 伦理关注： 出现偏见或不当内容的生成以及潜在的滥用问题，要求谨慎考虑和负责任的部署。
• 可解释性： 理解LLM的决策过程可能很复杂，这引发了关于透明度和可信度的担忧。

一般来说，考虑到参数集更大的情况，期望LLM的响应质量和能力更高。该方法的问题在于，模型的训练和微调成本变得高不可攀，并且无法由用户在本地运行。论文展示了如何通过深度思考和使用以下概念和想法，使小型LLM优于更强大的LLM：

• 代码增强的思维链（CoT）数据合成：此方法通过执行广泛的蒙特卡罗树搜索（MCTS）回放生成逐步验证的推理轨迹。这些轨迹用于训练政策小型语言模型（SLM），确保其学习准确且逻辑的推理步骤。
• 过程奖励模型训练：作者开发了一个更有效的过程偏好模型（PPM），而不是简单的步骤级评分注释。该模型评估推理步骤的质量，引导政策SLM产生更好的解决方案。
• 自我演变框架：政策SLM和PPM从头开始构建，并通过多个回合进行迭代演变。在每一轮中，为大量数学问题生成数百万个合成解决方案，逐步增强模型的推理能力。

重要的是要注意，尽管LLM可以为给定问题提供正确答案，其推理可能存在缺陷或包含无效步骤。因此，模型必须能够学习如何在过程中避免无效步骤。rStar将推理分解为生成-区分过程。接下来的部分将讨论用于训练和改进LLM的技术。

技术

rStar的流程涉及生成替代步骤并对其进行推理。主要技术包括：

• 蒙特卡罗树搜索 (MCTS)：MCTS 在测试时用于探索多条推理路径。政策SLM生成潜在步骤，PPM评估它们，引导搜索朝着最有希望的解决方案前进。MCTS的使用是因为它将问题分解为单步生成任务，从而为LLM提供逐步的训练数据。此外，与一次生成完整解决方案要求的Best-of-N或自一致性相比，这种方法更简单。
• 代码增强数据合成：通过将代码执行纳入数据合成过程中，系统确保生成的推理步骤可验证且正确，为政策SLM提供高质量训练数据。
• 过程偏好建模 (PPM)：PPM评估中间推理步骤的质量，使系统在MCTS探索过程中偏好更合乎逻辑和准确的路径。
• 自我演变策略：通过迭代训练轮次，政策SLM和PPM都得到改进。每轮使用之前迭代的输出以提高性能，使模型能够随着时间的发展培养出高级推理能力。

MCTS是一种用于复杂领域的决策算法，例如棋类游戏（围棋、国际象棋、将棋）、组合优化和各种规划问题。MCTS的核心思想是通过从给定状态运行许多模拟“回合”（或回放）逐步构建搜索树，并使用模拟结果来指导应该更深入地探索树的哪个部分。MCTS的四个步骤是：

• 选择：从根节点（当前游戏状态）开始，根据平衡探索（尝试较少访问的移动）和利用（专注于看似有前途的移动）的选择策略选择子节点。树的上置信界（UCT）是一个标准选择策略。
• 扩展：当到达不是终端状态且有未访问子状态（移动）的节点时，扩展树中的一个（或多个）子节点。
• 模拟（回放）：从扩展的节点开始，模拟一系列随机（或半随机）移动，直到达到终端状态（即游戏结束或对于非终端状态的预定义深度）。记录该模拟的结果（胜/负/平或其他奖励度量）。
• 回传：将模拟的结果回传到树中访问过的节点，更新统计数据（例如，总奖励、访问计数）。该信息用于通知下一步选择。

在这种情况下，LLM首先生成一组人类推理动作的MCTS，以构建更高质量的推理轨迹，如：

• 提出一步思考。
• 完成推理思考。
• 提出子问题并回答。
• 重新回答子问题。
• 改述问题。

这些是我们作为人类解决复杂任务时的典型动作。我们重新表述或找到相关问题，这可以帮助我们对问题进行更深入的思考。

第二个LLM验证由第一个LLM提出的每个轨迹并评估其有效性。如果两者之间有一致性，轨迹可以被认为是相互一致且有效的。这类似于同伴之间的工作以及相互检查答案。由于每个步骤包含Python代码，因此仅保留成功执行代码的节点。这些高质量的轨迹将作为训练集的一部分。

作者提出了一种方法，提供逐步验证的轨迹以及逐步Q值注释。他们使用四轮自我演变：前两轮是终端导向MCTS（因为PPM尚未训练），而后两轮依赖训练好的PPM。从树根（原始查询）开始，LLM生成不同的替代步骤，并为每个步骤标注Q值。该过程继续，直到LLM找到对应于树叶的解决方案s_d。每个s_d包含一系列链接到根的步骤，对应于单个轨迹。最初，所有Q值都设为0。我们生成树的每个新层，直到我们到达第一个叶子（终端节点）并根据其是否得到正确答案进行奖励。然后，这个得分被反向传播到轨迹中的所有步骤，根据Q(s_k) = Q(s_k) + Q(s_d)。随着通过节点的有效轨迹增多，其Q值越高。最后，LLM选取n条高质量轨迹作为训练数据。

树的上置信界（UCT）平衡探索和利用。对于节点k，其UCT值的计算为：

$$ UCT(k) = \frac{W_k }{N_k} + c \sqrt{\frac{\ln (N_p )}{\ln (N_k )}} $$

其中W_k是节点k的总奖励，N_k是节点k被访问的次数，N_p是节点k的父节点被访问的次数，c是一个常数。较高的c值有利于探索。第一个项关注节点的奖励（利用），而第二个项通过对相对其父节点的高访问次数进行惩罚来鼓励探索。奖励最初将来自终端，随后由PPM提供。作者基于正负偏好对引入了一种新颖的训练方法。

由于SLM的能力较弱，作者采用四轮MCTS深度思考以生成逐步高质量数据，并为训练集扩展更多复杂问题：

• 第一轮：启动初始强政策模型，SML-r1。使用终端注释Q值并为效率执行8 MCTS回溯。得到的数据用于训练PPM-r1。
• 第二轮：训练可靠的PPM PPM-r2。使用PPM-r1，作者进行了大量MCTS，每个问题进行了16次回溯。
• 第三轮：PPM增强的MCTS以提高数据质量。使用PPM-r2，模型处理更复杂的问题并生成额外的数据以训练PPM-r3。
• 第四轮：解决更具挑战性的问题。对于未解决的问题，作者将回放次数增加到64或128次，并产生不同初始种子的各种MCTS。这一步提高了数学模型的成功率。

结果

在四轮自我演变后，rStar-Math显著提高了SLM的数学推理能力。例如，在MATH基准测试中，它将Qwen2.5-Math-7B的性能从58.8%提升至90.0%，Phi3-mini-3.8B的性能从41.4%提升至86.4%，超越了OpenAI的o1-preview模型。此外，在美国数学奥林匹克（AIME）中，rStar-Math解决了平均53.3%的问题，排名在高中数学学生的前20%。下图比较了rStar-math在不同基准测试中与其他LLM的表现，基于回放数量。

总结

LLMs在理解人类语言、图像生成和开发执行各种任务的代理方面展现了巨大的能力。尽管其性能和准确性有所提升，但这要以需要更多参数为代价，增加了训练和推理成本，使用户无法在本地运行或微调它们以执行特定任务。另一个重要点是，LLMs可能会产生幻觉，提供无效的答案或以有缺陷的推理给出正确答案。本文探讨了如何使用深度思考与小型LLM来提高性能，这可能使用户能够在本地运行模型，甚至对其进行微调。通过使用蒙特卡罗树搜索、基于围棋引擎的评分策略和代码增强数据，rStar-math实现了类似于大型LLMs的性能。总之，rStar-Math证明，通过创新的训练和推理策略，小型语言模型能够在数学推理任务中达到先进水平的性能，与大型模型相抗衡或超越。

• 原文链接： blog.lambdaclass.com/sum...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～