探索自动化做市商 (AMM)

这篇博文受到了这篇研究论文的强烈启发，主要汇总了其内容。为了提高可达性，进行了少量修改和补充。

目录

• 介绍
• 基础 AMM 经济学
• 机制的形式化
• 广义公式
• AMM 协议比较
• AMM 安全考虑

介绍

AMMs 代表 自动化做市商，是 去中心化交易所（DEXs）的基础组成部分。

它们通过使用 一种算法性确定价格的对池方法 革新了人们交易资产的方式，而不是通过传统的订单簿匹配买卖双方。这使得 AMM 容易去中心化、自动化并且持续运行。

除了这些特性外，AMMs 还有一些 缺点：对交易者而言可能存在高 滑点，对流动性提供者而言存在 非永久性损失。

滑点定义为 交易现货价格和实现价格之间的差异。相对于可用流动性，从池中提取的资产数量越大，滑点就越大。

非永久性损失定义为 池中资产的价值与其在池外持有时的价值之间的差异。其原因在于池不断重新平衡其资产数量，以保持每个资产的价值相等。如果资产 A 相对于资产 B 贬值，池将“自动”增加 A 的数量，同时减少 B 的数量，直到它们的价值相匹配。

这些缺点 源自于 AMMs 中实现的算法的特性：价格沿着由池中资产数量决定的预定义轨迹移动。

Uniswap 是最常用的 AMM，其推出了常量乘积公式 作为协议的基础：该 池 由两种不同资产 A 和 B 组成，以数量 $r_A$ 和 $r_B$ 的代币初始化，以便 $r_A/r_B$ 等于价格关系 A/B。 然后，池中的每一项操作必须始终满足一组守恒函数不变式。最简单且最著名的是 Uniswap 的常量乘积公式 $x.y = k$，其中 $x$ 和 $y$ 等于 $r_A$ 和 $r_B$。

基础 AMM 经济学

参与者

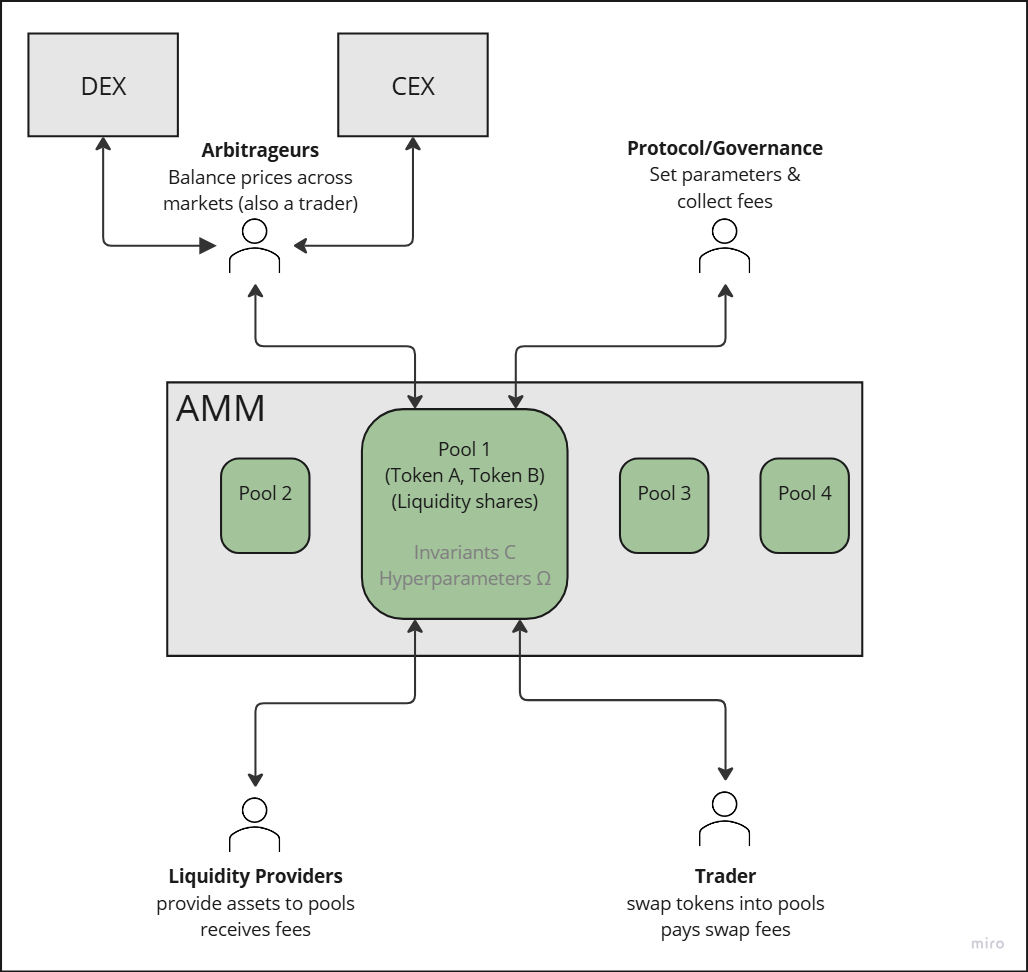
4 名主要参与者 在 AMM 生态系统中互动：

• 流动性提供者（LPs）： 向池提供流动性，允许其他用户进行交易。他们获得代表其存款价值的份额，可以在操作时放弃以获取相应数量的流动性。
• 交易者： 这些用户与池进行交易，并支付指向 LP 和协议的费用。
• 套利者： 比较不同平台（DEX、CEX 等）中的价格资产，以通过价格差异寻找利润机会。此机制确保资产价格的一致性。
• 协议/治理： 通常通过费用获得报酬，因此在财务上激励其为每一方提供最佳体验。

资产

我们还可以找到 4 种类型的资产：

• 风险资产： 主要类型的资产；这些是 AMM 为交易者提供流动性的资产，感谢流动性提供者。
• 基础资产： 当前很少见，但某些协议有风险/基础资产的池。 例如，每个 Uniswap V1 池的基础资产为 ETH，Bancor 以其自身的代币 BNC 作为基础资产。但现如今，许多 AMM 仍遵循类似模式，池中的一方是稳定币（USDC/USDT/DAI）或 ETH/WETH。
• LP 份额： 在池中存入时铸造给流动性提供者。份额代表对池中部分的所有权。
• 协议代币： 通常作为奖励分发，以激励用户执行有利于协议的特定操作。有时作为治理代币，或者给持有者提供优势。大多数可以公开交易。

奖励

AMMs 通常使用这些奖励作为激励，鼓励参与和贡献：

• 流动性奖励： 这些来自交易费用，分发给流动性提供者。它们是对资产被锁定的补偿方式。
• 治理权： 协议代币通常为了激励协议中的某些操作（例如交易、流动性提供、质押）而分发。
• 质押奖励： 质押协议代币以获得另一种奖励（例如，交易者更少的费用，LPs 更多的费用）。

明确成本

与 AMMs 互动会产生各种成本，既可作为产生收入的方式，也可激励特定行为：

• 交易费用： 向与流动性池互动的交易者收取，以补偿流动性提供者提供资产的费用。费用的一小部分也可以被作为协议收入收取。
• 流动性撤回罚金： AMMs 希望激励长期和均衡流动性，因此可以应用减少奖励或甚至收费的形式来实施惩罚。
• Gas 费用： 本质上是该协议所托管的链上固有的费用。

隐性成本

这些成本被视为隐性成本，因为它们是从设计本身产生的，而不是刻意实施的。

• 滑点： 没有交易执行和预期价格之间的差异。源于守恒函数不变式的非线性。常量和 AMM 不会遭受滑点。
• 非永久性损失： 当资产在池外和池内持有时的价值差异。也源于守恒函数不变式，其自动重新平衡资产，以保持它们之间的相对价值。

机制的形式化

区块链通常被建模为状态转移系统。在这种表示中，池有一个状态，可以通过以下参数描述：

• $r_k$ : 代币 $k$ 的 数量（储备），对于 $k=1,...,n$，其中每个 $k$ 代表不同的代币
• $p_k$ : 代币 $k$ 的 价格
• $C$ : 守恒函数不变式。管理如何进行交易的数学规则，比如 Uniswap 著名的常量乘积公式。
• $\Omega$ : 一组协议 超参数（例如，买入/卖出费用）

一些协议将相同的 $C$ 或 $\Omega$ 应用于每个池（例如 Uniswap V2），而 其他协议将允许对池的配置有更多粒度的控制（Uniswap V3/4、Curve、Balancer 等）。

当 $r_k$ 和 $p_k$ 随着池中的几乎每个操作变化（交易、流动性提供）时，$\Omega$ 通常是 在池创建时固定的，而 $C$ 的定义是在整个池期间 保持不变（尽管交易费用可以改变它）。

我们仍然可以从 AMMs 得到这些 一般规则：

• 代币 $p_k$ 的价格在 纯 流动性提供/撤回时保持不变
• 不变性在 纯 交换活动中保持不变

纯粹 意味着我们没有考虑费用，因为它们 暗示了额外的操作：

• 首先是交换 - 给定数量 $x_1$，我们计算必须返回的数量 $x_2$，同时保持池不变式。
• 然后是费用 - 从 $x_2$ 中扣除，交易者收到 $x_2 - f$，而 $f$ 保留在池中。 虽然第一个操作确实保持了不变性，但第二个则没有。

最后，只有当资产的存入 与当前储备比（$r_1/r_2$）成比例时，代币的价格才能保持不变，因为价格直接源于这些参数。

广义公式

交换

在储备 $(r_1,r_2)$ 的池中，将 $x_1$ 代币交换为 $x_2$ 代币可以分解为以下步骤： 1) 池接收 $x_1$ 并更新储备数量：

• $r_1'=r_1 + x_1$ 2) 使用守恒函数不变式 $C$ 计算新的储备 $r_2'$：
• $r_2' = f(x_1, {r_k}; C)$
  3) 将差额发送给用户：
• $x_2=r_2 - r_2'$

滑点

滑点测量实现价格 $x'_1/x'2$ 与交换发生之前的现货价格 $p{1/2}$ 之间的偏差

$$S(x_1,{r_k};C) = \frac{x'_1/x'2}{p{1/2}} - 1$$

非永久性损失

非永久性损失测量资产在池中的价值与它们如果在池外持有的价值之间的差异。

$$IL = \sum\limits_k \frac{x_k^o.r_k}{x_k.r_k}-1$$

其中 $x_k^o$ 是存入时的资产数量，而 $x_k$ 是评估时池中的资产数量。

AMM 协议比较

Uniswap V2

• 流动性池总是由恰好两个资产组成
• 协议假设两个资产的储备始终具有相同的价值：$r_1 . p_1 = r_2 . p_2$
• 守恒函数不变式：$$C= r_1.r_2$$
• 此不变函数仅在纯交换时得到验证，费用的扣除会改变该不变性，变为：$$C \ge r_1.r_2$$

Uniswap V3

• Uniswap V3 通过允许流动性提供集中在两个选择价格之间的曲线一段（也称为 ticks）来增强 V2。这意味着曲线的每个段都有其自己的 $C$。
• 在特定曲线（价格范围）上增加流动性可以减少那个范围内的滑点。
• 整个曲线的守恒函数不变性只是复杂的。
  • 但如果我们看活跃 tick 范围的 C，与 Uniswap V2 相同。
  • 对于所有其他 tick 范围，流动性是单侧的（仅可用一种资产）。

Uniswap V4

• Uniswap V4 AMM 继承自 Uniswap V3，功能相同。
• 但是增加了一个新概念：Hook。
  • Hooks 是在特定操作之前和之后可调用的函数：流动性更新、交换等等。
  • Hooks 可以重写 AMM 的整体逻辑，使开发人员能够实现自定义的不变性。

Balancer

• Balancer 允许每个池有超过两个资产。每个资产储备 $r_k$ 在池创建时被赋予权重 $wk$，其中 $\sum\limits{k}w_k = 1$
• 权重是一个超参数，在交换/存入时不会改变，它们表示该资产的储备在池中必须维持的价值百分比。
• Balancer 提供不同类型的池
• 其中一个称为 流动性引导池 允许在时间上配置变化的权重。
• Uniswap 是其特殊情况，$w_1=w_2=\frac{1}{2}$。
• 守恒函数不变式：$$ C = \prod\limits_{k}r_k^{w_k}$$

Curve

• 在 Curve 中，流动性池支持两种或多种具有相似Hook的资产。
• 类似于 Balancer，Curve 提供不同类型的池，这通过一个称为放大系数 $A$ 的超参数来控制，它基本上定义了曲线是如常量乘积还是常量和行为。
  • 当 $A\to 0$ 时，常量和项在常量乘积项面前消失。
  • 当 $A \to \infty$ 时，常量和占据公式。
• 守恒函数不变式：$$A(\frac{\sum_{k}rk}{C}-1) = \frac{(\frac{C}{n})^n}{\prod{k}r_k}-1$$

AMM 安全考虑

这篇研究论文的这部分探讨了不同的攻击情况，但远不止于此。如果你想进一步了解 AMM 的漏洞，我建议你查看这篇很好的文章。

闪电贷攻击

以下示例与原示例不同，因为第 2 步在新价格上存在错误

在一个由 2 个代币组成的池中，$token_A$ 和 $token_B$ 具有储备 $r_A$ 和 $r_B$：

1. 借用 来自 CDP 协议的 $x_A$ 代币 $token_A$，使得 $x_A.p_A = x_B.p_B$（其中 $p$ 是代币按照名义货币的价格，或者为简单起见以美元计）处于市场价格。
2. 交换 $x_A$ 代币 $token_A$ 为 $\alpha .x_B$ 代币 $token_B$ 在 AMM 中。
   • 这将把价格 $p_{A/B}$ ($token_A$ 以 $token_B$ 计) 向下推至 $\frac{r_B -x_B - \Delta_1}{r_A + x_A}$。
3. 借用，从另一 CDP 协议中使用 AMM 作为唯一价格预言机，借用 $x_A + \Delta_2$ 代币 $token_A$ 以及在步骤（2）获得的 $\alpha .x_B$ 代币 $token_B$。
   • 因为 $p_{A/B}$ 已经压低，现在 $token_A$ 的价值降低，使得可以借用比步骤（1）更多的 $x_A$。
4. 偿还 闪电贷的 $x_A$ 代币 $token_A$。
   • 利润等于 $\Delta_2$（减去手续费）。

这类攻击可以通过使用 TWAP 或去中心化预言机网络（例如 Chainlink、Pyth）来解决。

地毯抽走

1. 铸造 新代币 XYZ。
2. 创建 一个池，其中 $x{XYZ}$ 代币 XYZ 和 $x{ETH}$ 代币 ETH（也可以是其他代币）。
   • 现在有一个储备为 $R=(r{XYZ}; r{ETH})$ 的池。
   • 收到流动性提供代币用于存入的流动性。
3. 吸引人们 来购买 XYZ 代币。
   • 这将使池的储备更改为 $R'=(r'{XYZ}; r'{ETH})$。
   • 其中 $r'{XYZ} = r{XYZ} - \Delta r{XYZ}$ 和 $r'{ETH} = r{ETH} + \Delta r{ETH}$。
   • 因此，池中的 XYZ 会减少，而 ETH 会增加，因为人们购买了 XYZ。
4. 通过交付 LP 代币撤回流动性，并获得：
   • $x'{XYZ} = x{XYZ} - \Delta_{1}$。
   • 而且 $x'{ETH} = x{ETH} + \Delta_{2}$。
   • 其中 $\Delta{1}, \Delta{2} > 0$。 5) 交换 剩余的 XYZ 代币以获得更多的 ETH。

AMMs 和上升平台协议可以通过强制流动性在一段时间内被锁定而无法撤回来缓解这一问题。

价格三明治攻击

1. 用户 A 希望购买现货价格为 $p_1$ 的 $x_A$ XYZ 代币，使用带有 GAS 费用的 AMM。
2. 用户 B 查看了记忆池中的交易，并通过支付更高的 gas 费用来抢先购买 XYZ。
3. 用户 B 和 A 的交易分别以 $p_B$ 和 $p_A$ 的平均价格依次执行，导致 XYZ 的现货价格上涨至 $p_2$，其中 $p_2 > p_A > p_B > p_1$，这是由于滑点造成的。
4. 用户 B 回补，通过在价格 $p_B'$ 下卖出 $x_B$ XYZ 代币，在此 $p_2 > p_B' > p_B$，因滑点所致。
5. 用户 B 的利润为 $profit = x_B.(p_B' - p_B)$，减去费用。

有多种方法可以缓解这种类型的攻击：

• 允许用户 A 设置滑点参数，尽管这只会减少损失，但最大损失将是可配置的。
• 一些协议，如 CoW Swap 创建替代记忆池，激励区块构建者将大部分滑点重新分配给交易者。
• 一些 L2 拥有私有记忆池，使得这种攻击几乎不可能。

夹击 LP 攻击

1. 用户希望以 $x_B$ 的 $tokens_B$ 在包含 $r_A$ 和 $r_B$ 代币的 AMM 池中购买 $x_A$ 的 $tokens_A$ 。
2. LP 看到用户的交易，并通过撤回 $k.r_A$ 和 $k.r_B$ 代币（$k<1$）来抢先交易。
   • 池的流动性低于之前，从而增加滑点的效果。
   • 储备量变为 $r_A' = (1-k).r_A$ 和 $r_B' = (1-k).r_B$。
3. 用户的交易随后以比预期更糟的执行价格执行。
   • 此时池的储备是 $r_A' = (1-k).r_A - x_A$ 和 $r_B' = (1-k).r_B + x_B$。
4. LP 回补流动性到池中：
   • 对于 $tokens_A$，他提供 $k.r_A$。
   • 对于 $tokens_B$，他提供 $k\frac{r_B'}{r_A'}$，这个值是根据新的 AMM 价格计算的。
5. LP 仍然拥有 $x_B - k\frac{r_B'}{r_A'}$ 的 $tokens_B$ 并将其交换为一些 $tokens_A$，确保获利。

感谢你阅读这篇博文。

如果你喜欢这篇文章，你可能想查看原始论文，更多详细信息可在顶部找到。

• 原文链接： github.com/InfectedIsm/B...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～