深入理解区块链常用数据结构

  • Dapplink
  • 发布于 2025-01-22 21:36
  • 阅读 77

深入理解区块链常用数据结构

一、本节概述

  • Merkle树
  • 前缀树
  • MPT树
  • MPT的应用布隆过滤器

二、Merkle树

1. Merkle树简介

Merkle树: 结合了 Binary tree 和Hash Pointer数据结构，在比特币 merkle root Hash

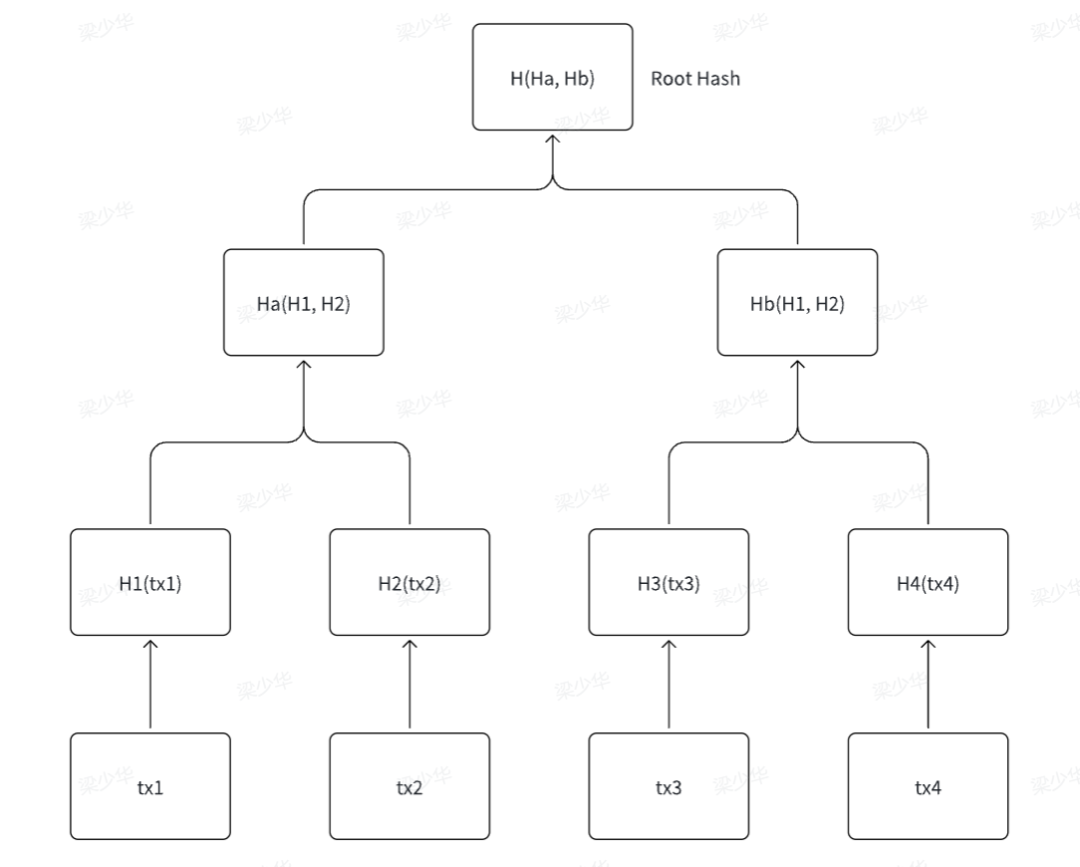
fa7e6d47e66da2ae249a90c39216574f.png

  • 不断两两 Hash，最终得到一个根Hash
  • 应用场景
    • 交易防篡改
    • 可以验证数据是否存在在这个结构

2. Merkle Tree 在比特币中的应用

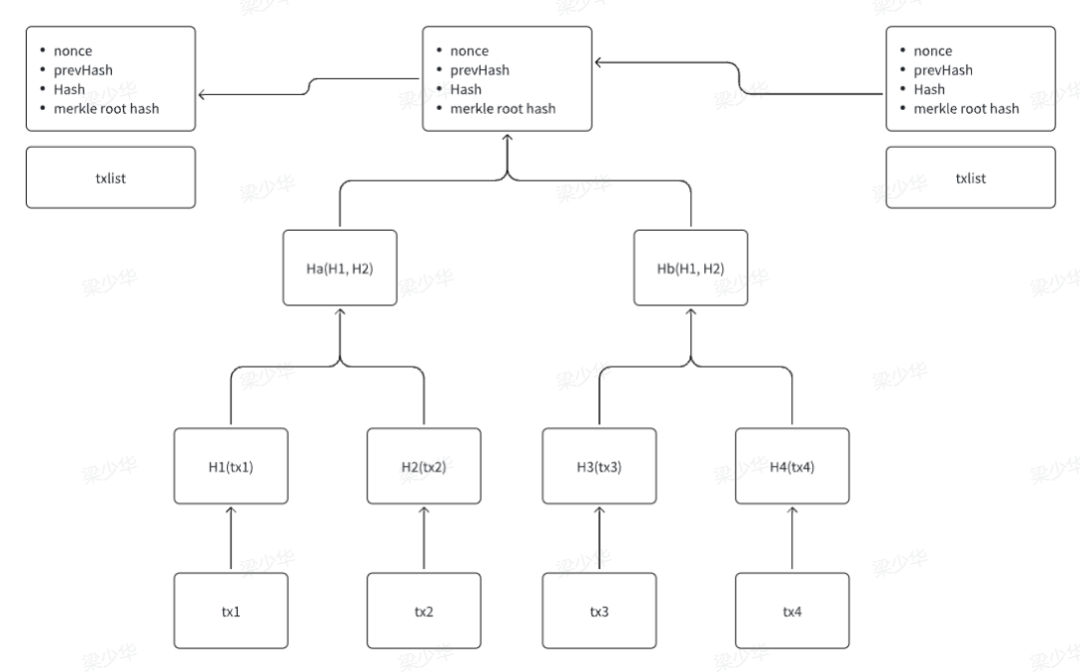
d4c14fff17d2153227f6f9c0c1cb71f7.png

3. Merkle Tree 的其他应用场景

  • 空投合约里面进行空投的数据
  • Celestia 使用命名空间的 merkle tree 验证数据的准确性
  • Taproot merkle 抽象语法树

三. 前缀树

前缀树(字典树)：用来保存关联数组，它的键通常是一个字符串，前缀树的节点在树中的位置是由其键的内容决定，前缀树的Key是编码在根节点到该节点的路径中。

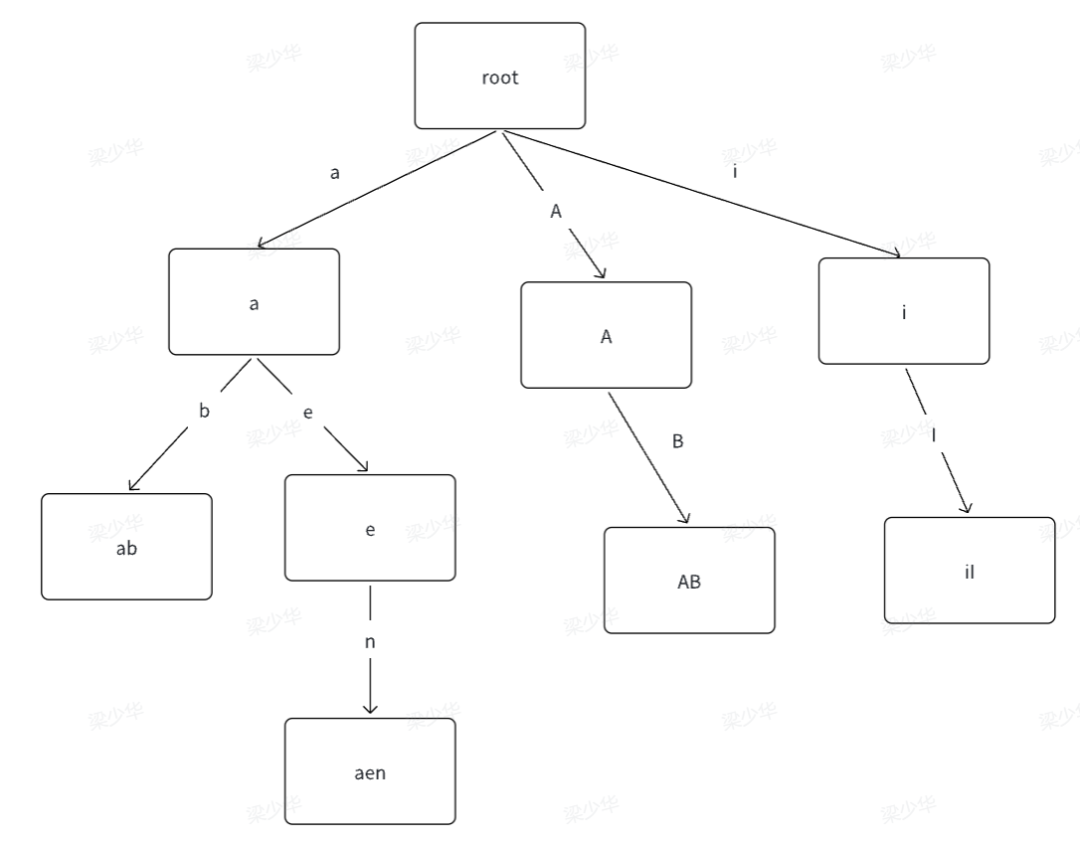
ef4db786e2859f1799f29cb9b34830ca.png

在上图中共有 4 个叶子节点，分别是 ab, aen, AB, iI

1. 前缀树的优势

  • 相比Merkle,  使用前缀树来进行查询用拥有共同前缀 Key 的数据时是十分高效，但是最差的情况，仍然需要遍历整个树，复杂度O(n),  对于前缀树来说，它的效率是merkle 树比高很多。

    2. 前缀树的缺点

  • O(n), n次的 IO 开销，相比于直接查找，对磁盘的压力比较大
  • 当Key比较长时，可能会造成空间的浪费

四. MPT树

  • MPT树：是一种改良的，融合了默克尔树和前缀树两种树结构优点的数据结构，是以太坊中用来管理状态，交易，收据的数据结构。

    1. MPT 树的作用

  • 可以存储任意长度的key-value的键值对数据
  • 提供了一种高效快速计算维护数据集Hash标志的机制
  • 提供了快速状态回滚机制
  • 提供了一种称为Merkle的机制，进行轻节点验证扩展

在以太坊中，为MPT树新增了几种不同类型的树节点，以尽量压缩树高，降低操作的复杂度MPT 树中有四种类型的节点

  • 空节点
  • 分支节点
  • 叶子节点
  • 扩展节点

1.1 空节点

空节点用来表示空串。

1.2 分支节点

分支节点（Branch Node）是MPT树中拥有两个及以上子节点的非叶子节点，通过Nibble编码降低存储开销，同时增加树的高度。 它包含16 个子节点指针，以及存储自身值的额外字段，并使用 nodeFlag 记录哈希、脏标志和生命周期信息，优化性能和内存管理。 定义如下所示：

type fullNode struct {    
    Children [17]node    
    flags    nodeFlag
}
type nodeFlag struct { 
    hash  hashNode // cached hash of the node (may be nil)  
    gen   uint16   // cache generation counter  
    dirty bool     // whether the node has changes that must be written to the database
}

分支节点用于表示MPT（Merkle Patricia Trie） 树中所有拥有两个或以上子节点的非叶子节点。

类似于前缀树，MPT也将键（key）编码到树的路径中。然而，以太坊中的键值范围较大（[0-127]），因此，在进行树操作前，会先对key进行编码转换：

  • 每个字节的高4位和低4位被拆分成两个单独的Nibble（半字节）存储。
  • 这样，转换后的键 key' 的每个字符值范围变成 [0, 15]，使得每个分支节点最多拥有16个子节点。

这种编码方式降低了每个分支节点的存储需求，但增加了树的高度。 分支节点的结构：

  • 子节点列表（长度 16）：最多存储16 个子节点（每个代表一个 Nibble）。
  • 最后一个元素（第 17 项）：用于存储自身的值，即当前路径存储的 value（若存在）。

附加字段：nodeFlagnodeFlag 记录了一些辅助信息：

  • 节点哈希（Node Hash）：若不为空，可直接使用上次计算的哈希，避免重复计算当节点内容发生变化时，该字段被置空，触发重新计算
  • 脏标志（Dirty Flag）当节点被修改时，该标志置为 1，标记为脏数据
  • 诞生标志（Birth Flag）：当节点首次被载入内存或被修改时，赋予一个计数值，作为清理机制的依据用于定期清理 “老旧且未修改” 的节点，防止占用过多内存

1.3 叶子节点（Leaf Node）和扩展节点（Extension Node）

在 Merkle Patricia Trie（MPT）中，叶子节点（Leaf Node）和扩展节点（Extension Node）具有相似的结构，均由 shortNode 结构体表示：

type shortNode struct {
    Key   []byte
    Val   node    
    flags nodeFlag
}

其中关键的字段为：

  • Key：存储该节点所覆盖的Key前缀。
  • Val：存储该节点的内容（数据值或子节点）。
  • flags：用于存储节点元数据（如哈希、脏标志等）。

叶子节点（Leaf Node）

  • 作用：存储完整的Key路径和最终的Value。
  • 特点：
    • Key：存储的是完整的剩余路径。
    • Val：存储的是 实际的value（终端数据）
  • 终止条件：到达叶子节点后，不再向下遍历。

其中Key是MPT树实现树高压缩的关键！

1.3.1 Merkle Patricia Trie（MPT）的路径压缩优化 在标准的前缀树（Prefix Tree）结构中，由于每个字符（或部分键）都需要一个单独的节点，因此可能会导致大量的存储空间浪费。MPT通过路径压缩（Path Compression） 解决这一问题，减少冗余节点，提高存储和查询效率。

1.3.1.1 MPT 的路径压缩优化 问题：在普通前缀树中，如果插入的键 toast，但当前树结构中并不存在以 t 开头的路径，则需要逐个创建节点 来存储 t → o → a → s → t。这会导致：

  • 存储空间浪费：大部分非叶子节点只是路径的一部分，并不存储实际数据。
  • 查询效率低：查询 toast 需要遍历多个无效节点，导致更多的磁盘访问（I/O）。

MPT解决方案：   

  • 当插入一个键时，如果发现没有现有路径与该键的前缀匹配，则直接将剩余的键存储在叶子节点（Leaf Node）或扩展节点（Extension Node）的Key字段中，而不创建冗余路径。 
  •  这样，叶子节点和扩展节点的Key充当了一种“Shortcut”，减少不必要的层级，提高查找效率。

1.3.1.2 示例分析假设我们插入以下两个键：

  • toast
  • top

普通前缀树（未优化）：

t  
|   
o  
|   
a  
|   
s   
|  
t  (存储值)

如果再插入 top，它将从o节点开始创建新的分支，最终形成：

t   
├── o  
│   ├── a → s → t  (存储 "toast" 的值)  
│   └── p  (存储 "top" 的值)

可以看到toast和top共享前缀 to，但仍然需要单独创建多个节点。

MPT经过路径压缩后的结构：

t → o       
    ├── ast (存储 "toast" 的值)    
    └── p   (存储 "top" 的值)

在这里： 

  • to 作为扩展节点（Extension Node），指向两个子路径 
  •  ast 直接存储在叶子节点中，而不是拆分为多个单独的字符节点。

1.3.1.3 扩展节点（Extension Node）和叶子节点（Leaf Node）在数据库中的存储在 MPT 中，每个扩展节点和叶子节点的Val 字段可以存储：

  • 哈希索引（存储在数据库中的节点索引值）
  • 直接引用（指向内存中的子节点）

这种设计的原因：

  • 如果整棵MPT持久化到数据库，则必须存储子节点的哈希索引，确保持久化后的树结构仍然可被解析。
  • 如果数据在内存中，可以直接使用指针引用，避免额外的数据库查询，提高访问速度。

优点：

  • 保持父子节点的关联，即使树存储在数据库中，也能通过哈希索引找到子节点。
  • 减少磁盘 I/O：   
    • 如果当前节点已包含所需数据，则无需再读取子节点。 
    •   如果当前节点需要更多数据，则递归查询子节点的哈希索引。

1.3.1.4 如何区分Val字段存储的是数据还是哈希索引？在以太坊的MPT实现中，通过Key中的特殊标志来区分：

  • 叶子节点（Leaf Node）：Val存储的是最终的数据值。
  • 扩展节点（Extension Node）：Val存储的是子节点的哈希索引。

以太坊采用Nibble（半字节）编码，并在Key的第一个字节添加前缀来区分：

Key 前缀 含义
0x00 / 0x01 扩展节点（Extension Node）
0x02 / 0x03 叶子节点（Leaf Node）
  • 如果 Key = 0x03 | "ast"，表示：   0x03（叶子节点标志）   ast（存储路径）   Val 存储的是最终的数据值。
  • 如果 Key = 0x01 | "to"，表示：   0x01（扩展节点标志）   to（存储路径）   Val 存储的是子节点的哈希索引。

2. 以太坊 MPT（Merkle Patricia Trie）中的 Key 编码方式详解

在以太坊的MPT（Merkle Patricia Trie）树中，Key 的编码主要有三种不同的形式，分别用于不同的场景： 编码方式 用途 ** 示例（key=“cat”）
Raw编码 MPT对外提供的默认编码方式（无变换） ['c', 'a', 't']（ASCII: [63, 61, 74]）
Hex编码 MPT内部对Key进行扩展存储的方式（拆分高 4 位和低 4 位） [3, 15, 3, 13, 4, 10, 16]
HP（Hex-Prefix） 编码数据库中存储Trie节点的编码方式（Hex 编码基础上加入前缀标志） [32, 63, 61, 74]

2.1 Raw 编码

定义：Raw 编码就是未经转换的原始Key，它是MPT对外接口默认使用的编码方式。存储方式：直接存储 Key 的字符，不做任何转换。示例：如果 key 为 "cat"，其 Raw 编码 为：

['c', 'a', 't']

换成 ASCII 数值：

[63, 61, 74]  // ASCII of 'c' = 63, 'a' = 61, 't' = 74

2.2 Hex 编码

为了优化MPT的存储结构，以太坊使用Hex 编码（16 进制扩展编码）： 原因：原始Key的每个字符（byte）范围是[0-127]，这样会导致分支节点需要128 个子节点。为了减少存储空间，以太坊对 Key 进行转换：

  • 每个字符（byte）拆分为 两个Nibble（半字节, 4-bit），使其值范围变成 [0-15]（即 16叉Trie）。
  • 这样，每个分支节点最多只有16个子节点，大大减少了存储空间。

Hex 编码转换规则：

  • 拆分每个字节的高4位和低4位，分别存储：    例如 "c"（ASCII 0x63），拆分成 0x6 和 0x3
  • 如果该Key对应的节点是叶子节点（Leaf Node），则在末尾添加0x10作为终止标记；
  • 如果该Key对应的是扩展节点（Extension Node），则不添加终止标记。

Hex 编码转换示例

  • 如果Key为 "cat"，其ASCII码值分别为： 
    'c' -> 0x63
'a' -> 0x61
't' -> 0x74

拆分成高4位和低4位：

'c' -> 0x6  0x3
'a' -> 0x6  0x1
't' -> 0x7  0x4

然后转换为Hex编码：

[3, 15, 3, 13, 4, 10, 16]  // 最后 16 代表叶子节点终止符

Hex 编码用途

  • Hex 编码用于 Trie 内部存储，以减少存储空间，提高查询效率。

2.3 HP（Hex-Prefix）编码

问题：

  • 在MPT中，叶子节点（Leaf Node）和扩展节点（Extension Node）共享相同的数据结构。
  • 但是，当树存储到数据库中时，需要区分这两种节点类型，因此以太坊引入了
  • HP编码（Hex-Prefix 编码）。HP编码用于数据库存储的Trie节点Key

HP 编码转换规则

  • 如果Key末尾为0x10（表示叶子节点），去掉这个标记
  • 在 Key 之前添加一个前缀半字节（Nibble）
  • 最低位（LSB, Least Significant Bit）：      记录原 Key 长度的
  • 奇偶性:      奇数长度 → 1  偶数长度 → 0   低 2 位编码终止标记：叶子节点（Leaf Node） → 1扩展节点（Extension Node） → 0如果 Key 长度是奇数，在 Key 之前再增加一个 0x0 的半字节Hex 编码转换回字节存储（逆转换）

HP 编码转换示例如果 Hex 编码 为：

[3, 15, 3, 13, 4, 10, 16]

进行HP编码转换：    去掉末尾16（叶子节点终止标志）：

[3, 15, 3, 13, 4, 10]
  • 确定 Key 长度的奇偶性：  Key 长度 = 6（偶数），最低位 = 0    叶子节点，终止标记 = 1  因此前缀半字节 = 0b0010（即 0x2）
  • 重新编码回字节存储
[32, 63, 61, 74]
  • 0x2 → 代表偶数长度的叶子节点
  • 0x3F → 原始Key的编码
  • 0x3D
  • 0x4A

HP 编码用途

  • HP编码用于数据库存储，确保持久化后的MPT节点可以正确区分叶子节点和扩展节点。
  • 当Trie节点从数据库加载到内存时，HP编码会被转换回Hex编码。

2.4 三种 Key 编码的转换关系

Raw 编码（原始 Key）  ——>  转换成 Hex 编码（用于 MPT 内存存储）  ——>  转换成 HP 编码（用于数据库存储）                                
            （当数据项被插入到 MPT 时）                                
            （当 MPT 节点被持久化到数据库时）                                
            （当 MPT 节点从数据库加载到内存时）

8cd3eac8b3b29b763a6f94b0987f6401.png

3. 安全的Merkle Patricia Trie（MPT）

在标准的MPT（Merkle Patricia Trie）中，Key可以是任意长度的字符串，这会导致：

  • 树的深度无限增长，影响查询性能；
  • 易受DoS攻击，攻击者可以构造极端情况拖慢SLOAD操作；
  • Key以明文存储，缺乏隐私保护。

为了解决这些问题，以太坊对MPT进行了封装优化，即使用Key的哈希值 sha3(key) 作为MPT存储的实际 Key。

3.1 MPT直接存储明文Key的问题

在原始 MPT 设计中：

  • Key 没有限制，可能很长，导致Trie变得非常深
  • 例如，如果存储以下数据项：
("aaaaaaaaa...", value1)
("aaaaaaabbb...", value2)

由于 Key 很长，会导致Trie的深度很大，查询需要遍历很多层，影响性能。 攻击者可以利用这一特性发动DoS攻击：

  • 通过存储特定模式的数据（如大量长 Key），构造单条长路径的MPT，让查询变得非常慢
  • 之后不断调用SLOAD（状态存储读取指令） 访问该数据，造成合约 Gas费用极高，拖慢整个以太坊网络。
  • Key 以明文形式存储，容易暴露隐私信息：   例如，存储账户地址0x1234... 作为Key，会暴露该账户的状态。

3.2 以太坊的安全优化：Key哈希化

3.2.1 方案 解决方案：在存入MPT之前，先对Key进行SHA3（Keccak-256）哈希计算：

MPT 真实存储的数据项：( sha3(key), value )

即：

  • 不再存储原始Key，而是存储其SHA3哈希值。
  • 示例
Key:   "cat" -> SHA3("cat") = 0x82a...f90
Value: "dog"
  • 最终存入 MPT 的数据项：
(0x82a...f90, "dog")

3.2.2 优势

  • Key 变为固定长度（32 字节）    避免了 Key 过长导致MPT深度增长的问题，提升查询性能。    MPT 树的深度保持稳定，提高存储效率。
  • 防止DoS 攻击：    由于 Key 经过哈希处理，攻击者无法构造超长路径来拖慢查询速度。    避免了 SLOAD 读取深层节点时的高Gas消耗问题。
  • 增强隐私保护：  原始Key不直接暴露，外部无法直接知道存储的数据Key是什么。例如：
sha3("Alice's Account") = 0xabc123...
sha3("Bob's Account")   = 0xdef456...

外部只能看到0xabc123...，而不会直接知道 “Alice’s Account” 的信息。

3.2.3 劣势 尽管该方法提高了安全性，但也引入了一些额外的开销： 每次存取数据时都需要计算sha3(key)：

  • 增加了一次哈希计算的CPU开销，略微影响性能。 需要存储sha3(key) → key的映射关系：
  • 因为以太坊智能合约执行时，用户可能只知道原始 Key，但MPT只存储了sha3(key)。
  • 因此，需要一个额外的数据库表来存储映射关系：
(key → sha3(key))

这样，在查询时，可以通过先计算 sha3(key)，再查找数据。

五. MPT的基本操作

1. Get操作（查找Key）

MPT的Get操作用于查找某个Key 对应的Value。其过程如下：

  • 将Raw编码的Key转换成Hex编码（每个字符拆成两个半字节，并在末尾加 0x10 作为叶子节点终止符）。
  • 从根节点开始，按照搜索路径查找： 
    • 扩展节点： 若当前节点是扩展节点，且存储的是哈希索引，则从数据库加载该节点，并递归调用查找函数    若当前节点的Key是搜索路径的前缀，则继续在子节点查找，否则该Key不存在。        
      • 分支节点：        若搜索路径为空，则返回分支节点的Value。      若搜索路径不为空，则按照搜索路径的第一个字节选择子节点，并递归查找。   
      • 叶子节点： 若叶子节点的Key与剩余搜索路径完全匹配，则返回Value。        否则，该 Key 不存在。

示例：查找 Key “cat”Key "cat" 的 Hex 编码为：

[3, 15, 3, 13, 4, 10, 16]  // 最后 16 表示叶子节点终止符
  • 从根节点开始搜索：    根节点是扩展节点，Key 为 [3, 15]，匹配搜索路径前缀 [3, 15]，继续搜索子节点，剩余路径为 [3, 13, 4, 10, 16]。  进入分支节点，搜索路径的第一个字节是 3，选择分支 3，继续搜索，剩余路径为 [13, 4, 10, 16]。  进入叶子节点，Key 为 [13, 4, 10, 16]，完全匹配剩余搜索路径，查找成功，返回 Value = "dog"。

2. Insert 操作（插入 Key-Value）

插入操作的步骤：

  • 先执行Get操作，找到与新Key拥有最长相同前缀的节点，记为 Node。
  • 根据Node类型进行插入：   
  • 分支节点： 若剩余搜索路径不为空，则插入新的叶子节点到合适的子节点位置。若剩余搜索路径为空（完全匹配），则更新分支节点的Value。
  • 叶子/扩展节点： 若剩余路径与当前节点的 Key 完全匹配，则更新 Value。 若不匹配：        创建新的分支节点，存放当前节点与新Key的共同前缀。 将当前节点和新节点作为两个子节点存入分支节点，并将当前节点转为扩展节点。
  • 标记被修改节点为 dirty，清空 hash，更新诞生标记。

示例：插入 Key “cau”

  • Hex 编码：
[3, 15, 3, 13, 4, 11, 16]  // "cau" + 终止符
  • 查找最长前缀节点（Node1）。
  • 创建新的分支节点 Node2，插入 cau 和 cat：
    • Node1 变成扩展节点。
    • Node2 成为分支节点，存储分支 [11]（“u”）和 [10]（“t”）。

3. Delete操作（删除 Key）

删除操作与 Insert 类似：

  • 先执行Get操作，找到Key最长匹配的节点Node。
  • 删除逻辑： 删除子节点，若删除后只剩一个子节点，则将其合并成叶子/扩展节点。 若搜索路径与 Node 的 Key 完全匹配，直接删除。 若不匹配，则 Key 不存在，删除失败。 叶子/扩展节点：分支节点：

示例：删除 Key “cat”

  • 找到 cat 对应的叶子节点。
  • 删除节点，导致父节点只有一个子节点： 分支节点变成叶子节点 扩展节点和叶子节点合并。

4. Update 操作   

  • Update(Key, Value)相当于Insert(如果Value不为空)。 
  •   Update(Key, NULL)相当于Delete

5. Commit操作(持久化，MPT)

Commit操作用于将MPT结构持久化到数据库，同时计算新的根哈希。

  • 递归遍历 MPT 树，计算每个节点的哈希： 若节点未修改，直接返回 缓存的哈希值。 若节点被修改，重新计算哈希：

  • RLP 编码当前节点数据

  • 计算 sha3(RLP(data)) 作为 新哈希

  • 子节点的哈希 递归计算。

  • 当前节点哈希计算：

  • 存入数据库：[节点哈希, RLP 编码]

  • 更新缓存，清除 dirty 标志。

六.MPT 在区块链中的应用

  • 快速计算数据集哈希    只有被修改的节点及其祖先节点需要重新计算哈希，提高效率。
    • 快速状态回滚  以太坊可能发生区块回滚，MPT 允许零延迟恢复历史状态。  原理：
  • 每个节点的哈希值是唯一且不可变的
  • 当状态变更时，只需替换变更节点的哈希索引，旧状态仍然可访问。
  • 无需删除旧数据，状态回滚时，只需切换到旧根哈希。

七.轻节点扩展与默克尔证明

  • 轻节点（Light Client）

    • 普通全节点存储完整区块数据。
    • 轻节点仅存区块头，不存交易数据。
    • 轻节点可以通过区块头的State Root验证区块状态。

  • 默克尔证明（Merkle Proof）

    • 轻节点可以请求全节点提供默克尔路径，用于验证数据是否存在。

    • 安全性： 

      •  全节点无法伪造默克尔路径 
      •    若全节点返回假数据，轻节点的哈希计算会与State Root不匹配，从而拒绝假数据。

    • 简单支付验证

    • 轻节点使用默克尔证明验证交易是否上链，而不需要下载完整区块数据。

八.布隆过滤器（Bloom Filter）

布隆过滤器（Bloom Filter）是一种空间效率极高的概率型数据结构，用于判断某个元素是否存在于集合中，但允许一定的误判率（False Positive）。它广泛应用于区块链、数据库、搜索引擎、反垃圾邮件检测等场景，特别适用于大规模数据集合的快速查找。

1. 布隆过滤器的基本特点

优点

  • 节省存储空间：相比哈希表（Hash Table），布隆过滤器不存储具体的 Key，而是仅存哈希标记，极大地减少了存储需求。
  • 查询速度快：基于位数组（Bit Array） 和多个哈希函数（Hash Functions），查询复杂度 O(k)（k 为哈希函数数量）。
  • 不会产生False Negative（假阴性）：如果布隆过滤器认为元素不存在，那它一定不存在。
  • 适用于大规模数据过滤：可以有效地减少数据库查询、网络请求、区块链存储开销。 缺点
  • 可能会产生False Positive（假阳性）：   
  • 误判率 ≠ 0，可能会认为不存在的元素实际上存在。   
  • 不能 100% 准确，但可以通过 调整参数（位数组大小和哈希函      数数量）降低误判率。
    • 无法删除元素（标准布隆过滤器）：     
    • 由于多个元素可能共享相同的位，所以无法确定是哪一个元素影响了该位。 
    • 解决方案：使用计数布隆过滤器（Counting Bloom Filter），用整数数组存储位的状态。

2. 布隆过滤器的工作原理

布隆过滤器使用位数组（Bit Array）和多个哈希函数（k 个）来标记元素是否可能存在。

2.1 数据结构

  • 位数组（Bit Array）：长度为m的二进制数组，初始时全部设为 0。
  • k 个独立的哈希函数：每个哈希函数H1, H2, ..., Hk对输入元素计算哈希值，并将结果映射到位数组的索引上。

2.2 插入操作（Insert）

插入一个元素 X 时：计算 X 的 k 个哈希值：

H1(X), H2(X), ..., Hk(X)
  • 将哈希值对应的 位数组位置设为 1。

2.3 查询操作（Check）

查询一个元素 Y 是否存在：计算 Y 的 k 个哈希值：

H1(Y), H2(Y), ..., Hk(Y)
  • 检查所有这些索引位置是否都为 1：
    • 如果全部是1：可能存在（但可能是误判）。
    • 如果至少有一个是0：一定不存在（不会误判）。

3. 具体示例

3.1.1 插入数据：

  • 假设 位数组长度 m = 10，哈希函数 k = 3。初始位数组：
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
  • 插入 "apple"
H1("apple") = 2H2("apple") = 4H3("apple") = 7

更新位数组：

[0, 0, 1, 0, 1, 0, 0, 1, 0, 0]

3.1.2 查询数据 查询 "orange"

  • H1("orange") = 3
  • H2("orange") = 5
  • H3("orange") = 8

检查位数组：

Bit 3 = 0, Bit 5 = 0, Bit 8 = 0

结论："orange" 一定不存在 ✅ 查询 "banana"

  • H1("banana") = 2
  • H2("banana") = 4
  • H3("banana") = 7

检查位数组：

Bit 2 = 1, Bit 4 = 1, Bit 7 = 1

结论："banana" 可能存在（误判） ❌

4.误判率计算

布隆过滤器的 误判率（False Positive Rate, FPR） 由以下公式计算：

P = (1 - e^(-kn/m))^k

其中：

  • m = 位数组大小（Bit Array Size）
  • n = 插入的元素数量（Number of Elements）
  • k = 哈希函数个数（Number of Hash Functions）
  • e = 自然对数的底（约 2.718）

降低误判率的方法

  • 增大 m（位数组大小）：空间大，则碰撞概率小。
  • 调整 k（哈希函数个数）：过少哈希函数导致碰撞率高，过多哈希函数导致位数组填充过快。
  • 使用动态布隆过滤器：多个布隆过滤器并行使用，避免误判过多。

5. 进阶优化

5.1 计数布隆过滤器（Counting Bloom Filter） 标准布隆过滤器无法删除元素，计数布隆过滤器用 整数数组 代替 二进制数组：

  • 插入时：对对应的 Counter +1
  • 删除时：对对应的 Counter -1

5.2分层布隆过滤器（Hierarchical Bloom Filter） 适用于大规模数据：

  • 采用多个层级的布隆过滤器，每层误判率不同
  • 例如比特币 SPV 轻节点 使用 分层布隆过滤器 过滤交易数据

6. 布隆过滤器的应用场景

  • 区块链
    • 以太坊使用布隆过滤器进行日志索引（Log Bloom Filter），加速事件查询。
    • 轻节点使用布隆过滤器过滤交易数据，仅下载与自己相关的交易。
    • 比特币 SPV（Simplified Payment Verification）
    • 以太坊日志索引
  • 数据库
    • Redis 提供布隆过滤器插件，用于快速判断数据是否存在，减少数据库查询压力。
    • Redis Bloom Filter
  • 搜索引擎
    • 网页爬虫：过滤已访问过的URL，防止重复抓取。
  • 反垃圾邮件
    • 维护垃圾邮件地址的布隆过滤器，快速判断邮件是否来自已知垃圾源。
    • 垃圾邮件检测

7. 总结

适用于 

  • 大规模数据过滤（如 区块链、数据库、搜索引擎） 
  • 低存储需求、高速查询的场景 需要注意 
  • 不能删除数据（标准版本） → 计数布隆过滤器解决 
  • 存在误判（False Positive） → 适用于 非精确查询

布隆过滤器以 高效存储和快速查询 在 区块链、分布式存储和大数据处理 领域有广泛应用

点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
Dapplink
Dapplink
0xBdcb...f214
首个模块化、可组合的Layer3协议。

Dapplink

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！