深入探讨Binius M3算术化，以Merkle树包含为例

介绍

任何零知识证明（ZKP）系统的核心在于算术化的概念，即将计算问题转化为可以在特定代数结构（如多项式或算术电路）中表达和验证的数学问题的过程。在 Binius 框架中，此算术化通过 多重多重集匹配 (M3) 系统进行管理，与更常用的算术化相比，它引入了重大的变化和改进。

虽然之前的帖子侧重于 Binius 使用的数学基础——例如 二元域 和 加法 FFT——但本文旨在探讨 Binius M3 系统的具体实现。为此，我们将深入研究一个特定的 工具 (Gadget)：Merkle 树。通过详细地研究这个例子，我们希望了解约束系统、表和通道如何在代码中表示和处理。

为了更普遍地了解我们在此详细解释的表和算术化技术为何有效，我们强烈建议阅读 Binius M3 文档。它非常清晰，并提供了玩具示例来帮助说明核心思想。

M3 的总体思路

与通常依赖于顺序主执行轨迹的传统算术化不同，M3 的特点是不需要主轨迹或表是顺序的。在 M3 中，表仅仅是声明性的实例，专门为证明的目的而设计。证明者用与计算相关的数据填充这些表，这些表充当与一个关键组件通道 (Channels) 交互的来源。

在 M3 中，表和通道是构建和验证复杂计算的基本支柱。表 (Tables) 是表示和结构化计算数据的主要手段，充当列的集合，其中每一行代表操作的步骤或实例。例如，在 Merkle 树的上下文中，某些表将具有父节点和子节点的数据。

作为表的补充，通道 (Channels) 充当 M3 约束系统中的通信管道。它们促进不同表之间或表与外部世界（例如公共输入和输出）之间的数据流动。表将数据 推入 (Push) 或从通道中 拉取 (Pull) 数据。这种机制对于连接复杂计算的各个部分至关重要，确保正确维护和验证数据依赖性。为了验证证明的有效性，验证者只需检查所有通道是否 平衡 (Balanced)，这意味着推入通道的数据与从中拉取的数据相匹配。

虽然 M3 也像以前的方案一样依赖于多项式约束表，但它通过仅使用这些表来支持通道平衡，而不是作为构建全局执行跟踪的工具，从而背离了传统方法。

在本文中，我们将探讨 Binius Merkle 树约束系统中的表和通道的具体示例，说明它们如何用于构建 Merkle 树包含的可验证证明。为了看到所有这些理论的实际应用，Merkle 树示例将设置包装在一个帮助器中：MerkleTreeCS。调用 MerkleTreeCS::new 会设置五个表，打开三个通道，并返回一个准备用路径数据填充的约束系统。在处理完管道之后，我们现在可以看看每个表和通道的作用了。

MerkleTreeCS

MerkleTreeCS（Merkle 树约束系统）由 5 个表和 3 个通道组成，它们协同工作以确保 Merkle 路径验证的正确性。

表

• merkle_path_table_left: 一个 NodesTable 类型的表，用于处理 Merkle 路径，其中只有左子节点必须从通道中拉取。稍后我们将详细了解这意味着什么。
• merkle_path_table_right: 一个 NodesTable 类型的表，用于处理只拉取右子节点的情况。
• merkle_path_table_both: 一个 NodesTable 类型的表，用于处理同时拉取左右子节点的情况。
• root_table: 一个 RootTable 类型的表，用于协调 Merkle 路径的最终值与预期的根。
• incr_table: 一个 IncrLookup 类型的表。用于递增操作的查找表，以验证父节点和子节点之间的深度关系。

通道：

• nodes_channel - 管理 Merkle 路径中的中间节点（格式：[Root ID, Digest, Depth, Index]）
• roots_channel - 处理根验证（格式：[Root ID, Digest]）
• lookup_channel - 协调递增操作以验证子节点深度是否为父节点深度加一。

初始化

MerkleTreeCS::new() 方法构建整个约束系统。此方法的主要目标是将表和通道添加到 cs（约束系统）并创建 MerkleTreeCS。

pub fn new(cs: &mut ConstraintSystem) -> Self {
    let nodes_channel = cs.add_channel("merkle_tree_nodes");
    let roots_channel = cs.add_channel("merkle_tree_roots");
    let lookup_channel = cs.add_channel("incr_lookup");
    let permutation_channel = cs.add_channel("permutation");  // ← NEW CHANNEL!

    // Create the three Merkle path tables
    let merkle_path_table_left =
        NodesTable::new(cs, MerklePathPullChild::Left, nodes_channel, lookup_channel);
    let merkle_path_table_right =
        NodesTable::new(cs, MerklePathPullChild::Right, nodes_channel, lookup_channel);
    let merkle_path_table_both =
        NodesTable::new(cs, MerklePathPullChild::Both, nodes_channel, lookup_channel);

    let root_table = RootTable::new(cs, nodes_channel, roots_channel);

    // Create the increment lookup table with the new permutation channel
    let mut table = cs.add_table("incr_lookup_table");
    let incr_table = IncrLookup::new(&mut table, lookup_channel, permutation_channel, 20);

    Self { /* ... */ }
}

可以看出，还有一个之前没有提到的额外通道：

permutation_channel 是专门为 IncrLookup 表引入的一个新通道。此通道在查找表验证过程中起着至关重要的作用。它确保 IncrLookup 中的两列是彼此的排列。这些列称为 entries_ordered 和 entries_sorted，我们稍后将详细检查它们。

逐步示例

我们认为，理解约束系统是如何构建的以及表是如何创建的，最好的方法是看一个例子。为此，我们将使用 Binius 在 merkle_tree.rs 中提供的示例，我们可以在其中构建树、一些路径、约束系统以及验证这些路径的证明。

该文件以一些我们将要调整的参数开始。为简单起见，我们想要创建一个包含 8 个叶子的树，并证明其中两个叶子是树的一部分。换句话说，对于 log_leaves，我们将采用 default_value_t = 3（因为我们想要一个 8 个叶子的树），对于 log_paths，采用 default_value_t = 1（因为我们想证明两个路径），对于 log_inv_rate，采用 default_value_t = 1。

struct Args {
    /// The number of leaves in the merkle tree.
    /// By default 8 leaves.
    #[arg(long, default_value_t = 3, value_parser = value_parser!(u32).range(1..))]
    log_leaves: u32,

    /// The number of Merkle paths to verify.
    /// By default 2 paths.
    #[arg(short,long, default_value_t = 1, value_parser = value_parser!(u32).range(1..))]
    log_paths: u32,

    /// The negative binary logarithm of the Reed–Solomon code rate.
    #[arg(long, default_value_t = 1, value_parser = value_parser!(u32).range(1..))]
    log_inv_rate: u32,
}

构建树和路径

现在我们有了这些参数，如果你跟随 main() 函数，你就会看到在那里构建了树和 Merkle 路径。让我们在这部分代码中添加一些打印，以查看它们的值。

/* ... */

let mut rng = StdRng::seed_from_u64(0);
// Create a Merkle Tree with 8 leaves
let leaves = (0..1 << args.log_leaves)
    .map(|_| rng.r#gen::<[u8; 32]>())
    .collect::<Vec<_>>();

let tree = MerkleTree::new(&leaves);

let roots: [u8; 32] = tree.root();

println!("--------- Merkle tree data -------");
println!("Leaves: {:?}", leaves);
println!("Root: {:?}", roots);

let paths = (0..1 << args.log_paths)
    .map(|_| {
        let index = rng.gen_range(0..1 << args.log_leaves);
        println!("------- Path data -------");
        println!("Proving leaf index: {:?}", index);
        println!("Proving leaf: {:?}", leaves[index]);
        println!("Merkle tree path: {:?}", tree.merkle_path(index));

        MerklePath {
            root_id: 0,
            index,
            leaf: leaves[index],
            nodes: tree.merkle_path(index),
        }
    })
    .collect::<Vec<_>>();

/* ... */

这将首先打印八个叶子和根（每一个都是一个 32 字节的数组）：

--------- Merkle tree data -------
Leaves: [\
    [127, 178, 123, 148, 22, 2, 208, 29, 17, 84, 34, 17, 19, 79, 199, 26, 172, 174, 84, 227, 126, 125, 0, 123, 187, 123, 85, 239, 240, 98, 162, 132],\
    [154, 99, 40, 60, 186, 240, 253, 188, 235, 31, 100, 121, 177, 151, 243, 168, 141, 208, 216, 9, 47, 231, 42, 124, 86, 40, 21, 56, 115, 139, 7, 226],\
    [114, 238, 165, 17, 148, 16, 151, 58, 227, 40, 173, 146, 145, 98, 104, 18, 142, 219, 71, 16, 110, 26, 214, 168, 195, 213, 69, 132, 155, 138, 184, 27],\
    [16, 24, 93, 38, 2, 59, 54, 16, 206, 183, 217, 245, 125, 73, 210, 179, 135, 99, 161, 43, 43, 189, 250, 147, 39, 90, 255, 24, 42, 251, 149, 220],\
    [118, 35, 234, 226, 120, 82, 64, 185, 61, 18, 177, 106, 102, 216, 22, 16, 124, 220, 140, 137, 199, 16, 143, 255, 32, 149, 225, 141, 223, 239, 137, 134],\
    [177, 24, 234, 85, 97, 98, 77, 166, 204, 83, 123, 174, 213, 110, 96, 47, 147, 140, 128, 78, 39, 248, 49, 150, 97, 12, 136, 40, 199, 35, 247, 152],\
    [80, 79, 178, 164, 68, 97, 204, 11, 235, 179, 37, 40, 14, 217, 19, 10, 89, 187, 219, 49, 28, 1, 253, 115, 73, 9, 161, 31, 158, 72, 102, 40],\
    [180, 59, 54, 61, 129, 174, 139, 104, 153, 70, 236, 229, 198, 130, 205, 89, 138, 101, 234, 191, 246, 58, 53, 114, 223, 228, 95, 181, 173, 229, 139, 220]\
]
Root: [193, 178, 67, 64, 61, 105, 200, 119, 129, 200, 250, 91, 108, 49, 178, 161, 234, 142, 150, 145, 206, 128, 43, 153, 216, 191, 196, 183, 198, 179, 118, 122]

然后是第一个 Merkle 路径：

------- Path data -------
Proving leaf index: 3
Proving leaf: [16, 24, 93, 38, 2, 59, 54, 16, 206, 183, 217, 245, 125, 73, 210, 179, 135, 99, 161, 43, 43, 189, 250, 147, 39, 90, 255, 24, 42, 251, 149, 220]
Merkle tree path: [\
    [114, 238, 165, 17, 148, 16, 151, 58, 227, 40, 173, 146, 145, 98, 104, 18, 142, 219, 71, 16, 110, 26, 214, 168, 195, 213, 69, 132, 155, 138, 184, 27],\
    [246, 247, 101, 36, 57, 192, 24, 48, 162, 208, 160, 30, 187, 154, 180, 176, 208, 104, 135, 216, 175, 8, 0, 249, 96, 50, 194, 72, 102, 219, 184, 27],\
    [70, 219, 30, 17, 251, 21, 8, 37, 23, 248, 120, 106, 49, 210, 42, 247, 15, 227, 231, 151, 101, 7, 187, 203, 29, 109, 186, 223, 43, 126, 183, 173]\
]

最后，是第二个 Merkle 路径：

------- Path data -------
Proving leaf index: 4
Proving leaf: [118, 35, 234, 226, 120, 82, 64, 185, 61, 18, 177, 106, 102, 216, 22, 16, 124, 220, 140, 137, 199, 16, 143, 255, 32, 149, 225, 141, 223, 239, 137, 134]
Merkle tree path: [\
    [177, 24, 234, 85, 97, 98, 77, 166, 204, 83, 123, 174, 213, 110, 96, 47, 147, 140, 128, 78, 39, 248, 49, 150, 97, 12, 136, 40, 199, 35, 247, 152],\
    [44, 37, 79, 124, 156, 84, 213, 102, 239, 101, 1, 89, 211, 73, 117, 58, 143, 41, 102, 47, 67, 32, 248, 100, 29, 138, 44, 204, 232, 177, 216, 54],\
    [124, 166, 97, 100, 173, 242, 98, 95, 141, 158, 147, 144, 202, 239, 150, 192, 0, 99, 9, 138, 61, 19, 65, 163, 160, 4, 227, 66, 233, 115, 199, 3]\
]

因此，我们的 Merkle 树应该看起来像下面这样。为了使图形更具可读性，我们只编写了每个节点的第一个字节，即使我们应该编写所有 32 个字节。第一条路径以绿色显示，第二条路径以蓝色显示。你可能想知道我们如何知道中间节点“181”和“67”的内容，因为它们既不是叶子、根，也不是 Merkle 路径的一部分。我们是从稍后将进行的打印中获得该信息的。

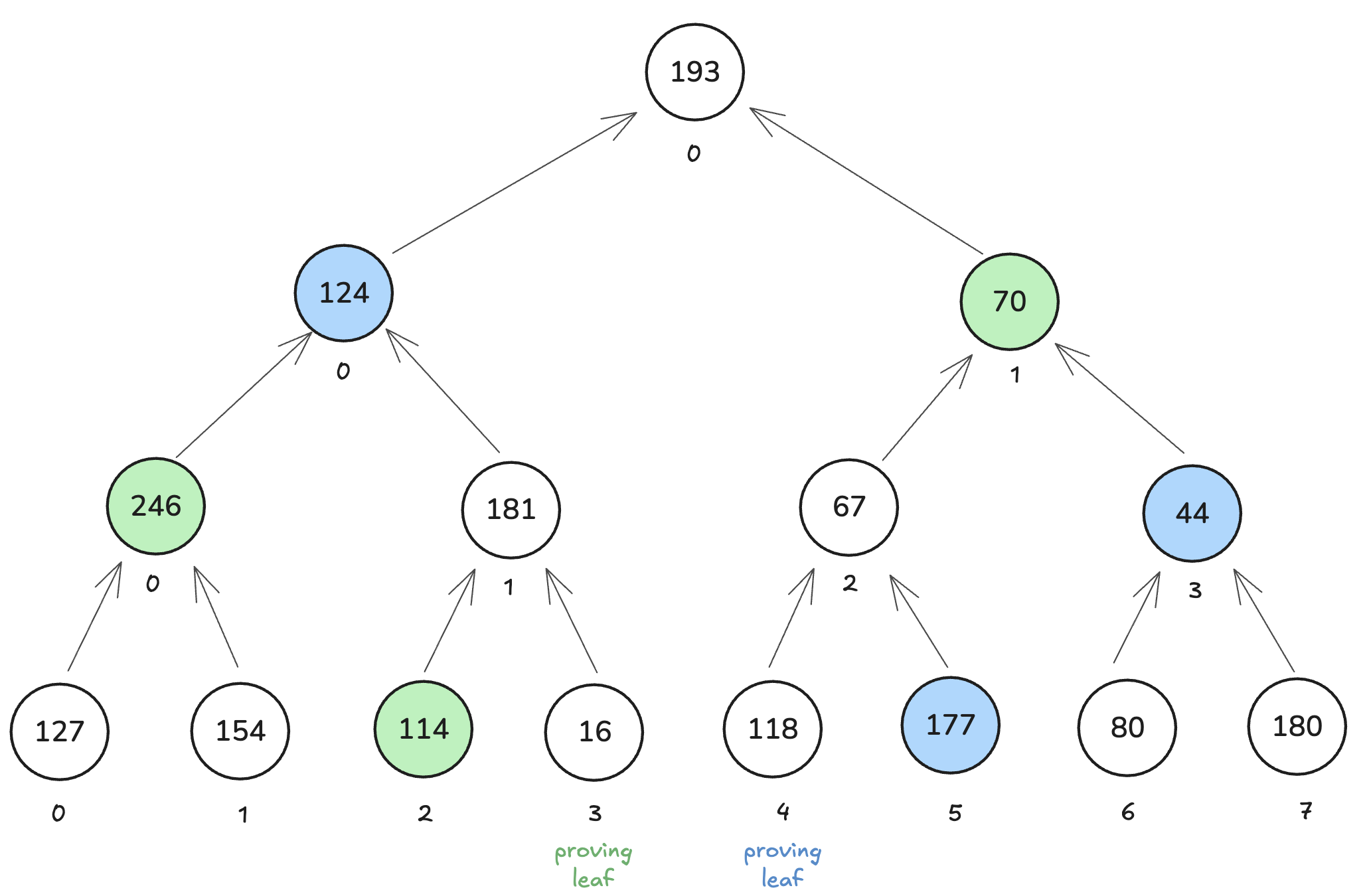
在本帖的其余部分，我们将解释 MerkleTreeCS 中使用的三种类型的表：NodesTable、RootTable 和 IncrLookup。

它们是做什么用的？如何填充它们？它们如何与不同的通道交互？我们将使用我们刚刚构建的树作为示例来回答这些问题。

NodesTable

目的

此表类型旨在处理父节点和子节点之间的关系。表中的每一行对应一个 MerklePathEvent，用于捕获三个相关节点：两个子节点（左和右）及其父节点之间的交互。

在证明 Merkle 树路径时，通过遍历每个路径并为遇到的每个父子三人组创建一行来填充表。这种系统方法确保所有必要的节点关系都得到正确编码，并且可以通过约束系统进行验证。

内容和列

NodesTable 包含一组可以分为三个主要组的列：

1. MerklePathEvent 数据

这些列存储有关每个节点关系的基本信息：

• root_id：标识三个节点属于哪个 Merkle 树。
• left_columns、right_columns：存储左子节点和右子节点的摘要值。
• parent_depth、child_depth：指示父节点和子节点所在的树级别。这些级别（或深度）从顶部（根）的 0 开始，一直到 log2(leaves.len())log2⁡(leaves.len())，以叶子结束。
• parent_index、left_index、right_index_packed：存储节点的定位索引。
• _pull_child：指定需要从通道中拉取哪个子节点。
  2. Groestl-256 哈希计算

这些列处理加密哈希运算：

• state_out_shifted：包含为 Groestl-256 置换组织的左子节点和右子节点的串联字节。
• permutation_output_columns：存储 Groestl-256 输出转换后的字节。
• permutation：Groestl-256 置换工具。

注意：这是工具强大功能的一个清晰示例。从某种意义上说，负责验证 Merkle 路径的工具将检查哈希函数有效性的任务委托给另一个工具（本文未详细介绍，但它以类似的方式运行）。这种模块化方法允许我们以干净且可扩展的方式构建更复杂程序的证明。

3. 深度约束

increment：一个用于确保子节点深度恰好比父节点深度大一的工具。

初始化

NodesTable 通过其 new() 方法创建。此初始化过程涉及：

• 使用 cs.add_table() 将表添加到约束系统。

• 使用 table.add_committed() 或 table.add_committed_multiple() 将提交列添加到表中。

• 使用 table.add_packed()、table.add_shifted() 和 table.add_computed() 将虚拟列添加到表中。在 Binius 文档 中，你可以看到对提交列和虚拟列之间差异的解释。

注意：这在 M3 中尤其相关，因为它代表了与其他证明系统相比的关键差异之一。虚拟列通过允许证明者仅提交到减少数量的表格（提交列）来发挥基本作用，同时避免了提交到虚拟列的需要。之所以可以这样做，是因为从提交列重建虚拟列所需的所有信息都完全编码在约束系统中。

• 建立零约束以确保左子节点和右子节点的串联等于父哈希的输入。这是使用 table.assert_zero() 实现的。

for i in 0..8 {
    table.assert_zero(
        format!("state_in_assert[{i}]"),
        state_in_packed[i]
            - upcast_col(left_packed[i])
            - upcast_col(right_packed[i]) * B64::from(1 << 32),
    );
}

• 设置刷新规则，通过 nodes_channel.push() 和 nodes_channel.pull() 定义表如何与 NodesChannel 交互。

通道交互

让我们更详细地解释一下表初始化中提到的最后一点。NodesTable 通过以下推入/拉取规则与 NodesChannel 交互：推入父节点，拉取子节点。

• 推入：应将父节点信息（根 ID、内容、深度和索引）推入通道。
• 拉取：根据 pull_child 输入，从通道中拉取左子节点、右子节点或两个子节点。对于每个路径，根据路径路线，只能拉取一个子节点，左或右。但是，如果有一个父子三人组 Merkle 事件在不同的路径中使用，则一次拉取左侧，一次拉取右侧，然后拉取两个子节点。

表格填充

结构体 NodesTable 实现了 TableFiller trait，其核心填充逻辑在 fill() 函数中。对于每个 MerklePathEvent，该函数：

• 提取节点关系数据（父节点、左子节点、右子节点）
• 计算派生值，如子节点索引和深度递增。
• 使用串联的子节点数据填充置换状态。
• 使用适当的值填充所有表格列。

此填充过程将跟踪数据转换为生成和验证证明所需的约束系统表示。

我们的示例

为了理解 MerklePathEvent 是什么以及如何填充这些表格，让我们看一个例子。

在 merkle_tree.rs 示例的 main() 函数中，一旦我们有了树和路径，就会生成跟踪，然后使用函数 fill_tables() 填充表格。在这里，我们可以添加更多打印，以查看所有这些数据的外观。

pub fn fill_tables(
    &self,
    trace: &MerkleTreeTrace,
    cs: &ConstraintSystem,
    witness: &mut WitnessIndex,
) -> anyhow::Result<()> {
    // Filter the MerklePathEvents into three iterators based on the pull child type.
    let left_events = trace
        .nodes
        .iter()
        .copied()
        .filter(|event| event.flush_left && !event.flush_right)
        .collect::<Vec<_>>();
    let right_events = trace
        .nodes
        .iter()
        .copied()
        .filter(|event| !event.flush_left && event.flush_right)
        .collect::<Vec<_>>();
    let both_events = trace
        .nodes
        .iter()
        .copied()
        .filter(|event| event.flush_left && event.flush_right)
        .collect::<Vec<_>>();

    println!("------- Merkle Path Events -------");
    println!("Left events: {:?}", &left_events);
    println!("Right events: {:?}", &right_events);
    println!("Both events: {:?}", &both_events);

    // Fill the nodes tables based on the filtered events.
    witness.fill_table_parallel(&self.merkle_path_table_left, &left_events)?;
    witness.fill_table_parallel(&self.merkle_path_table_right, &right_events)?;
    witness.fill_table_parallel(&self.merkle_path_table_both, &both_events)?;

    /*...*/
}

这将首先打印左侧事件：

Left events: [\
    MerklePathEvent {\
        root_id: 0,\
        left: [67, 45, 38, 237, 191, 26, 225, 172, 10, 94, 207, 176, 214, 146, 204, 230, 180, 241, 18, 217, 51, 18, 215, 92, 201, 50, 136, 22, 3, 172, 197, 55],\
        right: [44, 37, 79, 124, 156, 84, 213, 102, 239, 101, 1, 89, 211, 73, 117, 58, 143, 41, 102, 47, 67, 32, 248, 100, 29, 138, 44, 204, 232, 177, 216, 54],\
        parent: [70, 219, 30, 17, 251, 21, 8, 37, 23, 248, 120, 106, 49, 210, 42, 247, 15, 227, 231, 151, 101, 7, 187, 203, 29, 109, 186, 223, 43, 126, 183, 173],\
        parent_depth: 1,\
        parent_index: 1,\
        flush_left: true,\
        flush_right: false\
    },\
    MerklePathEvent {\
        root_id: 0,\
        left: [118, 35, 234, 226, 120, 82, 64, 185, 61, 18, 177, 106, 102, 216, 22, 16, 124, 220, 140, 137, 199, 16, 143, 255, 32, 149, 225, 141, 223, 239, 137, 134],\
        right: [177, 24, 234, 85, 97, 98, 77, 166, 204, 83, 123, 174, 213, 110, 96, 47, 147, 140, 128, 78, 39, 248, 49, 150, 97, 12, 136, 40, 199, 35, 247, 152],\
        parent: [67, 45, 38, 237, 191, 26, 225, 172, 10, 94, 207, 176, 214, 146, 204, 230, 180, 241, 18, 217, 51, 18, 215, 92, 201, 50, 136, 22, 3, 172, 197, 55],\
        parent_depth: 2,\
        parent_index: 2,\
        flush_left: true,\
        flush_right: false\
    }\
]

这个事件是左侧事件，因为必须从通道中拉出的节点是左侧子节点“67”：

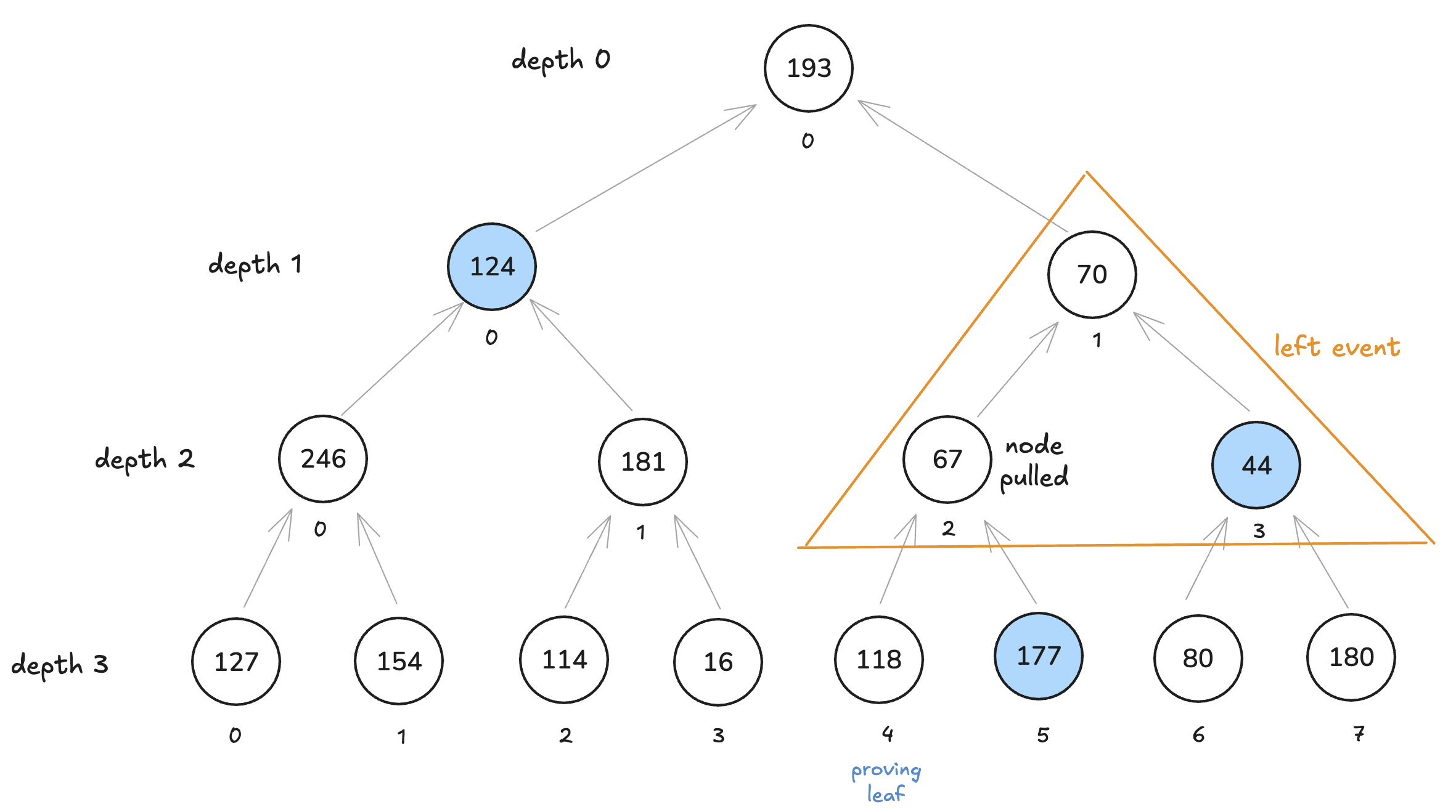
第二个事件也是如此。在这里，必须拉取的节点是左侧## RootTable

目的

RootTable 是 Binius Merkle Tree 约束系统中的一个表，负责将 Merkle 路径的最终值与声明的 Merkle 根进行协调。当 NodesTable 验证路径中的步骤时，RootTable 提供了最终的密码学保证，即这些路径通向正确的、预先提交的 Merkle 根。

内容

pub struct RootTable {
    pub id: TableId,
    pub root_id: Col<B8>,
    pub digest: [Col<B32>; 8]
}

该表包含我们正在分析的所有树的根节点的数据（Id 和摘要，或内容），因为我们可以证明不同树的不同路径。

初始化

RootTable 的初始化通过其方法 new() 完成：

impl RootTable {
    pub fn new(
        cs: &mut ConstraintSystem,
        nodes_channel: ChannelId,
        roots_channel: ChannelId,
    ) -> Self {

        /*...*/
    }
}

此函数：

1. 向 cs 添加一个表：

let mut table = cs.add_table("merkle_tree_roots");

2. 在该表中定义列（committed 和/或 virtual）：

let root_id = table.add_committed("root_id");
let digest = table.add_committed_multiple("digest");

let zero = table.add_constant("zero", [B32::ZERO]);

3. 添加与该表及其通道（nodes_channel 和 roots_channel）关联的 flushing 规则。

table.pull(roots_channel_id, to_root_flush(root_id_upcasted, digest));
let mut nodes_channel = NodesChannel::new(&mut table, nodes_channel_id);
nodes_channel.pull(root_id_upcasted, digest, zero, zero);

Flushing 规则

RootTable 主要与 nodes_channel 和 roots_channel 交互以执行其协调。 它将从两个通道 pull 数据以验证一致性。

• nodes_channel：此通道携带有关 Merkle 路径的所有中间节点和最终节点的信息。 RootTable 将从此通道 pull 路径的最终节点的摘要。
• roots_channel：此通道包含正在验证的实际 Merkle 根。 RootTable 将 pull 这些值，以确保路径的端点与有效的根之一匹配。

flushing 规则将确保必要的数据（最终路径节点摘要和声明的根摘要）可用于 RootTable 进行其内部一致性检查。 这种比较构成了根验证的零知识约束的核心，确保 Merkle 路径确实通向声明的根。

IncrLookup

目的

除了 NodesTable 和 RootTable 之外，Binius Merkle Tree 约束系统还使用 IncrLookup。 这是一种专用的 gadget，旨在高效地验证带有进位位的 8 位增量操作。 IncrLookup 允许证明者简单地证明执行的每个操作都存在于所有有效增量结果的预定义表中，而不是为每个增量操作实例编写复杂的算术约束。 这显著降低了计算成本和证明大小。

在 Merkle 树包含证明的特定上下文中，IncrLookup 用于确保在每个 MerklePathEvent 中，子节点的深度恰好比父节点的深度大 1。

内容

IncrLookup 只有两列 entries_ordered 和 entries_sorted。 两列具有完全相同的值，但排序方式不同。 我们稍后将看到如何填充这些列。

struct IncrLookup 还有一个字段 lookup_producer。LookupProducer 是负责创建查找表的 gadget。

初始化

当设置 MerkleTreeCS 时，会创建一个 IncrLookup 实例（参见此处），通过其方法 new()，它执行以下操作：

1. 修复列的大小：

table.require_fixed_size(IncrIndexedLookup.log_size());

请注意，IncrIndexedLookup.log_size() 是 29=51229=512，如你所见此处。 这是因为列的每个索引 i∈0,…,511i∈0,…,511 都将表示某个特定输入的递增。 ii 的 8 个最低有效位告诉我们输入，最高有效位告诉我们进位。

2. 将 entries_ordered 和 entries_sorted 列添加到表中。

3. 为约束系统的 permutation_channel 添加 flushing 规则，以确保一列是另一列的排列：

// 使用 flush 检查 entries_sorted 是否是 entries_ordered 的排列。
table.push(permutation_chan, [entries_ordered]);
table.pull(permutation_chan, [entries_sorted]);

4. 配置一个 LookupProducer 来管理如何查询条目并处理它们的多重性（在证明期间每个特定增量操作发生的次数）。

表填充

与其他表一样，MerkleTreeCS 的 incr_table 也在函数 fill_tables() 中填充，特别是在这部分：

let lookup_counts = tally(cs, witness, &[], self.lookup_channel, &IncrIndexedLookup)?;

// 使用排序后的计数填充查找表
let sorted_counts = lookup_counts
    .into_iter()
    .enumerate()
    .sorted_by_key(|(_, count)| Reverse(*count))
    .collect::<Vec<_>>();
witness.fill_table_parallel(&self.incr_table, &sorted_counts)?;

让我们详细分析一下这段代码。 为此，我们必须了解变量 lookup_counts 是什么以及函数 tally() 的作用。

Lookup Counts

lookup_counts 是一个包含 512 个整数元素的向量。 该向量是函数 tally() 的结果。 正如其文档所解释的那样，此函数“确定索引查找表中每个条目的读取计数”。 它迭代约束系统的每个表，查找特定的 flushing 规则：对输入通道的 pull 操作。 在我们的例子中，输入通道被称为 lookup_channel。 每当它找到此 flushing 规则时，它会在特定索引处将 1 添加到结果向量（这取决于要 pull 的值）。

为了理解如何选择此索引，让我们添加一些打印并查看我们的示例中发生了什么。

pub fn tally<P>(
    cs: &ConstraintSystem<B128>,
    // TODO: This doesn't actually need mutable access. But must of the WitnessIndex methods only
    // allow mutable access.
    witness: &mut WitnessIndex<P>,
    boundaries: &[Boundary<B128>],
    chan: ChannelId,
    indexed_lookup: &impl IndexedLookup<B128>,
) -> Result<Vec<u32>, Error>
where
    P: PackedField<Scalar = B128>
        + PackedExtension<B1>
        + PackedExtension<B8>
        + PackedExtension<B16>
        + PackedExtension<B32>
        + PackedExtension<B64>
        + PackedExtension<B128>,
{
    println!("------- Look up counts for channel: {chan} -------");
    let mut counts = vec![0; 1 << indexed_lookup.log_size()]; // 2^{8+1}

    // Tally counts from the tables
    for table in &cs.tables {
        // In merkle tree example, NodesTable and RootTable
        if let Some(table_index) = witness.get_table(table.id()) {
            println!("--- Processing table: {} (ID: {}) ---", table.name, table.id());
            for partition in table.partitions.values() {
                for flush in &partition.flushes {
                    if flush.channel_id == chan && flush.direction == FlushDirection::Pull {
                        // In the merkle tree example, this occurs in every NodesTable pull from the
                        // lookup_channel.
                        println!(
                            "Found matching flush: The table has a Pull operation on channel {}",
                            chan
                        );

                        let table_size = table_index.size();
                        // TODO: This should be parallelized, which is pretty tricky.
                        let segment = table_index.full_segment();
                        let cols = flush
                            .columns
                            .iter()
                            .map(|&col_index| segment.get_dyn(col_index))
                            .collect::<Result<Vec<_>, _>>()?;

                        if !flush.selectors.is_empty() {
                            // TODO: check flush selectors
                            todo!("tally does not support selected table reads yet");
                        }

                        let mut elems = vec![B128::ZERO; cols.len()];
                        // It's important that this is only the unpacked table size(rows * values
                        // per row in the partition), not the full segment size. The entries
                        // after the table size are not flushed.
                        for i in 0..table_size * partition.values_per_row {
                            for (elem, col) in iter::zip(&mut elems, &cols) {
                                *elem = col.get(i);
                            }
                            let index = indexed_lookup.entry_to_index(&elems);
                            println!("Index {index} corresponds to element: {:?}", elems);
                            counts[index] += 1;
                        }
                    }
                }
            }
        }
    }

这首先应该打印以下内容：

------- Look up counts for channel: 2 -------
--- Processing table: merkle_tree_nodes_left (ID: 0) ---
Found matching flush: The table has a Pull operation on channel 2
Index 258 corresponds to element: [BinaryField128b(0x00000000000000000000000000010302)]
Index 257 corresponds to element: [BinaryField128b(0x00000000000000000000000000010201)]

这告诉我们以下信息：我们正在寻找通道 2（lookup_channel）上的 pull out，并且我们首先分析具有 左事件 的 NodesTable。 在该表中，它遇到了两个来自通道的 pull out：

1. 第一个 pull out 是

BinaryField128b(0x00000000000000000000000000010302)。 要了解此二进制字段元素代表什么，请按照以下步骤操作：

• 将其十六进制值转换为二进制扩展：

  0x10302=000100000011000000100x10302=00010000001100000010

• 取 8 个最低有效位。 结果数字称为 输入：0000001000000010。
• 取位置 16 处的位（从 LSB 到 MSB 并从 0 开始）。 结果数字称为 carry in：11

• 以以下方式连接它们：carry in || 输入。 这导致

  100000010.100000010.

• 结果是索引的二进制扩展：

  100000010=258.100000010=258.

现在，所有这些与我们的 Merkle 树有什么关系？ 好吧，这个索引 258258 在以下事件中代表父节点和子节点的深度：

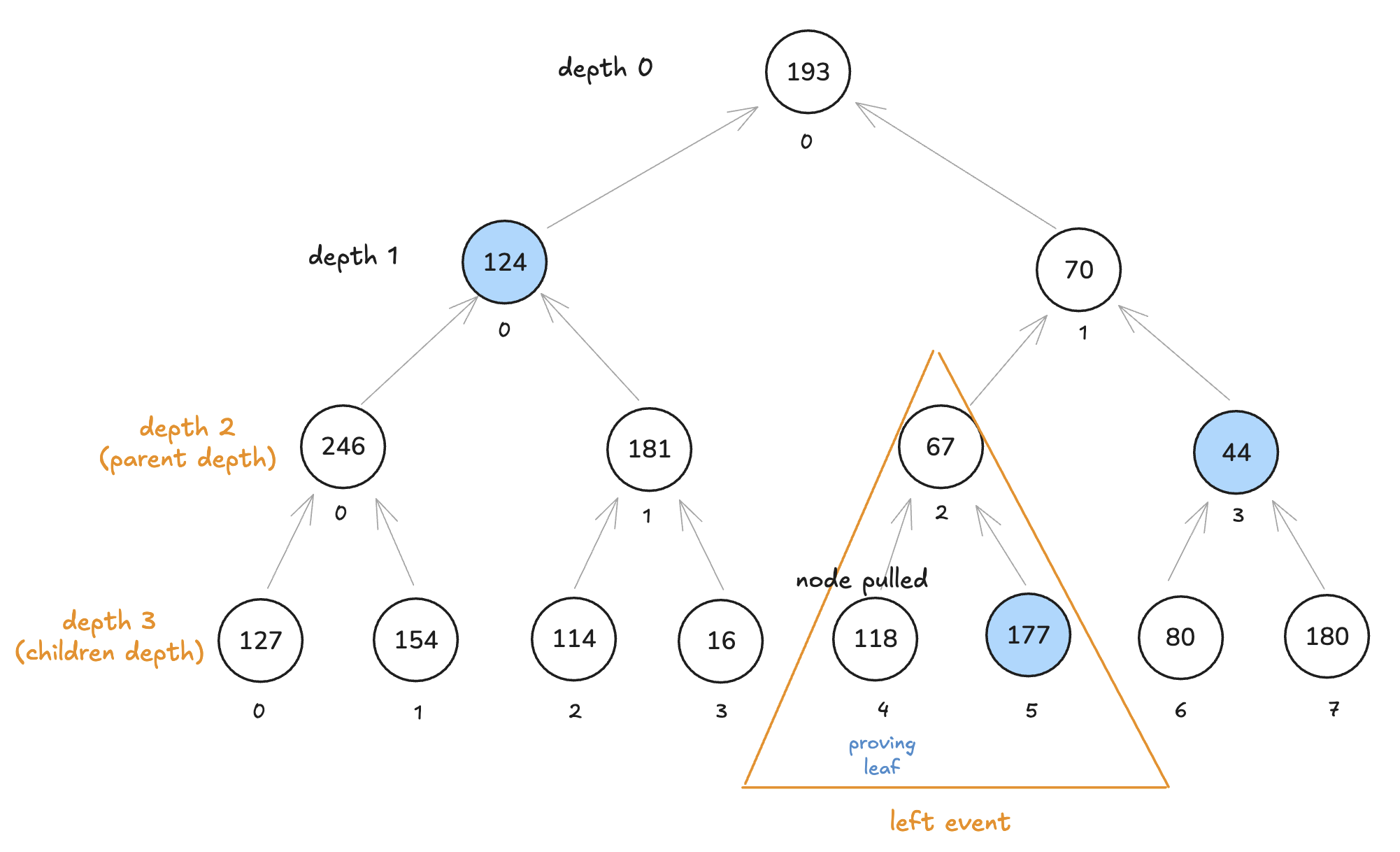
由于父节点的深度为 2，因此输入将为 0000001000000010。 并且由于子节点深度是父节点深度加 1，因此进位是 11。你可以在每个 NodesTable 的初始化中更好地看到这一点（此处），在此特定部分：

let parent_depth = table.add_committed("parent_depth");

let one = table.add_constant("one", [B1::ONE]);

let increment = Incr::new(&mut table, lookup_chan, parent_depth, one);
let child_depth = increment.output;

这里，输入 是 parent_depth，carry_in 是 one。

2. 第二个 pull out 是 BinaryField128b(0x00000000000000000000000000010201)。 让我们做与上面相同的事情：

   • 转换为二进制：0x10201=000100000010000000010x10201=00010000001000000001
   • 然后，input = 00000001。 这意味着它代表深度为 1 的父节点的事件。
   • carry_in = 1 因为子节点深度是父节点深度加 1。

   • 连接以获取索引：100000001=257100000001=257.

     此索引对应于以下事件：

     

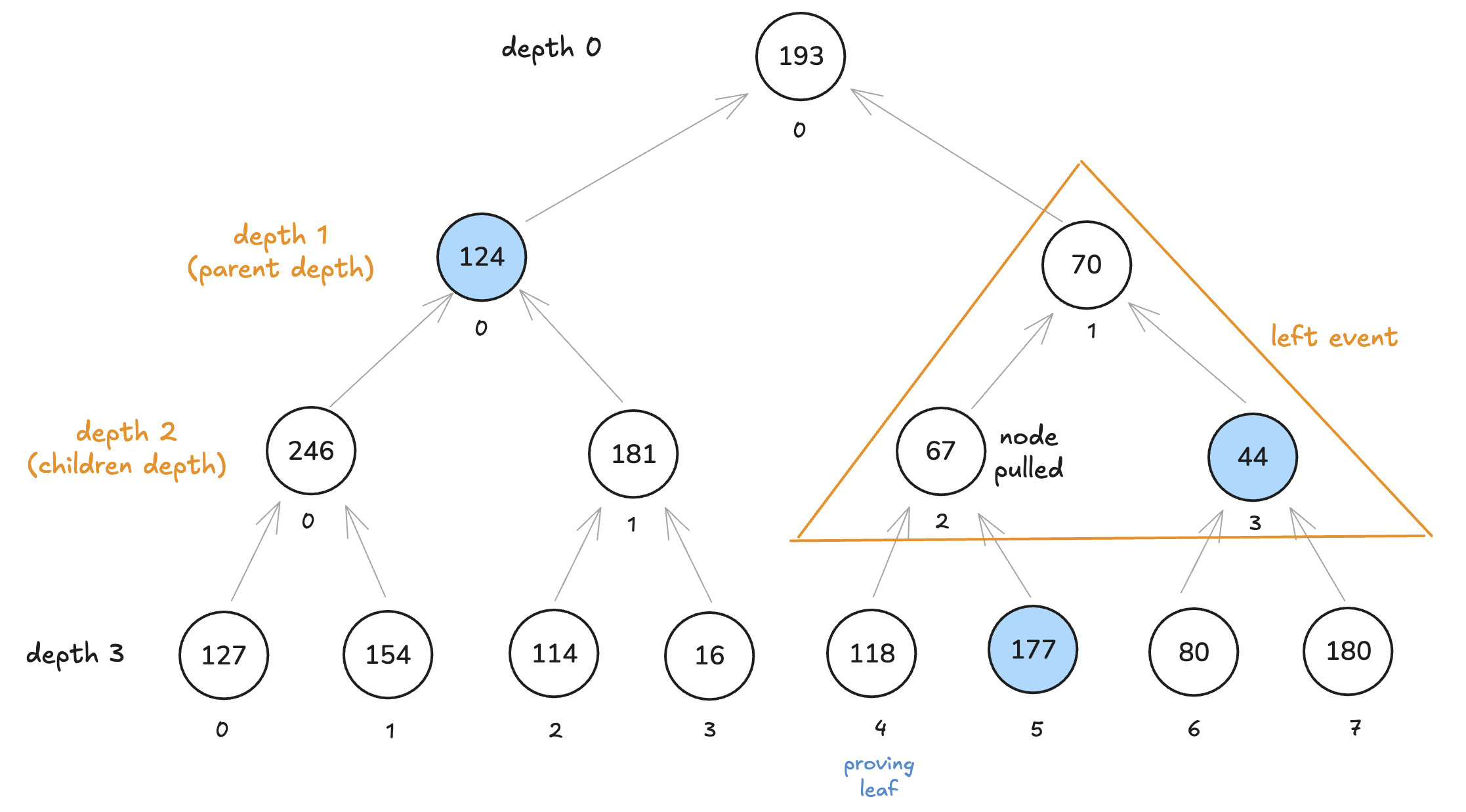
现在，让我们看看函数 tally() 还打印了什么。 你还应该看到这个：

--- Processing table: merkle_tree_nodes_right (ID: 1) ---
Found matching flush: The table has a Pull operation on channel 2
Index 257 corresponds to element: [BinaryField128b(0x00000000000000000000000000010201)]
Index 258 corresponds to element: [BinaryField128b(0x00000000000000000000000000010302)]

请注意，我们这里有与以前相同的索引。 这是因为右侧事件与左侧事件具有相同的父节点深度：

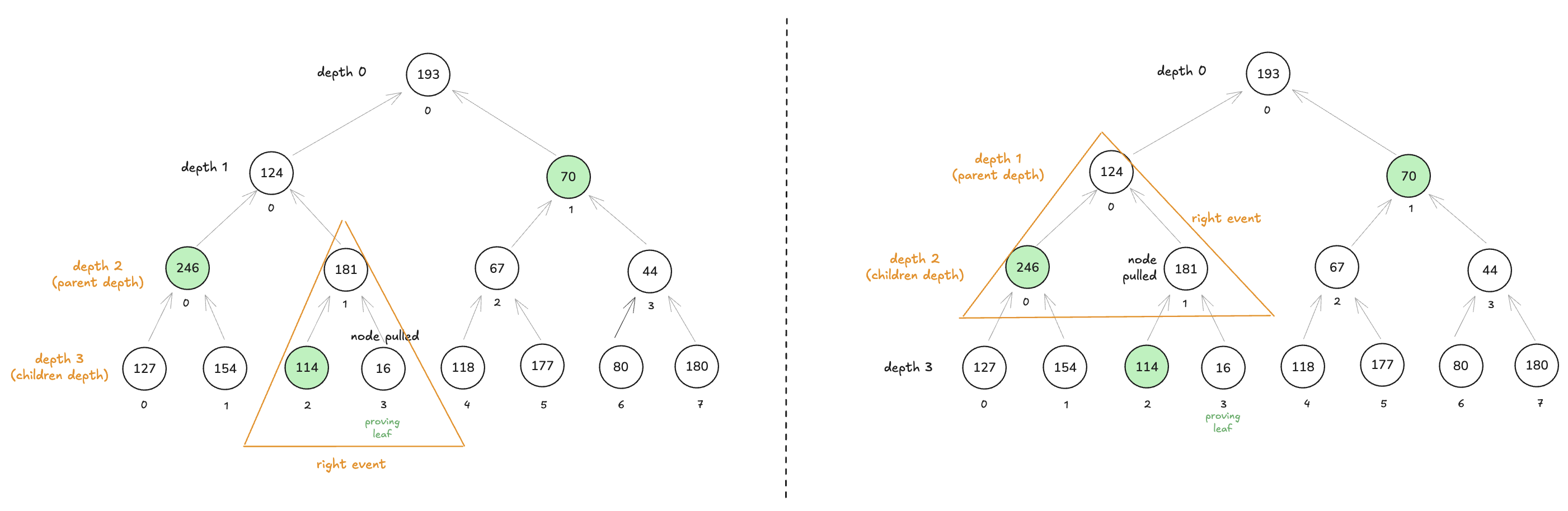
之后，你应该在终端中看到以下内容：

--- Processing table: merkle_tree_nodes_both (ID: 2) ---
Found matching flush: The table has a Pull operation on channel 2
Index 256 corresponds to element: [BinaryField128b(0x00000000000000000000000000010100)]

在这里，请注意 0x10100=00010000000100000000。0x10100=00010000000100000000。 然后，input = 00000000，这意味着父节点深度为 0。索引 256=100000000256=100000000 代表此左右事件：

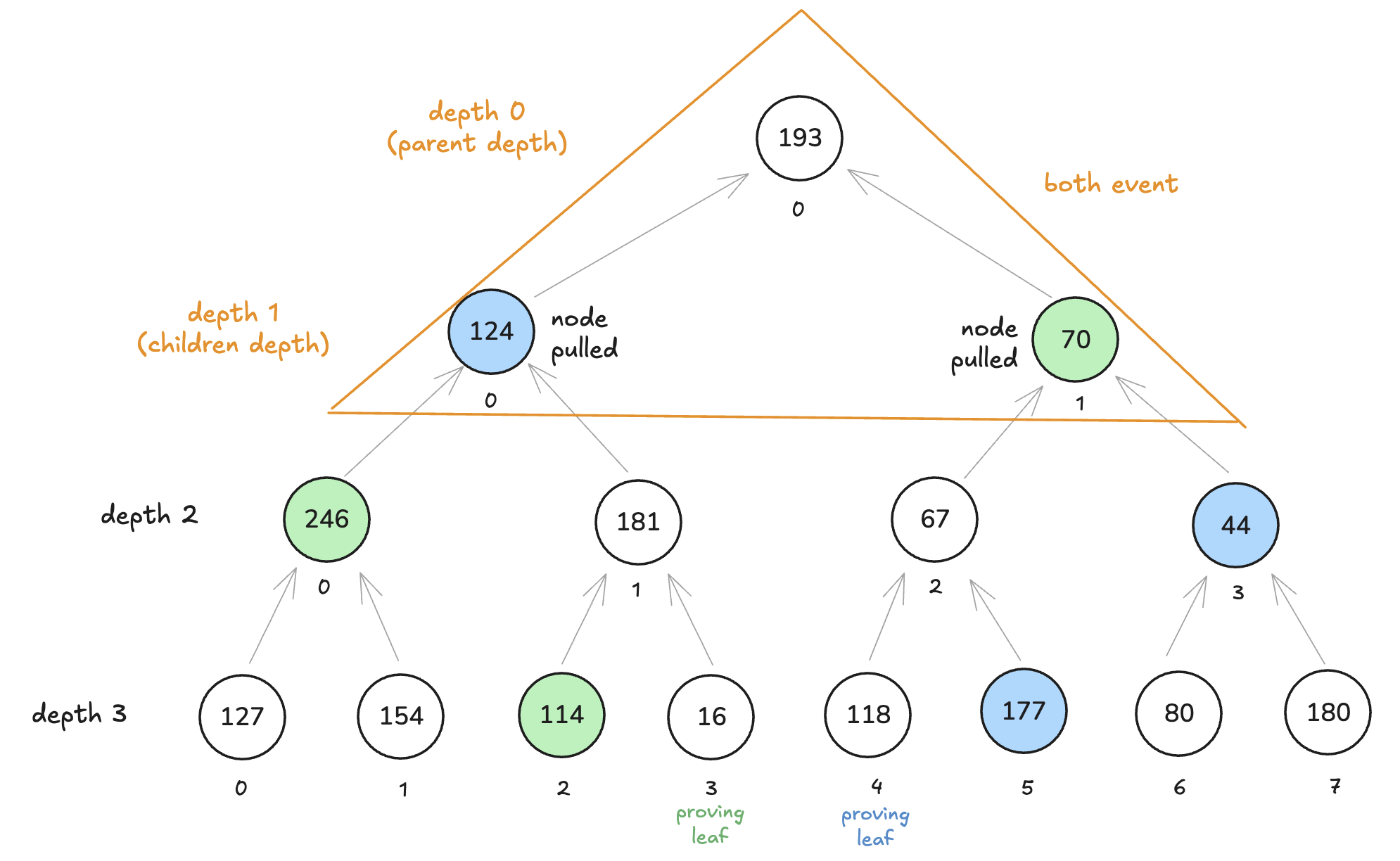
最后，你应该看到打印以下内容：

--- Processing table: merkle_tree_roots (ID: 3) ---

这意味着它处理了根表，但正如预期的那样，它没有找到来自查找通道的任何 pull out。

Sorted Counts

回想一下，我们试图了解 incr_table 是如何填充的。 在计算所有 lookup_counts 后，我们以特定的方式对其进行排序，将其存储在 sorted_counts 中，并使用它来填充表。

变量 sorted_counts 是一个包含 512 个元组的向量。 每个元组的第一个元素是一个索引，第二个元素是变量 lookup_counts 在该索引处的计数。 这些元组根据从最高到最低的计数进行排序。 让我们再次在函数 fill_tables() 中添加此打印，以便更好地理解它：

let lookup_counts = tally(cs, witness, &[], self.lookup_channel, &IncrIndexedLookup)?;

// 使用排序后的计数填充查找表
let sorted_counts = lookup_counts
    .into_iter()
    .enumerate()
    .sorted_by_key(|(_, count)| Reverse(*count))
    .collect::<Vec<_>>();

println!("------- Increment Table -------");
println!("Sorted counts: {sorted_counts:?}");

witness.fill_table_parallel(&self.incr_table, &sorted_counts)?;

这将打印：

------- Increment Table -------
Sorted counts: [\
    (257, 2), (258, 2), (256, 1), (0, 0), (1, 0), (2, 0), ..., (510, 0), (511, 0)\
]

IncrLookup 实例使用这些计数来填充其内部 entries_ordered 和 entries_sorted 列，并且其 LookupProducer 记录了 Merkle 树路径计算中发生的每个有效增量操作的确切多重性。

总结

这篇文章深入探讨了 Binius 的 M3 算术化框架，使用 Merkle 树包含证明作为一个具体的例子。 我们研究了表和通道如何作为 M3 中的基础抽象，用声明式的、数据驱动的模型取代了传统顺序执行的概念。 在这种范例中，计算被分解为模块化表，同时通过通道平衡来维持全局一致性。

该例子的核心是 MerkleTreeCS gadget，它协调五个专用表和多个通道来验证 Merkle 路径的正确性。 NodesTable 处理父节点-子节点关系的哈希处理，RootTable 将计算出的路径与预期的根值相关联，IncrLookup 表使用经过排列检查的查找结构来验证深度转换。 这些组件通过诸如 nodes_channel 和 lookup_channel 等通道进行通信，确保每个使用的值都得到正确生成和说明。

• 原文链接： blog.lambdaclass.com/div...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～