LazyTower: An O(1) Replacement for Incremental Merkle Trees

EthTaipei
发布于 2025-03-15 13:43
阅读 79

LazyTower是一种新的数据结构，旨在逐步添加项并适用于零知识证明的成员资格。其均摊成本为O(1)，电路复杂度为O(log N)。文章详细讨论了LazyTower的实现原理、成本分析及隐私保护机制，同时提供了相关的代码实现链接。

LazyTower 是一個資料結構. 它的用途和 Incremental Merkle Tree (IMT) 一樣: 讓使用者可以逐步地 append items, 並且適用於 zero-knowledge 的 proof of membership.

LazyTower append 一個 item 的 amortized cost 是 O(1).

Proof 的 circuit complexity 是 O(log N). Verification cost 是 O(1).

## 核心觀念

Items 會從最底下的 level 被 append. 如果一層滿了, 就把整層 digest() 起來並 append 到上層. 這樣下層就又有空間可以容納新的 items. 我們以 width = 4 的 tower 為例, 請看影片:

[LazyTower: The Core Idea](https://www.youtube.com/watch?v=3QeJgxB9ZiQ)

藉由儲存

```
digest([0, 1, 2, 3])
```

這個值, 我們可以在之後證明 item 0 1 2 3 曾經被 append 過.

藉由儲存

```
digest([digest([0, 1, 2, 3]),\
        digest([4, 5, 6, 7]),\
        digest([8, 9, 10, 11]),\
        digest([12, 13, 14, 15])])
```

這個值, 我們可以在之後證明 item 0 … 15 曾經被 append 過.

我們可以觀察到, tower 裡面儲存的每一格都是一個 Merkle root. 分別固定了 4⁰, 4¹, 4² … 個 item.

這一點可以從以下影片看的更清楚:

[LazyTower](https://www.youtube.com/watch?v=7MsGTO6CuqI)

## Cost

平均來說, 最下層在每 1 次 append item 會被修改到一次.

上一層在每 4 次 append item 會被修改到一次.

再上一層在每 16 次 append item 會被修改到一次.

由於每一層的寬度都相同, 操作也一樣, 所以如果最下層 append 的 cost (save 或 load+hash) 不會超過一個 constant C 的話, 每一個單層修改的 cost 也都不會超過同一個 C.

這樣平均來說, 一次 append 的 cost 不會超過

```
1 * C  +  1/4 * C  +  1/16 * C  + ...
= 1.333 C
```

## Privacy

當我們想證明某個 item 曾經被 append 過, 但是又不想直接揭露是哪個 item 時, 可以用 zero-knowledge proof 來證明其 membership.

我們可以用傳統的 Merkle proof 證明一個 item 屬於 tower 中的某個單一的 root. 比方說: “我的 item 隱藏在 level 10 的第二個 root 的 4¹⁰ 個 item 之中”.

如果我們只 load 一個 root 來證明 membership 的話, 雖然不會一下暴露是明確的哪一個 item, 但範圍就會從全部的可能幾千萬個縮小到這個 root 下的 4¹⁰ 個了. 當我們希望保留完整的 privacy 時, 則應該把 tower 中所有的 roots 都 load 起來, 再證明其 membership. 但這樣需要 O(log N) 的 cost, 並不理想.

我們能不能用一個單一的值來 “固定” 這些 roots, 使得證明 membership 時只要 load 一個值就好呢? 也就是說, 我只要 load 這個值, 則當別人舉出一個 root 時, 我就可以確認這個 root 是原本 tower 眾多 root 中的一個呢?

我們分成 “水平/垂直” 兩階段來改進.

## 改進一: 水平的 level digests

前面提到, 當一個 level 裝滿時, 我們會將其 digest 起來存到上層去, 比方說用 digest(\[0, 1, 2, 3\]) 這個值來 “固定” 0, 1, 2, 3. 如果我們選用的 digest function 可以 incremental 地計算, 則我們可以儲存最新的 digest 就好, 不用儲存 array of roots. 比方說, 我們可以採用 Merkle-Damgård construction, 搭配一個 ZK-friendly 的 hash function (如Poseidon hash):

```
digest([a]) = a
digest([a, b]) = H(a, b)
digest([a, b, c]) = H(H(a, b), c)
digest([a, b, c, d]) = H(H(H(a, b), c), d)
digest([a, b, c, d, e]) = H(H(H(H(a, b), c), d), e)
...
```

因為每一層都只會從最後面 append, 所以每次都是固定 load / hash / save / update length. 可以 incrementally 而不用從頭計算.

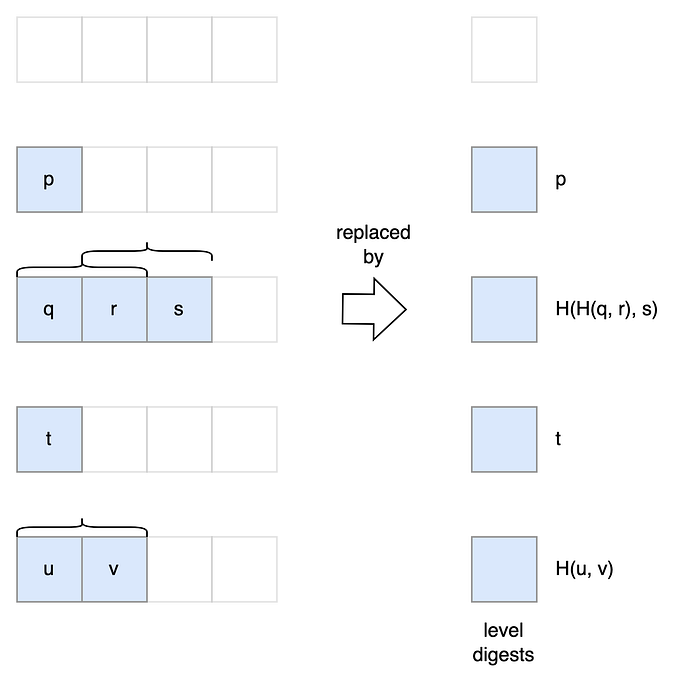
![](https://img.learnblockchain.cn/2025/04/09/1uEpQHzRDCLyWH09nk78ELg.png)

這樣在證明時, 每一層也只要 load 單一一個 level digest 就好.

但這樣我們仍然有 O(log N) 個值要 load 進 circuit 裡. 還有改進的空間嗎?

## 改進二: 垂直的 digest of digests

對於每個 level 的 digests, 我們可以垂直由上往下計算一個 digest of digests. 用這個值來固定所有 digests.

把頻繁更動的底層放在尾端, 這樣就可以藉由儲存 prefix 的結果來達成局部更新. 不用每次從頭計算.

也就是說, 我們會儲存這些值:

```
digest([d4]) = d4
digest([d4, d3]) = H(d4, d3)
digest([d4, d3, d2]) = H(H(d4, d3), d2)
digest([d4, d3, d2, d1]) = H(H(H(d4, d3), d2), d1)
digest([d4, d3, d2, d1, d0]) = H(H(H(H(d4, d3), d2), d1), d0)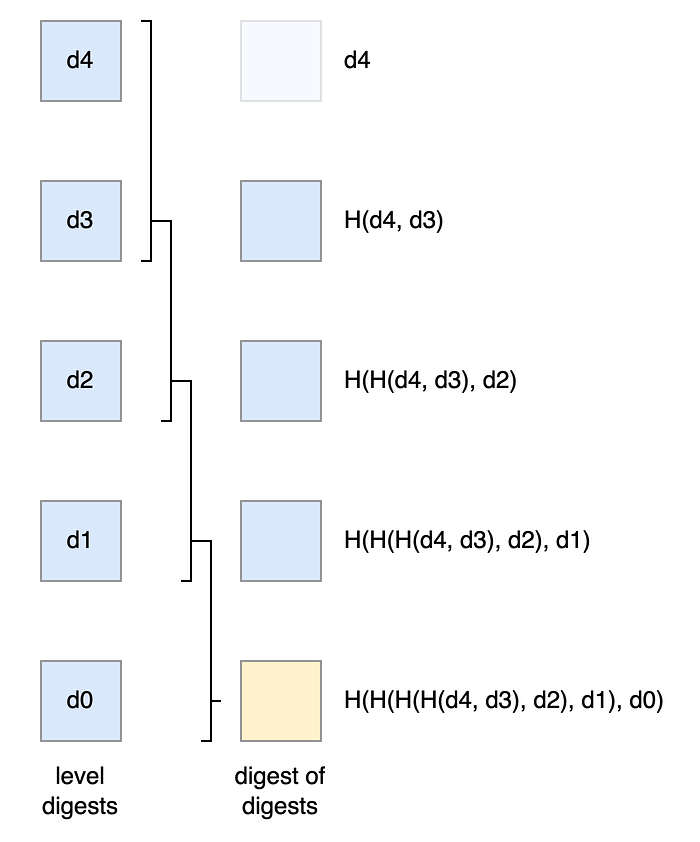
```

![](https://img.learnblockchain.cn/2025/04/09/1M1FcJxBXaBOUafgn5GusdQ.png)

當最下層的 d0 變了的時候, 我們可以不用整個重算 H(H(H(H(d4, d3), d2), d1), d0), 可以 load 先前儲存的 H(H(H(d4, d3), d2), d1), 再從後面局部更新 d0 進去.

當最下層的 d1 d0 變了的時候, 我們可以不用整個重算 H(H(H(H(d4, d3), d2), d1), d0), 可以 load H(H(d4, d3), d2), 再從後面局部更新 d1 d0 進去.

單一一層更新的 cost 也會是 constant. (load / hash / save)

## One to Rule Them All

於是我們得到了一個 digest of digests, 可以固定每個 level 的 digest. 每個 level digest 又固定了該 level 的 roots. 每個 root 又固定了那棵 tree 的 leaves, 也就是當初加進去的 items.

這樣在證明時, 我們只要 load O(1) 的資料就好了.

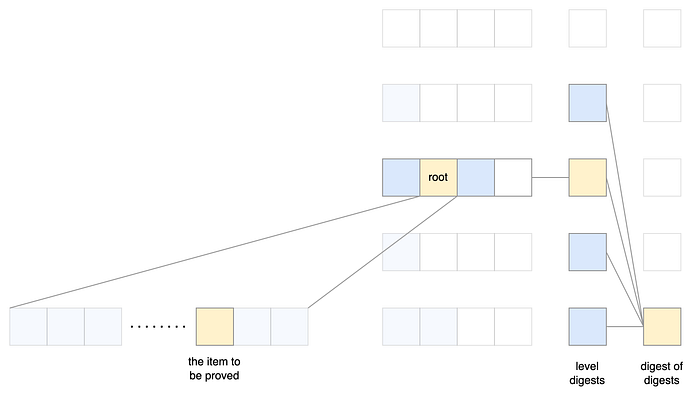
![](https://img.learnblockchain.cn/2025/04/09/1TQT6n8kY8WKB0Do3bBFynA.png)

1. 每層的 cost 仍然可以用一個共用的 constant bound 住
2. 越上層修改的頻率越低 (exponentially)

因此新增 item 的 amortized cost 仍然是 O(1).

## 實作

以下我們觀察實作的結果.

我們可以看到, 新增 item 的平均 gas 的確很快收斂到 constant. (21000 included)

而使用 width 較大的 tower, 平均的 gas 也較低, 但有其極限.

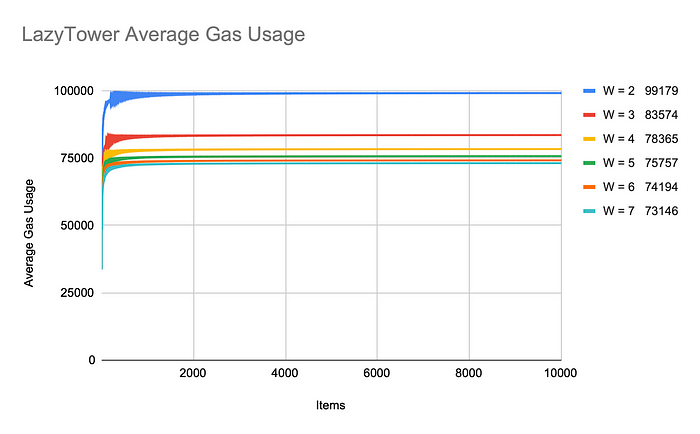
![](https://img.learnblockchain.cn/2025/04/09/1mLVknbjtU5UClfNsbHTeig.png)

和 Incremental Merkle Tree 相比, 即便要容納大量的 items, 使用者也不用擔心 gas 上升. 甚至也不用在一開始就決定容量上限.

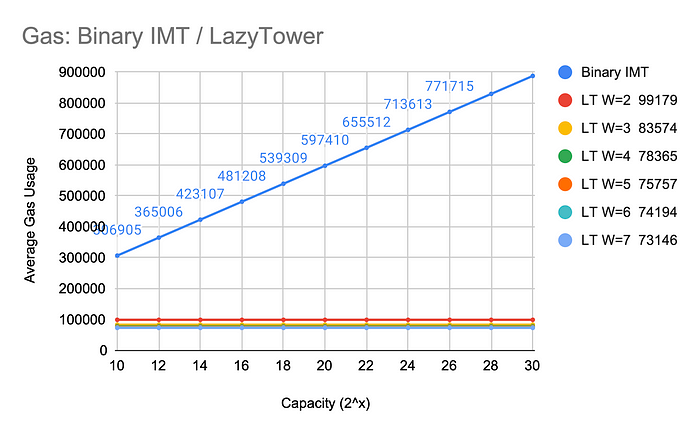
![](https://img.learnblockchain.cn/2025/04/09/1lU8ofH8lFZOz6eg2t8C70Q.png)

雖然提高 width 能稍微降低 gas, 但也會增加證明時的 circuit complexity.

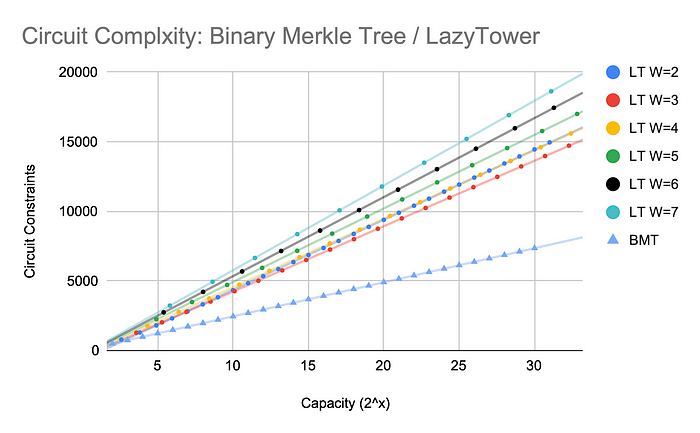
![](https://img.learnblockchain.cn/2025/04/09/1x6KnDMlkCHpyyzz7OmURTw.png)

Deploy 時通常會將 gas 和 circuit complexity 一起考慮. Width 取 4 到 7 是不錯的選擇.

## 結語

LazyTower 平均花費的 gas 是 O(1), Circuit complexity 為 O(log N), 且不用一開始就決定容量. 使用 Merkle Tree 的專案都可以考慮使用 LazyTower.

## Acknowledgement

我在 2023 年初有了初步的想法. 感謝 Ethereum Foundation 的 grant 讓我完成實作. 也感謝 reviewer 們的幫助!

實作目前由 PSE team 維護. 採 open source license 釋出.

- Javascript: [https://github.com/privacy-scaling-explorations/zk-kit](https://github.com/privacy-scaling-explorations/zk-kit)
- Solidity: [https://github.com/privacy-scaling-explorations/zk-kit.solidity](https://github.com/privacy-scaling-explorations/zk-kit.solidity)
- Circom: [https://github.com/privacy-scaling-explorations/zk-kit.circom](https://github.com/privacy-scaling-explorations/zk-kit.circom)

感謝 Taipei Ethereum Meetup 的 Martinet Lee 的審閱.

英文版: [https://ethresear.ch/t/lazytower-an-o-1-replacement-for-incremental-merkle-trees/21683](https://ethresear.ch/t/lazytower-an-o-1-replacement-for-incremental-merkle-trees/21683)

>- 本文转载自： [medium.com/taipei-ethere...](https://medium.com/taipei-ethereum-meetup/lazytower-an-o-1-replacement-for-incremental-merkle-trees-94d5a522dd89)

LazyTower 是一個資料結構. 它的用途和 Incremental Merkle Tree (IMT) 一樣: 讓使用者可以逐步地 append items, 並且適用於 zero-knowledge 的 proof of membership.

LazyTower append 一個 item 的 amortized cost 是 O(1).

Proof 的 circuit complexity 是 O(log N). Verification cost 是 O(1).

核心觀念

LazyTower: The Core Idea

藉由儲存

digest([0, 1, 2, 3])

這個值, 我們可以在之後證明 item 0 1 2 3 曾經被 append 過.

藉由儲存

digest([digest([0, 1, 2, 3]),\
        digest([4, 5, 6, 7]),\
        digest([8, 9, 10, 11]),\
        digest([12, 13, 14, 15])])

這個值, 我們可以在之後證明 item 0 … 15 曾經被 append 過.

我們可以觀察到, tower 裡面儲存的每一格都是一個 Merkle root. 分別固定了 4⁰, 4¹, 4² … 個 item.

這一點可以從以下影片看的更清楚:

LazyTower

Cost

平均來說, 最下層在每 1 次 append item 會被修改到一次.

上一層在每 4 次 append item 會被修改到一次.

再上一層在每 16 次 append item 會被修改到一次.

這樣平均來說, 一次 append 的 cost 不會超過

1 * C  +  1/4 * C  +  1/16 * C  + ...
= 1.333 C

Privacy

當我們想證明某個 item 曾經被 append 過, 但是又不想直接揭露是哪個 item 時, 可以用 zero-knowledge proof 來證明其 membership.

我們可以用傳統的 Merkle proof 證明一個 item 屬於 tower 中的某個單一的 root. 比方說: “我的 item 隱藏在 level 10 的第二個 root 的 4¹⁰ 個 item 之中”.

我們分成 “水平/垂直” 兩階段來改進.

改進一: 水平的 level digests

前面提到, 當一個 level 裝滿時, 我們會將其 digest 起來存到上層去, 比方說用 digest([0, 1, 2, 3]) 這個值來 “固定” 0, 1, 2, 3. 如果我們選用的 digest function 可以 incremental 地計算, 則我們可以儲存最新的 digest 就好, 不用儲存 array of roots. 比方說, 我們可以採用 Merkle-Damgård construction, 搭配一個 ZK-friendly 的 hash function (如Poseidon hash):

digest([a]) = a
digest([a, b]) = H(a, b)
digest([a, b, c]) = H(H(a, b), c)
digest([a, b, c, d]) = H(H(H(a, b), c), d)
digest([a, b, c, d, e]) = H(H(H(H(a, b), c), d), e)
...

因為每一層都只會從最後面 append, 所以每次都是固定 load / hash / save / update length. 可以 incrementally 而不用從頭計算.

這樣在證明時, 每一層也只要 load 單一一個 level digest 就好.

但這樣我們仍然有 O(log N) 個值要 load 進 circuit 裡. 還有改進的空間嗎?

改進二: 垂直的 digest of digests

對於每個 level 的 digests, 我們可以垂直由上往下計算一個 digest of digests. 用這個值來固定所有 digests.

把頻繁更動的底層放在尾端, 這樣就可以藉由儲存 prefix 的結果來達成局部更新. 不用每次從頭計算.

也就是說, 我們會儲存這些值:

digest([d4]) = d4
digest([d4, d3]) = H(d4, d3)
digest([d4, d3, d2]) = H(H(d4, d3), d2)
digest([d4, d3, d2, d1]) = H(H(H(d4, d3), d2), d1)
digest([d4, d3, d2, d1, d0]) = H(H(H(H(d4, d3), d2), d1), d0)