将PQC视为（主要）没有陷门的网络世界

将 PQC 视为一个（几乎）没有陷阱门的网络世界

我昨天参加了一个关于 PQC 的 NIST 研讨会，讨论的焦点是密码学灵活性。转向 PQC 基本上是我们从那些没有我们所需核心安全证明的方法迁移的自然组成部分。这些现有的方法现在看起来都有些过时，并且通常基于陷阱门方法。

陷阱门的问题在于，最终目标会发现陷阱在哪里，而不会掉入陷阱。对于许多现有的公钥方法，我们都使用了一个陷阱门——一种可以逆转运算的神奇方法。这种方法的强度就是陷阱门方法的强度。RSA 方法就是这种情况，它使用费马小定理来执行陷阱门。

许多新的后量子密码学方法避免了陷阱门技术，而专注于更困难的问题。对于最近定义的 NIST 数字签名标准，主要有两种方法：使用 Fiat-Shamir 方法进行非交互式处理的格方法（Dilithium — ML-DSA, FIPS 204），以及基于哈希的方法（SPHINCS+ — SLH-DSA, FIPS 205）：

我知道很难看清楚我的小涂鸦在表达什么，所以我将尝试用英语解释。

SPHINCS+ — 基于哈希的签名

在上面的图的右侧，我们看到了 Lamport 签名的方法，我们为 A 生成 256 个私钥，为 B 生成 256 个私钥。然后，公钥是所有这些密钥的哈希值（总共 512 个）。当我们签名时，我们获取消息的哈希值（得到 256 位的哈希值）。然后，我们遍历每一位，如果我们有一个 0，我们从 A 中选择关联的私钥。否则，我们从 B 中选择它。然后，我们遍历这些位，最终得到 256 个密钥，要么来自 A，要么来自 B。这给了我们一个 256x256 的签名大小（8kB）。验证时，我们检查每个哈希值是否包含在公钥中。当然，这是一个一次性签名，我们必须为下一个签名创建新密钥并重新发布我们的公钥。该方法在此处进行了说明 [ here]：

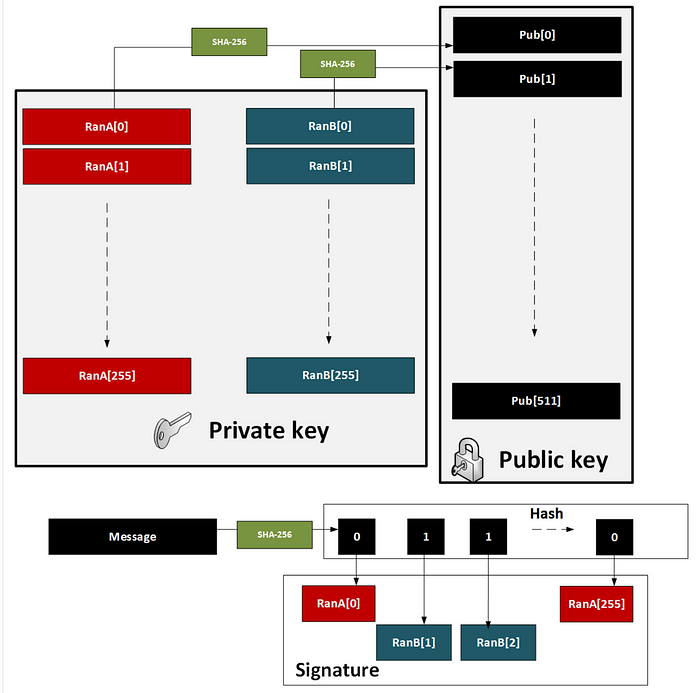
为了改进这一点，我们可以定义 WOTS+ 方法。该方法是：

• 最初，我们创建 32 个 256 位的随机数。这 32 个值将是我们的私钥。
• 然后，我们将每个值哈希 256 次。这 32 个值将是我们的公钥。
• 现在，我们获取消息并使用 SHA-256 对其进行哈希处理。这将产生 32 个 8 位的值（N1、N2 … N32）。
• 对于签名，我们获取消息哈希中的每个 8 位值，然后哈希 256-N 次（其中 N 是 8 位值的值）。
• 为了证明签名，我们使用 SHA-256 对消息进行哈希处理，然后获取每个 8 位值。然后，我们将 8 位签名值哈希消息哈希值定义的次数（N1、N2..）。每个运算的结果应等于公钥值。

这说明为 [ here]：

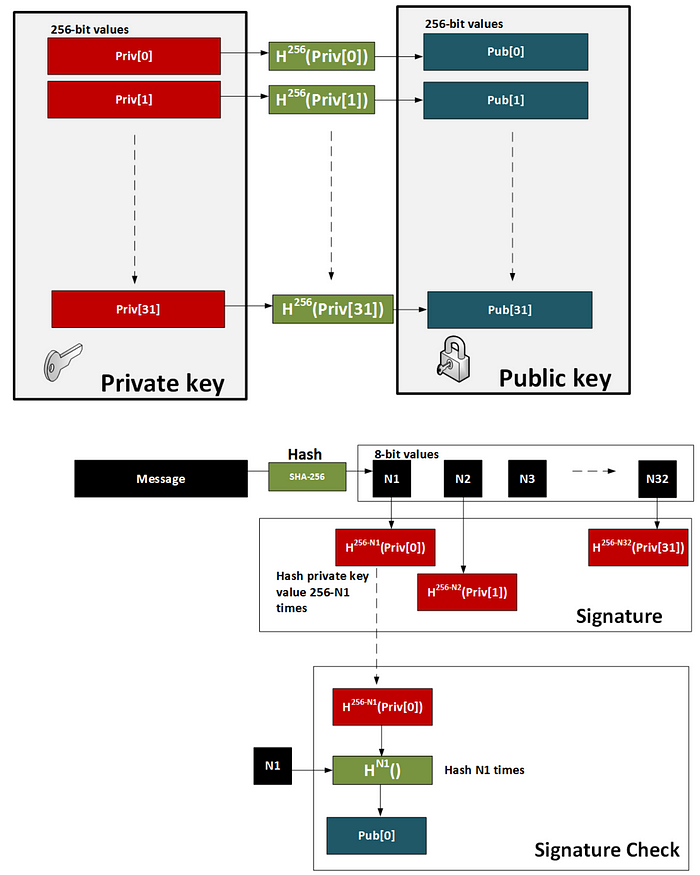
通过这种方式，我们减少了签名和公钥的大小。然后，我们可以生成公钥和私钥的 Merkle 根，并将它们缩小到单个 256 位的值。然后，我们可以创建这些密钥的树，以便我们可以多次签名并拥有不同的私钥，但仍然只有一个 256 位的私钥和一个 256 位的公钥。这就是 SPHINCS+ 使用的方法，它具有较小的公钥和私钥，但具有较大的签名（对于 128 位安全性，约为 17KB）：

Method                   Public key size    Private key size   Signature size  Security level
------------------------------------------------------------------------------------------------------
SPHINCS+ SHA-256 128-bit      32                 64             17,088         1 (128-bit)
SPHINCS+ SHA-256 192-bit      48                 96             35,664         3 (192-bit)
SPHINCS+ SHA-256 256-bit      64                128             49,856         5 (256-bit)

ML-DSA — 使用零知识证明的 Fiat Shamir 签名

现在，我们将看一下右侧，看看对于我们的基于格的签名生成方法，我们不再需要陷阱门：

创建基于格的签名的方法实际上基于 Schnorr 签名方法来证明身份（零知识证明），然后应用 Fiat-Shamir 方法使其成为非交互式的。基本上，它是秘密（一个人的私钥）的 NI-ZKP（非交互式零知识证明）。

如果 Bob 想要证明他知道一个秘密，他会创建一个短的随机秘密向量 (x)。然后，他创建一个随机矩阵数组 A 和一个包含小错误的错误矩阵 e1。他的公钥 (u) 是：

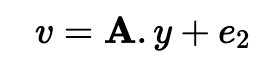
让我们忽略错误，因为它最终会在我们执行计算时被删除。所以让我们只使用：

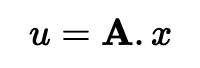
这个值将被发送给 Alice。然后，她可以向 Bob 发送一个挑战 (c)，这是一个随机整数值。然后，Bob 创建一个随机的短向量 y，并计算：

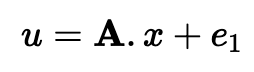
让我们再次忽略 e2，因为它最终会被删除。然后，Bob 使用 Schnorr 身份证明进行计算：

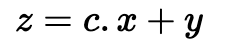
然后，Bob 将 x 和 v 发送给 Alice，她检查这些是否相等：

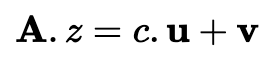
如果是，则 Bob 证明了他知道 x 的值（他的私钥）。这是因为：

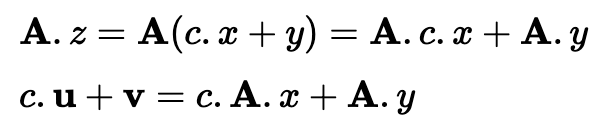
现在，我们可以通过使用 Fiat-Shamir 启发式方法将零知识证明转换为签名。有了这个，就不需要 Alice 发送挑战，因为 Bob 可以计算：

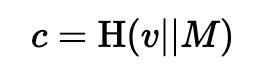
其中 M 是消息，“||” 是值的串联，H() 是哈希。然后，我们可以只执行相同的操作，Alice 将能够从消息和 v 的值中重新生成 c，并检查：

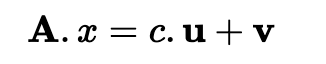
太棒了，并且没有陷阱门！[ here]

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～