椭圆曲线密码学中强大的基点（G）——什么是阶？

本文深入探讨了椭圆曲线密码学（ECC）中基点G的重要性，解释了其在密钥交换中的作用。通过具体示例展示了如何选择合适的基点以避免循环，并介绍了order的概念及其对安全性的影响。文章还给出了判断bad base point的例子，并介绍了secp256k1曲线的基点。

椭圆曲线密码学中强大的基点（G）——什么是阶？

你的在线安全高度依赖于曲线上一个简单的点——基点 G。每次你连接到网络时，你和服务器都在使用这个神奇的点来创建一个只有你和服务器知道的密钥。这是椭圆曲线 Diffie-Hellman 方法（ECDH）的基本机制，以及它对基点（G）的用法。

你可能认为 Diffie-Hellman 方法很酷，而 RSA 有一个巧妙的后门方法，但当你发现椭圆曲线密码学时，你才会真正看到密码学的美妙之处。我们最初的许多公钥和密钥交换方法都基于离散对数方法：

Y=g^x (mod p)

其中我们有一个基数 g 和一个素数 p。g 的值需要仔细选择，以便最大化 x 到 Y 的可能映射的数量，并且其中每一个都具有向后映射。如果你有兴趣，当我们选择正确的 g 和 p 值时，从 x 到 Y 的映射总数将是 p-1。这个值被称为映射的阶。因此：

Y = 7^x (mod 997)

将具有 996 的阶（因为 7 是 997 的安全生成器 [ 这里]）。但是椭圆曲线呢？嗯，它们在曲线上有一个基点 G，然后我们创建 2.G、3.G 等等。对于我们的私钥，我们可以有一个 priv 的标量，然后公钥将是 priv.G（这基本上是将 G 加 priv 次）。那么我们使用哪个基点重要吗？所以，就像在离散对数中一样，答案是肯定的！

在 ECC 中，我们有一个方程 y²=x³+ax+b (mod p)。这给出了我们在椭圆曲线上的点。对于 a=2，b=3 和 p=97，我们得到 [ 这里]：

(1,54) (1,43) (3,91) (3,6) (4,47) (4,50) (10,76) (10,21) (11,17) (11,80)
(12,94) (12,3) (17,87) (17,10) (20,34) (20,63) (21,73) (21,24) (22,92)
(22,5) (23,73) (23,24) (24,95) (24,2) (25,35) (25,62) (27,7) (27,90) (28,34)
(28,63) (29,54) (29,43) (32,7) (32,90) (37,22) (37,75) (38,7) (38,90) (39,91)
(39,6) (44,77) (44,20) (46,72) (46,25) (47,79) (47,18) (49,34) (49,63) (50,19) (50,78) (52,68) (52,29) (53,73) (53,24) (54,85) (54,12) (55,91) (55,6) (56,89) (56,8) (59,65) (59,32) (65,65) (65,32) (67,54) (67,43) (70,65) (70,32) (73,83) (73,14) (74,77) (74,20) (76,77) (76,20) (80,87) (80,10) (83,74) (83,23) (84,37) (84,60) (85,26) (85,71) (86,69) (86,28) (87,27) (87,70) (88,41) (88,56) (91,39) (91,58) (92,81) (92,16) (95,66) (95,31) (97,87) (97,10)

你可以用 (1,54) 检查，因为 54² (mod 97) 是 6，而 1³+2 x 1 + 3 (mod 97) 也是 6。对于 (3,91)，我们有 91² (mod 97)，它是 36，而 3³+ 2 x 3 + 3 (mod 97) 是 36。对于 x=2 和 x=5，没有解。

一个基本的图是 [ 这里]：

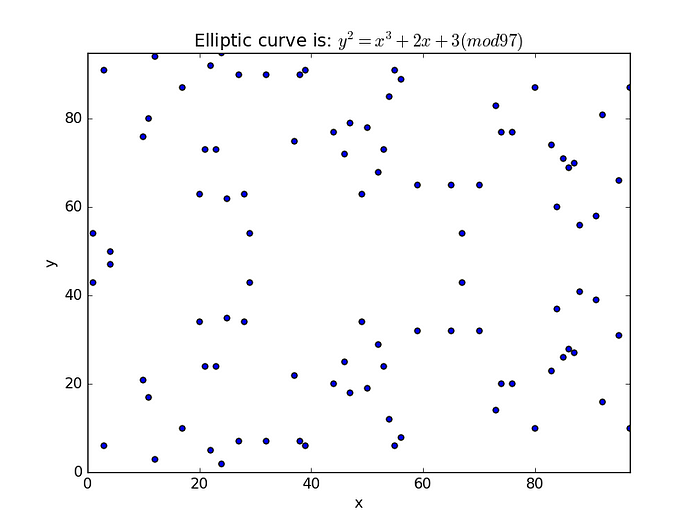
对于公钥加密，我们必须创建一个基点（G），然后将其添加 n 次（以获得 nG）。nG 的值将是我们的公钥，n 的值将是我们的私钥。但是我们如何选择一个基点呢？让我们尝试 (3,91) [ 这里]：

a= 2
b= 3
p= 97
n= 18
x-point= 3
P (3,91) Point is on curve
2P (80,87) Point is on curve
3P (80,10) Point is on curve
4P (3,6) Point is on curve
5P=0
6P (3,91) Point is on curve
7P (80,87) Point is on curve
8P (80,10) Point is on curve
9P (3,6) Point is on curve
10P=0
11P (3,91) Point is on curve
12P (80,87) Point is on curve
13P (80,10) Point is on curve
14P (3,6) Point is on curve
15P=0
16P (3,91) Point is on curve
17P (80,87) Point is on curve
18P (80,10) Point is on curve

我们可以看到这是一个坏的基点，因为它会循环。我们将这个点的阶 (N) 定义为 N=5。我们将其定义为由 P 生成的子群有 5 个点。我们可以用 Sage 检查这个：

a = 2
b = 3
p = 97

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

G = E(3,91)
print("Generator order q=", G.order())

这给出了：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
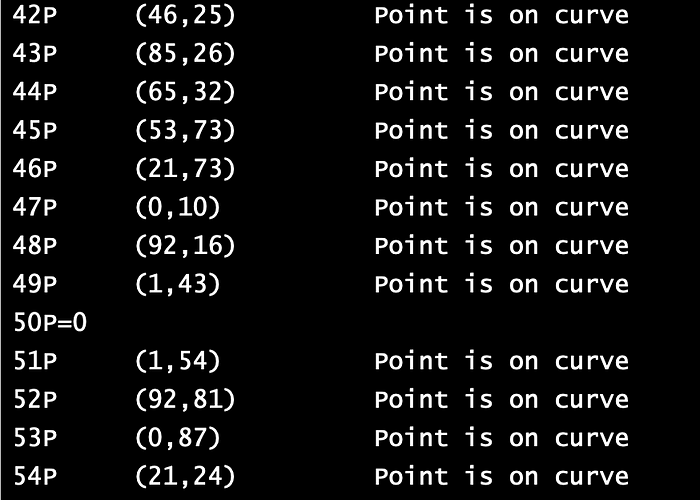
Generator order q= 5

现在让我们尝试 (1,54) 的基点 [ 这里]：

a= 2
b= 3
p= 97
n= 18
x-point= 1
P (1,54) Point is on curve
2P (92,81) Point is on curve
3P (0,87) Point is on curve
4P (21,24) Point is on curve
5P (53,24) Point is on curve
6P (65,65) Point is on curve
7P (85,71) Point is on curve
8P (46,72) Point is on curve
9P (23,73) Point is on curve
10P (3,6) Point is on curve
11P (87,70) Point is on curve
12P (52,29) Point is on curve
13P (47,18) Point is on curve
14P (74,20) Point is on curve
15P (88,41) Point is on curve
16P (32,90) Point is on curve
17P (17,87) Point is on curve
18P (95,31) Point is on curve

我们可以看到 (1,54) 构成了一个更好的基点，因为它在我们选择的 n 值的范围内没有循环。事实上，在这种情况下，由 P 生成的子群有 50 个点。

我们可以再次用 Sage 计算：

a = 2
b = 3
p = 97

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

G = E(1,54)
print("Generator order q=", G.order())

结果是：

Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
Additive abelian group isomorphic to Z/50 + Z/2 embedded in Abelian group of points on Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Finite Field of size 97
cardinality = 100
Generator order q= 50

应该注意到一件事，对于每个可达到的 x 坐标，我们有两个可能的 x 点。这意味着其中一个点是无用的，这将把可能的 256 位安全性降低到 128 位，因为我们将实际阶数减少了一半。

这是一些代码 [ 这里]：

## https://asecuritysite.com/encryption/ecc_points_mult
import sys
import libnum

a=0
b=7
p=37 # prime number
n=10 # number of points to show
x=3 # starting point

## y^2 = x^3 + ax + b (mod p)
print("a=",a)
print("b=",b)
print("p=",p)
print("n=",n)
print("x-point=",x)

if  (n>20): n=20

z=(x**3 + a*x +b) % p
if (libnum.has_sqrtmod(z,{p:1} )):
  y=next(libnum.sqrtmod(z,{p:1}))

print("P\t(%d,%d)" % (x,y), end=' ')

if ((y**2 % p) == ((x**3+a*x+b) %p)): print("  \tPoint is on curve")
else:
    print("  \tPoint is not on curve")
    sys.exit()

s=((3*x**2)+a) * libnum.invmod(2*y,p)

x1=(s**2-2*x) % p

y1=((s*(x-x1))-y) % p

x3=x1
y3=y1
x2=0
y2=0
counter=1

for i in range(2, n+1):
    counter=counter+1
    if (counter>n): sys.exit()

    print("%dP\t(%d,%d)" % (counter,x1,y1), end=' ')
    if ((y1**2 % p) == ((x1**3+a*x1+b) %p)): print("  \tPoint is on curve")

    rtn=libnum.invmod(x1-x,p)
    if (rtn==0):
        print("%dP=0" % (counter+1))
        counter=counter+2
        s=((3*x**2)+a) *  libnum.invmod(2*y,p)

        x1=(s**2-2*x) % p

        y1=((s*(x-x1))-y) % p
        print("%dP\t(%d,%d)" % (counter,x,y), end=' ')
        if ((y**2 % p) == ((x**3+a*x+b) %p)): print("  \tPoint is on curve")

    else:
        s=(y1-y)* rtn

        x2=(s**2-x1-x) % p

        y2=((s*(x1-x2)-y1)) % p

        x1=x2
        y1=y2

因此，在现实生活中，当我们选择一个基点时，我们会确保它具有较高的阶值，这样它就不会循环。对于 Sepc256k1（y²=x³+7 mod p），我们有一个基点和素数：

x = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
y = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

如果我们在 Sage 中尝试：

a = 0
b = 7
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

E = EllipticCurve(GF(p), [0,0,0,a,b])
print(E)
print(E.abelian_group())

card = E.cardinality()
print("cardinality =",card)
factor(card)

G = E(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8)
print("Generator order q=", G.order())

运行结果是：

Elliptic Curve defined by y² = x³ + 7 over Finite Field of size 115792089237316195423570985008687907853269984665640564039457584007908834671663
Additive abelian group isomorphic to Z/115792089237316195423570985008687907852837564279074904382605163141518161494337 embedded in Abelian group of points on Elliptic Curve defined by y² = x³ + 7 over Finite Field of size 115792089237316195423570985008687907853269984665640564039457584007908834671663
cardinality = 115792089237316195423570985008687907852837564279074904382605163141518161494337
Generator order q= 115792089237316195423570985008687907852837564279074904382605163141518161494337

我们可以用 Python 将其转换为十六进制：

hex(115792089237316195423570985008687907852837564279074904382605163141518161494337)

'0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141'

因此，N 的值将为我们提供核心安全级别，并将定义我们在循环之前可能的值的数量。

  • 原文链接： billatnapier.medium.com/...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
billatnapier
billatnapier
江湖只有他的大名，没有他的介绍。

billatnapier

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！