Dilithium(又名ML-DSA)与菲亚特-沙米尔方法的美妙世界
- billatnapier
- 发布于 2025-04-06 19:40
- 阅读 3769
本文介绍了Dilithium(又名ML-DSA)数字签名方案,它基于Fiat-Shamir方法和格密码学,是后量子密码学的重要组成部分。文章讨论了Dilithium的工作原理、密钥大小、性能以及两位关键贡献者Vadim Lyubashevsky和Chris Peikert,并提供了JavaScript实现示例。

Dilithium(又名 ML-DSA)的精彩世界和 Fiat Shamir 方法
当零知识证明方法变成数字签名
你知道零知识证明(ZKP)方法现在正被用于数字签名吗?我将在本文中解释,届时我们将遇到将 ZKP 方法扩展到具有量子鲁棒性的数字签名世界的两位核心构建者:Vadim Lyubashevsky 和 Chris Peikert。
介绍
过去一年里,我和构建了基于格密码学基础的人们进行了一些很棒的对话。其中包括 Vadim Lyubashevsky 和 Chris Peiker。他们两人实际上都不知道他们的工作会变得多么重要,但最终,通常是基于格的方法将被用于取代我们现有的 RSA 和 ECC(椭圆曲线密码学)方法。这包括 ML-KEM(又名 CRYSTALS Kyber — FIPS 203)、ML-DSA(又名 Dilithium — FIPS 204)和 FN-DSA(又名 FALCON — FIPS 206)。这些方法通常比其他 PQC 技术更快,并且通常具有可管理大小的密钥。
CRYSTALS Dilithium 使用基于格的 Fiat-Shamir 方案,并生成所有后量子方法中最小的签名之一,并且具有相对较小的公钥和私钥大小。使用的参数的三个主要实现是:Dilithium 2、Dilithium 3 和 Dilithium 5。总的来说,Dilithium 2 相当于 128 位签名,并且可能是实现的起点。CRYSTALS Dilithium 现在已被 NIST 标准化为 FIPS 204(ML-DSA),并定义为 ML-DSA-44(Dilithium 2)、ML-DSA-65(Dilithium 3)和 ML-DSA-87(Dilithium 5)。
Fiat Shamir 方法
总的来说,Fiat-Shamir 方法是一种零知识证明方法,它允许 Peggy 生成她自己的知识证明,而无需 Victor 向她发送挑战。在下面,Peggy 有一个秘密(x)并创建一个公共值(x.G),其中 G 是椭圆曲线上的一个基点。
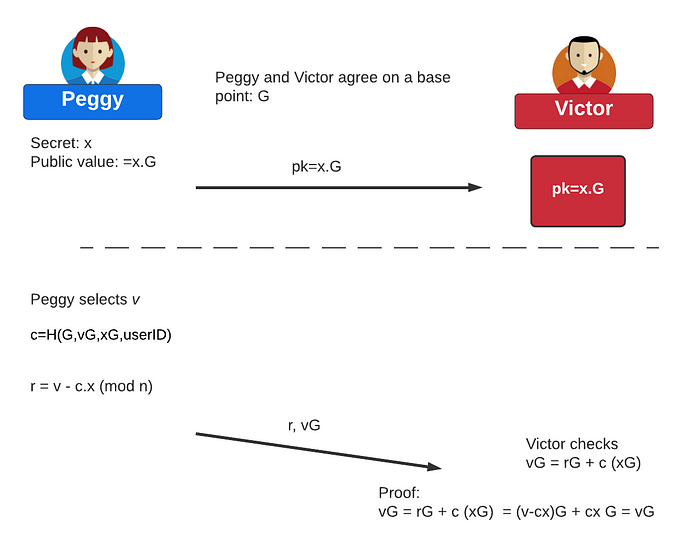
然后,Peggy 将生成一个随机标量值 v,并生成基点 G、v.G、x.G 和她的用户 ID(userID)的哈希值(c)。然后,她计算:
r= v -c.x (mod n)
其中 n 是曲线的阶数。她将此值发送给 Victor,后者检查:
v.G = r.G + c (x.G).
如果它们匹配,Peggy 已经证明她知道 x 的值。对于数字签名,秘密显然是 Peggy 的私钥,公共值是她的公钥。并且,她将签署一条消息(M),而不是她的 userID。
所以,现在让我们认识一下将此方法应用于格密码学世界的两个人:Vadim Lyubashevsky 和 Chris Peikert。
Vadim Lyubashevsky
Vadim Lyubashevsky 是 IBM Research Europe 在苏黎世的密码学家。他于 2008 年获得加州大学圣地亚哥分校的博士学位。他的核心研究重点是基于格的方法,尤其是在实用格加密、数字签名和隐私保护原语领域。他与 Chris Peiker 和 Oded Regev(LWE 的发明者)一起发表了一篇题为“论理想格和环上的带误差学习”的经典论文,该论文已被用作后量子密码学中格方法的基础。Vadim 曾在密码学的许多领域工作过,包括零知识证明、盲签名和多方计算。这是他:
Bill Buchanan OBE
•
他撰写的一篇经典文章概述了如何使用 Fiat-Shamir 方法来创建我们在 Dilithium 中看到的签名 [1]:

以及 [2]:

Chris Peikert
Chris 是密歇根大学计算机科学与工程系的教授。他于 2006 年在 Silvio Micali 的指导下在 MIT 计算机科学和人工智能实验室完成了博士学位。他因一篇题为“高效且可组合的 Oblivious Transfer 框架”的论文获得了 2008 年 Crypto 的 Test of Time 奖,并因其关于“从循环格的最坏情况假设中高效抗冲突哈希”的论文获得了 TCC Test of Time 奖,该论文于 2006 年发表。2024 年,Chris 当选为国际密码学研究协会的会士,并被视为基于格的方法的世界领导者之一。这是他:
Bill Buchanan OBE
•
Chris 与 Vadim 一起奠定了基于格密码学的许多核心原则,包括 [4]:

以及与强大的 Craig Gentry [5]:

Dilithium(又名 ML-DSA)
Dilithium 使用在格中查找短向量的难度,并使用 e “带有中止的 Fiat-Shamir”方法 [1, 2, 3]。对于密钥生成,我们从私钥 (sk) 和误差矩阵 (e) 中派生出公钥 (vk),以用于经典的 LWE(带误差学习)方法:
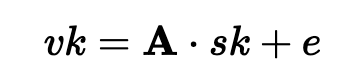
其中 A 是一个 k 乘 l 的矩阵,t 是一个 k 个元素的向量。这些都是取模 (q),其中 q 是一个素数。然后,验证密钥将是(A,vk),签名密钥将是 sk。要签名,我们创建一个短的临时秘密 (r) 和一条消息 (msg),并创建一个挑战承诺(其中 e′ 是 e 的一个样本):
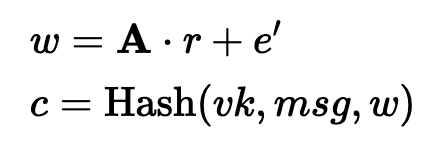
接下来,我们计算:
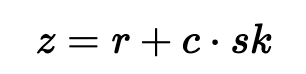
如果 z 太大,我们将重试。最后,我们将(w,z) 作为签名返回。这是一个经典的带有中止的 Fiat-Shamir sigma 方法。中止用于阻止签名密钥被泄露。要验证,我们首先检查 z 是否很小。接下来,我们计算:
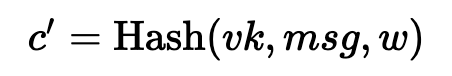
然后检查
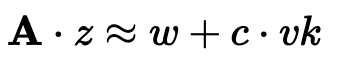
这是因为误差值将相对较小:
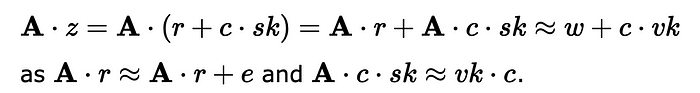
密钥大小
Dilithium 的密钥大小大于 RSA 和 ECC,但仍然可以管理,ML-DSA-44 的公钥为 1,312 字节,私钥为 2,528 字节,签名为 2,420 字节:
Method Public key size Private key size Signature size Security level
------------------------------------------------------------------------------------------------------
Crystals Dilithium 2 (Lattice) 1,312 2,528 2,420 1 (128-bit) Lattice
Crystals Dilithium 3 1,952 4,000 3,293 3 (192-bit) Lattice
Crystals Dilithium 5 2,592 4,864 4,595 5 (256-bit) Lattice
Falcon 512 (Lattice) 897 1,281 690 1 (128-bit) Lattice
Falcon 1024 1,793 2,305 1,330 5 (256-bit) Lattice
Sphincs SHA256-128f Simple 32 64 17,088 1 (128-bit) Hash-based
Sphincs SHA256-192f Simple 48 96 35,664 3 (192-bit) Hash-based
Sphincs SHA256-256f Simple 64 128 49,856 5 (256-bit) Hash-based
RSA-2048 256 256 256
ECC 256-bit 64 32 256对于 TLS 数据包,因此需要两个数据包才能发送 Dilithium 2 签名 - 这不应该有太大的开销。Dilithium 真正闪耀的是性能,它的密钥生成速度比大多数其他 PQC 方法快得多。以下是各种操作的每秒周期数的评估 [ 这里]:
Method Keygen Sign Verify
------------------------------------------------------------
Dilithium 2 300,751 1,081,174 327,362 (Unoptimized, Ref, Skylake)
Dilithium 3 544,232 1,713,783 522,267
Dilithium 5 819,475 2,383,399 871,609
Falcon-512 19,872,000 386,678 82,339 (Intel e5-8259U 2.3GHz)
Falcon-1024 63,135,000 961,208 205,128
SPHINCS+128f 9,649,130 239,793,806 12,909,924 * (3.1 GHz Intel Xeon E3-1220 CPU (Haswell)
SPHINCS+192f 14,215,518 386,861,992 19,876,926
SPHINCS+256f 36,950,136 763,942,250 19,886,032因此,Dilithium 是一种不错的全能型方法,这也是它被 NIST 选为 FIPS 204 标准的原因之一。
编码
为了演示该方法,我在此处创建了一个 JavaScript 程序:
此代码位于 [ 这里]:
<script type="application/javascript" src="/dilithium.js"></script>
<style>
.dropdown {
font-size: 16px;
border: 2px solid grey;
width: 100%;
border-left: 12px solid green;
border-radius: 5px;
padding: 14px;
}
pre {
font-size: 16px;
border: 2px solid grey;
width: 100%;
border-left: 12px solid green;
border-radius: 5px;
padding: 14px;
}
textarea {
font-size: 20px;
border: 2px solid grey;
width: 100%;
border-radius: 5px;
padding: 14px;
}
</style>
<div class="indented">
<h2>ML-DSA</h2>
<table width="100%">
<tr>
<th width="15%" valign="top">Key size</th>
<td style="text-align:left">
<p>
<input id="genkey" class="btn btn-large btn-primary" type="button" value="Re-generate Keys" />
</p>
</td>
</tr>
<tr>
<th width="15%" valign="top">Message</th>
<td>
<textarea cols="20" id="message" name="message" rows="2" style="width:100%"></textarea>
</td>
</tr>
<tr>
<th width="15%">Method</th>
<td>
<div class="dropdown">
<select name="method" id="method">
<option value="2">ML-DSA-44</option>
<option value="3">ML-DSA-65</option>
<option value="5">ML-DSA-87</option>
</select>
</div>
</td>
</tr>
<tr>
<th width="15%" valign="top">Signature</th>
<td>
<pre id="sign" valign="top"></pre>
</td>
</tr>
<tr>
<th width="15%" valign="top">Verify</th>
<td>
<pre id="verify"></pre>
</td>
</tr>
</table>
<h2>Generated keys</h2>
<table width="100%">
<tr>
<th width="15%" valign="top">Public Key</th>
<td>
<pre id="publicKey"></pre>
</td>
</tr>
<tr>
<th width="15%" valign="top">Private Key</th>
<td>
<pre id="privateKey"></pre>
</td>
</tr>
</table>
</div>
<script type="application/javascript">
(async function () {
var privateKey, publicKey;
for (let key of Object.keys(DilithiumAlgorithm)) {
window[key] = DilithiumAlgorithm[key];
}
function genKey() {
const level = DilithiumLevel.get(Number(document.getElementById('method').value));
const keyPair = DilithiumKeyPair.generate(level);
privateKey = keyPair.getPrivateKey();
document.getElementById('privateKey').innerText = "Length: "+privateKey.getBytes().length+'\n';
document.getElementById('privateKey').innerText += privateKey.toHex();
publicKey = keyPair.getPublicKey();
document.getElementById('publicKey').innerText = "Length: "+publicKey.getBytes().length+'\n';
document.getElementById('publicKey').innerText+= publicKey.toHex();
}
function sign() {
const level = DilithiumLevel.get(Number(document.getElementById('method').value));
const message = document.getElementById("message").value;
signature = privateKey.sign(message);
document.getElementById('sign').innerText= "Length: "+signature.getBytes().length+'\n';
document.getElementById('sign').innerText += signature.toHex();
valid = publicKey.verifySignature(message, signature);
if (valid) {
document.getElementById('verify').innerText = "Valid Signature";
} else {
document.getElementById('verify').innerText = "Invalid Signature";
}
}
document.getElementById("message").value = "Hello 1234";
genKey();
sign();
document.getElementById("genkey").addEventListener("click", genKey);
document.getElementById("genkey").addEventListener("click", sign);
document.getElementById("message").addEventListener("input", sign);
})();
</script>OpenSSL
我们在线安全的大部分基础通常建立在 OpenSSL 之上,本周将发布一个新版本 - 3.15.0 - 它集成了 ML-DSA:
没有借口:OpenSSL 进入量子时代 \ \ 认识 ML-KEM (FIPS 203)、ML-DSA (FIPS 204) 和 SLH-DSA (FIPS 205)\ \ medium.com
结论
没有任何借口了。后量子密码学(PQC)的方法现在已经确定,我们现在必须考虑迁移我们现有的密钥交换和数字签名方法。
参考文献
[1] Lyubashevsky, V. (2009, December). Fiat-Shamir with aborts: Applications to lattice and factoring-based signatures. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 598–616). Berlin, Heidelberg: Springer Berlin Heidelberg.
[2] Lyubashevsky, V. (2012, April). Lattice signatures without trapdoors. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 738–755). Berlin, Heidelberg: Springer Berlin Heidelberg.
[3] Güneysu, T., Lyubashevsky, V., & Pöppelmann, T. (2012). Practical lattice-based cryptography: A signature scheme for embedded systems. In Cryptographic Hardware and Embedded Systems–CHES 2012: 14th International Workshop, Leuven, Belgium, September 9–12, 2012. Proceedings 14 (pp. 530–547). Springer Berlin Heidelberg.
[4] Lyubashevsky, V., Peikert, C., & Regev, O. (2010). On ideal lattices and learning with errors over rings. In 加粗Advances in Cryptology–EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, May 30–June 3, 2010. Proceedings 29** (pp. 1–23). Springer Berlin Heidelberg.
[5] Gentry, C., Peikert, C., & Vaikuntanathan, V. (2008, May). Trapdoors for hard lattices and new cryptographic constructions. In 加粗Proceedings of the fortieth annual ACM symposium on Theory of computing** (pp. 197–206).
- 原文链接: billatnapier.medium.com/...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 构建一个极简的后量子以太坊客户端:ethlambda 的架构 128 浏览
- 以太坊签名方案解析:ECDSA、BLS、XMSS 以及带 Rust 代码示例的后量子 leanSig 262 浏览
- 配对密码学之美:聚合签名和阈值签名 250 浏览
- 配对密码之美:聚合签名和阈值签名 368 浏览
- Shamir份额的魔力:BLS门限签名 361 浏览
- 英国银行与后量子密码 192 浏览
- Solana安全检查清单:Anchor和原生程序的45个关键检查项 395 浏览
- 量子计算与区块链:匹配紧迫性与实际威胁 914 浏览
- 基于哈希函数的签名(四):XMSS 和 SPHINCS 507 浏览
- 基于哈希函数的签名(二):少量次数签名 821 浏览
- Zig 签名(Ed25519 和 ECDSA) 1162 浏览
- 基于哈希函数的签名(一):一次性签名 783 浏览

