破解近乎单向函数

密码学

破解近乎单向函数

对于我们的标准数学，我们有一个函数 f(x)，然后能够反转它以找到 f^{-1}(x)。这可以是：

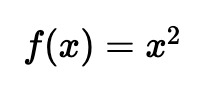
其中反转是结果的平方：

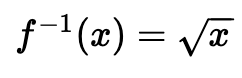
但是，是否可能有一个单向函数，而我们无法反转它？嗯，人们认为可能存在不可逆的单向函数，但尚未找到。然而，现在有一些候选的单向函数，它们易于计算，但极难反转。这些可以定义为单向置换，它们是：

• 模 p 指数运算。 这是指我们有 f(x)=g^x (mod p)，其中 p 是一个素数，即使我们知道 f(x)、g 和 p，也很难确定 x。
• RSA 函数。 这是指我们无法确定 f(x)=x^e (mod n) 的 x。在这个公式中，n=pq，其中 p 和 q 是大素数，并且选择 e 以不与 (p-1)(q-1) 共享因子。
• Rabin 函数。 在这种情况下，我们有 n=pq，其中 p 和 q 是等于 3 (mod 4) 的素数。然后我们有 f(x)=x² (mod n)，这会产生一个伪随机序列，其中无法知道 x。

但是，让我们用后门函数破解 Rabin 函数：

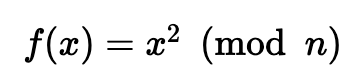
通过这个，我们可以创建一个伪随机序列。例如，我们可以有 p=23 和 q=7，它们都等于 3 (mod 4)。然后我们得到 n=161 的 Blum 整数。如果我们使用种子值 x=59，我们得到以下序列：

P=23
Q=7
N=161, phi=132
Seed=59
1 Current=100  \\ 59^2 mod (161)
2 Current=18   \\ 100^2 mod (161)
3 Current=2    \\ 18^2 mod (161)
4 Current=4
5 Current=16
6 Current=95
7 Current=9

因此，随机序列将是 100、18、2、4，依此类推。应该不可能确定 x 的先前值，因为它是一个单向置换（显然，我们使用小的素数，否则是有可能实现的），并且我们只能向前而不能向后。但是，通过一些魔法——了解原始素数——我们可以使用以下函数进行反转：

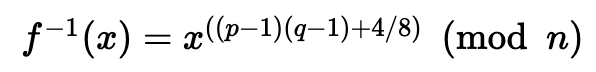
这是尝试此操作的 Python 代码 [ here]:

import random
import sympy
import sys

def next_usable_prime(x):
 p = sympy.nextprime(x)
 while (p % 4 != 3):
  p = sympy.nextprime(p)
 return p

bits=8

if (len(sys.argv)>1):
    bits=int(sys.argv[1])

p = next_usable_prime(random.randint(1,2**bits))
q = next_usable_prime(random.randint(1,2**bits))

N=p*q

print(f"P={p}")
print(f"Q={q}")
phi=(p-1)*(q-1)

print(f"N={N}, phi={phi}")

x=random.randint(1,N)
print(f"Seed={x}")

for i in range(1,21):
 x=pow(x,2,N)
 x_inv=pow(x,((p-1)*(q-1)+4)//8,N)
 print(f"{i} Current={x} Previous={x_inv}")

8 位素数的示例运行给出 [ ]:

P=239
Q=103
N=24617, phi=24276
Seed=10648
1 Current=18619 Previous=12321
2 Current=10567 Previous=18619
3 Current=23394 Previous=10567
4 Current=18709 Previous=23394
5 Current=22175 Previous=18709
6 Current=6050 Previous=22175
7 Current=21638 Previous=6050
8 Current=12321 Previous=21638
9 Current=18619 Previous=12321
10 Current=10567 Previous=18619
11 Current=23394 Previous=10567
12 Current=18709 Previous=23394
13 Current=22175 Previous=18709
14 Current=6050 Previous=22175
15 Current=21638 Previous=6050
16 Current=12321 Previous=21638
17 Current=18619 Previous=12321
18 Current=10567 Previous=18619
19 Current=23394 Previous=10567
20 Current=18709 Previous=23394

在这种情况下，p 是 239，q 是 103，n=24517。

我们可以看到，除了第一个值之外，该公式能够获取当前值，然后计算出 x 的先前值。这是一个后门函数，如果不花费合理的时间知道 p 和 q，应该不可能执行反转。你可以在此处尝试代码：

破解伪随机序列 \ \ Blum Blum Shub (BBS) 用作伪随机数生成器（它是伪的，因为它不是真正的随机数，而且…\ \ asecuritysite.com

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～