密码学 101：从何开始

我首先要说明，我绝对不是数学家，也不是加密学专家——我只是一个努力自学这门技艺的普通人。

正是因为如此，我尝试将我所碰到的复杂概念提炼成易于理解的部分。所以这就是我尝试呈现这些概念的结果。我一直相信，理解事物的运作方式是一种深刻的充实，尽管我们可能并不需要实现或真正使用我们学到的所有想法。希望你在这个过程中玩得愉快！

在这篇文章中，我们将探讨一些加密技术背后的基本概念，并在之后的时间构建这些概念。奠定这些基础在理解如 加密、秘密共享 等过程时将显得非常重要。

开始

在我的例子中，我在一家使用 区块链 技术的公司工作。这需要对 数字签名 有基本的理解——你知道，一些用户有一个 私钥，使用这个私钥来 签名一条消息，而签名的真实性可以通过 公钥 检查。这是相当常见的术语，很多库都可以执行我刚才描述的动作。

但从我的角度看，这感觉毫无不同于魔法。这到底是如何工作的？什么机制允许这种特定的过程？这种好奇心最终驱动了这篇文章的撰写。

然而，这样的冒险不能通过解释数字签名机制如何工作开始。我们必须首先奠定一些数学基础，以理解加密协议和技术是如何运作的。所以这将是我们的起点。

群

有很多基于 数学群 的加密技术。实质上，群 只是一个 元素集 和一个 二元运算（我们暂时用“+”表示）的组合，这个运算接受集合中的两个元素，并输出该集合中的另一个元素。这非常抽象——而实际上，没有任何东西阻止我们使用像这样的集合：

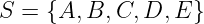
但随后我们必须定义组合 每对元素 时所产生的结果（即 A + B 的结果是什么？B + A 的结果相同吗？）。

幸运的是，有一些 更简单定义 的群。其中一个群基于整数——如果我们将整数限制在某个阈值 q 以下，我们会得到如下形式的集合：

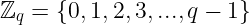
在不深入数学严谨性的情况下，我们把这个集合称为 模 q 的整数。而将 标准加法 作为群运算是很自然的：1 + 2 产生 3，这是该集合的一个元素，2 + 2 产生 4，等等。对于很多整数，这都是正确的，前提是 q 足够大！但有一个问题出现了：如果我们“越界”会发生什么？例如，如果我们尝试加：

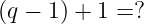
会发生什么？黑洞？栈溢出？

啊啊啊啊啊！

好吧……其实是的！我们只是 返回 到我们集合的 开头，得到 0。这发生是因为我有点撒谎：群运算不仅仅是标准加法，它是 模加法。所以我们必须定义这是什么以继续。

模运算

实际上，当我们说 模加法 时，我们指的是 模 运算。而这个运算就是把一个数字 a 除以某个模数 q 的余数。一般来说，以下关系成立：

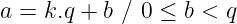
因此，当除 a / q 时，我们将得到一些整数 k 和一些余数 b。模运算的结果就是余数，我们写作：

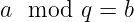
酷！有了这个，我们可以完成之前提到的群运算的定义：它是标准加法，加上模 q 运算的应用。我们刚刚定义的是被称为 模 q 的整数的加法群。这个简单的构造将在我们后续的分析中隐含或显式地存在，所以记住这一点是好的！

群生成元和子群

现在让我们重新关注如何理解群。特别是，让我们检查 q = 5 的例子。现在选择集合中的一个元素，例如 g = 2。如果我们不断地将群运算应用于 g 与 它自己，会发生什么？

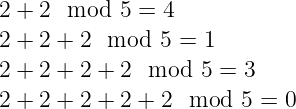
注意到发生了一些有趣的事情：我们通过 g 的重复加法产生了 群中的每个元素。这使得 g = 2 在某种程度上“特殊”——我们说它是该群的 生成元，因为我们在这个过程有效地“生成”了所有相关的集合。我们通常用 ⟨ g⟩ 表示由元素 g 生成的群。

我们还可以观察到，在前面的例子中，群中的每个元素 竟然都是生成元——你可以自己尝试一下。这并不是巧合：这和群中元素的个数（称为 群的阶，用 # 表示）实际上是个 素数 的事实有关。我们只是指出这一点，但目前不必太在意。

然而，如果我们选择不同的 q，那么并不是每个元素都必须是生成元。例如，如果 q = 6，则元素 2 就 不是 生成元：我们只会生成集合 { 0, 2, 4 } ——我们遇到了由 g=2 生成的 循环子群。

关于子群有一个有趣的属性，表述在 拉格朗日定理 中，其中指出：

每个有限阶群 G 的子群 S 的阶是 G 阶的一个因子；即，#S 整除 #G。

子群及其性质在群密码学中起着重要作用，因此我们稍后将再次回到这些事实。

总结

在这次简要的介绍中，我们介绍了一些基本数学概念。这些将作为今后文章的基础。

仅仅理解模运算及其 性质 就足以描述一些加密技术（如 RSA 加密）——但还有其他有趣的群我们尚未定义。在 下一篇文章 中，我们将深入探索 椭圆曲线 的世界，之后我们将利用它们设计一些 加密协议。

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～