可证明的水印提取

zkDL++ 是一个为可证明 AI 设计的新型框架。利用 zkDL++，我们解决了生成式 AI 水印的一个关键挑战：在确保可证明性的同时保持隐私。通过增强 Meta 开发的水印系统，zkDL++ 解决了需要保持水印提取器私有以避免攻击的问题，从而提供更安全的解决方案。除了水印，zkDL++ 还能高效地证明任何深度神经网络 (DNN) 的完整性。在这篇文章中，我们概述了我们的方法，评估了其性能，并提出了进一步优化的途径。

引言

Stable Signature 是 Meta AI 推出的一种水印 (WM) 方案，用于识别由其潜在扩散模型 (LDM) 生成的图像。它使用Rollup神经网络 (CNN) 来提取 WM，并且具有很强的图像篡改鲁棒性，即使图像经过过滤、裁剪、压缩等处理，也可以进行检测。然而，Stable Signature 存在必须保持提取器模型私有的缺点，因为暴露它会使 WM 容易受到攻击。如果在某个时候出现关于特定图像所有权的争议，这个缺点可能会很严重。虽然 Meta 或任何其他使用此类 WM 方法的公司都可以运行提取器并看到某个图像是由他们的模型生成的，但他们无法向社交媒体用户等第三方证明这一点，除非他们暴露提取器模型的权重。这种暴露可能导致 WM 系统的过时。

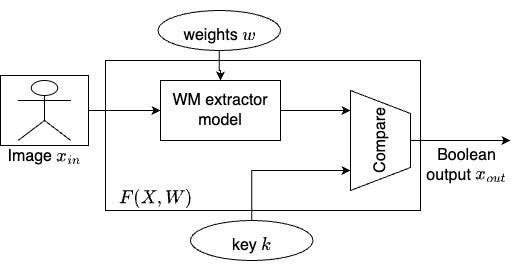
我们建议使用新兴的零知识证明 (ZKP) 技术来解决这个问题。在 ZKP 方案中，证明者希望说服验证者他们知道一个证人 𝑊，该证人服从某个函数关系 𝐹(𝑋,𝑊) = 0，而不泄露 𝑊。关系 𝐹 通常由算术电路表示，并且是公开的。变量 𝑋 包含电路的公共输入和输出。在 Stable Signature 的情况下，关系 𝐹 是 WM 提取器的架构，其输出与密钥进行比较，并且当且仅当从输入图像提取的 WM 与密钥匹配时才成立。公共变量

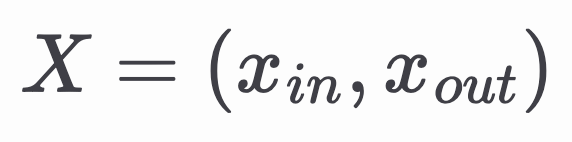
包括图像和布尔输出，私有证人

𝑊 = (𝑤,𝑘) 包括提取器的权重和密钥，如上图所示。然后，验证者可以运行验证算法，测试证明，如果关系确实成立，则返回 True，否则返回 False。

另一个挑战是确保权重不是故意选择的，以便为给定的图像产生特定的结果。幸运的是，这个问题可以通过以下方式轻松解决：

可证明水印提取的实际应用

根据 Meta 的说法，最终目标是在社交平台上标记 AI 生成的内容。像 Stable Signature 这样的技术可以通过将强大的水印嵌入到 AI 生成的媒体中来显着提高检测精度。Meta 可以将这些水印添加到其模型生成的内容中，但用户无法独立验证它们，因为提取器模型的权重必须保持私有。此外，每个公司（如 Google）都有自己的专有水印系统，与其他公司不兼容，这使得这一挑战更加复杂。

ZKP 完美地弥补了这种系统的缺点。对于 AI 生成的图像（同样的方法也适用于音频），Meta 可以附加水印提取的证明，类似于数字签名，而无需泄露敏感的模型细节。然后，客户端可以为其 feed 中的每个图像运行 ZK 验证，从而实现 AI 生成内容的自动标记。此外，像 Google 这样的其他公司可以集成他们自己的水印提取证明，从而使系统能够区分不同的 AI 模型。

Meta 将处理运行证明者的资源密集型任务，而客户端（例如移动设备）可以处理轻量级验证。由于水印对转换（如裁剪或压缩）具有鲁棒性，Meta 可以重新运行证明者以考虑任何转换并生成新的证明，如 VIMz 等方法所演示的那样。

DNN 的完整性证明

在Meta 的 Stable Signature中，水印提取器是专门设计用于分析加水印图像的 CNN。让我们关注尺寸为 128 × 128 像素的图像。下图显示了 Meta 提取器 DNN 的架构，它由 9 个Rollup层、一个平均池化层和一个全连接层组成。该模型包含大约 3800 万个参数。

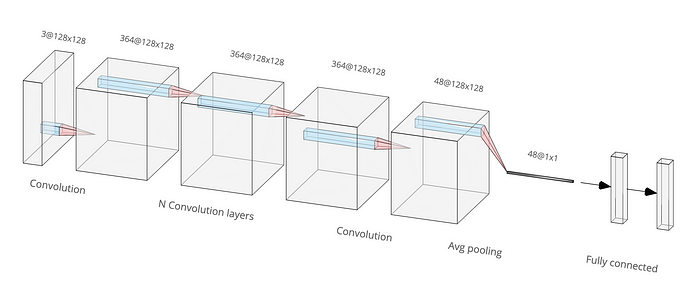
当前用于证明 DNN 推理的行业解决方案通常依赖于 zkVMs。然而，zkVM 不是特定于应用程序的，并且引入了不必要的复杂性，使其不太适合此任务。相比之下，最近的两篇学术论文，zkCNN 和 zkDL，提出了为证明 DNN 推理量身定制的 SNARK 框架，两者都基于 Sumcheck 协议。

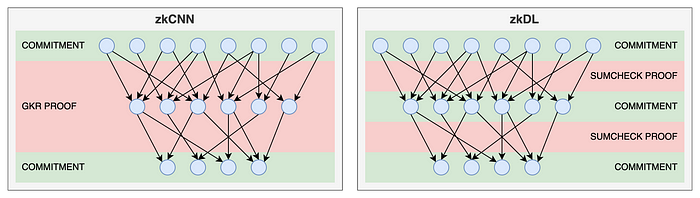
如下图所示，zkCNN 利用 GKR 协议，而 zkDL 独立地证明 DNN 的每一层。两者之间的权衡很明显：

• zkCNN 仅提交网络的输入和输出，而 zkDL 需要提交所有中间层间值。
• 然而，zkDL 允许并发处理层证明，而 zkCNN 必须按顺序处理它们。
• zkDL 的另一个优势是其灵活性——每个层证明都可以使用不同的证明系统，只要保持共享承诺即可。

在下一节中，我们将概述我们如何整合 zkDL 和 zkCNN 的概念来开发 DNN-SNARK 框架的概念验证，我们称之为 zkDL++。

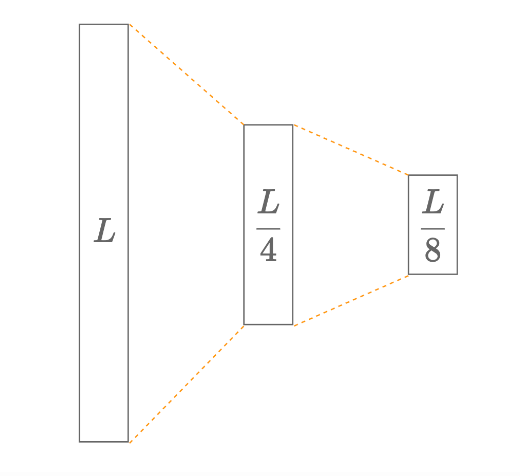
在我们深入研究我们的实现之前，让我们首先比较由两个全连接层组成的网络的证明构造运行时间。此分析评估 zkDL/zkDL++、Jolt zkVM 和 SP1 zkVM。如下图所示，大小为 𝐿 的网络输入在第一个全连接层中减少到大小 𝐿/4，然后通过第二个全连接层，产生大小为 𝐿/8 的输出。输入和网络参数都是均匀随机化的。

我们首先在所有三个框架中实现该模型。我们将输入向量采样为随机字节向量，并在三个框架中对全连接层的计算（即矩阵向量积）进行算术化。然后是证明生成和基准测试。我们的评估代码可在 [zkDL++] (https://github.com/ingonyama-zk/zkdl-plus/tree/sb/bench-op)（即将推出）、[Jolt](https://github.com/suyash67/jolt/tree/sb/compare) 和 SP1 中找到。

比较表明，zkDL/zkDL++ 在证明者运行时间性能方面优于 Jolt 和 SP1，尤其是在输入大小增加时。虽然 Jolt 和 SP1 在输入较大时性能会显着下降，但 zkDL/zkDL++ 保持相对较低的运行时间，使其成为需要高性能和可扩展性的系统的理想选择。例如，当输入大小为 2¹⁰ 时，zkDL 生成证明的速度比 SP1 快约 200 倍，如下图中的证明者运行时间图所示。

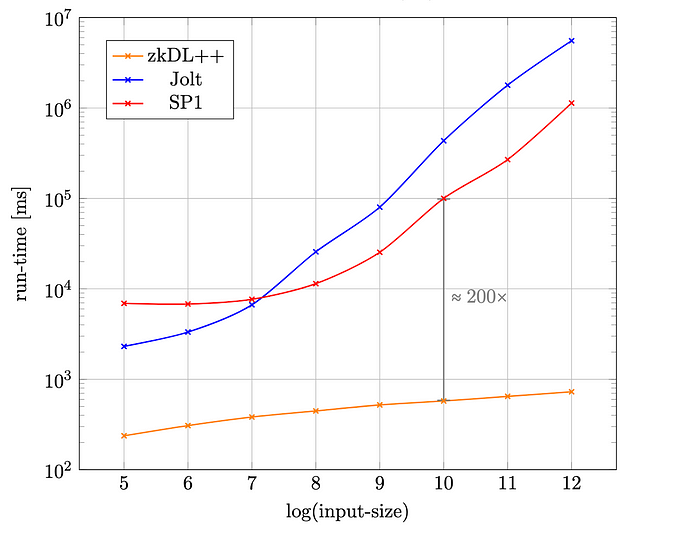
在这种情况下，模型参数的数量为 0.3 百万——仍然远低于典型的 DNN 模型。在这种情况下，zkDL++ 可能是唯一能够实际生成完整性证明的框架。

值得注意的是，所有实验都是在相同的硬件配置上进行的，该配置包括强大的 CPU（第 13 代 Intel Core i9–13900K）和高端 GPU（NVIDIA GeForce RTX 4080）。虽然该机器配备了强大的 GPU，但实验并未经过专门优化以充分利用 GPU 的潜力。GPU 优化可能会产生更快的结果，但这并不是我们实验的重点。

zkDL++

zkDL++ 可以看作是 zkDL 和 zkCNN 的混合体，旨在优化这两种方法。虽然 zkDL 和 zkCNN 代表两个极端——独立证明每一层与将整个网络作为一个整体进行证明——但 zkDL++ 在它们之间取得了平衡。这种灵活性允许高度的计算并行性，同时保持可管理的承诺成本。

我们的概念验证建立在 zkDL 的一个分支之上。最初，zkDL 仅支持全连接层和 ReLU 层的基元。通过添加对Rollup层和平均池化层的支持，我们能够为水印提取器 DNN 构建 SNARK。在以下部分中，我们将介绍概念验证的运行时结果，深入研究证明原语的数学基础，并总结讨论局限性和未来方向。

结果与方法

我们运行端到端 SNARK 证明器来证明提取器 DNN 推理的正确性。计算分为以下步骤。

1. 预处理：我们提交 DNN 的参数，即经过训练的 DNN 模型的权重和偏差。一旦模型经过训练，这就是一次性计算。
2. 推理：我们使用提取器 DNN 在随机输入（大小为 3 × 128 × 128）上运行推理。在 SNARK 的上下文中，此步骤称为证人生成。
3. 证人承诺：我们通过首先承诺证人来开始生成证明。具体来说，我们单独承诺每一层的输入和输出。
4. Sumcheck 证明：然后，我们计算每一层的 sumcheck 证明，以证明每一层单独的正确性。接下来计算每一层中证人多项式的开放证明。

我们在与上一节中描述的相同的硬件上对 zkDL++ 框架进行基准测试。下表显示了每个步骤的运行时间。

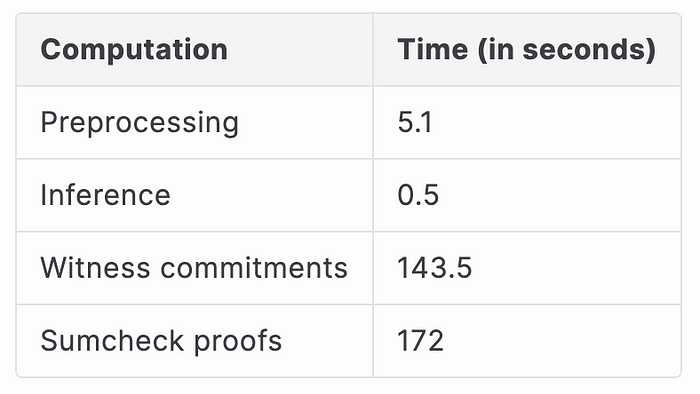
生成证明的总时间约为 5.4 分钟。接下来，我们讨论我们的技术概述。目标是将 DNN 中使用的基元进行算术化。

Rollup

为了简洁起见，我们将重点关注一维Rollup的算术化。设 𝑢 和 𝑣 分别是长度为 𝑛 的向量，表示Rollup的输入和输出，并设 𝑓 是长度为 2𝑡+1 的滤波器。

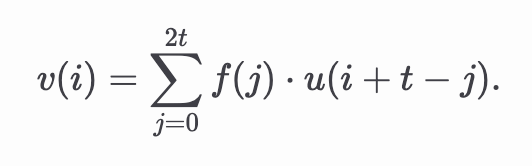
我们的目标是将输入 𝑢 和滤波器 𝑓 之间的Rollup表示为多项式方程。设 𝑝ᵤ(𝑥) 和 𝑝𝒻(𝑥) 分别是对应于 𝑢 和 𝑓 系数的多项式，如下所示

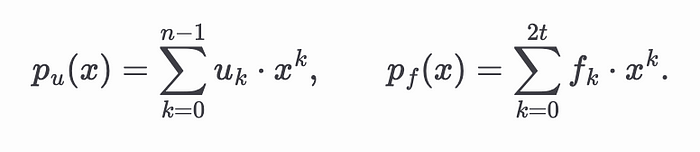
将 𝑝ᵤ(𝑥) 和 𝑝𝒻(𝑥) 相乘会产生 𝑢 和 𝑓 的Rollup。为了可视化这一点，请考虑以下来自 Wikipedia 的示例。

当将两个多项式 𝑃 和 𝑄 相乘时，将相同颜色的项相加会得到Rollup。但是请注意，尾部项作为乘法的残余出现，它们不是Rollup的一部分。使用这种方法，我们得到

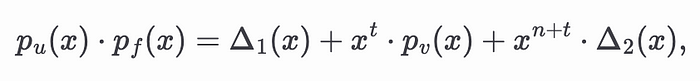
平均池化

正如 Justin Thaler 在 此处 演示的那样，可以使用 sumcheck 有效地证明矩阵乘法。因此，可以使用 sumcheck 验证平均池化操作的正确性。但是，当验证者需要在挑战上评估与上述方程中的常数矩阵相对应的双变量多项式时，会出现一个小挑战

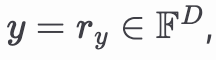
这意味着验证者的线性工作。为了避免这种情况并确保有效的验证，我们可以利用矩阵的结构，如下所示

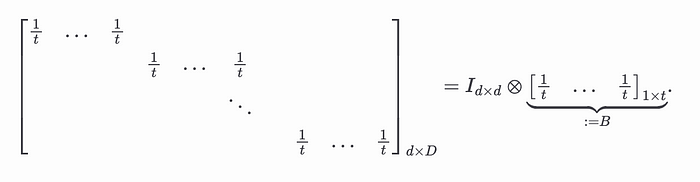
证明者可以利用这种张量积结构来构建更有效的 sumcheck，因为它本质上是不同变量中两个多线性多项式的乘法。

全连接

全连接层将权重矩阵应用于输入向量以生成输出向量。设 𝑢 为输入向量，𝑣 为输出向量，如下图所示。

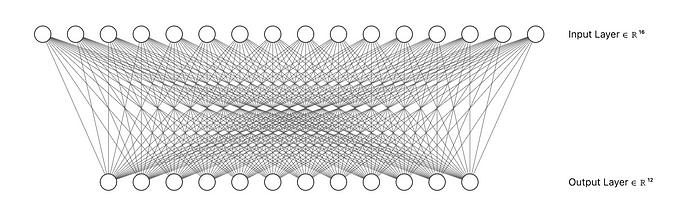
此操作表示为矩阵向量积

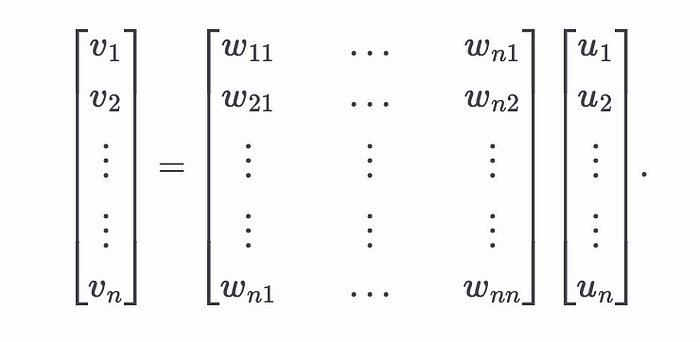
如平均池化示例中所述，我们可以使用矩阵乘法的 sumcheck 技术来证明全连接层的正确性。请注意，权重矩阵作为预处理的一部分被提交。

ReLU

zkDL 论文给出了一种将 ReLU 函数作为 sumcheck 实例进行算术化的技术。由于 ReLU 是一种非线性运算，因此我们需要一种略有不同的方法来进行算术化。为了便于说明，我们将演示单个 ReLU 函数的算术化。设 𝑢 为 ReLU 函数的输入，𝑣 为其输出。ReLU 函数应用于输入的缩放版本，如下所示

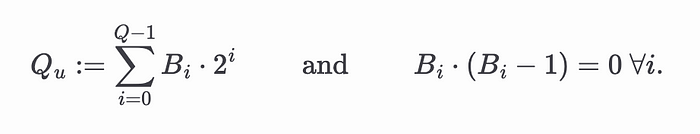
局限性和未来工作

目前的证明生成过程大约需要 5.4 分钟，当扩展到内容制作时，这可能显得资源密集。此时间的大部分花费在两个关键任务上：计算证人承诺和生成 sumcheck 证明。目前，这些操作是按顺序执行的，这会带来低效率，可以加以解决。

1. 顺序证人承诺：证明生成涉及计算 13 个证人向量的承诺，对应于 9 个Rollup层、1 个平均池化层、1 个全连接层以及输入和输出。目前，这些承诺是以线性方式逐层计算的，从输入开始并进行到输出。这种顺序过程会产生瓶颈，尤其是在处理大型模型时。并行化这些证人承诺的计算是一个直接且有希望的改进领域。
2. 批量 Sumcheck 证明：每一层还需要生成 sumcheck 证明，这些证明独立验证该层的不同属性。目前，sumcheck 证明是按顺序计算的，这进一步延长了证明生成时间。可以跨层并行化 sumcheck 证明，因为它们是独立的。此外，在每一层中，需要多个 sumcheck 证明来证明各种语句。批量处理这些 sumcheck 计算——在单个层内和跨不同层——可以帮助减少冗余并提高整体性能。
3. 承诺方案的选择：当前的实现使用 Hyrax 多线性承诺方案进行证人承诺和 sumcheck 开放证明。虽然 Hyrax 有效，但探索替代方案（例如 Zeromorph）可能是有益的，特别是对于需要零知识评估证明的应用程序。Zeromorph 在零知识设置中提供了潜在的性能和安全性优势。
4. 字段的选择：当前设置使用 BLS12–381 椭圆曲线及其对应的标量字段进行计算。虽然此曲线已被广泛用于加密目的，但探索替代字段（例如梅森素数或 Baby Bear（及其扩展））可能会加快证明生成过程。

有几个有希望的途径可以提高证明生成的效率。并行化证人承诺和 sumcheck 证明、探索替代承诺方案以及试验更小的字段代表了未来优化的重要机会。

接下来是什么？

在这项工作中，我们使用涉及 CNN 的真实示例演示了 zkDL++。但是，zkDL++ 框架非常灵活，可以扩展以支持其他层，使其适用于任何深度神经网络 (DNN)。在我们的私有水印提取概念验证中，我们为标准 CNN 实现了分钟级的证明者运行时。通过进一步的优化，我们相信这可以减少到几秒钟，满足 Meta 等公司的大规模部署的性能要求。

我们的代码已准备好投入生产并可供测试。我们鼓励合作者、研究人员和开发人员与我们一起探索 zkDL++，并帮助推进这个强大的框架。

鸣谢

我们要感谢 zkDL 和 Stable Signature 论文的作者。特别感谢 Pierre Fernandez 和 Haochen Sun。

关注 Ingonyama

Twitter: https://twitter.com/Ingo_zk

YouTube: https://www.youtube.com/@ingo_zk

GitHub: https://github.com/ingonyama-zk

LinkedIn: https://www.linkedin.com/company/ingonyama

加入我们: https://www.ingonyama.com/career

• 原文链接： medium.com/@ingonyama/pr...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～