有限域F p上的MiMC-Feistel(双分支Feistel网络)
- billatnapier
- 发布于 2025-08-13 08:25
- 阅读 1837
本文介绍了MiMC-Feistel密码,它是一种对称密钥加密方法,基于Feistel网络,并在有限域上进行操作。MiMC-Feistel在多方计算、全同态加密和零知识证明等领域具有应用前景,并且相比AES,其复杂度更低。
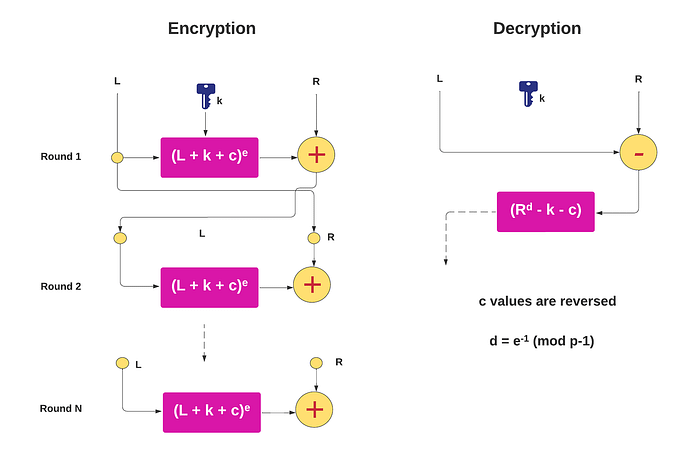
F_p 上的 MiMC-Feistel(双分支 Feistel 网络)
AES 很棒,但还有另一种执行对称密钥加密的方法:使用 Feistel 网络。 这样,我们就减少了大量的复杂性,并在由素数定义的有限域上执行操作。 这一特性使我们能够为诸如零知识证明之类的东西创建更简单的电路。 因此,让我们看看 MiMC-Feistel 的实现 [1]。
Feistel 网络
有些人可能认为网络安全的根源可以追溯到 20 世纪 80 年代第一个计算机蠕虫的发现,或者是 20 世纪 70 年代末公钥加密和 Diffie-Hellman 方法的发现。 但是,我们可以将其追溯到 20 世纪 70 年代初,以及 Horst Feistel 的工作。 他在 IBM 的工作可以追溯到 Feistel 密码的创建,该密码实现了一种对称密钥方法。
在 20 世纪 60 年代,大多数密码学研究都是由政府进行的,但 IBM 发现了一个商业机会,并在其位于纽约州约克敦高地的实验室成立了一个密码学研究小组(并以 IBM 创始人 - Thomas J. Watson Sr. 的名字命名)。 该实验室继续取得了惊人的进步,例如 DRAM、关系数据库和 FORTRAN 编程语言:

Thomas J Watson 研究中心 — 约克敦高地
他们最好的招聘人员之一是 Horst Feistel,一位物理学家出身的密码学家,他在 20 世纪 70 年代加入了他们。 他的工作促成了 Lucifer 和 DES(数据加密标准)密码的创建:

在 20 世纪 70 年代初,IBM 为 Lucifer 密码申请了专利,然后 Lloyds Bank 在第一批 ATM 自动取款机中使用了该密码。 在 NSA 的评估之后,Lucifer 的密钥大小从 112 位减少到 56 位,之后于 1975 年作为 DES 标准发布。 然后,DES 在美国政府电子资金转账中的使用成为强制性的,并最终成为事实上的国际标准。
Feistel 密码本质上使用相同的加密和解密过程,并且密钥应用只是颠倒了。 基本结构如下,我们将输入数据分成块。 然后将每个块分成两部分(左和右)。 那么每一轮都是:
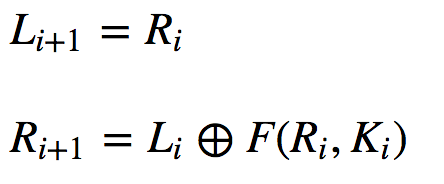
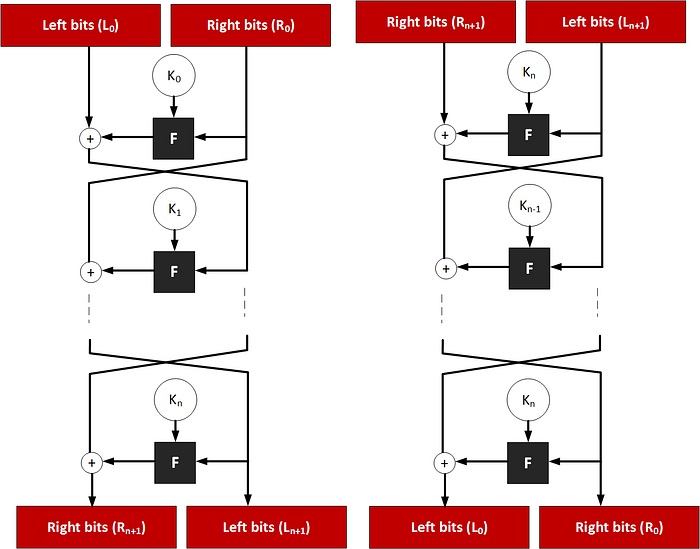
应用的函数 (F) 不必是可逆的,这与 AES 的情况不同。 对于 AES,我们有 S 盒,用于使用字节值之间的已定义映射来扰乱轮次。 此外,在 AES 中,我们在加密和解密过程之间有一个反函数,而 Feistel 只是以相反的顺序应用密钥。
MiMC-Feistel
MiMC(最小乘法复杂度)哈希 [1] 具有低乘法复杂度的重要特征,该特征用于多方计算 (MPC)、全同态加密 (FHE) 和 ZKP 领域。 Dan Bohen 等人 [2] 还提出了将其用于 VDF(可验证延迟函数),因为 MiMC 的复杂度仅为 AES 的 1.6%。
在原始论文中,有一个映射:
F( x)= x ³
在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的故事
免费加入 Medium,以获取来自这位作者的更新。
总的来说,我们有一个包含 q 个元素的有限域 ( Fq),并使用 r 次的 round 函数进行迭代 - 其中 q 是一个素数。 在每一轮中,我们添加一个密钥 (k) 值和一个轮常量 (ci) - 除了第一轮 - 以及 F( x)= x 3 的非线性函数:

如果 e =3 不起作用,那么我们可以使用 x ⁷:
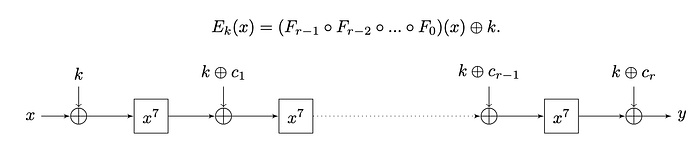
对于 F_p 上的 MiMC-p/p 密钥置换密码,我们执行:
x ←( x + k + ci) e(mod p)
对于 i =0… T −1
其中 k 是密钥,c 是每一轮的常量值,x 是置换后的密码。 对于解密过程,我们使用:
d = e^{ −1} (mod p −1)
来反转操作。 总的来说,我们需要选择一个 e 值与素数 (p) 互质,其中 gcd( e, p)==1。 此处的实现是:
现在,让我们将此密码转换为 Feistel 网络。 为此,我们有许多轮加密和解密,以及一个密钥 (k) 和一个常量值数组 (c[i])。 我们现在可以将输入分成两部分:左 (L) 和右 (R),然后应用 Fiestel 网络:
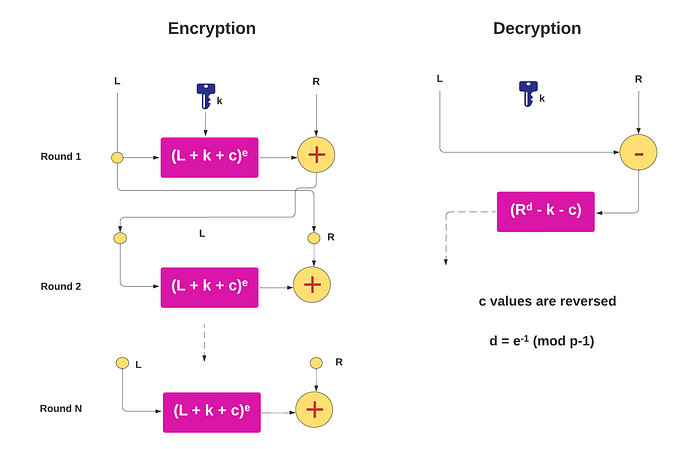
解密部分基本上执行相同的过程,但顺序相反。 轮常量定义为:
c_i = H(seed || i) mod p
其中 seed 值是一个常量字符串。 它的实现是 [ 这里]:
import hashlib
import math
import sys
from typing import List, Tuple
def _hash_to_int(data: bytes) -> int:
return int.from_bytes(hashlib.sha256(data).digest(), "big")
def derive_round_constants(n_rounds: int, p: int, seed: str) -> List[int]:
""" 使用 SHA-256 从种子中获取轮常量 (c_i),并在 F_p 中
c_i = H(seed || i) mod p.
"""
constants=[]
seed_b = seed.encode()
for i in range(n_rounds):
h = _hash_to_int(seed_b + i.to_bytes(4, "big")) % p
constants.append(h)
return constants
class MiMCFeistel:
"""在 F_p 上实现一个双分支 MiMC-Feistel。
对于加密,我们有:
t = (L + k + c_i)^e mod p
L, R = R, (R + t) mod p
对于解密,我们反转
"""
p: int
e: int=3
rounds: int = 91
seed: str = "Test"
constants = []
def encrypt(self, L: int, R: int, k: int) -> Tuple[int, int]:
L %= p
R %= p
k %= p
for c in self.constants:
t = pow((L + k + c) % p, e, p)
L, R = R, (R + t) % p
return L, R
def decrypt(self, L: int, R: int, k: int) -> Tuple[int, int]:
L %= p
R %= p
k %= p
for c in reversed(self.constants):
# 反转一个 Feistel 轮
t = (R - L) % p
inv_e = pow(e ,-1, p - 1)
L_prev = (pow(t, inv_e, p) - k - c) % p
R_prev = L
L, R = L_prev, R_prev
return L, R
Lin=20403023
Rin=1043391
key=123212312
p = 21888242871839275222246405745257275088548364400416034343698204186575808495617
e = 3
## 确保 gcd(e,p-1)==1
while (math.gcd(e,p-1)!=1):
e=e+2
rounds = 91
seed = "Test"
cipher = MiMCFeistel()
cipher.p=p
cipher.e=3
cipher.rounds=rounds
cipher.seed=seed
cipher.constants=derive_round_constants(rounds, p, seed)
if (len(sys.argv)>1):
Lin=int(sys.argv[1])
if (len(sys.argv)>2):
Rin=int(sys.argv[2])
if (len(sys.argv)>3):
key=int(sys.argv[3])
if (len(sys.argv)>4):
p=int(sys.argv[4])
L = int(Lin)
R = int(Rin)
k = int(key)
print(f"Key:\t{k}")
print(f"Prime:\t{p}")
print(f"Rounds:\t{rounds}\n")
print(f"Input left:\t{L}")
print(f"Input right:\t{R}\n")
L2, R2 = cipher.encrypt(L, R, k)
print(f"Encrypted (left): {L2}")
print(f"Encrypted (right): {R2}\n")
L, R = cipher.decrypt(L2, R2, k)
print("Output left:\t",L)
print("Output right:\t",R,"\n")
以及一个示例运行,其中包含 91075432 的密钥、21888242871839275222246405745257275088548364400416034343698204186575808495617 的素数、Lin=10654030123 和 Lout=10654030123 的 91 轮运行结果 [ 这里]:
Key: 91075432
Prime: 21888242871839275222246405745257275088548364400416034343698204186575808495617
Rounds: 91
Input left: 10654030123
Input right: 10654030123
Encrypted (left): 17627817925197112799945543966847828868819913020860563081515304827984756960523
Encrypted (right): 15425583952607434946356572183995490470776188183595688543699979320929622955821
Output left: 10654030123
Output right: 200750243212你可以在这里尝试:
F 上的 MiMC-Feistel(双分支 Feistel 网络)
参考文献
[1] Albrecht, M., Grassi, L., Rechberger, C., Roy, A., & Tiessen, T. (2016, November). MiMC: Efficient encryption and cryptographic hashing with minimal multiplicative complexity. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 191–219). Berlin, Heidelberg: Springer Berlin Heidelberg.
- 原文链接: billatnapier.medium.com/...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 165 浏览
- 以太坊协议研究学习小组 - 2026 启动 279 浏览
- 神奇的 Zig、C 和 OpenSSL 217 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 371 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 292 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 385 浏览
- Shamir份额的魔力:BLS门限签名 481 浏览
- Zcash:比特币遗忘的隐私 437 浏览
- ZK编年史:计算模型 306 浏览
- lambdaworks 2026 年更新路线图和优先级 375 浏览
- 2026年构建机构级DeFi平台真正需要什么 920 浏览
- zkMesh:2026年1月回顾 462 浏览

