冷密钥共享

Frosty Key Shares

在 LastingAsset，我们的目标是支持隐私感知的方法来存储个人详细信息，例如私钥、位置详细信息和受信任的电话号码。为此，我们可以将一个密钥拆分成多个密钥分片（secret shares），然后将它们存储在受信任的位置。这样，私钥就不会存在于任何单一位置，而只能从这些受信任的位置恢复。为此，我们可以采用全有或全无 (AoN) 的方法，在这种方法中，我们必须恢复密钥的所有分片才能重建它。但是，为了提高弹性，我们可以使用 Shamir 秘密共享 (SSS) 方法来支持任何 t-and-n 的共享方法。例如，我们可以将密钥分成五个片段，然后只需要组合三个片段即可恢复密钥。在本例中，我们将使用 FROST (Flexible Round-Optimised Schnorr Threshold) 方法将密钥分成多个分片，然后使用给定阈值数量的分片来恢复它。

Shamir Shares

现在，我们经常使用椭圆曲线在密码学中执行高效的运算。有了这个，我们从一个秘密 (s) 开始，然后取曲线的基点（G），并生成一个 sG 的秘密。接下来，我们将 sG 转换为给定阈值 t 和 n 个分片的多个多项式因子。首先，我们将取分片点，然后将其拆分为多个多项式值，并且我们切割 y 轴的点将恢复分片。最初，我们将使用以下公式将多项式拟合到秘密：

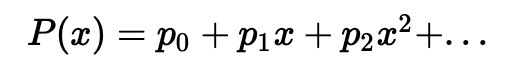
其中 p 0, p 1 等等，是所需多项式的系数。然后我们将创建 P(1), P(2) 等等的分片。这些是当 x =1, x =2 等等时的点。然后可以将这些分片分发给将存储这些分片的实体。当需要时，我们收集至少 t 个分片以重新创建秘密（ sG ）。例如，我们可以使用 P(0), P(1) … P( t −1) 并使用曲线拟合方法来找到 P(0)，它是多项式中 x =0 的点。然后将我们恢复的 P(0) 值转换回椭圆曲线点，以给出 sG ：

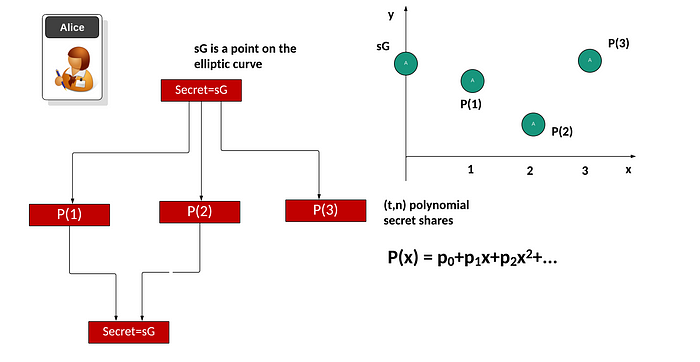
FROST

FROST 分布式签名 [2, 3] 方法允许阈值签名，其中任何 t 个中的 n 个都可以生成有效的签名。有了这个，我们将密钥分发给 n 个参与者，其中需要 t 个参与者来重新生成密钥并生成有效的签名。每个参与者都持有密钥的一个分片。总的来说，它只需要两轮来计算签名，并使用基于 Schnorr 的阈值签名方法。在本例中，我们将使用多种密码套件，包括 Ristretto255Sha512、P256Sha2562、P384Sha384、P521Sha512、Edwards25519Sha512 和 Secp256k1Sha256。EdDSA 签名是确定性的，但 FROST 签名是非确定性的 (因此每次我们创建签名时都会更改)。zCash 目前正在将 FROST 方法集成到他们的钱包中。

在本例中，我们将使用任意 3-from-5 的分片，然后使用分片 1、3 和 5 来重新生成密钥分片，然后根据公钥对其进行测试 [ here]:

// Code based on https://github.com/bytemare/dkg/tree/main
package main

import (
    "github.com/bytemare/ecc"
     "github.com/bytemare/dkg"
    "fmt"
 "github.com/bytemare/secret-sharing/keys"
 "slices"
 secretsharing "github.com/bytemare/secret-sharing"
 "os"
 "strconv"

)

var testTable = []*testCase{
 {
  name:            "Ristretto255 (3,5)",
  ciphersuite:     dkg.Ristretto255Sha512,
  group:           ecc.Ristretto255Sha512,
  threshold:       3,
  maxParticipants: 5,

 },
 {
  name:            "P-256 (3,5)",
  ciphersuite:     dkg.P256Sha256,
  group:           ecc.P256Sha256,
  threshold:       3,
  maxParticipants: 5,

 },
 {
  name:            "P-384 (3,5)",
  ciphersuite:     dkg.P384Sha384,
  group:           ecc.P384Sha384,
  threshold:       3,
  maxParticipants: 5,

 },
 {
  name:            "P-521 (3,5)",
  ciphersuite:     dkg.P521Sha512,
  group:           ecc.P521Sha512,
  threshold:       3,
  maxParticipants: 5,

 },
 {
  name:            "Edwards25519 (3,5)",
  ciphersuite:     dkg.Edwards25519Sha512,
  group:           ecc.Edwards25519Sha512,
  threshold:       3,
  maxParticipants: 5,

 },
 {
  name:            "SECp256k1 (3,5)",
  ciphersuite:     dkg.Secp256k1,
  group:           ecc.Secp256k1Sha256,
  threshold:       3,
  maxParticipants: 5,

 },
}

type testCase struct {
 name            string
 threshold       uint16
 maxParticipants uint16
 ciphersuite     dkg.Ciphersuite
 group           ecc.Group
}

func makeParticipants(c *testCase) []*dkg.Participant {
 ps := make([]*dkg.Participant, 0, c.maxParticipants)
 for i := range c.maxParticipants {
  p, err := c.ciphersuite.NewParticipant(i+1, c.threshold, c.maxParticipants)
  if err != nil {

  }

  ps = append(ps, p)
 }

 return ps
}

func runRound2(c *testCase, p []*dkg.Participant, r1 []*dkg.Round1Data) map[uint16][]*dkg.Round2Data {
 r2 := make(map[uint16][]*dkg.Round2Data, c.maxParticipants)
 for i := range c.maxParticipants {
  r, err := p[i].Continue(r1)
  if err != nil {

  }

  for id, data := range r {
   if r2[id] == nil {
    r2[id] = make([]*dkg.Round2Data, 0, c.maxParticipants-1)
   }
   r2[id] = append(r2[id], data)
  }
 }

 return r2
}

func showDetails(c *testCase,pk *ecc.Element,pubKey *ecc.Element,secret *ecc.Scalar, shares []*keys.KeyShare) {

 fmt.Printf("Participants: %d\n", c.maxParticipants)
 fmt.Printf("Threshold: %d\n", c.threshold)
 fmt.Printf("Name: %s\n", c.name)

 if (c.ciphersuite==1) { fmt.Printf("Ciphersuite: Ristretto255Sha512\n") }
 if (c.ciphersuite==3) { fmt.Printf("Ciphersuite: P256Sha2562\n") }
 if (c.ciphersuite==4) { fmt.Printf("Ciphersuite: P384Sha384\n") }
 if (c.ciphersuite==5) { fmt.Printf("Ciphersuite: P521Sha512\n") }
 if (c.ciphersuite==6) { fmt.Printf("Ciphersuite: Edwards25519Sha512\n") }
 if (c.ciphersuite==7) { fmt.Printf("Ciphersuite: Secp256k1Sha256\n") }
 fmt.Printf("Group: %v\n", c.group)

 fmt.Printf("\nRegenerated secret key %v\n", secret.Hex())

 fmt.Printf("Public key (initial gen) %v\n", pubKey.Hex())
 fmt.Printf("Public key (from shares) %v\n\n", pk.Hex())

 fmt.Printf("\nShares used:\n") // 使用的分片
 for _, k := range shares {
  fmt.Printf("Share: %v\n", k.Hex()) // 分片
 }

}

func main() {

 testvector:=0

    argCount := len(os.Args[1:])

        if (argCount>0) {testvector,_ = strconv.Atoi(os.Args[1])}

  c:= testTable[testvector]

  p := makeParticipants(c)
  r1 := make([]*dkg.Round1Data, c.maxParticipants)

  // Step 1: Start and assemble packages.
  for i := range c.maxParticipants {
   r1[i] = p[i].Start()
  }

  // Step 2: Continue and assemble + triage packages.
  r2 := runRound2(c, p, r1)

  // Step 3: Clean the proofs.
  // This must be called by each participant on their copy of the r1DataSet.
  for _, d := range r1 {
   d.ProofOfKnowledge.Clear()
  }

  // Step 4: Finalize

  quals := []uint16{1, 3, 5}

  keyShares := make([]*keys.KeyShare, 0, len(quals))

  registry := keys.NewPublicKeyShareRegistry(c.group, c.threshold, c.maxParticipants)
  pubKey, _ := dkg.VerificationKeyFromRound1(c.ciphersuite, r1)

  for _, participant := range p {
   keyShare, err := participant.Finalize(r1, r2[participant.Identifier])
   if err != nil {
    // t.Fatal(err)
   }

   if !keyShare.VerificationKey.Equal(pubKey) {
   // t.Fatalf("expected same public key")
   }

   if !keyShare.PublicKey.Equal(c.group.Base().Multiply(keyShare.Secret)) {
   // t.Fatal("expected equality")
   }

   if err := registry.Add(keyShare.Public()); err != nil {
   // t.Fatal(err)
   }

   // Assemble a subset to test key recovery.
   if slices.Contains(quals, participant.Identifier) { // only take the selected identifiers (1, 3 and 5)
    keyShares = append(keyShares, keyShare)
   }
  }

  {
   commitments := dkg.VSSCommitmentsFromRegistry(registry)
   for _, k := range keyShares {
    if err := dkg.VerifyPublicKey(c.ciphersuite, k.Identifier(), k.PublicKey, commitments); err != nil {
    // t.Fatal(err)
    }
   }
  }

  // Verify the threshold scheme by combining a subset of the shares.
  {
   combinedKeyShares  := make([]*keys.KeyShare, 0, len(quals))

   for _, k := range keyShares {
    combinedKeyShares = append(combinedKeyShares, k)
   }
   secret, err := secretsharing.CombineShares(combinedKeyShares)
   if err != nil {
   // fmt.Printf("\nUnsuccessfully combined shares\n")
   } else {
    fmt.Printf("\nSuccessfully combined shares\n") // 成功合并分片
   }

   pk := c.group.Base().Multiply(secret)
   if !pk.Equal(pubKey) {
   // fmt.Printf("Recovered secret not compatible with public key\n")
   } else {
    fmt.Printf("Recovered secret is compatible with public key\n") // 恢复的密钥与公钥兼容
   }

   showDetails(c,pk,pubKey,secret,keyShares )
  }
 }

一个示例运行 [ here]:

Successfully combined shares
Recovered secret is compatible with public key
Participants: 5
Threshold: 3
Name: Ristretto255 (3,5)
Ciphersuite: Ristretto255Sha512
Group: ristretto255_XMD:SHA-512_R255MAP_RO_

Regenerated secret key 82b27a7a6f19b941d168891d4e3d939aa1b4890b567f7038d66a23253a156c0a
Public key (initial gen) 7c2245a9059846a365506687380e63c21a46994e8ca41e0588b197b62b084f2f
Public key (from shares) 7c2245a9059846a365506687380e63c21a46994e8ca41e0588b197b62b084f2f

Shares used:
Share: 01010003000000ec00432795c49dd860fa5c85285ed1f3cd7ad4e756e64f7ed190ae73893d2d73587eb3ac3fdff241ffa7475c81455542f6868b2e3751e2eec9352decac85e45b6c29f9aad7603c1c28ddf80feeed52ec4e7c8427684f26e913ae64ffe830dc0b7a11d665735ccbad57c375f2a2b7ba45a969125ec96b8199cc38d20082b3b76366d2748e1c05ad62f43bc3b9b4a5c0d815e2c644752e90962a539c0a4c036e0e7c2245a9059846a365506687380e63c21a46994e8ca41e0588b197b62b084f2f
Share: 0103000300000008e6582d3e359e1c5efa2fe2a0fad7e71631c2e25ef4e5e8583f8e029f620f192694a21a756a9302842fe34fa3398ca9e1c51236e171aa514d32bf5d8d11b9660416b204f2c9ba07cef10205237c14ef766d6b7ed5b6c238558a904c03e1d8367e75a449caa3c0b4726dcdf50d96dba71ba609b1bb67672b9c72c0ab41128b66aec8bcefe05832d6f6a4f55bcb57c9dfb6e7cc1fbf8df99c298acfa2d66c68057c2245a9059846a365506687380e63c21a46994e8ca41e0588b197b62b084f2f
Share: 010500030000007637de1af3a7062ff6058cd2dcebbdf907f56b0c08a982ac19f4c5ffadc6862d92aee8a58297e2f6fb618d3617fe193ab0020f988b5ecfe0ea9ddf090de6ec6ccc70bf74e3fcf32b82a1e36c90f03c175adaf4ab52fe0d74940f072f62eafd2786c5a2e12fdaf85cfefd8b5919e379ec188e0938b728bd28d9f10769b5d8e05781130ee35ea2fd73596c18f0b6d682c2f8d037866dee9a5b46f459f7943d56007c2245a9059846a365506687380e63c21a46994e8ca41e0588b197b62b084f2f

结论

虽然有几种多重签名方法，但 FROST 是一种创建分布式签名的高效方法。它在加密货币中的应用是显而易见的，我们可以创建一个签名者组，并且我们需要至少给定数量的签名者才能完成交易。但是，还有更多的应用，包括创建一组受信任的设备，这些设备能够验证一个人或在密钥/ID 恢复中发挥作用。

参考文献

[1] Shamir, A. (1979). How to share a secret. Communications of the ACM, 22(11), 612–613 [ here].

[2] Komlo, C., & Goldberg, I. (2020, October). FROST: Flexible round-optimized Schnorr threshold signatures. In International Conference on Selected Areas in Cryptography (pp. 34–65). Cham: Springer International Publishing.

[3] Connolly, D., Komlo, C., Goldberg, I., & Wood, C. A. (2024). The Flexible Round-Optimized Schnorr Threshold (FROST) Protocol for Two-Round Schnorr Signatures. RFC 9591. June 2024. doi: 10.17487/RFC9591. url: https://www. rfc-editor. org/info/rfc9591.

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～