Baby Jubjub 椭圆曲线 与零知识证明

Baby Jubjub 与零知识证明

Baby Jubjub 是一种电子宠物，但它也是一种椭圆曲线，支持增强的零知识证明的使用

区块链技术的核心进步之一是零知识证明 (ZKP)，尤其是围绕 zk-SNARKs（零知识简洁非交互知识论证）。 通过这种方式，我们使用在有限域上定义的算术电路（zk-SNARK 电路）。 为了验证 zk-SNARK 证明，我们需要定义一条椭圆曲线。 对于以太坊，我们使用 BN254 曲线。 作为替代方案，我们可以使用 Baby Jubjub 曲线作为 zk-SNARK 电路，该电路支持一系列密码学原语，例如 Pedersen Hash 或 Edwards 数字签名算法 (EdDSA)。

为什么选择 Baby Jubjub？

创建 Baby Jubjub 是为了满足使用 F_r 算术电路的椭圆曲线的要求（其中我们有一个大小为 r 的有限域 (F_r)）。 选择扭曲 Edwards 曲线是因为它具有一个完整的公式，用于在曲线上添加两个点 - 这对于电路内的计算非常有效。 除此之外，扭曲的 Edwards 曲线可以转换为等效的 Montgomery 曲线。 这允许在电路外部的 Montgomery 曲线中进行点加法和倍乘 [here]：

总体而言，该设计是取素数 p = 1 (mod 4)，然后找到 A 的最低值，使得 A-2 是 4 的倍数。选择的素数是：

r =21888242871839275222246405745257275088548364400416034343698204186575808495617

这实际上是 BN128 的阶数（因此具有同等的安全级别）。 结果是：

a =168,700

d =168,696

设置

使用 Baby Jubjub 曲线，我们定义一个有限域（Fr），其中包含 r 个元素：

r =21888242871839275222246405745257275088548364400416034343698204186575808495617

然后，我们在 Fr 上使用扭曲的 Edwards 椭圆曲线（E(Fr）[here]：

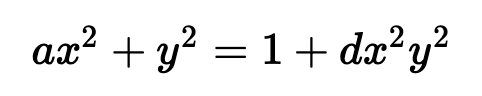
其中：

a =168700

d =168696

那么该曲线的阶数为：

n =21888242871839275222246405745257275088614511777268538073601725287587578984328

可以分解为：

n = h × l

在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的故事

免费加入 Medium 以获取此作者的更新。

并且 h 是协因子，l 是一个 251 位的素数：

h =8

l =2736030358979909402780800718157159386076813972158567259200215660948447373041

生成器点

然后我们可以使用生成器点来执行标量乘法。 在 Baby Jubjub 中，生成器点（G）是：

Gx =995203441582195749578291179787384436505546430278305826713579947235728471134

Gy =5472060717959818805561601436314318772137091100104008585924551046643952123905

在 Go 中，我们可以使用 Big Integers 来设置生成器点：

// The Generator Point (G)  // 生成器点 (G)
x,_ := new(big.Int).SetString("995203441582195749578291179787384436505546430278305826713579947235728471134",10 )
y,_ := new(big.Int).SetString("5472060717959818805561601436314318772137091100104008585924551046643952123905",10)
G := &babyjub.Point{X: x, Y: y}

点加

点的相加变得很简单：

P 1=(x 1, y 1)

P 2=(x 2, y 2)

我们可以计算：

P 3= P 1+ P 2

使用：

x 3=(x 1. y 2+ y 1. x 2)/(1+ d. x 1. x 2. y 1. y 2)

y 3=(y 1. y 2− a. x 1. x 2)/(1− d. x 1. x 2. y 1. y 2)

我们可以在同一函数中执行点加法（P 1+ P 2）和点倍乘（2. P 1）。

编码

在这种情况下，我们将定义一个标量值（s），然后创建一个点 sG，其中 G 是曲线上的生成器点 [here]：

package main
import (
 "math/big"
 "github.com/iden3/go-iden3-crypto/v2/babyjub"
 "fmt"
 "os"
)
func main() {
 scalar:="1"
 argCount := len(os.Args[1:])
 if (argCount>0) {scalar= string(os.Args[1])}

 // The Generator Point (G)  // 生成器点 (G)
 x,_ := new(big.Int).SetString("995203441582195749578291179787384436505546430278305826713579947235728471134",10 )
 y,_ := new(big.Int).SetString("5472060717959818805561601436314318772137091100104008585924551046643952123905",10)

 G := &babyjub.Point{X: x, Y: y}
 s, _ := new(big.Int).SetString(scalar,10)

 sG := babyjub.NewPoint().Mul(s, G)

 sGAdd := babyjub.NewPoint().Projective().Add(sG.Projective(),G.Projective())

 fmt.Printf("s: %s\n",s)
 fmt.Printf("G: (%s, %s) On Curve: %v\n",G.X.String(),G.Y.String(),G.InCurve())
 fmt.Printf("sG: (%s, %s) On Curve: %v\n",sG.X.String(),sG.Y.String(),sG.InCurve())
 fmt.Printf("G+sG: (%s, %s)\n",sGAdd.X.String(),sGAdd.Y.String())
}

一个使用 512. G 的示例运行位于 [here]：

s: 512
G: (995203441582195749578291179787384436505546430278305826713579947235728471134, 5472060717959818805561601436314318772137091100104008585924551046643952123905) On Curve: true
sG: (11147493790480072323687435957938716856159204975974571370488032222228450666507, 7297783963315293144303066632651031949682903221819939895220732712782447138294) On Curve: true
G+sG: (21014688584666710897531850558471088615250442167817061670140819536964746367061, 8310021433342935878374652965681433303324695761674219649367794271691384683528)

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～