哈希方法的构建者(以及更多)
- asecuritysite
- 发布于 2025-11-30 11:42
- 阅读 731
本文介绍了密码学专家Ivan Damgård在哈希方法、同态加密和多方安全协议等领域的贡献。重点介绍了他参与构建的Merkle-Damgård结构,该结构是MD5、SHA-1和SHA-2等哈希算法的基础,并探讨了Damgård-Jurik同态加密方法和Damgård-Fujisaki零知识证明方法。
哈希方法构建者(以及更多)
如果你从事网络安全工作,那么你就会了解 MD5 哈希方法。但是你知道 MD 部分代表什么吗? 嗯,它可能是消息摘要(Message Digest),但也可能是 Merkle-Damgård (MD) 结构,MD5、SHA-1 和 SHA-2 都是在此基础上构建的。 总的来说,Ivan Damgård 和 Ralph Merke 独立发现了它,并在 [1] 中发表:

所以,上周五,我很荣幸能与 Ivan Damgård 交谈:
2020 年,他因一篇题为“A Generalisation, a Simplification and Some Applications of Pallier's Probabilistic Public-Key System”的论文获得了时间考验奖[ 此处][3]:

2021 年,他因一篇题为“Multiparty unconditionally secure protocols”的论文获得 ACM 时间考验奖[ 此处][4]:

2010 年,他当选为国际密码学研究协会会员。Ivan 还是两家密码学公司 Cryptomathic 和 Partisia 的联合创始人。总的来说,他为网络安全的许多其他领域做出了贡献,所以让我们介绍几个[ 此处]。
Merkle-Damgård 结构:MD5、SHA-1 和 SHA-2
简单的数据哈希概念奠定了网络安全信任的基础,我们获取数据并为数据创建一个固定长度的哈希。如果我们不能信任我们的哈希方法,我们就麻烦了。当我们创建完美的 message hash 时,我们需要确保我们有:
- 抗碰撞性(Collision resistance)。 很难找到两个具有相同哈希的消息。因此,我们应该无法在合理的时间内找到两条消息(M1 和 M2)的相同哈希:H(M1)=H(M2)。
- 抗原像性(Pre-image resistance)。 如果我们已经有一个哈希值 ($h$),那么找到一个给出相同哈希的消息应该非常困难。因此,对于给定的哈希 ($h$),很难找到 H(M1)=$h$ 的消息 (M1)。
最初的哈希方法通常基于 Merkle-Damgård (MD) 结构。这样,我们使用数据块创建一个哈希函数。基于 MD 结构,Ron Rivest 创建了 MD5 哈希方法,并在业界得到广泛应用。它的工作原理是采用静态初始化向量 (IV),然后将其输入到单向函数 ($f$) 中,以及消息块。我们将这个输出输入到下一阶段,依此类推,直到我们到达末尾的消息填充:
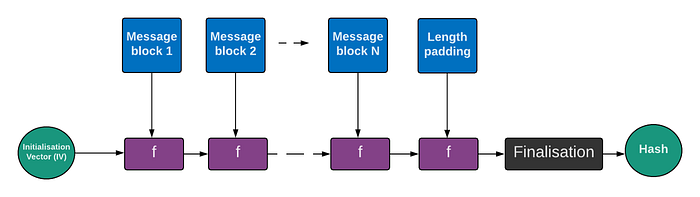
单向函数 ($f$) 通常会压缩数据,并产生比输入更少的比特。不幸的是,MD 结构有很多弱点,其中最严重的一个是长度扩展攻击。这样,对手 (Eve) 可以获取未知消息的哈希,然后添加额外的数据来生成新的有效哈希。如果你有兴趣,这里有一个针对 MD 的攻击:
https://asecuritysite.com/hash/lenattack
Damgård-Jurik 方法
网络安全领域两个主要发展领域将是同态加密的使用和 Shamir 秘密共享的使用。使用同态加密,我们可以加密值,然后使用算术函数(例如加、减和乘)对它们进行运算,使用 Shamir 秘密共享,我们可以将秘密分成若干 shares,然后在网路上传输它们。 这些方法将把隐私提升到新的水平。所以,让我们看看 Damgård-Jurik 方法 [2]:

首先,我们选择两个大素数 ($p$ 和 $q$) 并计算:
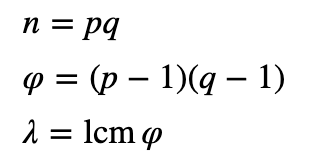
其中 lcm 是最小公倍数。然后我们为以下内容选择随机整数 $g$:
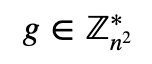
我们必须通过检查以下内容来确保 $n$ 除 $g$ 的阶:
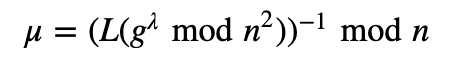
其中 $L$ 定义为 $L(x) = \frac{x − 1}{n}$。公钥是 ($n$, $g$),私钥是 ($λ$, $μ$)。要加密消息 ($M$),我们选择一个随机 $r$ 值并计算密文:
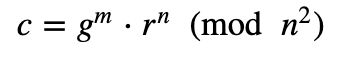
然后解密:
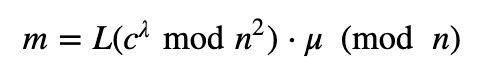
如果我们取两个密码 ($C_1$ 和 $C_2$),我们得到:
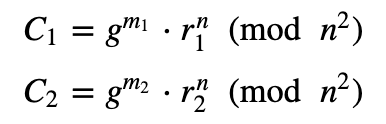
如果我们将它们相乘,我们会得到:
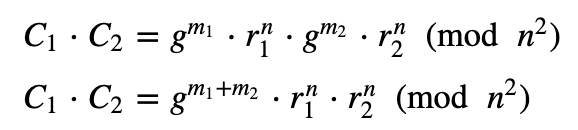
因此,添加两个值需要密码的乘法。如果我们将它们分开,我们会得到:
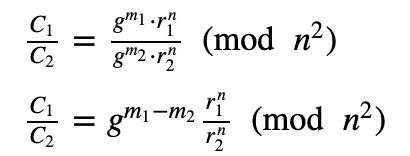
因此,减法相当于除法运算。为此,我们执行模除运算。编码是 [ 此处]:
from damgard_jurik import keygen
import sys
val_1, val_2 = 42, 12
n_b=64
if (len(sys.argv)>1):
val_1=int(sys.argv[1])
if (len(sys.argv)>2):
val_2=int(sys.argv[2])
if (len(sys.argv)>3):
n_b=int(sys.argv[3])
public_key, private_key_ring = keygen(
n_bits=n_b,
s=1,
threshold=3,
n_shares=3
)
print(f"Using Damgard-Jurik method with {n_b}-bit key, and a threshold of three and three shares\n") # 使用具有 {n_b} 位密钥的 Damgard-Jurik 方法,阈值为三和三个 shares
print(f"Public key. n={public_key.n}, s={public_key.s}, m={public_key.m}, threshold={public_key.threshold}, delta={public_key.delta}") # 公钥。 n={public_key.n}, s={public_key.s}, m={public_key.m}, 阈值={public_key.threshold}, delta={public_key.delta}
c_1, c_2 = public_key.encrypt(val_1), public_key.encrypt(val_2)
c_add = c_1 + c_2
res1 = private_key_ring.decrypt(c_add)
c_sub = c_1 - c_2
res2 = private_key_ring.decrypt(c_sub)
c_mult= c_1 * val_2
res3 = private_key_ring.decrypt(c_mult)
print(f"\nval_1: {val_1}")
print(f"val_2: {val_2}")
print(f"\nc_1: {c_1.value}")
print(f"c_2: {c_2.value}")
print(f"c_1+c_2: {c_add.value}")
print(f"c_1-c_2: {c_sub.value}")
print(f"c_1*c_2: {c_mult.value}")
print(f"\nDecrypt (Add): {res1}") # 解密(加法)
print(f"Decrypt (Subtract): {res2}") # 解密(减法)
print(f"Decrypt (Multiply): {res3}") # 解密(乘法)一个示例运行是 [ 此处]:
Using Damgard-Jurik method with 64-bit key, and a threshold of three and three shares
Public key. n=174743826971117924232203186477859825289, s=1, m=43685956742779481051423225748488060689, threshold=3, delta=6
val_1: 9
val_2: 3
c_1: 27429320619805987848765352451564237217145248338366944942206061954884249278992
c_2: 14769913771126168413630660895236067257037103416139804498830583273184880216135
c_1+c_2: 12086035254029813325315665006256800980915988130367594983597188460984693331181
c_1-c_2: 921687804424968958981627966721274246800285129994018401822135562246021703624
c_1*c_2: 21809874053261031282086634289802837387921962314468453992976726818561314427636
Decrypt (Add): 12
Decrypt (Subtract): 6
Decrypt (Multiply): 27关于“A Generalisation, a Simplification and Some Applications of Paillier’s Probabilistic Public-Key System”的研究获得了 PKC 2001 的时间考验奖。
Damgård-Fujisaki 方法
使用 Damgård-Fujisaki 方法,Peggy 向 Victor 证明她具有正整数值。在这种情况下,我们将使用 [ 此处]定义的 Damgard-Fujisaki 方法,其中 Peggy 必须向 Victor 证明她有一个正值:

首先,Victor 和 Peggy 就他们计算的两个基数 ($g$ 和 $h$) 和一个素数 ($n$) 达成一致。然后,Victor 使用随机数 ($r$) 作为挑战发送给 Peggy。正如 Jacobi 的四平方定理所定义的那样,每个正值都可以表示为以下形式:
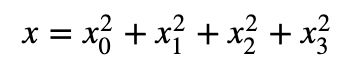
例如:
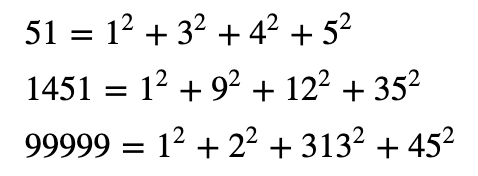
Peggy 现在从这四个值创建四个承诺,并获得四个随机数 ($r_0$, $r_1$, $r_2$ 和 $r_3$)。
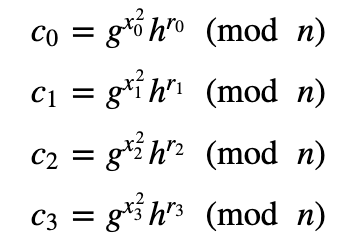
并且:
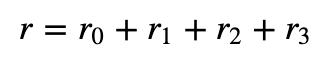
然后 Victor 检查:
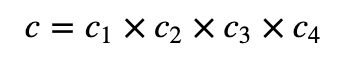
这应该等于:
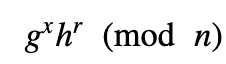
以下是一些简单的编码来证明该方法。 在这种情况下,我们将使用 2¹⁹−1 的素数,$g$ =3 且 $h$ =5 [ 此处]:
import random
import sys
n=pow(2,19)-1
def lipmaa(val):
for i in range(0,100000):
for j in range(0,1000):
for k in range(0,100):
for l in range(0,10):
if (((i*i) + (j*j) + (k*k) + (l*l)) == val): return (i,j,k,l)
return(0)
x=999909
if (len(sys.argv)>1):
x=int(sys.argv[1])
if (x<0): print("Not possible to find a commitment, as negative") # 如果为负数,则无法找到承诺
sys.exit(1)
x0,x1,x2,x3=lipmaa(x)
print ("x=",x)
print (" x0,x1,x2,x3=",x0,x1, x2,x3)
g=3
h=4
r0=random.randint(0,n)
r1=random.randint(0,n)
r2=random.randint(0,n)
r3=random.randint(0,n)
r=(r0+r1+r2+r3)
c0=(pow(g,x0*x0,n) * pow(h,r0,n)) % n
print (" \nc0=",c0)
c1=(pow(g,x1*x1,n) * pow(h,r1,n)) % n
print (" c1=",c1)
c2=(pow(g,x2*x2,n) * pow(h,r2,n)) % n
print (" c2=",c2)
c3=(pow(g,x3*x3,n) * pow(h,r3,n)) % n
print (" c3=",c3)
commit1 = (c0*c1*c2*c3) % n
print (" \nCheck1=",commit1)
commit2 = (pow(g,x,n) * pow(h,r,n)) % n
print (" Check2=",commit2)
if (commit1==commit2):
print(" Peggy has proven that her value is positive") # Peggy 已经证明她的价值是正的作为一个测试:
x= 70
x0,x1,x2,x3= 0 3 5 6
c0= 131072
c1= 422276
c2= 216515
c3= 179023
Check1= 482996
Check2= 482996
Peggy has proven that her value is positive这是一个范围证明:
https://asecuritysite.com/kryptology/z_df5
结论
丹麦人对科学和数学的热爱是有原因的……并且可能永远如此。 Ivan 是一位杰出的研究员,他奠定了哈希的核心原则,并且在过去的二十年中,他继续为许多新方法做出了贡献。
参考文献
[1] Damgård, I. B. (1989, August). A design principle for hash functions. In Conference on the Theory and Application of Cryptology (pp. 416–427). New York, NY: Springer New York.
[2] Damgård, I., Jurik, M., & Nielsen, J. B. (2010). A generalization of Paillier’s public-key system with applications to electronic voting. International Journal of Information Security, 9(6), 371–385.
[3] Damgård, I., & Jurik, M. (2001). A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In Public Key Cryptography: 4th International Workshop on Practice and Theory in Public Key Cryptosystems, PKC 2001 Cheju Island, Korea, February 13–15, 2001 Proceedings 4 (pp. 119–136). Springer Berlin Heidelberg.
[4] Chaum, D., Crépeau, C., & Damgard, I. (1988, January). Multiparty unconditionally secure protocols. In Proceedings of the twentieth annual ACM symposium on Theory of computing (pp. 11–19).
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 21
- 分类: 密码学
- 标签: Merkle-Damgård结构 MD5 SHA-1 SHA-2 同态加密 Damgård-Jurik 零知识证明 Damgård-Fujisaki
- ZK编年史:哈希登场 130 浏览
- 神奇的 Zig、C 和 OpenSSL 193 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 348 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 279 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 362 浏览
- Zcash:比特币遗忘的隐私 429 浏览
- ZK编年史:计算模型 296 浏览
- lambdaworks 2026 年更新路线图和优先级 360 浏览
- 2026年构建机构级DeFi平台真正需要什么 893 浏览
- zkMesh:2026年1月回顾 447 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 640 浏览
- Zcash 的时代到来了 768 浏览

