[ELIP-002]:Slashing升级对Staker和Operator份额会计的影响
- Layr-Labs
- 发布于 2025-02-14 13:20
- 阅读 862
本文档详细描述了Slashing Upgrade对Staker和Operator Shares会计的影响。
份额计算
本文档概述了由于 Slashing 升级而对 staker 和 operator 的份额计算所做的更改。引入了几个变量,例如存款缩放因子($k_n$),最大幅度($m_n$)和信标链削减因子($l_n$)。这些变量如何与 operator 和 staker 事件(如存款、削减、提款)相互作用将在下面进行描述。
预读
Slashing 升级前
我们将研究在 Slashing 升级之前历史定义的“份额”模型。在 Slashing 之前,staker 可以收到存入资产的份额,将这些份额委托给 operator,并从协议中提取这些份额。我们可以更正式地写成:
Staker 级别
$s_n$ - n 时刻 StrategyManager/EigenPodManager 存储中的份额数量。
Operator 级别
$op_n$ - n 时刻 DelegationManager 存储中的 operator 份额,也可以重写为 \
$opn = \sum{i=1}^{k} s_{n,i}$,其中 operator 有 $k$ 个委托给他们的 staker。
Staker 存款
在 n 时刻,每当 staker 存入金额 $d_n$ 时,staker 的份额和委托的 operator 的份额将按如下方式更新:
$$ s{n+1} = s{n} + d_{n} $$
$$ op{n+1} = op{n} + d_{n} $$
Staker 提款
同样,对于 staker 提款,给定在 n 时刻要提取的金额 $w_n$,staker 和 operator 的份额会在提款排队时减少:
$$ s{n+1} = s{n} - w_{n} $$
$$ op{n+1} = op{n} - w_{n} $$
之后,在提款延迟时间过去后,staker 可以完成他们的提款,以提取全部份额 $w_n$。
Slashing 升级变更
本文档的其余部分将假定理解 ELIP-002 中描述的分配/解除分配、最大幅度和 Operator 集。
术语
EigenLayer 中的“份额”一词历来指的是 staker 通过 StrategyManager 或 EigenPodManager 存入资产后收到的份额数量。除了 StrategyManager 中用于解释 rebase 代币的一些转换比率外,份额与存款金额大致呈 1:1 对应关系(即,beaconChainETHStrategy 中的 1e18 份额对应于 1 ETH 的资产)。当委托给 operator 或将提款排队时,DelegationManager 会从 StrategyManager 或 EigenPodManager 读取存款份额,以确定要委托(或取消委托)多少份额。
随着 Slashing 版本的发布,需要区分“类别”的份额。
存款份额:
以前称为“份额”,这些是 Slashing 版本之前使用的相同份额。它们继续由 StrategyManager 和 EigenPodManager 管理,并且与存入的资产大致呈 1:1 对应关系。
可提取份额:
当 operator 被 Slashing 时,Slashing 会异步应用于他们的 staker(否则,Slashing 将需要迭代每个 operator 的 staker;这是非常昂贵的)。
DelegationManager 必须找到许多 staker 的存款份额的通用表示形式,每个 staker 可能根据他们委托给哪个 operator 以及何时委托而经历了不同数量的 Slashing。这种通用表示部分通过称为 depositScalingFactor 的值来实现:这是一个每个 staker、每个策略的值,用于随着时间的推移缩放 staker 存入资产的存款份额。
当 staker 执行几乎任何操作(更改其委托的 operator、排队/完成提款、存入新资产)时,DelegationManager 会通过应用 staker 的 depositScalingFactor 和当前的Slashing 因子(主要从 AllocationManager 中 operator 收到的 Slashing 量得出的每个策略的标量)将他们的存款份额转换为可提取份额。
这些可提取份额用于确定 staker 的多少存款份额实际上能够从协议中提取,以及可以将多少份额委托给 operator。单个 staker 的可提取份额不会反映在任何存储中;它们是按需计算的。
Operator 份额:
Operator 份额是可提取份额的衍生品。当 staker 委托给 operator 时,他们正在委托他们的可提取份额。因此,operator 的 Operator 份额代表了他们所有 staker 的可提取份额的总和。请注意,当 staker 首次委托给 operator 时,这是一个特殊情况,其中存款份额 == 可提取份额。如果 staker 以后存入其他资产,如果在过渡期间经历了 Slashing,则此情况将不成立。
这些定义中的每一个也可以应用于 Slashing 前的份额模型,但需要注意的是,对于所有 staker,可提取份额等于存款份额。在 Slashing 升级之后,情况不一定如此 - 如果他们的 operator 遭到 Slashing,staker 可能无法提取他们存入的金额。
现在,让我们详细了解这些更新的定义,以及会计数学如何在存款、提款和 Slashing 中发挥作用。
存储变量
请注意,这些变量都在单个策略的上下文中定义。另请注意,这些等式中使用的“1”的概念在代码中由常量 1 WAD 或 1e18 表示。
Staker 级别
$s_n$ - n 时刻 StrategyManager/EigenPodManager 存储中的存款份额数量。在存储中:StrategyManager.stakerDepositShares 和 EigenPodManager.podOwnerDepositShares
$k_n$ - staker 在 n 时刻的“存款缩放因子”。这被初始化为 1。在存储中:DelegationManager.depositScalingFactor
$l_n$ - staker 在 n 时刻的“信标链削减因子”。这被初始化为 1。对于任何与非原生 ETH 策略相关的方程式,可以假定为 1。在存储中:EigenPodManager.beaconChainSlashingFactor
Operator 级别
$m_n$ - n 时刻的 operator 幅度。这被初始化为 1。
$op_n$ - n 时刻 DelegationManager 存储中的 operator 份额。在存储中:DelegationManager.operatorShares
概念变量
$a_n = s_n k_n l_n m_n$ - staker 在 n 时刻拥有的可提取份额。从视图函数 DelegationManager.getWithdrawableShares 读取
请注意,$opn = \sum{i=1}^{k} a_{n,i}$。
存款
对于新存入的份额金额 $d_n$,
Staker 级别
从概念上讲,staker 的存款份额和可提取份额都增加了存入的金额 $d_n$。让我们计算一下这种数学运算如何影响存款缩放因子 $k_n$。
$$ a_{n+1} = a_n + d_n $$
$$ s_{n+1} = s_n +d_n $$
$$ l_{n+1} = l_n $$
$$ m_{n+1} = m_n $$
展开 $a_{n+1}$ 计算
$$ s{n+1} k{n+1} l{n+1} m{n+1} = s_n k_n l_n m_n + d_n $$
简化产生:
$$ k_{n+1} = \frac{s_n k_n l_n m_n + dn}{s{n+1} l{n+1} m{n+1}}=\frac{s_n k_n l_n m_n + d_n}{(s_n+d_n)l_nm_n} $$
Slashing 因子的更新在 SlashingLib.update 中实现。
Operator 级别
对于 operator(如果 staker 已委托),委托的 operator 份额应增加与 staker 刚刚存入的完全相同的金额。因此,$op_n$ 的更新如下:
$$ op_{n+1} = op_n+d_n $$
请参阅以下实现:
委托
假设我们有一个未委托的 staker,他决定委托给 operator。 我们应保留以下属性。
Operator 级别
Operator 份额应增加 staker 拥有的可委托份额的数量,这与其可提取份额 $a_n$ 同义。因此,
$$ op{n+1} = op{n} + a_n $$
$$ = op_{n} + s_n k_n l_n m_n $$
Staker 级别
可提取份额应保持不变
$$ a_{n+1} = a_n $$
存款份额应保持不变
$$ s_{n+1} = s_n $$
beaconChainSlashingFactor 和 maxMagnitude 也应保持不变。在这种情况下,由于 staker 未被委托,因此其 maxMagnitude 默认应等于 1。
$$ l_{n+1} = l_n $$
现在的问题是,新的 depositScalingFactor 等于什么?
$$ a_{n+1} = a_n $$
$$ => s{n+1} k{n+1} l{n+1} m{n+1} = s_n k_n l_n m_n $$
$$ => s{n} k{n+1} l{n} m{n+1} = s_n k_n l_n m_n $$
$$ => k_{n+1} = \frac {k_n mn} { m{n+1} } $$
请注意,更新 $k{n+1}$ 和 $m{n+1}$ 的 staker 变量不会影响先前排队的提款和提款完成时收到的份额。这是因为查找的最大幅度取决于排队提款时的 operator,$k_n$ 有效地存储在缩放份额字段中。
Slashing
给定一个 Slashing 比例 $pn = \frac {m{n+1}}{m_n}$,
Operator 级别
从概念层面讲,operator 的份额应按以下比例减少:
$$ op_{n+1} = op_n p_n $$
$$ => op_{n+1} = opn \frac {m{n+1}} {m_n} $$
计算 $sharesToDecrement$ 的数量:
$$ sharesToDecrement = opn - op{n+1} $$
$$ = op_n - opn \frac {m{n+1}} {m_n} $$
此计算在 SlashingLib.calcSlashedAmount 中执行。
Staker 级别
从概念层面讲,staker 的可提取份额也应按比例减少,因此以下条件必须为真:
$$ a_{n+1} = a_n p_n $$
我们不想在 Slashing 期间更新 staker 级别的存储,因为考虑到 operator 与其委托的 staker 之间存在 1 对多的关系,这将使计算成本过高。因此,我们要证明 $a_{n+1} = a_n p_n$,因为可提取份额减少了 $p_n$。
给定以下内容:
$l_{n+1} = ln$ \ $k{n+1} = kn$ \ $s{n+1} = s_n$
展开 $a_{n+1}$ 方程:
$$ a{n+1} = s{n+1} k{n+1} l{n+1} m_{n+1} $$
$$ => s{n} k{n} l{n} m{n+1} $$
我们知道 $pn = \frac {m{n+1}}{mn}$ => $m{n+1} = m_n p_n$
$$ => s_n k_n l_n m_n p_n $$
$$ => a_n p_n $$
这意味着,一旦通过 Slashing 减少了其 operator 的 maxMagnitude,staker 的可提取份额就会立即受到影响。
排队提款
通过输入 depositShares 金额 $x_n <= s_n$ 来排队提款。与 $x_n$ 对应的实际可提取金额 $w_n$ 由以下公式给出:
$$ w_n = x_n k_n l_n m_n $$
从概念上讲,这是有道理的,因为要提取的金额 $w_n$ 是一些数量 <= $a_n$,这是 staker 的总可提取份额金额。
Operator 级别
当 staker 排队提款时,其 operator 的份额会相应减少:
$$ op_{n+1} = op_n - w_n $$
Staker 级别
$$ a_{n+1} = a_n - w_n $$
$$ s_{n+1} = s_n - x_n $$
这意味着,当排队提款时,staker 会输入一个 depositShares 金额 $x_n$。DelegationManager 调用 EigenPodManager/StrategyManager 以将他们的 depositShares 减少此金额。此外,depositShares 将转换为可提取金额 $w_n$,该金额将从 operator 的份额中减少。
我们希望表明,staker 的总可提取份额会相应减少,以使 $a_{n+1} = a_n - w_n$。
给定以下内容:
$l_{n+1} = ln$ \ $k{n+1} = kn$ \ $s{n+1} = s_n$
展开 $a_{n+1}$ 方程:
$$ a{n+1} = s{n+1} k{n+1} l{n+1} m_{n+1} $$
$$ => (s_{n} - xn) k{n+1} l{n+1} m{n+1} $$
$$ = (s_{n} - x_n) k_n l_n m_n $$
$$ = s_n k_n l_n m_n - x_n k_n l_n m_n $$
$$ = a_n - w_n $$
请注意,当提款排队时,会创建一个带有缩放份额的 Withdrawal 结构,定义为 $q_t = x_t k_t$,其中 $t$ 是排队的时间。完成提款 中将更清楚地说明我们像这样定义和存储缩放份额的原因。
此外,当用户排队提取其所有份额的提款时,我们会重置 depositScalingFactor,无论是通过取消/重新委托还是直接方式。这是因为提款时的 DSF 存储在缩放份额中,并且 staker 的任何“新”存款或委托都应被视为新的。请注意,当以份额形式完成提款时,它被视为一种存款,这在下面也会更清楚。
请参阅以下实现:
DelegationManager.queueWithdrawalsSlashingLib.scaleForQueueWithdrawal
<br>
完成提款
现在,staker 完成在时间 $t$ 排队的提款 $(q_t, t)$。
Operator 级别
如果 staker以代币形式完成提款,则任何 operator 份额都将保持不变。最初的 operator 的份额在提款排队时减少,如果 staker 提取资产(“以代币形式”),则新的 operator 不会收到份额。
但是,如果 staker以份额形式完成提款,则根据存款中的公式,份额将添加到 staker 当前的 operator 中。
Staker 级别
<!-- 除了需要计算发送给 staker 的份额之外,没有对 staker 进行存储更新。 -->
回想一下排队提款,当提款排队时,Withdrawal 结构体存储缩放份额,定义为 $q_t = x_t k_t$,其中 $x_t$ 是请求提款的存款份额金额,$t$ 是排队的时间。
并且,鉴于用于计算可提取份额的公式,给予 staker 的可提取份额为 $w_t$:
$$ w_t = q_t m_t l_t = x_t k_t l_t m_t $$
但是,staker 提款中的份额可能在提款排队期间已被 Slashing。他们的 operator 可能已被 AVS Slashing,或者,如果该策略是 beaconChainETHStrategy,则 staker 的验证器可能已被 Slashing/惩罚。
他们实际收到的份额数量按以下比例计算:
$$ \frac{m{t+delay} l{now} }{m_t l_t} $$
因此,完成时提取的实际份额金额计算为:
$$ sharesWithdrawn = wt (\frac{m{t+delay} l_{now}}{m_t l_t} ) $$
$$ = x_t k_t l_t mt (\frac{m{t+delay} l_{now}}{m_t l_t} ) $$
$$ = x_t kt m{t+delay} l_{now} $$
现在我们知道 $q_t = x_t k_t$,因此我们可以在此处替换此值。
$$ = qt m{t+delay} l_{now} $$
从上面的等式中,我们在排队提款时拥有的已知值是 $x_t kt$,而我们仅在可完成排队的提款时才知道 $m{t+delay} l_{now}$。这就是为什么我们将缩放份额存储为 $q_t = x_t kt$ 的原因。另一个术语($m{t+delay} l_{now}$)在提款完成交易期间读取。
注意:读取 $m{t+delay}$ 是通过 AllocationManager 中最大幅度的历史快照查找来执行的,而当前信标链 Slashing 因子 $l{now}$ 是通过 EigenPodManager 完成的。回想一下,如果所讨论的策略不是 beaconChainETHStrategy,$l_{now}$ 将默认为“1”。
缩放份额的定义仅用于处理提款和计算在排队期间可能发生的 Slashing(包括在 EigenLayer 和信标链上)。
请参阅以下实现:
DelegationManager.completeQueuedWithdrawalSlashingLib.scaleForCompleteWithdrawal
处理 EigenPod 中的信标链余额减少
引入信标链 Slashing 因子 $l_n$ 后,信标链余额减少的处理方式有所不同。
在升级之前,由于完成检查点而导致 staker 的 EigenPod 余额减少的任何金额都会立即从 EigenPodManager 中 staker 的份额中减少。作为一种极端情况,这意味着,例如,如果 staker 排队提取了所有份额,然后在他们的 EigenPod 上完成了一个显示余额减少的检查点,则 staker 的份额可能会变为负数。
随着信标链 Slashing 因子的引入,信标链余额的减少不再导致存款份额的减少。相反,staker 的信标链 Slashing 因子会减少,从而允许系统在任何现有份额以及任何现有排队的提款中实现该 Slashing。实际上,这意味着信标链 Slashing 的计算方式与 EigenLayer 本机 Slashing 类似;存款份额保持不变,而可提取份额减少:
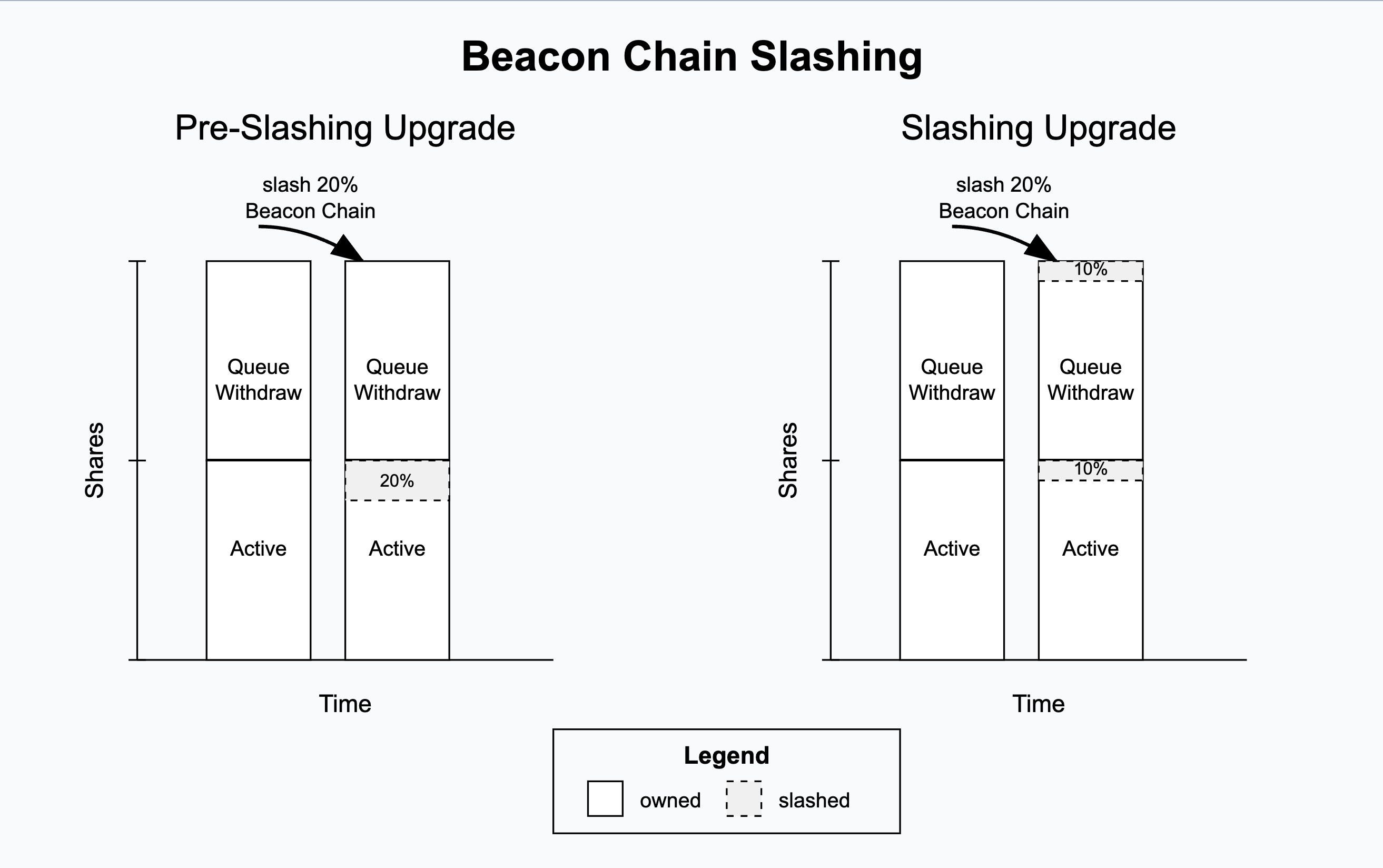
现在,让我们考虑一下,当信标链余额减少代表 staker 的 EigenPod 的负份额增量时,如何处理这些减少。
添加的定义
$welw$ 是 withdrawableExecutionLayerGwei。这纯粹是 EigenPod 中的本机 ETH,通过检查点进行归属,并被 pod 视为可提取(但未考虑任何 EigenLayer 本机 Slashing)。可以调用 DelegationManager.getWithdrawableShares 来同时考虑 EigenLayer 和信标链 Slashing。
$before\text{ }start$ 是刚好在检查点开始之前的时间
<!-- $before\text{ }complete$ 是刚好在检查点完成之前的时间 -->
$after\text{ }complete$ 是刚好在检查点完成之后的时间
完成检查点后,pod 的本机 ETH 和信标链余额之前和之后代表的总资产由以下公式给出:
$gn = welw{before\text{ }start}+\sum_i validatori.balance{before\text{ }start}$ \ $hn = welw{after\text{ }complete}+\sum_i validatori.balance{after\text{ }complete}$
Staker 级别
从概念上讲,以上逻辑指定我们按与余额减少成比例的方式减少 staker 的可提取份额:
$$ a_{n+1} = \frac{h_n}{g_n}a_n $$
我们通过设置来实现此目的
$$ l_{n+1}=\frac{h_n}{g_n}l_n $$
给定:
$m_{n+1}=mn$ (staker 信标链 Slashing 不会影响其 operator 的幅度) $s{n+1} = sn$ (不减少存款份额) $k{n+1}=k_n$
然后,将其插入可提取份额的公式中:
$$ a{n+1} = s{n+1}k{n+1}l{n+1}m_{n+1} $$
$$ =s_nk_n\frac{h_n}{g_n}l_nm_n $$
$$ = \frac{h_n}{g_n}a_n $$
Operator 级别
现在我们要相应地更新 operator 的份额。从概念上讲,$op_{n+1}$ 应该如下:
$$ op_{n+1} = op_n - an + a{n+1} $$
我们可以进一步简化它
$$ =op_{n}-s_nk_nl_nm_n + s_nknl{n+1}m_n $$
$$ = op_{n}+s_nk_nmn(l{n+1}-l_n) $$
请参阅以下实现:
EigenPodManager.recordBeaconChainETHBalanceUpdateDelegationManager.decreaseDelegatedShares
实施细节
实际上,我们实际上不能有浮点值,因此我们将用 $m_n$/1e18 $\frac{k_n}{1e18},\frac{l_n}{1e18} ,\frac{m_n}{1e18}$ 分别替换所有 $k_n, l_n, m_n$ 项,其中 $k_n, l_n, m_n$ 是存储中的值,全部初始化为 1e18。这使我们可以在概念上具有 $[0,1]$ 范围内的值。
我们利用 OpenZeppelin 的 Math 库和 mulDiv 以全精度计算 $floor(\frac{x \cdot y}{denominator})$。有时,对于特定的舍入极端情况,会显式使用 $ceiling(\frac{x \cdot y}{denominator})$。
乘法和除法运算
对于上述文档中的所有方程式,我们将 $k_n、l_n、m_n$ 的任何乘积运算替换为 mulWad 纯函数。
function mulWad(uint256 x, uint256 y) internal pure returns (uint256) {
return x.mulDiv(y, WAD);
}相反,对于 $k_n、l_n、m_n$ 的任何除法,我们使用 divWad 纯函数。
function divWad(uint256 x, uint256 y) internal pure returns (uint256) {
return x.mulDiv(WAD, y);
}
- 原文链接: github.com/Layr-Labs/eig...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 0
- 分类: 以太坊
- 标签: EigenLayer Slashing Upgrade Shares会计 存款比例因子 信标链削减因子 withdrawlable shares
- EigenCloud:寻找真正属于自己的东西 456 浏览
- 智能合约审计 vs DeFi 保险:2026 年你需要哪个? 495 浏览
- 第12章:再质押(Restaking) 1895 浏览
- 关于Restaking 发生了什么? 761 浏览
- 055:再质押经济的演化与风险扩散 1424 浏览
- EigenLayer:ETH 重新质押及其运作方式 546 浏览
- 047:再质押生态:EigenLayer 与信任复用 1598 浏览
- 可验证的云:EigenCloud如何开启加密应用和AI时代 2251 浏览
- 037:Restaking & EigenLayer:二次质押是什么? 1635 浏览
- EigenLayer 奖励计算 - 基础激励 1317 浏览
- ELIP-006 提议: 在 EigenLayer 中引入可重新分配的罚没机制 1190 浏览
- 流动性再质押代币(LRT)深度研究系列:第四部分 - LRT 的未来趋势与代币经济学 1899 浏览

