ZK数学详解：理解椭圆曲线
- Cyfrin
- 发布于 2025-08-29 19:53
- 阅读 14
本文深入探讨了椭圆曲线的数学结构、性质以及点加运算，并阐述了它们在密码学和零知识证明中的应用。文章介绍了椭圆曲线的定义、群的性质、点加法的几何规则以及射影坐标系中的无穷远点，为读者理解基于椭圆曲线的密码学原理及零知识证明技术奠定了基础。
ZK 数学 101：理解椭圆曲线
椭圆曲线是代数曲线，常用于密码学。深入探讨它们的技术原理，它们的结构、属性、点加法以及在 ZKP 中的应用。
椭圆曲线是一类代数曲线，经常用于密码学，最著名的是椭圆曲线数字签名算法 (ECDSA)和一些基于 SNARK 的零知识证明 (ZKP)，例如 PLONK。但它们是什么，它们如何工作，以及为什么使用它们？
本文提供了对椭圆曲线、它们的数学结构、属性、椭圆曲线点加法以及它们在密码学和 ZKP 中的应用的技术探索。
请注意，此资源旨在帮助程序员熟悉理解密码学和零知识证明的数学先决条件。为了简洁起见，省略了数学推导，但会链接资源，供那些希望进一步理解的人使用。
什么是椭圆曲线？
椭圆曲线是一类代数曲线，其方程形式为：
y2=x3+ax+b
其中 a 和 b 是常数系数。曲线必须在域 K 上定义，这意味着坐标 (x,y) 和系数 (a,b) 必须都是域 K 的元素。
这是最常见的椭圆曲线方程形式，称为 affine（仿射） Weierstrass（维尔斯特拉斯） 形式。其他形式包括 twisted Edwards（扭曲爱德华兹）形式 和 Montgomery（蒙哥马利）形式，本文将不介绍这些形式。
在下面的图 1 中，你可以看到在实数域上定义的椭圆曲线，其中 a=−1 和 b=1
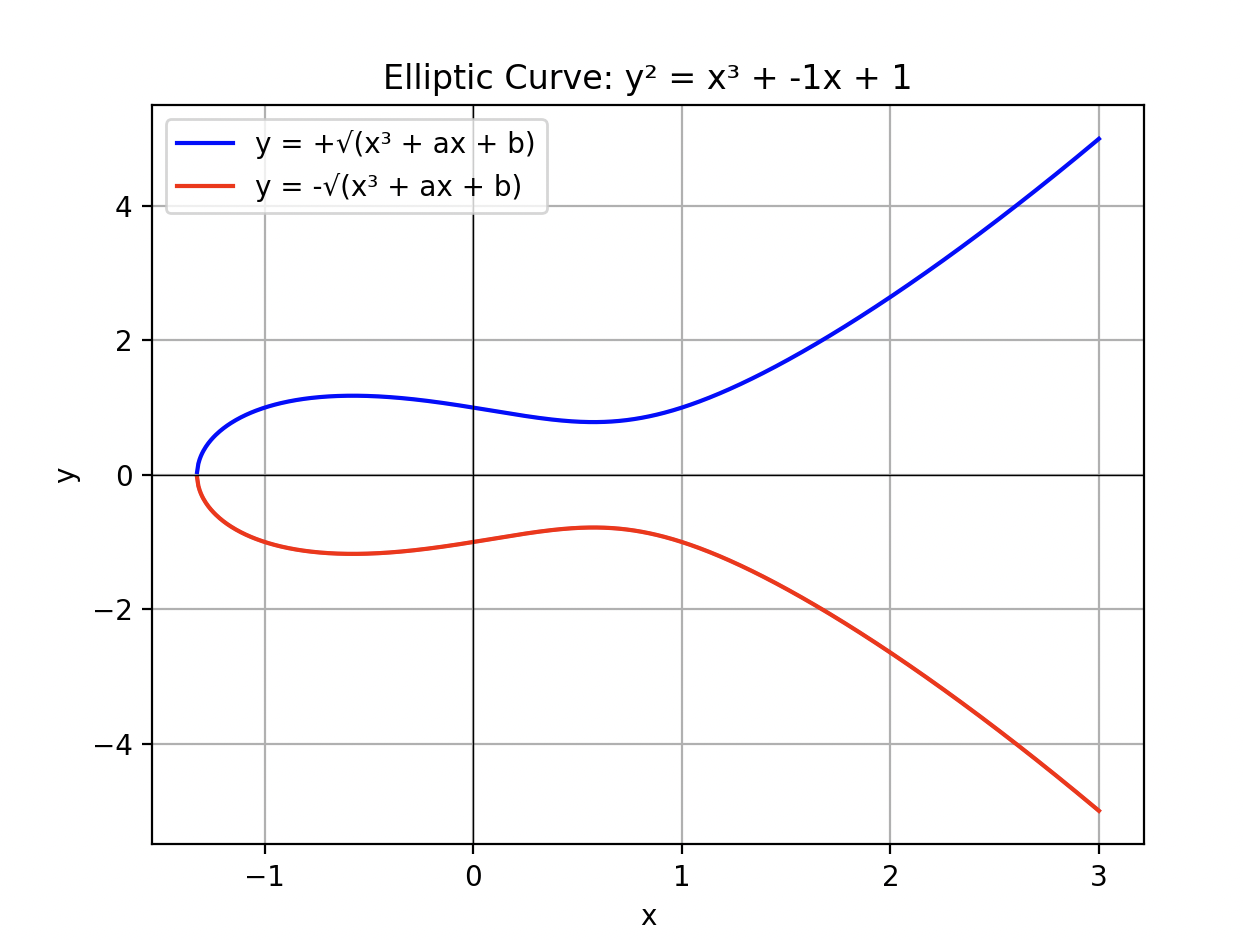
图 1：椭圆曲线在具有常数系数 a=-1 和 b=1 的实数无限域上定义。
椭圆曲线上的点 (x,y) 是 y 和 x 的值，对于给定的 a 和 b，满足上述方程。
曲线必须是非奇异的（即，它没有尖点，也称为尖峰，或自相交）。这可以使用判别式 Δ=4a3+27b2 来检查，它不能为零 (Δ≠0)。这确保了数学运算（如点加法，本文稍后将介绍）在曲线上的每个点处都有明确的定义。
椭圆曲线必须在域 K 上 定义，这意味着坐标 (x,y) 和曲线参数 a 和 b 必须都是域 K 的元素。
当我们提到在某个域 “上” 的椭圆曲线时，我们指定了所有值都来自的集合：
- 实数域上的椭圆曲线 E(R)：坐标和参数是实数，创建平滑、连续的曲线（如图 1 中的曲线）。
- 有限域上的椭圆曲线 E(Fp)：坐标和参数是有限域 𝕡Fp 的元素，创建离散的点集。
我们迄今为止检查的椭圆曲线都是在实数上的，这就是为什么图 1 显示的是连续、平滑的曲线图。这将是本文的重点，但请注意，相同的特征也适用于有限域上的椭圆曲线。
椭圆曲线群
椭圆曲线上的点形成一个集合。当考虑实数时，这当然是满足椭圆曲线方程的无限点集。我们还可以使用称为椭圆曲线点加法的二元运算符将这些点“加”在一起。
将点加在一起的过程比简单地“将 x 坐标相加，然后将 y 坐标相加” 要复杂一些。我们将具体讨论点加法_实际_是如何工作的。但最重要的收获是：
配备有点加法二元运算符的椭圆曲线点集 形成一个阿贝尔群 .
鉴于这个事实，我们可以定义这个 “点加法” 运算符，使其符合阿贝尔群的必要规则。
回想一下，要成为阿贝尔群，点加法运算符下的椭圆曲线点集需要满足以下属性（记住助记符 C learly C yfrin I s I ncredibly A wesome）：
其中，P、Q 和 R 都是椭圆曲线上的点，具有 x 和 y 坐标，+ 是点加法运算符（而不是_常规_加法）。
- 封闭性：集合中两个点之间的点加法产生集合中的另一个点（因此它也将是椭圆曲线上的一个点）。
P+Q=R其中 R 在集合中。
- 单位元：集合中必须存在一个单位元，当使用点加法将其与一个点相加时，结果是该点本身：
P+I=P对于椭圆曲线，单位元是无穷远点 O。为了理解无穷远点，我们将在本文后面介绍不同的坐标系。
- 逆元：集合中的每个点都必须有一个逆元，这样当该点及其逆元与二元运算符结合时，结果是群单位元 O：
P+(-P)=O点 P=(x,y) 的逆元定义为 −P=(x,−y)，并且这些点的加法等于 O。一旦我们定义了点加法，这将更有意义。
- 结合律：
P+(Q+R)=(P+Q)+R- 由于我们说它是一个 阿贝尔 群，因此它也必须是 交换律：
P+Q=Q+P但我们仍然不知道这个神秘的“点加法”运算符是什么，所以让我们定义它。
实数上的椭圆曲线点加法
点加法是椭圆曲线上两个点 P=(x1,y1) 和 Q=(x2,y2) 的加法。它不是“通常”意义上的加法，而是由以下几何规则定义的：
- 如果 P≠Q，则通过两个点 P 和 Q 的线必须与曲线相交于第三个点 R（除非该线是完全垂直的）。这直接来自 Bezout 定理：
Bezouts 定理 指出，两条分别具有 m 和 n 阶的曲线 C 和 D 精确地相交于 mn 个点。
在这里，我们的两条“曲线”是椭圆曲线和连接 P 和 Q 的直线。使用两条线必须相交于三个点的事实，P、Q 和 R：
- 要添加两个点 P+Q ：
-
连接：用一条线连接这些点。
-
相交：找到该线与曲线相交的第三个点 R。
- 反射：关于 x 轴反射
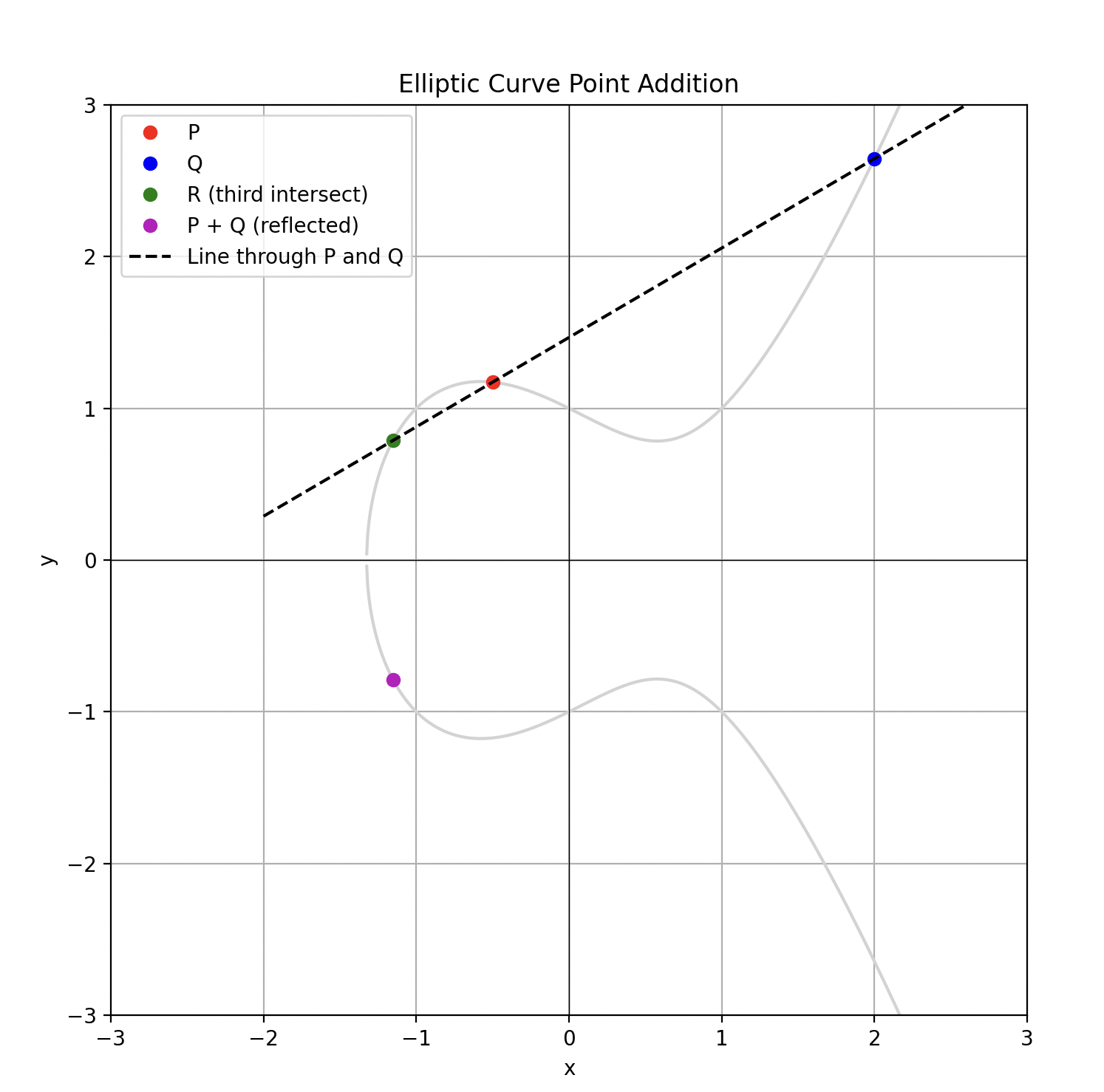
图 2：椭圆曲线点加法。
- 如果一条线与椭圆曲线相交于两个点，那么只要这条线不是完全垂直的，它总是会与曲线相交于第三个点
- 如果 P=Q，则 P 处的切线与曲线相交于曲线上的另一个点 R，并且 2P 定义为此点在 x 轴上的反射。
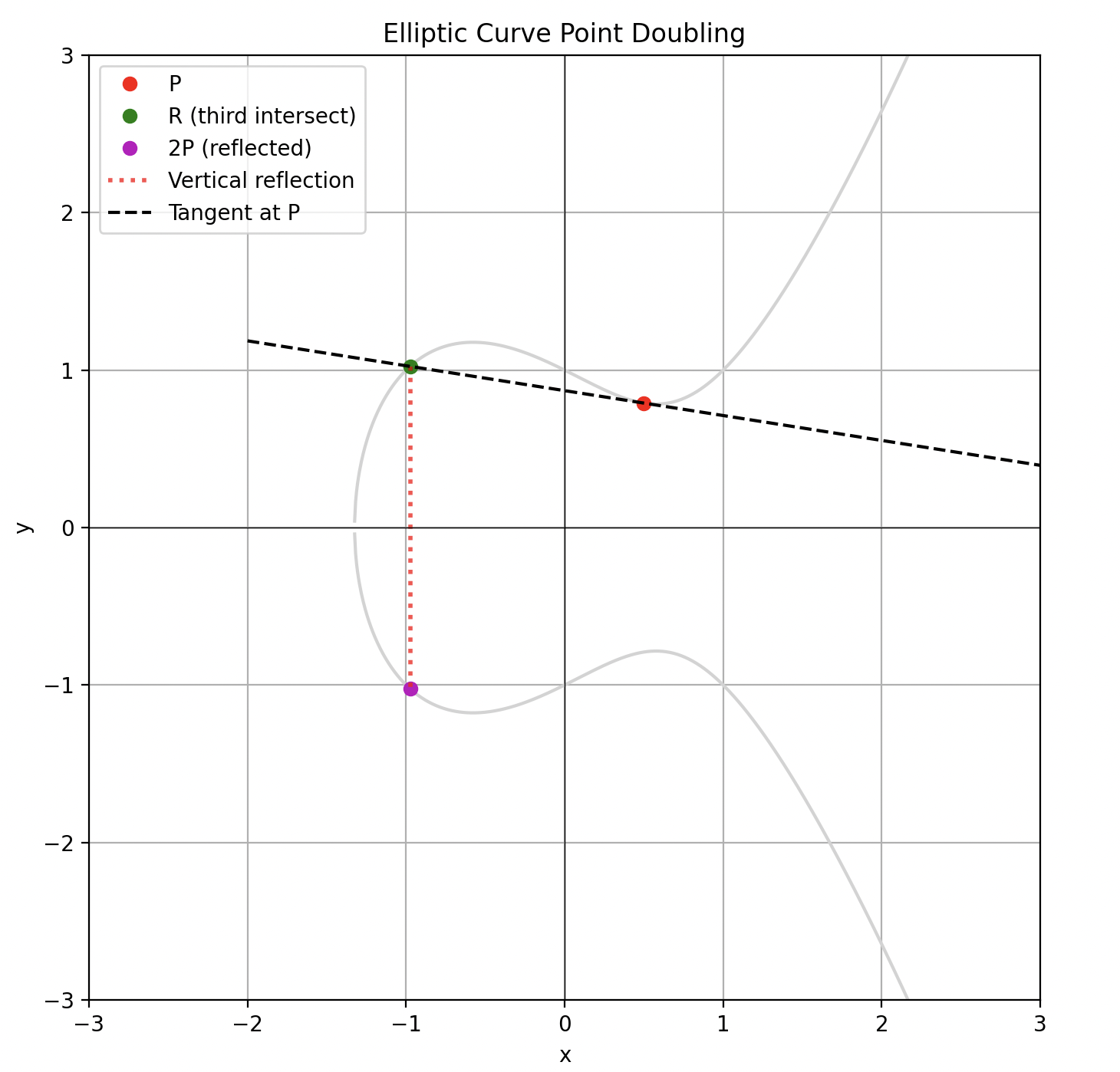
椭圆曲线点倍增。
我们可以使用这个点倍增来定义椭圆曲线点的标量乘法。
点乘法（点之间的乘法）在群中不存在，因为它使用点加法运算符定义。但是，我们可以使用 标量乘法，它定义为一个点与自身相加的次数等于标量。“标量”指的是一个常规数字（如整数），而不是另一个群元素。例如，让我们对 P 进行一些标量乘法：
2P=P+P4P=P+P+P+P或者，更普遍地说：
xP=P+P+...+P // x 次这是标量乘法！请记住，+ 是点加法，它遵循几何规则，而不是_常规_加法。
- 将任何点 P 添加到它的逆元 (−P)：结果始终是群定律定义的 单位元！
P+(-P)=OP 的逆元定义为 −P，其坐标为 (x,−y)。从几何上讲，当 P 和 −P 相加时，连接这两个点的垂直线与椭圆曲线相交于点 O，它是椭圆曲线群的单位元，被称为无穷远点，我们稍后将重新讨论。
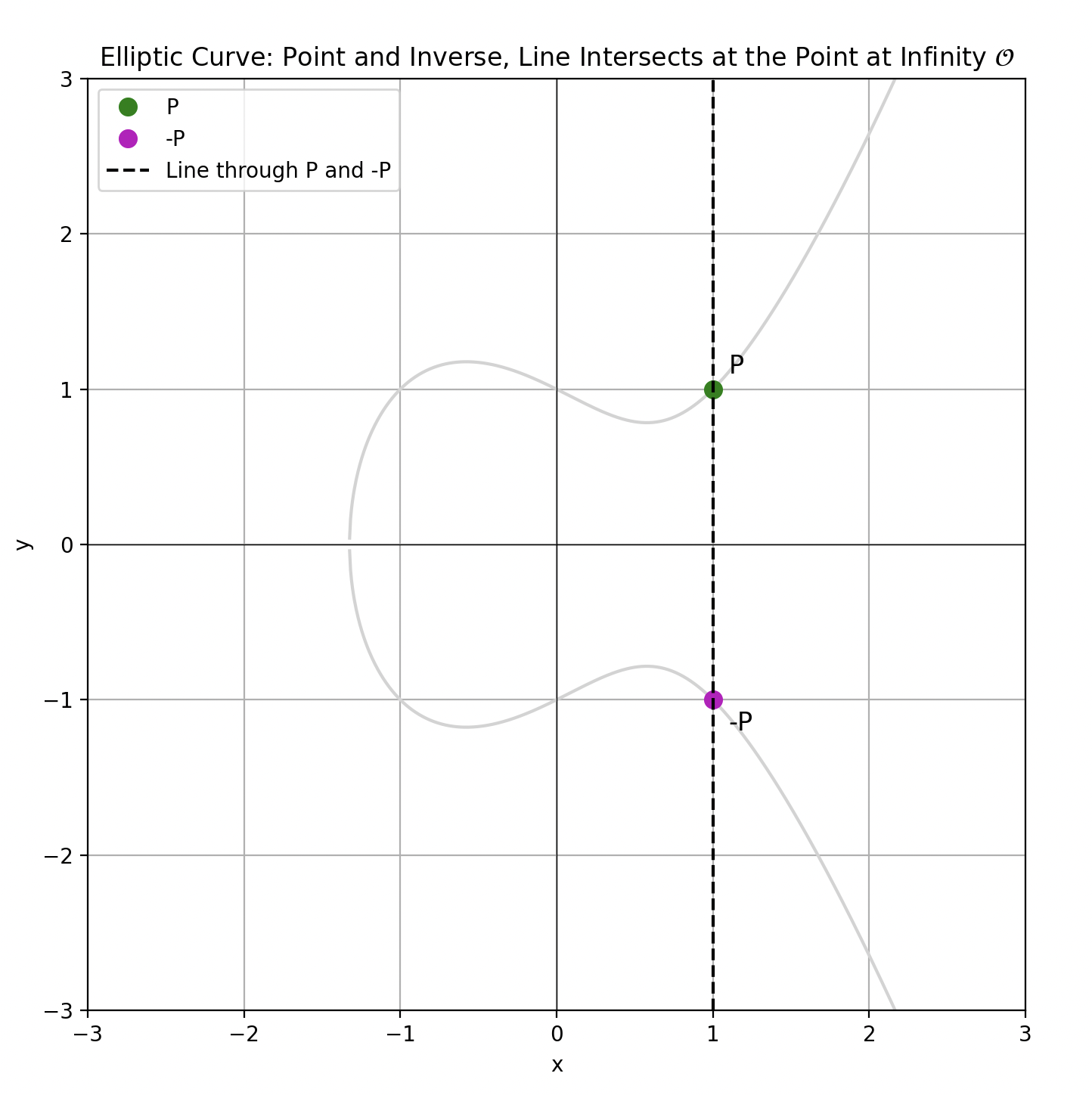
一个点与其逆元的椭圆曲线加法。
为什么我们要将点在 x 轴上反射？
正如我们所说，如果在椭圆曲线上绘制一条通过两个点 P 和 Q 的线，它会与曲线相交于第三个点，我们称之为 R′。
关键的几何事实是：曲线上的三个共线点之和为零：
P+Q+R′=O现在，假设我们将加法定义为 P+Q=R′。那么这个关系将读作：
P+Q+(P+Q)=O简化为
2(P+Q)=O这意味着每个和都是它自己的逆元。这显然违反了群定律：我们将没有一致的单位元或逆元。
为了解决这个问题，我们将和重新定义为第三个点的反射：
P+Q=−R′现在，这个关系变成：
P+Q+(-(P+Q))=O这与每个点都有一个逆元且无穷远点 O 充当单位元的要求一致。
使用这个定义：
- P+(−P)=O（垂直线击中 O），
- 每个点都有一个明确定义的逆元，
- 椭圆曲线点（加上 O）形成一个阿贝尔群。
按照惯例，我们写 P+Q=R，其中 R 已经包含在此反射步骤中。
现在让我们定义 O 是什么。
单位元：无穷远点
无穷远点 O 充当 椭圆曲线的单位元，因此对于所有 P，P+O=P。 这是两条平行线最终相交的点。
直观地说，似乎有道理说 (0,0) 将是单位元，因为任何点加上 (0,0) 都应该返回原始点，对吗？但是，情况并非如此，这可能听起来令人困惑，但原因如下：
- 点加法不是“常规”加法。相反，它涉及遵循上面陈述的几何规则：连接、相交、反射。
- 这些不是“常规”数字，而是椭圆曲线点。
- (0,0) 不在曲线上，因此不在群中。
- 在 射影坐标 中工作时，无穷远点表示为 (0:1:0)，并且确实位于曲线上。这将很快介绍和解释。
在点加法下，无穷远点必须满足以下属性：
- 将 O 添加到任何点 P：结果始终是 P。数学上，P+O=P。这满足了单位元属性。
- 将任何点 P 添加到它的逆元：记住之前的，结果始终是单位元。希望现在我们知道 O 是什么，这应该更有意义：
P+(-P)=O。要真正理解无穷远点，我们需要转移到不同的坐标系：射影坐标。
仿射坐标与射影坐标
仿射坐标 类似于“常规”笛卡尔坐标 (x,y)，但它们在几何变换（如缩放和平移）方面提供了更大的灵活性。
这是因为仿射坐标不需要保留长度和角度等属性，就像笛卡尔坐标一样。这种灵活性允许我们定义椭圆曲线上的点加法等运算，同时保持重要的代数属性（如交换律和结合律）。
不要太纠结于仿射坐标。你需要知道的是，它们是允许我们定义点加法的“常规”坐标。
在仿射坐标中，如上所述，椭圆曲线的 Weierstrass（维尔斯特拉斯） 方程为：
y2=x3+ax+b在这个系统中，无穷远点没有有限的仿射 (x,y) 表示，因此它不位于仿射或 欧几里德平面 中的曲线上。
椭圆曲线通常使用 射影坐标 描述，射影坐标是仿射坐标的扩展，用于处理无穷远点。
关键的见解是，射影坐标不直接对应于空间方向。它们是一种数学形式主义，允许我们表示否则在仿射平面中“无限远”的点。
在射影几何中，点以 齐次坐标 表示，其中 (X:Y:Z)=(2X:2Y:2Z)，如果一个坐标集是另一个坐标的标量倍数，则两个坐标集 (X1:Y1:Z1) 和 (X2:Y2:Z2) 表示同一点。Z 通常被称为缩放因子，表示该点是否位于无穷远处：
- 如果 Z 为 0，则该点位于无穷远处，不同于无穷远点。
- 可以在射影坐标中表示无限多个无穷远点，可以将其视为沿不同方向到达无穷远，例如，(1:2:0)、(3:1:0)、(1:0:0)、(0:1:0) 都是有效的示例。
- 每个都代表不同的“方向”到无穷远
- 虽然射影平面包含整个“无穷远线”（所有 Z=0 的点），但只有此线上的一个点实际满足射影椭圆曲线方程。
- 这个单个无穷远点充当椭圆曲线群的 单位元。
- 无穷远点是 (0:1:0)。这是 Y 方向的无穷远。在仿射平面中可视化曲线时，可以将此点视为连接曲线的两个“分支”，这两个分支在 x 变为无穷大时向上和向下延伸。
仿射坐标 (x,y) 通过变换 x=XZ 和 y=YZ 与射影坐标相关。
检查一下，如果 Z≠0，则恢复原始仿射坐标，如果 Z=0，则该点位于无穷远处！
关键的收获是：
无穷远点 在射影坐标中表示为 (0:1:0)。
使用这些坐标变换，我们可以在 射影坐标 中构造椭圆曲线的 Weierstrass 形式：
(YZ)2=(XZ)3+a(XZ)+b乘以 Z3 给出 射影坐标中椭圆曲线的 Weierstrass 形式：
Y2Z=X3+aXZ2+bZ3最后，代入无穷远点 (0:1:0)，我们可以验证它位于曲线上：
$$Y^2Z = X^3 + aXZ^2+bZ^3 = (1)^2(0) = (0)^3+a(0) _(0)^2+b*(0)^3 = 0$$
因此，无穷远点在射影坐标中得到了很好的定义，位于曲线上，并且是单位元，哇！
就这样，现在我们知道了：
- 什么是椭圆曲线。
- 如何在椭圆曲线点之间进行点加法。
- 如何定义椭圆曲线点群的单位元：无穷远点。
现在，让我们在下一篇文章中看看，当我们定义椭圆曲线时，它如何工作，不是在实数世界中，而是在整数模 p 的有限域中，以及我们如何定义椭圆曲线离散对数问题！
接下来是什么？
虽然实数椭圆曲线可以帮助我们建立几何直觉，但密码学和零知识协议需要在有限域上工作，其中坐标是模某个素数的整数。在下一篇文章中，我们将通过定义 有限域上的椭圆曲线，从连续曲线转移到它们的离散对应物。我们将研究相同的群定律如何适用，以及由于 椭圆曲线离散对数问题 (ECDLP)，这种转变如何在椭圆曲线密码学中实现高效计算和强大的安全保证。
总结
在本文中，我们介绍了：
- 椭圆曲线 由方程 y2=x3+ax+b 定义，在点加法下形成一个阿贝尔群。
- 点加法 遵循“连接-相交-反射”过程，无穷远点 O 充当单位元。
- 标量乘法（重复点加法）构成了椭圆曲线密码学的基础。
- 在点加法期间进行 反射 对于保持组结构中的结合性是必要的。
- 射影坐标 (X:Y:Z) 允许我们正确表示无穷远点 (0:1:0)。
参考文献
- 原文链接： cyfrin.io/blog/zk-math-1...
- 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
