构造与破解SIDH

构建和破解 SIDH

预备知识：椭圆曲线

固定域 $\mathbb{K}$，其中 $\mathrm{char}\,\mathbb{K}\neq 2,3$。$\mathbb{K}$ 的代数闭包记为 $\overline{\mathbb{K}}$，并且是 $\mathbb{K}$ 的一个域扩张，其中每个系数在 $\overline{\mathbb{K}}$ 中的非恒定多项式在 $\overline{\mathbb{K}}$ 中都有一个根。

椭圆曲线可以用短 Weierstrass 方程表示

$E:\quad y^2 = x^3 + a x + b,\qquad a,b\in \mathbb{K}.$

当且仅当判别式

$\Delta \;=\; -16(4a^3+27b^2)$

非零时，这样的曲线是光滑的（非奇异的），这简化为条件 $4a^3+27b^2\neq 0$。 曲线的 $j$-不变量，将在协议中起核心作用，定义为

$j(E) = 1728\frac{4a^3}{4a^3+27b^2}.$

超奇异曲线

假设 $\mathrm{char}\,\mathbb{K}=p>0$。我们称 $E$ 为超奇异的，如果唯一满足 $pP=O$ 的点是 $P=O$，等效地，在 $\overline{\mathbb{K}}$ 上没有非零 $p$-挠点。否则，曲线是普通的。

为什么选择超奇异曲线。

超奇异曲线的一个实际优势是所有超奇异 $j$-不变量都位于 $\mathbb{F}_{p^2}$ 中。因此，我们可以完全在二次域 $\mathbb{F}_{p^2}$ 上执行算术运算，避免在更高次的扩张中进行计算，这会更昂贵。

$\ell$-挠子群

对于 $\ell\ge1$，$\ell$-挠子群由所有被乘以 $\ell$ 湮灭的点组成：

$E[\ell] \;=\; {P\in E(\overline{\mathbb{K}}): \ell P=O}.$

设 $K$ 为一个域，其中 $\operatorname{char}K=p$，E/KE/KE/K 为一个椭圆曲线。用 $E[p]$ 表示 $p$-挠子群。那么

$E[p](\overline K)\ \cong\ {O}\quad\text{or}\quad E[p](\overline K)\ \cong\ \mathbb{Z}/p\mathbb{Z}.$

等效地，

$E \text{ is supersingular } \Longleftrightarrow E[p](\overline K)={O},$

而对于普通曲线，有 $E[p](\overline K)\cong \mathbb{Z}/p\mathbb{Z}$。

示例

让我们找出在 $\mathbb{F}_5$ 上定义的曲线 $y^2=x^3+x+3$ 的 2-挠子群。2-挠子群的定义是

$E[2] \;=\; {P\in E(\overline{\mathbb{F}_5}): 2P=O}.$

如果我们将其可视化，则 2-挠点是 x 轴上的交点

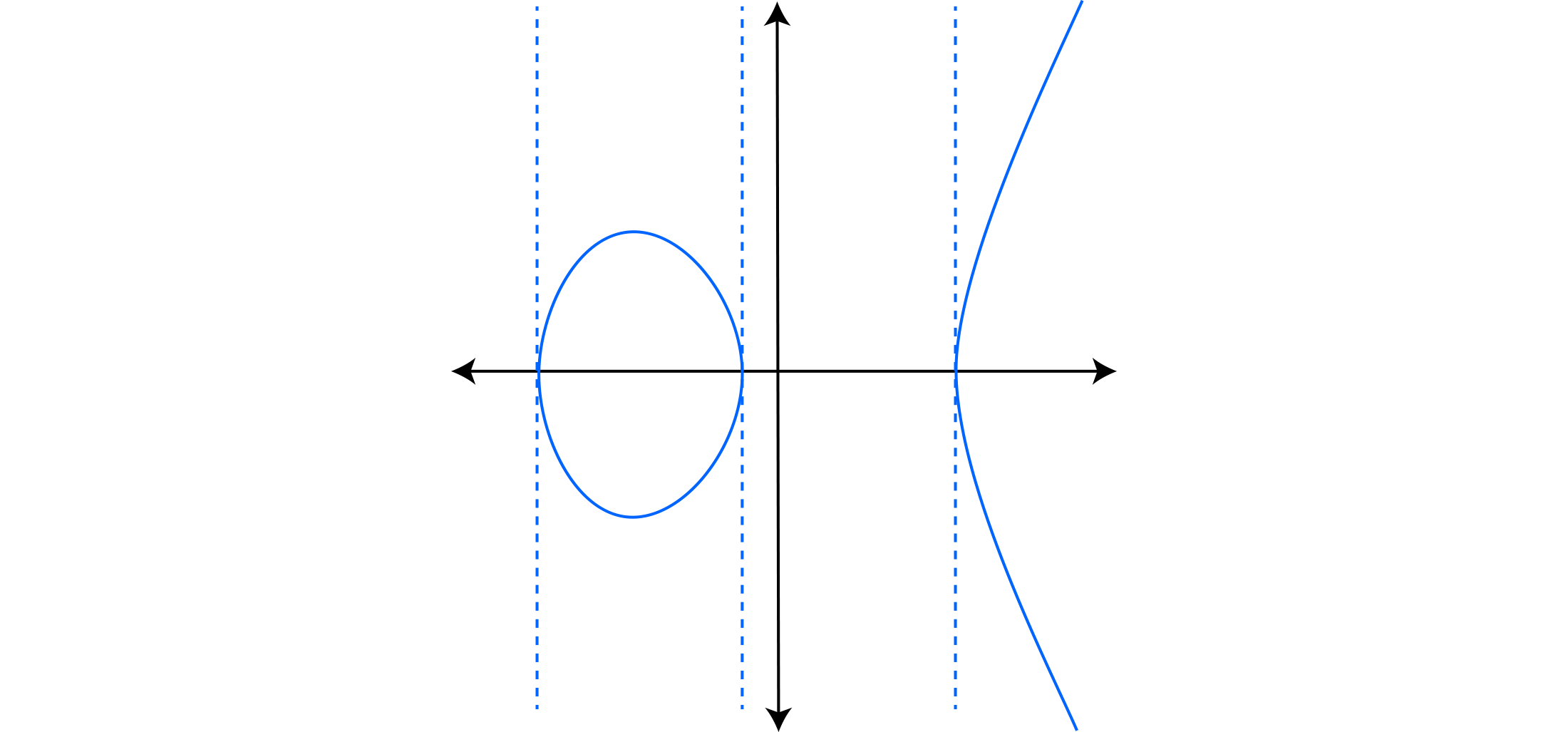
因此，要找到这些点，我们需要求解 $x^3 + x + 3 = 0$

### 域和曲线
F = GF(5)
E = EllipticCurve(F, [0, 0, 0, 1, 3])     # y^2 = x^3 + 1*x + 3

### --- 2-挠准则（char ≠ 2）：具有 y=0 和 x 是 f(x)=x^3 + x + 3 的根的点
R.<x> = PolynomialRing(F)
f = x^3 + x + 3
print("Over F_5, f factors as:", f.factor())

###  我们只看到一个线性因子 (x-1)，所以只有 (1,0) 是 F_5 上的 2-挠
P_F5 = E(1,0)
print("Check 2*P_F5 == O?", 2*P_F5 == E(0))

### --- 转到二次扩张以获得完整的 E[2]
K.<u> = GF(5^2)                         ## 二次扩张
EK = E.change_ring(K)
R2.<x> = PolynomialRing(K)
fK = R2(f)
print("Over F_25, f factors as:", fK.factor())

### 收集 F_25 上的所有 2-挠点：三个根给出 (x_i, 0)，加上 O
roots = [r for (r, mult) in fK.roots()]  ## K 中的三个不同的根（因为 char!=2 和 Δ ≠ 0）
E2 = [EK(0)] + [EK(r, K(0)) for r in roots]
print("E[2] over F_25 has size:", len(E2))
print("E[2] points:")
for Q in E2:
    print(" ", Q)

### 理智检查：每个非零 2-挠点的阶数为 2
print("Orders of nonzero 2-torsion points:")
for Q in E2[1:]:
    print(Q.order())

运行代码后，我们看到子群中有 3 个非平凡的 2-挠点以及无穷远点。

同源

同源 $\varphi:E_1\to E_2$ 是由有理函数给出的非恒定群同态。这样的映射自动是满射的，具有有限的核。在短 Weierstrass 模型上，在归一化使得 $\varphi(O)=O$ 之后，同源采用仿射形式

$\varphi(x,y)=\Big(\frac{f_1(x)}{g_1(x)},\; y\cdot\frac{f_2(x)}{g_2(x)}\Big),$

其中度定义为 $\deg\varphi=\max{\deg f_1,\deg g_1}$。当 $\varphi$ 是可分的时，意味着导数 $(\tfrac{f_1}{g_1})'$ 不完全为零，则度等于核的大小：$\deg\varphi=#\ker\varphi$。

超奇异性由同源性保持：

$E_1 \text{ supersingular } \Longleftrightarrow E_2 \text{ supersingular.}$

示例

让我们看一下从在 $\mathbb{F}_5$ 上定义的椭圆曲线 $y^2=x^3+x+3$ 到自身的同源，该同源由乘以 2 的映射定义。同源将每个点 $P$ 映射到它的两倍

$\varphi: P \to 2P$

### 域和曲线
F = GF(5)
E = EllipticCurve(F, [0, 0, 0, 1, 3])     ## y^2 = x^3 + 1*x + 3
### --- 转到二次扩张
K.<u> = GF(5^2)                         ## 二次扩张
EK = E.change_ring(K)

Xmap, Ymap = EK.multiplication_by_m(2)
print("x(2P) =", Xmap)
print("y(2P) =", Ymap)

因此，加倍一个点的映射是

$(x,y) \to \big( \dfrac{x^4 - 2x^2 + x + 1}{-x^3 - x + 2}, \dfrac{-2x^6y - xy + y}{-x^6 - 2x^4 - x^3 - x^2 - x + 1} \big)$

此同源的核恰好是我们之前看到的 2-挠子群，其基数为 4，这与我们的同源的度一致。

组合和对偶性

如果 $\varphi:E\to E'$ 且 $\psi:E'\to E''$ 是同源，则它们的组合

$\psi\circ\varphi:\ E \longrightarrow E''$

再次是一个同源，并且它的度相乘：

$\deg(\psi\circ\varphi)=\deg\psi\cdot\deg\varphi.$

同构只是一个度为 $1$ 的同源，其核为 ${O}$；将同构与其逆组合是单位元。对于一个一般的度为 $d>1$ 的同源 $\varphi:E\to E'$，在通常意义上没有逆。相反，存在一个唯一的对偶同源 $\widehat{\varphi}:E'\to E$，它“类似于”乘以 $d$ 的逆：

$\widehat{\varphi}\circ \varphi=[d]\ \text{ on }E,\qquad \varphi\circ \widehat{\varphi}=[d]\ \text{ on }E'.$

因此，组合返回到同一条曲线，并且其核是完整的 $d$-挠：

$\ker(\widehat{\varphi}\circ\varphi)=E[d],\qquad \ker(\varphi\circ\widehat{\varphi})=E'[d].$

同构和 $j$-不变量

在 $\mathbb{K}$ 上的同构 $\psi: E_1 \to E_2$ 是度为 1 的同源，采用以下形式

$(x,y)\longmapsto (u^2x,\;u^3y),\qquad u\in\mathbb{K}^\times.$

同构保留 $j$-不变量：如果 $\psi:E_1\to E_2$ 是一个同构，则 $j(E_1)=j(E_2)$。在代数闭域上，逆命题成立：两条椭圆曲线同构当且仅当它们的 $j$-不变量重合。

特征 $p$ 中的超奇异 $j$-不变量的数量为

$s_p \;=\; \Big\lfloor \frac{p}{12}\Big\rfloor + \varepsilon_p, \quad \varepsilon_p\in{0,1,2}, \quad s_2=s_3=1,$

给出大约 $s_p\approx p/12$ 个这样的不变量。

从核构造同源

在某些应用中，我们知道所需同源的核，但需要构造显式映射。具体来说，给定一个椭圆曲线 $E$ 和一个有限子群 $G \subseteq E$，我们希望计算同源 $\varphi: E \to E/G$，其核恰好是 $G$。

Vélu 的公式解决了这个问题。它们以定义曲线 $E: y^2 = x^3 + ax + b$ 的系数 $(a, b)$ 和子群 $G$ 中所有非零点的列表（或者当 $G$ 是循环群时，仅需一个生成元）作为输入。根据这些数据，Vélu 的公式产生：

1. 定义同源的有理函数 $\varphi(x,y) = (X(x), Y(x,y))$，和
2. 陪域曲线 $E/G: y^2 = x^3 + a'x + b'$ 的系数 $(a', b')$。

对于阶数为 $m$ 的循环子群 $\langle P\rangle$，得到的同源

$\varphi:\ E \longrightarrow E/\langle P\rangle$

是可分的，并且 $\deg\varphi = m = #\ker\varphi$。这种核优先方法是基于同源密码学的根本，在这种密码学中，各方通过选择秘密核生成元来构建秘密同源。

### F_5 上的基曲线，然后扩展到 F_{5^2}，以便完全定义 E[2]
F = GF(5)
E = EllipticCurve(F, [0,0,0,1,3])           ## y^2 = x^3 + x + 3
K.<u> = GF(5^2)
EK = E.change_ring(K)

### E[2] 点：x^3 + x + 3 的根，其中 y=0
R.<x> = PolynomialRing(K)
f = x^3 + x + 3
roots = [r for (r, _) in f.roots()]         ## K 中的 3 个不同的根
E2_pts = [EK(r, K(0)) for r in roots]       ## 三个非零 2-挠点

### 传递核子群的生成器列表（任何两个独立的 E[2] 点）
phi2 = EllipticCurveIsogeny(EK, E2_pts[:2])               ## 使用 Vélu，其核由这些点生成
E2cod = phi2.codomain()
print("deg(phi2) =", phi2.degree())         ## 应该是 4

### 核的完整性检查：E[2] 的所有点（包括 O）都映射到 O
for Q in [EK(0)] + E2_pts:
    assert phi2(Q) == E2cod(0)
print("Kernel OK (E[2] → O).")

在 SageMath 中，EllipticCurveIsogeny 构造函数将起始曲线和一个或多个生成核的点作为输入，并使用 Vélu 的公式来构造同源。

SIDH 协议

协议参数

SIDH 以以下形式的素数开始

$p = 2^{e_A}3^{e_B} - 1,$

其中 $e_A$ 和 $e_B$ 是正整数，选择它们使得 $2^{e_A} \approx 3^{eB}$。所有计算都在二次扩张域 $\mathbb{F}{p^2}$ 上执行。

这个素数结构是经过精心选择的。对于在 $\mathbb{F}{p^2}$ 上定义的超奇异曲线 $E$，$\mathbb{F}{p^2}$-有理点的数量为

$#E(\mathbb{F}_{p^2}) = (p+1)^2,$

并且群结构为

$E(\mathbb{F}{p^2}) \cong \mathbb{Z}{p+1} \times \mathbb{Z}_{p+1}.$

由于 $p+1 = 2^{e_A}3^{e_B}$，因此曲线包含每个除以 $2^{e_A}3^{e_B}$ 的阶数的点。这使 Alice 和 Bob 能够使用 2 和 3 的幂独立地遍历它们各自的同源图。

同源图

该协议在两个共享相同顶点集但具有不同边结构的超奇异同源图上运行。

顶点表示 $\mathbb{F}_{p^2}$ 上超奇异椭圆曲线的同构类，可以通过其 $j$-不变量唯一地识别。

边由同源定义：对于与 $p$ 互质的素数 $\ell$，如果存在 $\mathbb{F}_{p^2}$ 上的可分 $\ell$-同源 $\varphi: E \to E'$，则 $\ell$-边连接顶点 $[E]$ 和 $[E']$。

对于 $\ell \neq p$，$\ell$-挠子群具有结构

$E[\ell] \cong (\mathbb{Z}/\ell\mathbb{Z})^2,$

包含恰好 $\ell + 1$ 个阶数为 $\ell$ 的循环子群。每个循环子群 $G \subseteq E[\ell]$ 通过 Vélu 的公式确定一个唯一的可分同源 $\varphi_G: E \to E/G$。因此，$\ell$-同源图中的每个顶点都恰好有 $\ell + 1$ 个邻居。

对于 Alice 的 2-同源图，每个顶点都有 3 个向外的边（几乎没有例外）。对于 Bob 的 3-同源图，每个顶点都有 4 个向外的边。

公共参数

该协议需要一个固定的、在 $\mathbb{F}_{p^2}$ 上定义的超奇异起始曲线 $E_0$ 和两对挠基点：

${P_A, Q_A} \subset E_0[2^{e_A}], \qquad {P_B, Q_B} \subset E_0[3^{e_B}].$

这些基生成挠子群

$E_0[2^{e_A}] \cong (\mathbb{Z}/2^{e_A}\mathbb{Z})^2, \qquad E_0[3^{e_B}] \cong (\mathbb{Z}/3^{e_B}\mathbb{Z})^2.$

密钥生成

Alice 的密钥生成：

Alice 选择一个秘密整数 $k_A \in {0, 1, \ldots, 2^{e_A} - 1}$ 并构造核生成元

$R_A = P_A + [k_A]Q_A.$

循环子群 $G_A = \langle R_A \rangle \subset E_0[2^{e_A}]$ 的阶数为 $2^{e_A}$。Alice 计算同源

$\varphi_A: E_0 \to E_A := E_0/G_A$

作为 $e_A$ 个连续的 2 次同源的组合，有效地遍历了 2-同源图中的 $e_A$ 条边。

Alice 的公钥是

$\text{PK}_A = (E_A, \varphi_A(P_B), \varphi_A(Q_B)).$

公钥包括图像曲线 $E_A$ 和 Bob 的挠基点在她的秘密同源下的图像。

Bob 的密钥生成：

Bob 遵循使用 3 次幂同源的类似过程。他选择一个秘密 $k_B \in {0, 1, \ldots, 3^{e_B} - 1}$ 并构造RB=PB+[kB]QB,GB=⟨RB⟩⊂E0[3eB].$R_B = P_B + [k_B]Q_B, \qquad G_B = \langle R_B \rangle \subset E_0[3^{e_B}]$.

Bob 计算同源

φB:E0→EB:=E0/GB$\varphi_B: E_0 \to E_B := E_0/G_B$

作为 $e_B$ 个连续的 3 次同源的组合。

Bob 的公钥是

PKB=(EB,φB(PA),φB(QA)).$\text{PK}_B = (E_B, \varphi_B(P_A), \varphi_B(Q_A))$.

共享密钥计算

Alice 的计算：

收到 Bob 的公钥后，Alice 构造

$S'_A = \varphi_B(P_A) + [k_A]\varphi_B(Q_A) = \varphi_B(P_A + [k_A]Q_A) = \varphi_B(R_A)$,

利用同源是群同态的事实。循环子群 ⟨SA′⟩$\langle S'_A \rangle$ 等于 φB(GA)$\varphi_B(G_A)$，即 Alice 的原始核在 Bob 的同源下的图像。

然后 Alice 计算

ϕA′:EB→EBA:=EB/⟨SA′⟩.$\phi'_A: EB \to E{BA} := E_B / \langle S'_A \rangle$.

Bob 的计算：

Bob 执行对称计算，构造

$S'_B = \varphi_A(P_B) + [k_B]\varphi_A(Q_B) = \varphi_A(R_B)$

因此 ⟨SB′⟩=φA(GB)$\langle S'_B \rangle = \varphi_A(G_B)$，并计算

$\phi'_B: EA \to E{AB} := E_A / \langle S'_B \rangle$.

共享密钥：

同源理论的一个基本定理保证了一个规范同构

(E0/GA)/φA(GB)≅(E0/GB)/φB(GA),(E_0/G_A)/\varphi_A(G_B) \cong (E_0/G_B)/\varphi_B(G_A),

这意味着 EAB≅EBA$E{AB} \cong E{BA}$ 并且因此 j(EAB)=j(EBA)$j(E{AB}) = j(E{BA})$。

共享密钥是通用的 jjj-不变量：

Shared secret=j(EAB)=j(EBA)$\boxed{\text{Shared secret} = j(E{AB}) = j(E{BA})}$

双方都得到同构的曲线并计算相同的 jjj-不变量。SIDH 的安全性依赖于从 E0$E_0$ 和 EA$E_A$（或 EB$E_B$）的知识中确定同源 φA$\varphi_A$ (或 φB$\varphi_B$) 的计算难度，这个问题被认为即使对于量子计算机也很难。

示例演示

对于我们的例子，我们选择素数为 p=2433−1$p = 2^4 3^3 -1$，起始曲线 E0 为 y2=x3+a0x2+xE_0 \text{ is } y^2=x^3 + a_0x^2 + x，其中 a0=329i+423$a_0 = 329i+ 423$。接下来，我们为 Alice 和 Bob 确定基点

$$ \begin{aligned} P_A := (100i + 248, 304i + 199) \quad Q_A := (426i + 394, 51i + 79) \ P_B := (358i + 275, 410i + 104) \quad Q_B := (20i + 185, 281i + 239) \end{aligned} $$

Alice 生成一个秘密数字 kA=11$k_A = 11$ 并计算核生成器点

$S_A = P_A + [k_A]Q_A = (271i + 79, 153i + 430)$.

该点的阶数为 16，可以表示一个 16 度的同源，或者 4 个 2 度同源的组合。后一种方法有利于计算，因此 Alice 使用 Vélu 公式计算同源图中的 4 个“跳”，并在图像曲线上着陆，这将是她的公钥（由其 Montgomery 参数编码），以及 Bob 在同一秘密同源下的基点。

$$ PK_A = (\varphi_A(E_0), \varphi_A(P_B), \varphi_A(Q_B)) \ = (423i + 179,(142i + 183, 119i + 360),(220i + 314, 289i + 10)) $$

下图显示了 Alice 在其各自曲线的 jjj-不变量上进行的“跳跃”。

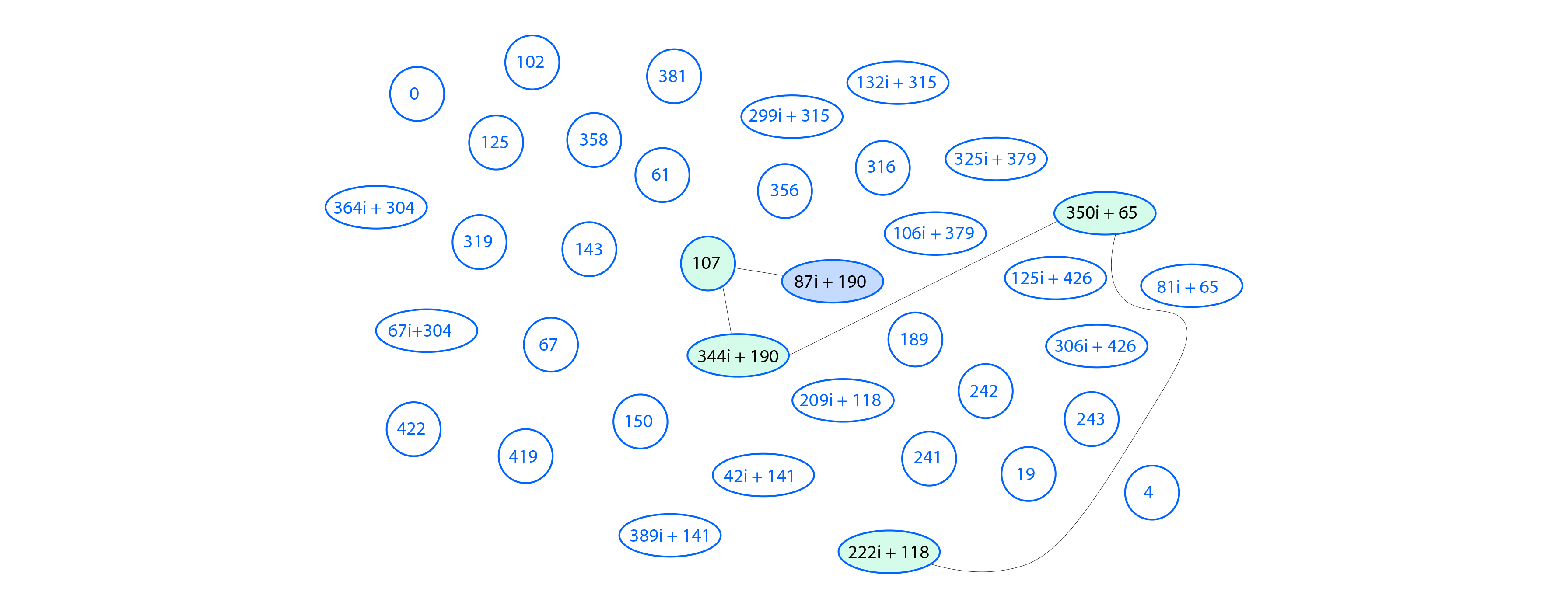
Bob 也选择一个秘密参数 kB=2$k_B = 2$ 并计算相应的生成器点

SB=PB+[kB]QB=(122i+309,291i+374).$S_B = P_B + [k_B]Q_B = (122i + 309, 291i + 374)$.

其阶数为 27，意味着 Bob 可以将其解释为 3 个 3 度同源的组合。他的公钥也是生成的曲线以及 Alice 在他的秘密同源下的基点

PKB=(φB(E0),φB(PA),φB(QA))=(273i+76,(187i+226,43i+360),(325i+415,322i+254))PK_B = (\varphi_B(E_0), \varphi_B(P_A), \varphi_B(Q_A)) \ = (273i + 76,(187i + 226, 43i + 360),(325i + 415, 322i + 254))

现在进行共享密钥计算，Alice 从 Bob 公钥中获取 Bob 的 codomain 曲线作为起点，然后使用 Bob 提供的她的基点的图像来计算内核

$S'_A = \varphi_B(P_A) + [k_A]\varphi_B(Q_A) = (125i + 357, 415i + 249)$.

就像之前一样，使用 SA′$S'_A$ 生成的内核计算图像曲线。

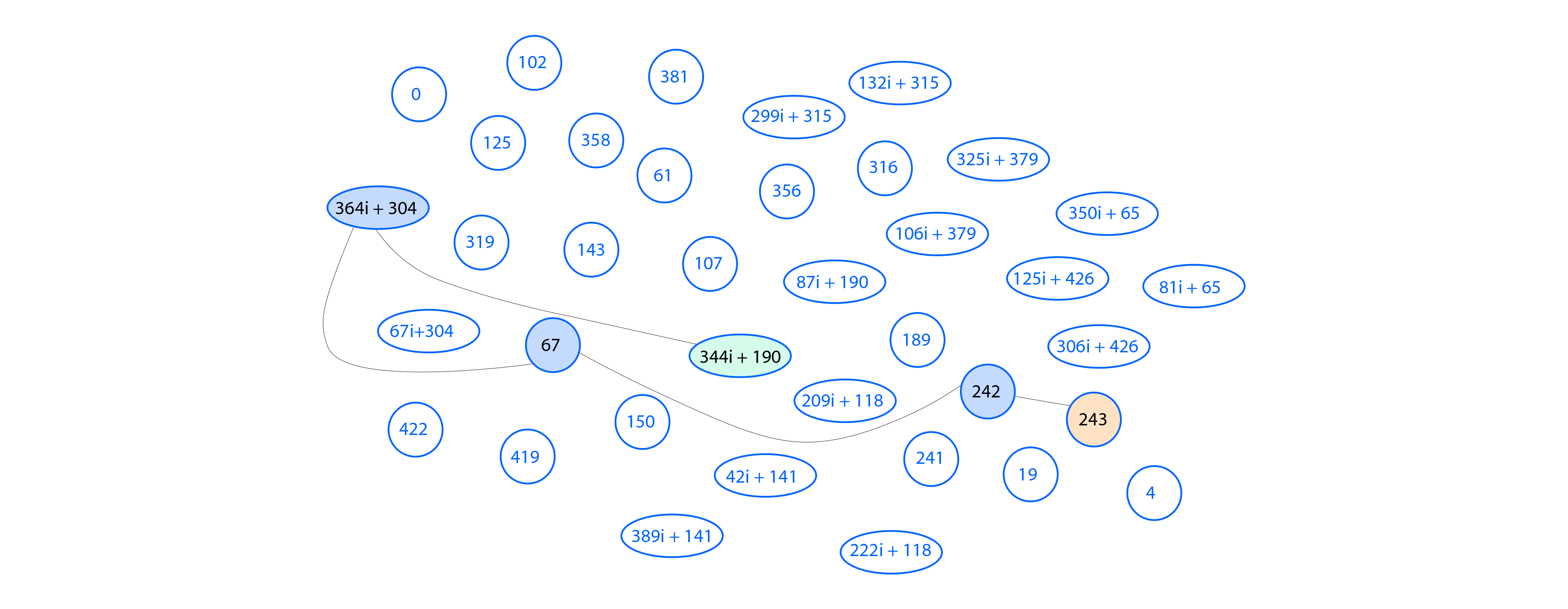
Bob 经过相同的步骤，最终得到

$S'_B = \varphi_A(P_B) + [k_B]\varphi_A(Q_B) =(393i + 124, 187i + 380)$.

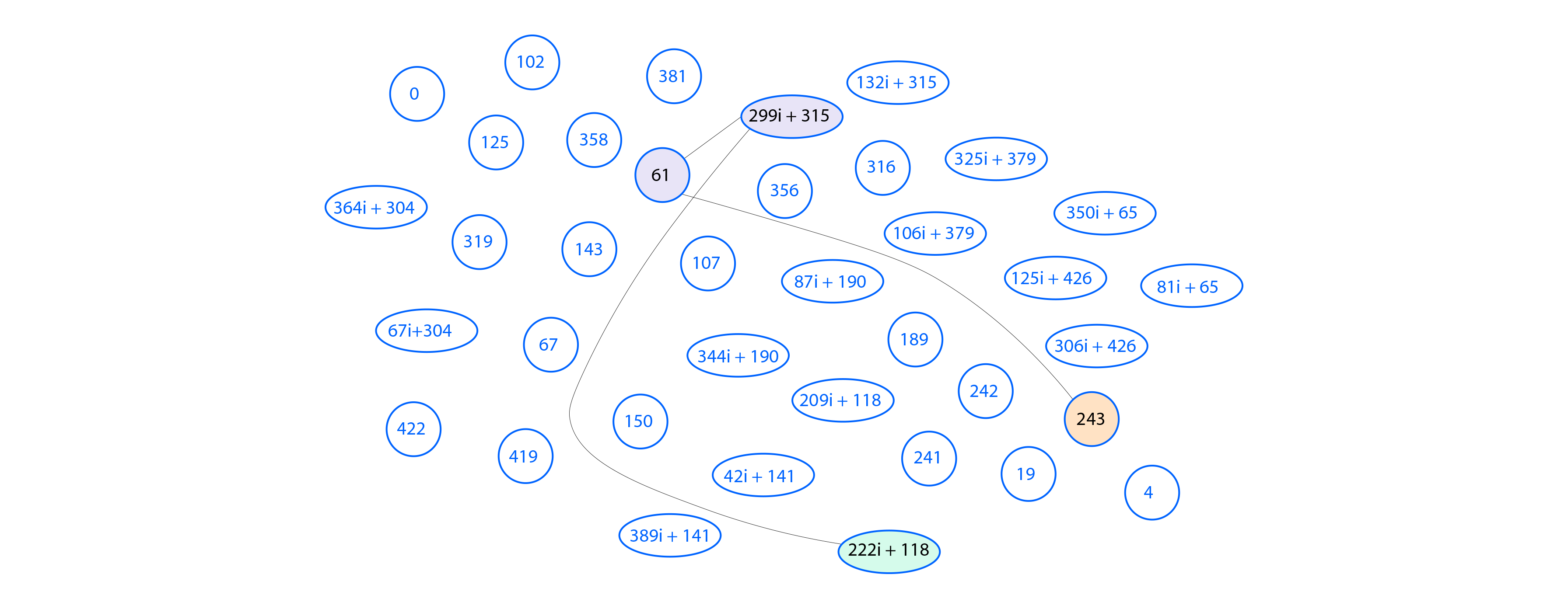
经过这些步骤后，他们都到达 jjj-不变量 = 243 的节点，并且该共享密钥可用于派生加密密钥。

Castryck-Decru 攻击

安全问题和攻击策略

SIDH 的安全性取决于以下问题的困难性：给定两个超奇异曲线 E0$E_0$ 和 EB=E0/⟨RB⟩$E_B=E_0/\langle R_B\rangle$，恢复定义 3eB$3^{e_B}$ 度可分离同源的秘密循环核 ⟨RB⟩$\langle R_B\rangle$。

当沿着 3-同源路径行走时，第一步有 4 个 3 度选择。在排除对偶边（返回到先前的曲线）之后，每个后续步骤仍然有 3 个选择。如果存在一个 oracle 可以测试提议的下一个 3-同源是否位于秘密路径上，则可以通过测试每个级别的 3 个候选者来恢复整个路径。

Castryck-Decru 攻击通过从椭圆曲线（维度 1）提升到主要极化阿贝尔曲面（维度 2）来构建这样的 oracle，其中测试曲面是 Jacobian 还是椭圆曲线的乘积提供了所需的信号。

Oracle 构建

核心思想基于 Kani 的一个定理，该定理将同源菱形图与椭圆曲线的乘积相关联。

该攻击通过以下方式在维度 2 中构建这样的菱形图：

1. 从椭圆曲线 C×Eicand$C \times E_i^{\text{cand}}$ 的乘积开始
2. 使用一个 (2eA,2eA)$(2^{e_A}, 2^{e_A})$-同源，将该乘积“粘合”成一个 genus-2 Jacobian
3. 计算 Richelot (2,2)$(2,2)$-同源链（椭圆曲线之间 2 度同源的高维模拟）
4. 测试最终的 codomain 是否分裂回一个乘积

关键的见解是，当且仅当候选 3-同源 Ei−1→Eicand$E_{i-1} \to E_i^{\text{cand}}$ 位于 Bob 的秘密路径上时，最终曲面才是椭圆曲线的乘积。这遵循 Kani 的定理以及菱形图的特定结构。

由于维度 2 的随机主要极化阿贝尔曲面是 Jacobian 的概率约为 1−1/p$1 - 1/p$，而乘积发生的概率约为 1/p$1/p$，因此该测试可以可靠地区分正确和不正确的候选者。

攻击算法

该攻击通过一次确定一步来恢复 Bob 的 3eB$3^{e_B}$ 度秘密同源 φB:E0→EB=E0/⟨RB⟩$\varphi_B: E_0 \to E_B = E_0/\langle R_B\rangle$。由于 Bob 将他的同源计算为 eB$e_B$ 个连续 3 度同源的组合，因此攻击者使用维度 2 oracle 恢复链中的每个单独的 3-同源。

输入

• 起始曲线 E0$E_0$
• 图像曲线 EB=E0/⟨RB⟩$E_B = E_0/\langle R_B\rangle$
• 来自 Bob 公钥的挠率图像 (φB(PA),φB(QA))$(\varphi_B(P_A), \varphi_B(Q_A))$，其中 {PA,QA}\{P_A, Q_A\} 生成 E0[2eA]$E_0[2^{e_A}]$

迭代恢复过程

Bob 的秘密同源是 eB$e_B$ 个 3 度同源的组合：

$\varphiB = \varphi{eB} \circ \varphi{e_B-1} \circ \cdots \circ \varphi_2 \circ \varphi_1: E_0 \to E_1 \to E2 \to \cdots \to E{e_B} = E_B$

该攻击按顺序恢复这些同源。在步骤 iii 中，已经恢复了 φ1,…,φi−1$\varphi1, \ldots, \varphi{i-1}$，攻击者知道当前曲线 Ei−1$E_{i-1}$ 并试图确定 φi:Ei−1→Ei$\varphii: E{i-1} \to E_i$。

步骤 iii：恢复下一个 3-同源

1. 识别候选边：

从曲线 Ei−1$E{i-1}$ 开始，有 4 个传出的 3-同源。但是，其中之一是传入同源 φi−1$\varphi{i-1}$ 的对偶，可以排除（第一步除外）。这留下了 3 个候选边进行测试。

2. 构建辅助同源：

oracle 需要一个 c=2eA−3eB−i$c = 2^{e_A} - 3^{e_B - i}$ 度的辅助同源。假设 E0$E_0$ 具有已知的自同态（例如满足 2i∘2i=[−4]$2i \circ 2i = [-4]$ 的 2i$2i$），并且假设 ccc 可以写成 c=u2+4v2$c = u^2 + 4v^2$，构造 ccc 度自同态：

$\gamma: E_0 \to C, \quad \gamma = [u] + [v] \circ 2i$. 在生成器上评估 γ$\gamma$ 以获得：

$P_c = \gamma(P_A), \qquad Q_c = \gamma(Q_A) \in C[2^{e_A}]$.

3. 测试每个候选者：

对于 3 个候选同源中的每一个 φicand:Ei−1→Eicand$\varphii^{\text{cand}}: E{i-1} \to E_i^{\text{cand}}$:

a. 通过候选路径推送挠率：

计算生成器在已恢复路径和候选者的组合下的图像：

$P_i^{\text{cand}} = \varphi_i^{\text{cand}} \circ \cdots \circ \varphi_1(P_A), \qquad Q_i^{\text{cand}} = \varphi_i^{\text{cand}} \circ \cdots \circ \varphi_1(Q_A)$. b. 形成菱形核：

考虑 $C \times E_i^{\text{cand}}$ 的 $(2^{e_A}, 2^{e_A})$ 子群，该子群由以下各项生成： $\langle (P_c, P_i^{\text{cand}}), (Q_c, Q_i^{\text{cand}}) \rangle$. 该子群始终定义一个 $(2^{e_A}, 2^{e_A})$-同源。

c. 粘合到维度 2：

该 $(2^{e_A}, 2^{e_A})$-同源的第一步是一个粘合映射，该映射将椭圆曲线 C×Eicand$C \times E_i^{\text{cand}}$ 的乘积映射到 genus-2 曲线 Jac(H)$\text{Jac}(H)$ 的 Jacobian。

d. 计算 Richelot 链：

组成 $e_A - 1$ 个连续的 Richelot )$(2,2)$-同源： $\text{Jac}(H_0) \to \text{Jac}(H1) \to \cdots \to \text{Jac}(H{eA-1}) \to A{e_A}$. e. 测试分裂：

在 Richelot 同源链之后，检查最终 $(2,2)$-同源是否分裂——也就是说，其 codomain AeA$A_{e_A}$ 是两个椭圆曲线的乘积，而不是 genus-2 曲线的 Jacobian。

该测试很简单：在 Richelot 公式中，出现了一个特定的行列式 δ$\delta$。当且仅当 δ=0$\delta = 0$ 时，codomain 才是乘积。

f. 应用 Kani 定理：

• 如果 δ=0$\delta = 0$（分裂）： 根据 Kani 定理，当且仅当候选 φicand$\varphi_i^{\text{cand}}$ 位于真正的秘密路径上时，才会发生这种情况。攻击者找到了正确的下一个边。
• 如果 δ≠0$\delta \neq 0$（Jacobian）：候选者不正确。由于随机阿贝尔曲面是乘积的概率约为 1/p$1/p$，因此该测试可以可靠地区分正确和不正确的候选者。
  4. 进入下一步：

一旦确定了使菱形图分裂的唯一候选者，请设置 φi=φicand$\varphi_i = \varphi_i^{\text{cand}}$ 并将当前曲线更新为 Ei$E_i$。继续执行步骤 i+1$i+1$。

终止和输出

经过 $e_B$ 次迭代后，已恢复完整的链 φ1∘φ2∘⋯∘φeB$\varphi_1 \circ \varphi2 \circ \cdots \circ \varphi{e_B}$。这确定了 Bob 的秘密同源 φB$\varphi_B$ 及其核 ⟨RB⟩$\langle R_B \rangle$。

就 Bob 的密钥而言：如果 Bob 的私钥是整数 kB∈[0,3eB)$k_B \in [0, 3^{e_B})$ 使得 ker⁡φB=⟨PB+[kB]QB⟩$\ker \varphi_B = \langle P_B + [k_B]Q_B \rangle$，则该攻击一次恢复一个 base-3 数字 kB$k_B$。

为什么辅助信息会启用攻击

该攻击的一个关键方面是它依赖于 SIDH 公钥中的挠率点信息。回想一下，Alice 的公钥不仅包括她的图像曲线 $ E_A$，还包括 Bob 的挠率基 $\varphi_A(P_B), \varphi_A(Q_B)$ 的图像。

此辅助信息对于 SIDH 的密钥交换机制至关重要——没有它，Bob 无法计算共享密钥。但是，它也为攻击者提供了以下能力：

1. 通过候选同源路径推送挠率点
2. 构建粘合映射所需的 $(2^{e_A}, 2^{e_A})$ 子群
3. 构建形成 oracle 的维度 2 菱形图

如果没有此挠率点信息，则该攻击不适用。该观察结果导致了 SIDH 变体的开发，这些变体试图隐藏或混淆挠率点图像，但设计安全有效的替代方案仍然是一个积极的研究领域。

泛化和变体

上述简化描述假设：

• 起始曲线是 E0$E_0$ 本身（没有中间同源到特殊曲线）
• 每次迭代恢复单个 3-同源（一次一个 base-3 数字）
• 度数 c=2eA−3eB−i$c = 2^{e_A} - 3^{e_B - i}$ 具有 u2+4v2$u^2 + 4v^2$ 形式

在更通用的攻击中：

• 起始曲线 $E_0$ 可能与具有已知自同态的曲线不同，需要初始同源 $\tau: E0 \to E{\text{start}}$，其中 $E_{\text{start}}$ 具有显式自同态
• 每次迭代可能会一次恢复多个 3-同源（更大的步长，恢复多个 base-3 数字），从而减少总迭代次数，但代价是每次迭代的候选者更多
• 当 $c$ 不具有 $u^2 + 4v^2$ 形式时，辅助同源的构建可能会使用不同的二次形式或更复杂的技术

无论这些变化如何，核心逻辑保持不变：使用维度 2 oracle 一步一步地测试候选边，直到恢复整个秘密路径。

影响和后果

Castryck-Decru 攻击于 2022 年 7 月发布，彻底破坏了 SIDH 的安全性。在 ePrint 上出现预印本后的几小时内，该攻击针对 SIDH 实现进行了实施和验证。该攻击适用于所有标准 SIDH 参数集，并且不能通过简单地增加密钥大小来缓解。

这一进展消除了 SIDH 作为后量子密码学标准化的候选者。该攻击强调了在基于同源的协议中包含辅助信息（挠率点图像）的危险性，从而激发了对替代设计的研究，这些设计要么避免此信息，要么通过其他方式保护它。

致谢

这篇总结紧密遵循并综合了下面列出的三个参考文献中的材料。

• “ 适用于初学者的超奇异同源密钥交换”
• “ 对 SIDH 的有效密钥恢复攻击”
• “ 超奇异同源 Diffie–Hellman 密钥交换”

作者衷心感谢这些著作，感谢它们清晰的符号、精确的事实陈述和具体的算法描述，本文重现并浓缩了这些内容，以便对 SIDH 及其破解进行连贯的、技术上忠实的演练。

• 原文链接： hexens.io/blog/sidh...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～