【TCC 25 论文速递】基于Duplex Sponges的Fiat-Shamir转换及spongefish代码解析
- XPTY
- 发布于 2025-10-23 23:45
- 阅读 719
Alessandro Chiesa和Michele Orrù的论文《A Fiat–Shamir Transformation From Duplex Sponges》为基于duplex sponge的Fiat-Shamir转换提供了严格的理论分析和具体的安全界,并开源了Rust实现库spongefish。
Alessandro Chiesa和Michele Orrù的论文《A Fiat–Shamir Transformation From Duplex Sponges 》(IACR ePrint 2025/536,即将发表于TCC 2025)首次为基于duplex sponge的Fiat-Shamir转换提供了严格的理论分析和具体的安全界,同时开源了Rust实现库spongefish。

论文的理论贡献包括:揭示了不可区分性(indifferentiability,注意不是indistinguishability!)不足以建立非交互式论证的知识可靠性和零知识性。通过白盒分析duplex sponge的内部结构获得紧致的安全界,避免了黑箱组合带来的松散性。这提醒研究者在依赖组合定理时需要谨慎评估安全性损失。
过去几十年里,密码学实践与理论存在不一致:理论研究主要关注基于压缩函数的规范Fiat-Shamir转换(使用多个独立的随机预言机),但实际系统几乎都采用基于置换函数的sponge构造,如Keccak-f和Poseidon。从merlin、bulletproofs到arkworks、gnark,超过12个主流零知识证明库都使用了duplex sponge模式,但这些实践长期缺乏严格的理论分析。本文填补了这一空白,证明了实践方法的理论合理性,并为参数选择提供了具体指导。
spongefish库将理论成果转化为生产就绪的代码。从工程角度,spongefish通过trait抽象、类型安全、编解码器机制和域分隔符等设计,将密码学理论转化为易用的API。代码中的安全细节包括:不实现Clone trait防止状态泄露、使用Zeroize自动清零敏感数据、通过类型系统强制协议正确性等。
Sponge构造与Duplex模式
要理解基于Duplex Sponges的Fiat-Shamir转换,首先需要深入了解sponge构造这一优雅的密码学设计。Sponge函数由Bertoni等人在2007年提出,现已成为SHA-3标准(Keccak)的基础。这类函数具有有限的内部状态,可以接受任意长度的输入并产生任意长度的输出,展现了罕见的灵活性和通用性。Sponge构造基于一个固定长度的置换函数$p$,该函数操作$b$位状态,状态被分为两个部分:速率(rate)$r$位和容量(capacity)$c$位,满足$b = r + r$。速率部分用于输入和输出数据,而容量部分永不直接受输入影响,也不在输出阶段直接暴露,这种分离是sponge构造安全性的关键。
Sponge函数的工作流程分为两个阶段:吸收阶段和挤压阶段。在吸收阶段,输入消息首先通过填充规则填充并切分为$r$位的块,状态初始化为全零,然后每个输入块与状态的前$r$位进行XOR运算,接着对整个$b$位状态应用置换函数$p$,重复这一过程直到所有输入块被处理完毕。形式化地表示为$s = p(s \oplus (P_i | 0^c))$,其中$P_i$是第$i$个输入块。在挤压阶段,输出状态的前$r$位作为输出块,如需更多输出则再次应用置换函数并输出前$r$位,重复直到获得所需长度的输出。这种设计的安全性依赖于容量$c$,对于$c$位容量的Sponge构造,可以抵抗复杂度为$2^{c/2}$的通用攻击,攻击成功概率的上界为$N^2/2^{c+1}$,其中$N$是对底层置换的查询次数。Bertoni等人在EUROCRYPT 2008证明了Sponge构造的不可区分性,这意味着攻击Sponge函数等价于区分底层置换与随机置换。
Duplex构造是Sponge的"姊妹构造",由Bertoni等人在2011年提出,专门设计用于需要交替输入输出的场景。与标准Sponge的无状态、严格分离吸收和挤压阶段不同,Duplex构造是有状态的,维护跨调用的内部状态,每次调用可以同时接收输入并产生输出,这使它非常适合模拟全双工通信。Duplex的核心操作是duplexing,其流程为:首先将输入$\sigma$填充为$r$位块$P$,然后将$P$与状态的率部分进行XOR运算(即$\text{state} = \text{state} \oplus (P | 0^{b-r})$),接着应用置换函数$p$,最后返回状态的前$\ell$位作为输出($\ell \leq r$)。这个操作的关键性质是:Duplex对象在调用之间保持$b$位状态,并且该状态等价于sponge函数吸收所有历史输入后的状态,这意味着每次duplexing调用相当于对迄今为止所有输入的sponge函数调用,因此Duplex构造继承了Sponge的安全性保证。
Duplex模式的优势在实践应用中充分得以体现。在认证加密领域,SpongeWrap方案实现了单遍处理,每个数据块仅需一次置换调用,同时实现加密和认证而无需两次遍历,并且原生支持中间标签(intermediate tags)。在伪随机数生成器方面,Duplex支持通过feed操作添加熵源,通过fetch操作获取随机比特,并提供前向安全性:即使当前状态泄露也不会影响过去生成的随机数。而对于Fiat-Shamir转换这一本文的核心应用,Duplex模式天然适合模拟交互式协议:吸收证明者消息,挤压验证者挑战,状态自动维护完整的交互历史。相比标准Sponge,Duplex以单遍操作最小化了置换调用次数,展现了更高的效率和灵活性,同时保持了可证明的安全性。
Fiat-Shamir转换的理论基础与实践挑战
Fiat-Shamir启发式是密码学中的一项基础性技术,由Amos Fiat和Adi Shamir在1986年提出,用于将交互式知识证明转换为数字签名,更广泛地说,它将公开抛币(public-coin)交互式证明转换为非交互式证明。交互式证明的典型结构是Σ-协议,包含三个步骤:首先证明者生成随机值并计算承诺发送给验证者,然后验证者发送均匀随机选择的挑战,最后证明者基于承诺和挑战计算响应。Fiat-Shamir转换的核心思想是用哈希函数$H$替代验证者的随机挑战,即挑战$c = H(\text{承诺}, \text{陈述})$,这样证明者可以自己计算挑战,无需与验证者交互。在随机预言机模型(Random Oracle Model, ROM)中,哈希函数被建模为理想化的密码学函数,对每个唯一输入返回均匀随机的输出,对相同输入总是返回相同输出,这个理论框架尽管存在一些已知的理论局限性(存在在ROM中安全但任何具体实例化都不安全的方案),但在实践中已被广泛接受并经受了几十年的考验。
然而,传统的规范Fiat-Shamir转换在实践中面临两个根本性问题。第一个问题是设计不匹配:理论上的规范转换对$k$轮协议使用$k$个独立的随机预言机,每个随机预言机的形式为$f_i: \mathbb{F}2^n \times \mathcal{M}{P,1} \times \ldots \times \mathcal{M}{P,i} \to \mathcal{M}{V,i}$,其中$\mathcal{M}{P,i}$和$\mathcal{M}{V,i}$分别是第$i$轮证明者和验证者的消息空间。但实际的密码学哈希函数是基于固定长度块的压缩函数,与这种灵活的消息空间映射存在根本性的不匹配。第二个问题更为严重:二次爆炸 。由于第$i$个查询包含在第$(i+1)$个查询中,即验证者在生成第$i+1$个挑战时需要哈希所有前$i$轮的消息,总查询大小达到$k \cdot |\mathbb{X}| + \sum_{i \in [k]} (k - i + 1) \cdot |\alpha_i| = \Omega(k^2)$,其中$\mathbb{X}$是实例,$\alpha_i$是第$i$轮证明者消息。这种二次复杂度在多轮协议中会导致显著的性能损失。
为了解决这些问题,实践中出现了哈希链(hash-chain)变体(HCFS) ,它使用$k$个不同的随机预言机,其中第一个为$f_1: \mathbb{F}2^n \times \mathcal{M}{P,1} \to \mathcal{M}_{V,1}$,而对于$i = 2, \ldots, k$则使用$fi: \mathcal{M}{V,i-1} \times \mathcal{M}{P,i} \to \mathcal{M}{V,i}$,即每个挑战只依赖于前一个挑战和当前轮的证明者消息。但这种方法仍然存在问题:预言机依赖于特定的消息空间,且在实践中并未被广泛采用。事实上,Chiesa和Orrù的研究发现了一个令人震惊的现象:从1987年到2025年的近40年间,尽管存在规范和哈希链这两种理论上完善的方法,实践中的主流实现——包括zkcrypto的merlin、dalek-cryptography的bulletproofs、arkworks-rs的crypto-primitives、ConsenSys的gnark、starkware-libs的stwo、succinctlabs的plonky3、iden3的snarkjs等超过12个生产级密码学库——几乎都没有使用规范或哈希链变体,而是采用了基于置换函数(如Keccak-f和Poseidon)的duplex sponge构造,但这些广泛部署的实现长期缺乏严格的理论分析。

论文核心贡献:Duplex Sponge Fiat-Shamir转换的形式化分析
Chiesa和Orrù的论文最重要的贡献在于为实践中的duplex sponge Fiat-Shamir转换提供了首个严格的理论分析和具体的安全界。论文定义了DSFS[IP](Duplex Sponge Fiat-Shamir)协议,对于一个Σ-协议,转换过程如下:证明者首先通过$\text{Absorb}_p(\mathbb{X})$初始化并吸收实例$\mathbb{X}$,然后生成第一轮消息$\alpha_1$并执行$\text{Absorb}_p(\alpha_1)$,接着通过$\rho_1 \leftarrow \text{Squeeze}_p(\ell^{(1)})$获取验证者挑战$\rho_1$,最后生成第二轮消息$\alpha_2$并输出证明$\pi := (\alpha_1, \alpha_2)$。验证者的过程类似:解析证明$\pi = (\alpha_1, \alpha_2)$,依次执行$\text{Absorb}_p(\mathbb{X})$和$\text{Absorb}_p(\alpha_1)$,通过$\rho \leftarrow \text{Squeeze}_p(\ell^{(1)})$重新计算挑战,最后验证$V(\mathbb{X}, \alpha_1, \alpha_2, \rho)$。对于$k$轮协议,这个duplexing操作重复$k$次,每轮包含吸收证明者消息和挤压验证者挑战两个步骤。
这种构造的效率优势是显著的。对于$k$轮协议,吸收实例$\mathbb{X}$需要$\lceil |\mathbb{X}|/r \rceil$次置换调用,而对每轮$i$,吸收证明者消息$\alpha_i$需要$\lceil |\alpha_i|/r \rceil$次调用,挤压验证者挑战$\rho_i$需要$\lceil |\rhoi|/r \rceil$次调用,总调用次数为$\sum{i \in [k]} (\lceil |\alpha_i|/r \rceil + \lceil |\rho_i|/r \rceil)$,这是关于轮数$k$的线性复杂度,而规范Fiat-Shamir转换的复杂度为$O(k \cdot n + k^2 \cdot m)$(其中$m$是平均消息大小),是二次的。这意味着对于典型的3到5轮协议,DSFS可以节省40%到60%的哈希计算量,这在递归零知识证明系统中尤为关键,因为每次哈希调用都需要在证明电路中进行验证。
论文的另一个重大理论贡献是揭示了不可区分性(indifferentiability)的不充分性。长期以来,密码学界认为如果一个构造具有不可区分性,那么它可以安全地替代随机预言机。但Chiesa和Orrù证明了,对于Fiat-Shamir转换的知识可靠性和零知识性,不可区分性是不够的。具体而言,如果使用不可区分性结合混合论证来证明安全性,会导致误差界限为$|\mathfrak{tr}{\text{std}}| \cdot \varepsilon{\text{ind}} \leq t \cdot O(t^2/|\Sigma|^c)$,其中$t$是对手对置换的查询次数,$|\Sigma|$是置换域的大小,$c$是容量。这产生了三次加性误差$O(t^3/|\Sigma|^c)$,在实践中过于松散。论文通过直接分析duplex sponge的内部结构,避免了这种松散性,获得了更紧的安全界。
论文提供的知识可靠性定理(非正式版本)表明,在理想置换模型中,DSFS[IP]的知识可靠性满足:
$$ \varepsilon{\text{ksnd}} \leq \varepsilon{\text{srsnd}} + O\left(\frac{t^2}{|\Sigma|^c}\right) + O(t) \cdot \max{i \in [k]} \varepsilon{\text{cdc},i} $$
其中$\varepsilon{\text{srsnd}}$是交互式证明的状态恢复可靠性(state-restoration soundness) ,$t$是对手对置换$p$的查询次数,$c$是容量,$\varepsilon{\text{cdc},i}$是第$i$个编解码器的偏差。状态恢复可靠性是比传统轮次(Round-by-Round可靠性更强的性质,要求即使对手可以"倒带(rewinding)"协议状态,仍然无法伪造证明。这个界的关键特点是对$t$的依赖是二次的而非三次,相比使用不可区分性的方法减少了一个因子$t$。对于零知识性,论文证明了在显式可编程随机预言机模型中:
$$ \varepsilon{\text{zk}} \leq \varepsilon{\text{hvzk}} + O\left(\frac{t}{\Sigma^{\min(c,\delta)}}\right) + \sum{i \in [k]} \varepsilon{\text{cdc},i} $$
其中$\varepsilon{\text{hvzk}}$是交互式证明的诚实验证者零知识性,$\delta$是隐私参数。这里对$t$的依赖是线性的,同样比使用不可区分性的二次依赖改进了一个因子$t$。这些具体的安全界为实践中的参数选择提供了明确指导:对于128位安全性,容量$c$应至少为256位以抵抗生日攻击,编解码器偏差$\varepsilon{\text{cdc}}$应小于$2^{-128}$,并且需要限制攻击者的查询次数$t \ll 2^{c/2}$,在实践中通常取$t \approx 2^{64}$。
论文的证明策略采用归约方法,核心思想是寻找归约函数$\text{ReduceP}$和$\text{ReduceT}$,使得基于理想置换的DSFS攻击者可以转换为针对规范Fiat-Shamir的攻击者,同时保持transcript的有效性。具体地,论文证明了以下两个世界在计算上不可区分:一个是对手在理想置换下攻击DSFS,另一个是归约的对手在随机预言机下攻击规范FS。归约的加性误差由置换查询次数决定,通过精细分析duplex sponge的内部状态转换和查询依赖关系,论文避免了不可区分性带来的额外误差放大。这种直接分析方法要求更深入地理解duplex构造的工作机制,但换来的是实践中可用的紧致安全界。

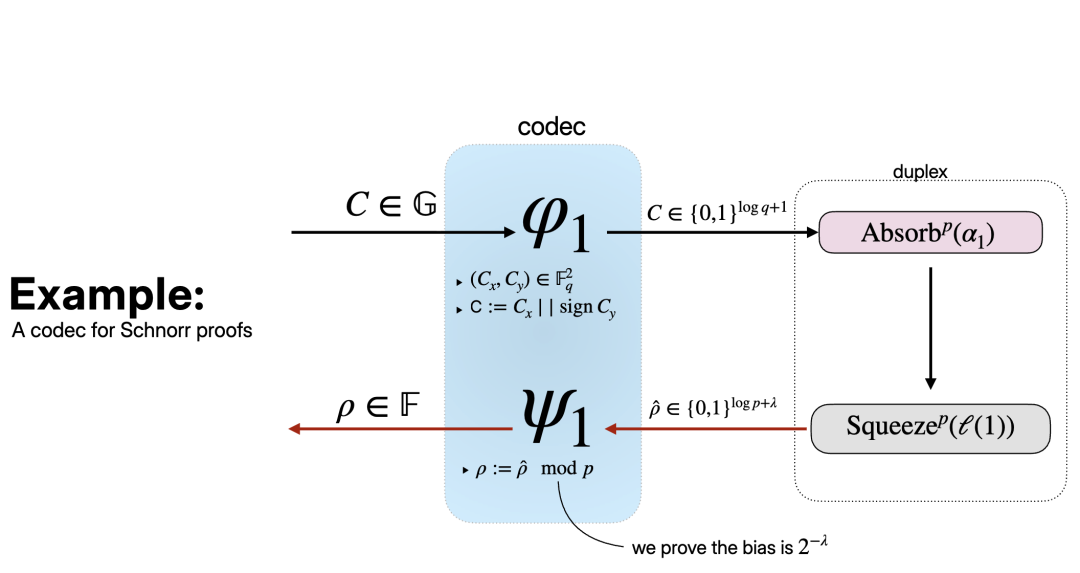
论文还引入了编解码器(codecs) 的概念,用于处理证明者/验证者消息空间与置换域之间的映射。编码映射$\phii: \mathcal{M}{P,i} \to \Sigma^$负责在absorb操作时将证明者消息转换为置换域的元素,必须是单射(injective)以确保不同消息映射到不同的状态。解码映射$\psi_i: \Sigma^ \to \mathcal{M}_{V,i}$负责在squeeze操作时将置换的输出转换为验证者挑战,必须允许原像采样(preimage sampling),这对模拟器构造零知识证明至关重要,并且$\psi_i \circ \mathcal{U}$应该$\varepsilon$-接近均匀分布($\varepsilon$-biased)。以Schnorr协议为例,在squeeze阶段生成挑战$\rho \in \mathbb{F}_q$时,首先从sponge提取$\hat{\rho} \in {0,1}^{\log q + \lambda}$,然后设置$\rho := \hat{\rho} \mod q$,这种方法的偏差为$2^{-\lambda}$。在absorb阶段吸收承诺点$C \in \mathbb{G}$时,提取坐标$(C_x, C_y) \in \mathbb{F}_q^2$,编码为$C := C_x | \text{sign}(C_y) \in {0,1}^{\log q + 1}$,这种点压缩方案在保持唯一性的同时最小化了编码长度。
arkworks spongefish代码库解析
spongefish是Chiesa和Orrù论文的官方Rust实现,提供与置换函数无关的通用API。项目采用Rust workspace架构,包含核心库spongefish、工作量证明扩展spongefish-pow,以及正在开发的Anemoi和Poseidon哈希函数实现。
软件栈结构
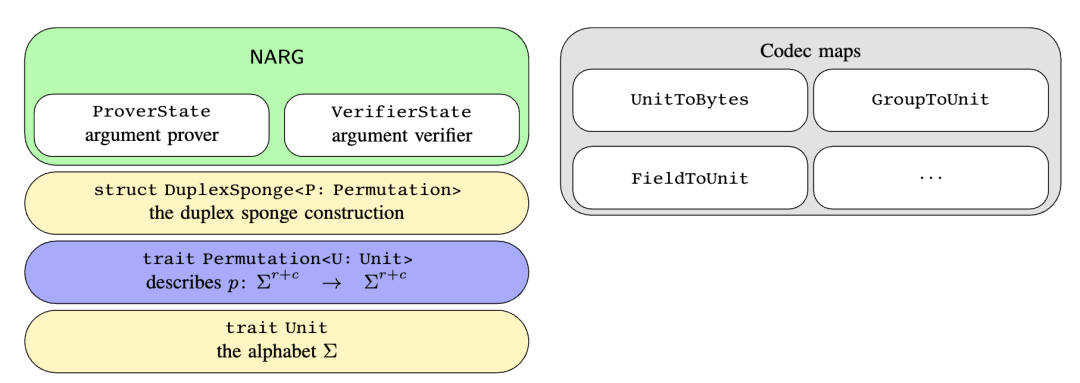
spongefish的软件栈分为四层,从底层到顶层依次为:
1. 基础层:trait定义
-
Unittrait:定义置换的字母表$\Sigma$,要求类型具有编译时已知的固定大小(Sized)、可复制(Clone)、安全删除(zeroize::Zeroize)、序列化/反序列化(通过write和read函数) -
Permutation<U: Unit>trait:描述置换函数$p: \Sigma^{r+c} \to \Sigma^{r+c}$,其中$r$是速率(Permutation::R),$c$是容量(Permutation::C),仅需实现permute方法。该trait公开暴露,允许使用任意置换函数。论文提供了基于keccak crate的Keccak实现和基于arkworks库的Poseidon实现。
2. Duplex Sponge层
实现DuplexSponge<P: Permutation>结构,基于给定的任意置换P实现覆写模式的duplex构造(论文Construction 3.3):
// DuplexSponge核心方法
pub fn absorb(&mut self, input: &[Unit]);
pub fn squeeze(&mut self, output: &mut [Unit]); 覆写模式的absorb直接将输入复制到state的rate部分,而非XOR:
fn absorb(&mut self, input: &[Unit]) {
let chunk_size = min(self.rate, input.len() - offset);
self.state[0..chunk_size].copy_from_slice(&input[offset..offset + chunk_size]);
self.permutation.permute(&mut self.state);
} 3. NARG层:Argument Prover和Verifier
在duplex sponge实现之上,构建两个结构来实现论文Construction 4.3中的论证证明者和验证者:
-
ProverState<P: Permutation>:包含NARG证明者状态,允许absorb/squeeze单元,内部更新论证字符串。该结构包含:(i) 当前sponge状态,(ii) 迄今序列化的NARG字符串,(iii) 论证证明者的私有币。设计特性:- 不实现
Clone和Copytrait,防止证明者状态在执行期间被克隆(状态中包含私有随机性) - NARG字符串仅包含已纳入Fiat-Shamir转换的证明者消息
- 不实现
VerifierState<P: Permutation>:实现NARG验证者,接受论证字符串作为输入,在验证者执行期间,将字符串反序列化为证明者消息(作为单元),并将其馈送到duplex sponge以导出IP验证者消息
利用Rust的类型安全特性防止误用:证明者状态在执行期间不可克隆,NARG字符串仅包含包含在Fiat-Shamir转换中的证明者消息。
4. Codecs层:扩展trait
通过extension traits添加从任意域absorb和squeeze的能力。codecs子模块实现以下扩展:
-
FieldToUnit<F>extension:提供编码映射$\varphi$,将证明者消息从域F转换为单元U(置换字母表)。支持的域类型:ark-ff(arkworks-rs/algebra)或ff(zkcrypto/ff)pub trait FieldToUnit<F> {
fn field_to_units(field_elem: &F) -> Vec<Self>;
} -
UnitToField<F>extension:提供可忽略偏差的映射$\psi$,将均匀分布的单元发送到(几乎)均匀分布的域F元素(遵循Lemma C.1)。支持字节单元(U=u8)和域元素单元(U=F),为arkworks和zkcrypto/ff实现pub trait UnitToField<F> {
fn units_to_field(units: &[Self]) -> F;
} -
GroupToUnit<G>extension:提供编码映射$\varphi$,压缩并序列化椭圆曲线群元素为单元。支持arkworks-rs/algebra和zkcrypto/ff的椭圆曲线类型pub trait GroupToUnit<G> {
fn group_to_units(group_elem: &G) -> Vec<Self>;
} -
UnitToBytesextension:允许将单元(从duplex sponge挤压)映射为字节。对于二进制单元,实现是平凡的(依赖于挤压域原生单元)。对于代数置换,遵循Lemma C.1确保挤压的IP验证者消息可忽略地接近均匀分布
域分隔符(Domain Separator)
域分隔符是UTF-8编码的字符串包装器,用于唯一标识协议及其交互模式:
let domain_separator = DomainSeparator::<DefaultHash>::new("example-protocol")
.absorb(1, "prover_message")
.squeeze(16, "verifier_challenge"); 标记被编码为特定格式的字符串,如"example-protocol\0A1prover_message\0S16verifier_challenge"(\0是NULL字节分隔符,A表示Absorb,S表示Squeeze),用于生成初始化向量(IV),确保不同协议使用不同的初始状态,防止跨协议攻击。
ProverState和VerifierState使用示例
ProverState基本用法 :
// 创建证明者状态
let mut prover_state = domain_separator.to_prover_state();
// 发送消息(触发absorb)
prover_state.add_bytes(&[0x42])?;
// 接收挑战(触发squeeze)
let mut challenge = [0u8; 16];
prover_state.fill_challenge_bytes(&mut challenge)?;
// 生成私有随机值(绑定到transcript)
let k = G::ScalarField::rand(prover_state.rng());
// 获取NARG字符串
let transcript = prover_state.narg_string(); VerifierState基本用法 :
// 从NARG字符串创建验证者状态
let mut verifier_state = domain_separator.to_verifier_state(&transcript);
// 读取证明者消息
let [first_message] = verifier_state.next_bytes()?;
// 生成挑战(重新执行相同的duplex操作)
let challenge = verifier_state.challenge_bytes::<16>()?; 验证者重新执行与证明者相同的duplex操作序列,得到相同的挑战值。如果NARG字符串不一致,验证自动失败。
Schnorr协议完整实现
证明知道$x$使得$X = xG$:
// 证明者
let k = G::ScalarField::rand(prover_state.rng()); // 私有随机性
let K = base * k;
prover_state.add_points(&[K])?; // 发送承诺(absorb)
let [c] = prover_state.challenge_scalars()?; // 接收挑战(squeeze)
let r = k + c * secret;
prover_state.add_scalars(&[r])?; // 发送响应(absorb)
let proof = prover_state.narg_string(); // 获取证明
// 验证者
let mut verifier_state = domain_separator.to_verifier_state(&proof);
let [K] = verifier_state.next_points()?; // 读取承诺
let [c] = verifier_state.challenge_scalars()?; // 重新计算挑战
let [r] = verifier_state.next_scalars()?; // 读取响应
assert_eq!(base * r, K + public * c); // 验证等式 add_points、challenge_scalars、add_scalars等方法通过codecs扩展trait自动处理编解码。
编解码器实现细节
有限域元素编解码 :
- 编码(
FieldToUnit):将域元素的规范表示序列化为字节 - 解码(
UnitToField):采样$256 + \lambda$比特然后模$q$,统计距离$2^{-\lambda}$($\lambda$通常取128)
椭圆曲线点压缩 (GroupToUnit):
- 存储:$x$坐标+$y$的符号位
- 恢复:求解$y = \pm\sqrt{x^3 + ax + b}$,根据符号位选择正确的$y$
- 示例:BLS12-381曲线点从~64字节压缩到~33字节
字节映射 (UnitToBytes):* 二进制单元:直接挤压域原生单元
- 代数置换:遵循Lemma C.1确保可忽略偏差
安全性考虑
- 初始化 :域分隔符生成的IV确保不同协议使用不同初始状态
- 状态转换 :置换函数的双射性保证状态演化可逆,容量部分提供生日界限安全性
- 参数选择 (128位安全性):容量$c \geq 256$位,编解码器偏差$< 2^{-128}$,查询次数$t \approx 2^{64}$
- 内存安全 :使用
zeroizecrate自动清零敏感数据,ProverState的Drop实现自动清零内部状态 - 类型安全 :通过Rust类型系统防止状态克隆、确保NARG字符串完整性
与arkworks生态集成
spongefish是arkworks旧sponge库的替代品(旧库已归档,功能移至crypto-primitives)。通过提供与arkworks类型兼容的编解码器和API,现有零知识证明代码可以轻松迁移。支持:
- 有限域算术(ark-ff)
- 椭圆曲线群(ark-ec)
- 序列化支持(ark-serialize)
开放问题与未来研究方向
论文最后提出了三个重要的研究问题,为未来工作指明了方向。首先是支持传统哈希函数 :能否将旧的基于压缩函数的哈希(如SHA-256)包装为相同的Absorb/Squeeze API,这对于需要兼容现有系统的场景很重要。其次是强不可区分性 :正在进行的研究试图开发一种不可区分性的变体,足以保证知识可靠性和零知识性,这可能简化未来的安全性证明并提供更模块化的分析框架。第三是通用可组合性 :能否在全局"理想置换"模型中证明UC安全性,类似于全局随机预言机模型(GROM),这对于构建大型密码系统的安全性论证至关重要。
此外,标准化工作也在进行中。IETF正在制定Fiat-Shamir转换的标准草案,spongefish的实现和论文的理论分析为标准化提供了重要参考。随着零知识证明技术在区块链、隐私计算、可验证计算等领域的广泛应用,基于Duplex Sponges的Fiat-Shamir转换必将发挥越来越重要的作用,而Chiesa和Orrù的工作为这一技术的理论基础和工程实践都奠定了坚实的基石。
- 本文转载自: mp.weixin.qq.com/s/7oyFa... , 如有侵权请联系管理员删除。
- 转载
- 学分: 2
- 分类: 密码学
- 标签: Fiat-Shamir转换 duplex sponge 知识证明 零知识证明 密码学 Rust语言
- ZK编年史:哈希登场 67 浏览
- 以太坊协议研究学习小组 - 2026 启动 134 浏览
- 神奇的 Zig、C 和 OpenSSL 168 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 300 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 252 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 332 浏览
- Shamir份额的魔力:BLS门限签名 411 浏览
- Zcash:比特币遗忘的隐私 406 浏览
- ZK编年史:计算模型 282 浏览
- lambdaworks 2026 年更新路线图和优先级 334 浏览
- 2026年构建机构级DeFi平台真正需要什么 825 浏览
- zkMesh:2026年1月回顾 423 浏览

