Uniswap V3 开发指南
流动性计算
- Jeiwan
- 发布于 2025-10-02 10:45
- 阅读 37
没有流动性就不可能进行交易,为了完成我们的首次 swap,我们需要将一些流动性放入池合约中。以下是向池合约添加流动性时需要了解的内容:
- 价格范围。作为流动性提供者,我们希望在特定的价格范围内提供流动性,并且它只会在这个范围内使用。
- 流动性数量,即两种 token 的数量。我们需要将这些数量转移到池合约中。
这里,我们将手动计算这些,但是在后面的章节中,将由一个合约来完成。让我们从价格范围开始。
价格范围计算
回想一下,在 Uniswap V3 中,整个价格范围被划分为多个 tick:每个 tick 对应一个价格,并有一个索引。在我们的第一个池实现中,我们将以每个 1 ETH 兑换 \$5000 的价格购买 ETH。购买 ETH 会从池中移除一定数量的 ETH,并将价格略微推高至 \$5000 以上。我们希望在包含此价格的范围内提供流动性。并且我们希望确保最终价格保持在这个范围内(我们将在后面的里程碑中进行多范围 swap)。
我们需要找到三个 tick:
- 当前的 tick 将对应当前价格(1 ETH 兑换 5000 USDC)。
- 我们提供流动性的价格范围的下限和上限。设最低价格为 \$4545,最高价格为 \$5500。
从理论介绍中,我们知道:
$$\sqrt{P} = \sqrt{\frac{y}{x}}$$
由于我们已经同意使用 ETH 作为 $x$ 储备,USDC 作为 $y$ 储备,因此每个 tick 的价格为:
$$\sqrt{P_c} = \sqrt{\frac{5000}{1}} = \sqrt{5000} \approx 70.71$$
$$\sqrt{P_l} = \sqrt{\frac{4545}{1}} \approx 67.42$$
$$\sqrt{P_u} = \sqrt{\frac{5500}{1}} \approx 74.16$$
其中 $P_c$ 是当前价格,$P_l$ 是范围的下限,$P_u$ 是范围的上限。
现在,我们可以找到对应的 tick。我们知道价格和 tick 通过这个公式连接:
$$\sqrt{P(i)}=1.0001^{\frac{i}{2}}$$
因此,我们可以通过以下方式找到 tick $i$:
$$i = log_{\sqrt{1.0001}} \sqrt{P(i)}$$
此公式中的平方根抵消了,但是由于我们正在使用 $\sqrt{p}$,因此我们需要保留它们。
让我们找到这些 tick:
- 当前 tick:$ic = log{\sqrt{1.0001}} 70.71 = 85176$
- 较低的 tick:$il = log{\sqrt{1.0001}} 67.42 = 84222$
- 较高的 tick:$iu = log{\sqrt{1.0001}} 74.16 = 86129$
为了计算这些,我使用了 Python:
import math def price_to_tick(p): return math.floor(math.log(p, 1.0001)) price_to_tick(5000) > 85176
这就是价格范围计算的全部内容!
这里最后要注意的是,Uniswap 使用 Q64.96 number 来存储 $\sqrt{P}$。 这是一个定点数,其中整数部分有 64 位,小数部分有 96 位。 在我们上面的计算中,价格是浮点数:70.71、67.42 和 74.16。我们需要将它们转换为 Q64.96。幸运的是,这很简单:我们需要将数字乘以 $2^{96}$(Q 数是一个二进制定点数,所以我们需要将我们的小数数字乘以 Q64.96 的基数,即 $2^{96}$)。我们会得到:
$$\sqrt{P_c} = 5602277097478614198912276234240$$
$$\sqrt{P_l} = 5314786713428871004159001755648$$
$$\sqrt{P_u} = 5875717789736564987741329162240$$
在 Python 中:
q96 = 2**96 def price_to_sqrtp(p): return int(math.sqrt(p) * q96) price_to_sqrtp(5000) > 5602277097478614198912276234240请注意,我们在转换为整数之前进行乘法运算。 否则,我们将失去精度。
Token 数量计算
下一步是决定我们要将多少 token 存入池中。 答案是越多越好。 数量没有严格定义,我们可以存入足够的数量,以便在不使当前价格离开我们投入流动性的价格范围的情况下购买少量 ETH。 在开发和测试期间,我们将能够铸造任意数量的 token,因此获得我们想要的数量不是问题。
对于我们的首次 swap,让我们存入 1 ETH 和 5000 USDC。
回想一下,当前池储备的比例表示当前现货价格。 因此,如果我们想将更多 token 放入池中并保持相同的价格,则数量必须成比例,例如:2 ETH 和 10,000 USDC; 10 ETH 和 50,000 USDC 等。
流动性数量计算
接下来,我们需要根据我们将要存入的数量来计算 $L$。 这是一个棘手的部分,所以请坚持住!
从理论介绍中,你还记得: $$L = \sqrt{xy}$$
但是,此公式适用于无限曲线 🙂 但是我们想将流动性投入到有限的价格范围内,这只是该无限曲线的一部分。 我们需要专门为我们将要存入流动性的价格范围计算 $L$。 我们需要更高级的计算。
要计算价格范围的 $L$,让我们看一下我们之前讨论过的一个有趣的事实:价格范围可能会耗尽。 可以从价格范围中购买一种 token 的全部数量,并使池中仅剩下另一种 token。
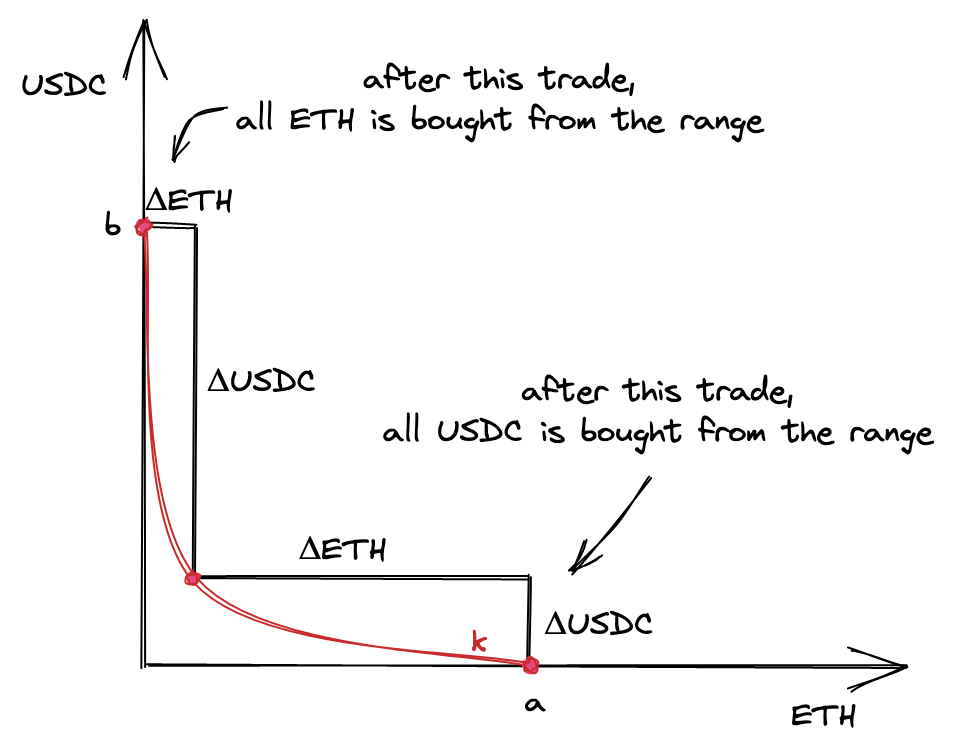
在 $a$ 和 $b$ 点,该范围内只有一种 token:$a$ 点的 ETH 和 $b$ 点的 USDC。
话虽如此,我们想找到一个 $L$,该 $L$ 将允许价格移动到任一点。 我们希望有足够的流动性使价格达到价格范围的任一边界。 因此,我们希望基于 $\Delta x$ 和 $\Delta y$ 的最大数量来计算 $L$。
现在,让我们看看边缘的价格是多少。 当从池中购买 ETH 时,价格会上涨; 当购买 USDC 时,价格会下跌。 回想一下,价格是 $\frac{y}{x}$。 因此,在 $a$ 点,价格是该范围内的最低价格; 在 $b$ 点,价格是最高价格。
实际上,这些点上的价格没有定义,因为池中只有一个储备,但是我们需要在此处理解的是 $b$ 点附近的价格高于起始价格,而 $a$ 点的价格低于起始价格。
现在,将上图中的曲线分为两段:一段在起点的左侧,一段在起点的右侧。 我们将计算两个 $L$,每个段一个。 为什么? 因为池的两个 token 中的每一个都有助于任一段:左段完全由 token $x$ 组成,右段完全由 token $y$ 组成。 这是因为在 swap 期间,价格会向任一方向移动:它是增长还是下降。 为了使价格移动,只需要任一 token 即可:
- 当价格上涨时,swap 只需要 token $x$(我们正在购买 token $x$,因此我们只想从池中获取 token $x$);
- 当价格下跌时,swap 只需要 token $y$。
因此,曲线段中当前价格左侧的流动性仅由 token $x$ 组成,并且仅从提供的 token $x$ 的数量计算得出。 类似地,曲线段中当前价格右侧的流动性仅由 token $y$ 组成,并且仅从提供的 token $y$ 的数量计算得出。
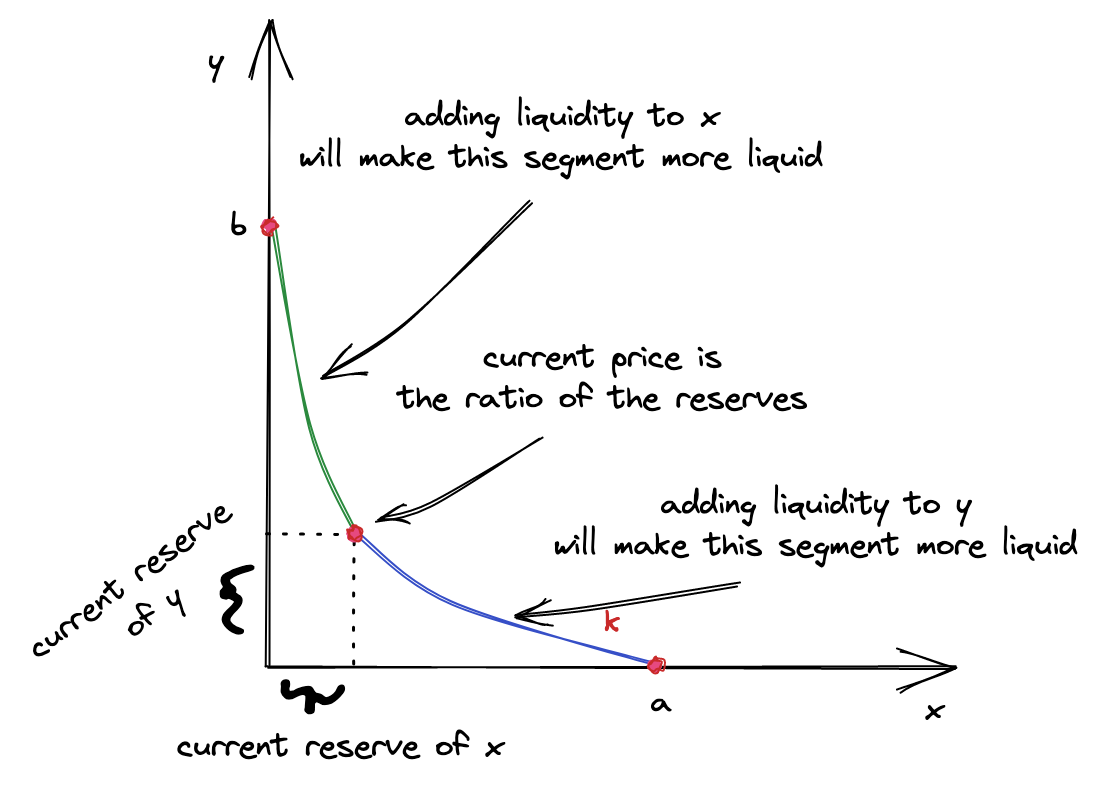
这就是为什么在提供流动性时,我们要计算两个 $L$ 并选择其中之一。 哪一个? 较小的一个。 为什么? 因为较大的一个已经包含了较小的一个! 我们希望新的流动性均匀地分布在曲线上,因此我们希望在当前价格的左侧和右侧添加相同的 $L$。 如果我们选择较大的一个,则用户将需要提供更多的流动性来补偿较小的数量的不足。 这当然是可行的,但是这会使智能合约更加复杂。
较大的 $L$ 的余数会发生什么? 好吧,没什么。 在选择较小的 $L$ 后,我们可以简单地将其转换为导致较大 $L$ 的 token 的较小数量——这将向下调整它。 之后,我们将拥有会导致相同 $L$ 的 token 数量。
我需要你关注的最后一个细节是:新的流动性不得改变当前价格。 也就是说,它必须与当前储备金的比例成比例。 这就是为什么两个 $L$ 可能不同的原因——当比例未保留时。 我们选择小 $L$ 来重新建立比例。
我希望在我们用代码实现之后,这将更有意义! 现在,让我们看一下公式。
让我们回顾一下如何计算 $\Delta x$ 和 $\Delta y$:
$$\Delta x = \Delta \frac{1}{\sqrt{P}} L$$ $$\Delta y = \Delta \sqrt{P} L$$
我们可以通过用实际价格替换 delta P 来扩展这些公式(我们从上面知道它们):
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$
$P_a$ 是 $a$ 点的价格,$P_b$ 是 $b$ 点的价格,$P_c$ 是当前价格(请参见上图)。 请注意,由于价格计算为 $\frac{y}{x}$(即,$x$ 以 $y$ 计价的价格),因此 $b$ 点的价格高于当前价格和 $a$ 点的价格。 $a$ 点的价格是三者中最低的。
让我们从第一个公式中找到 $L$:
$$\Delta x = (\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}}) L$$ $$\Delta x = \frac{L}{\sqrt{P_c}} - \frac{L}{\sqrt{P_b}}$$ $$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$
从第二个公式: $$\Delta y = (\sqrt{P_c} - \sqrt{P_a}) L$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
因此,这是我们的两个 $L$,每个段各一个:
$$L = \Delta x \frac{\sqrt{P_b} \sqrt{P_c}}{\sqrt{P_b} - \sqrt{P_c}}$$ $$L = \frac{\Delta y}{\sqrt{P_c} - \sqrt{P_a}}$$
现在,让我们将先前计算的价格代入其中:
$$L = \Delta x \frac{\sqrt{P_b}\sqrt{P_c}}{\sqrt{P_b}-\sqrt{P_c}} = 1 ETH \frac{5875... 5602...}{5875... - 5602...}$$
转换为 Q64.96 后,我们得到:
$$L = 1519437308014769733632$$
对于另一个 $L$: $$L = \frac{\Delta y}{\sqrt{P_c}-\sqrt{P_a}} = \frac{5000USDC}{5602... - 5314...}$$ $$L = 1517882343751509868544$$
在这两个中,我们将选择较小的一个。
在 Python 中:
sqrtp_low = price_to_sqrtp(4545) sqrtp_cur = price_to_sqrtp(5000) sqrtp_upp = price_to_sqrtp(5500) def liquidity0(amount, pa, pb): if pa > pb: pa, pb = pb, pa return (amount * (pa * pb) / q96) / (pb - pa) def liquidity1(amount, pa, pb): if pa > pb: pa, pb = pb, pa return amount * q96 / (pb - pa) eth = 10**18 amount_eth = 1 * eth amount_usdc = 5000 * eth liq0 = liquidity0(amount_eth, sqrtp_cur, sqrtp_upp) liq1 = liquidity1(amount_usdc, sqrtp_cur, sqrtp_low) liq = int(min(liq0, liq1)) > 1517882343751509868544
再次计算 Token 数量
由于我们选择了要存入的数量,因此数量可能不正确。 我们不能在任何价格范围内存入任何数量; 流动性数量需要沿着我们存入的价格范围的曲线均匀分布。 因此,即使使用者选择了数量,合约也需要重新计算它们,并且实际数量会略有不同(至少由于四舍五入)。
幸运的是,我们已经知道了公式:
$$\Delta x = \frac{L(\sqrt{P_b} - \sqrt{P_c})}{\sqrt{P_b} \sqrt{P_c}}$$ $$\Delta y = L(\sqrt{P_c} - \sqrt{P_a})$$
在 Python 中:
def calc_amount0(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * q96 * (pb - pa) / pa / pb) def calc_amount1(liq, pa, pb): if pa > pb: pa, pb = pb, pa return int(liq * (pb - pa) / q96) amount0 = calc_amount0(liq, sqrtp_upp, sqrtp_cur) amount1 = calc_amount1(liq, sqrtp_low, sqrtp_cur) (amount0, amount1) > (998976618347425408, 5000000000000000000000)如你所见,这些数字接近我们要提供的数量,但是 ETH 略小。
提示:使用
cast --from-wei AMOUNT将 wei 转换为 ether,例如:cast --from-wei 998976618347425280将输出0.998976618347425280。