Uniswap v3 定价系列1: 停时与鞅
- Antalpha Labs
- 发布于 2023-12-28 09:07
- 阅读 4529
作为一个uniswap v3 的流动性提供者,你的手续费能收多久?
本系列是第一次使用停时这一数学工具处理v3 lp 的定价。
这会是一个相对长的系列,旅程的终点是对uniswap v3 给出一个合理的定价公式。作为第一章,我们先讨论一个有趣的问题。作为一个uniswap v3 的流动性提供者,你的手续费能收多久?实际上这个问题非常棘手,也需要比较多的前置知识。整个系列需要对下面的知识有一些了解
-
布朗运动 和几何布朗运动
-
RN 导数
-
Laplace 变换
-
鞅和最优停时定理
本文还会假定你阅读过uniswap v3 白皮书。不要害怕,在读完全文后你会理解为什么需要这些数学工具,以及非常好的结论。当然数学是比较难的,非常推荐你通读全文后,对不熟悉的数学工具和部分在重新推导。
首次到达时间
对于firsting hitting time 最好的教程来自于 Shreve 的 Stochastic Calculus for Finance II 的3.6。对于一个布朗运动 $W_t$ ,First hitting time 可以定义为
$$ \tau_m = \min{t\ge 0;W_t = m} $$
而我们想处理一个更有趣的停时,我们会有两个边界(a,b),到达其中一个,布朗运动就会停止。
$$ \tau = \min{t\ge 0; W_t \not \in (a,b),a<0,b>0} $$
对于这个新的停时,我们想研究一些简单的性质。比如 $\tau$ 停在a 的概率是多少?我们会不加证明的使用下面的结论 如果一个过程是鞅,则其停时也是鞅。对于布朗运动,我们有下面三个鞅可以使用
-
$W_t$
-
$W_t^2-t$
-
$exp{\sigma W_t+\frac{1}{2}\sigma^2t }$
使用第一个鞅,我们可以得到
$$ W0= 0 = E(W\tau) = bP(W\tau=b)+aP(W\tau = a) $$
又因为
$$ P(W\tau=b)+P(W\tau=a)=1 $$
可以得到:
$$ P(W\tau=a) =\frac{b}{b-a}, P(W\tau=b) =\frac{-a}{b-a} $$
我们继续使用第二个鞅:使用第二个鞅
$$ 0 = E(w\tau^2-\tau)\ E[\tau] =a^2P(W\tau=a)+b^2P(W_\tau=b) = -ab $$
此时我们已经得知 $E[\tau]$ 的计算方法了。在进入更难的第三个鞅之前,我们先看看 $\tau$ 有什么用。
v3 简化例子
假设我是一个 v3 流动性提供者,当价格触达边界后,我会立刻停止提供流动性,撤回资金。我想知道我会收取多久的手续费。
我们需要对价格的运动做一个简单的假设,drift rate $\mu = 0$ : $d S = \sigma W_t $
价格 eth 价格 \$2000, 我的做市范围是(1500,2500),波动率为 50% yearly. 我们首先要先将做市范围和价格转换成布朗运动
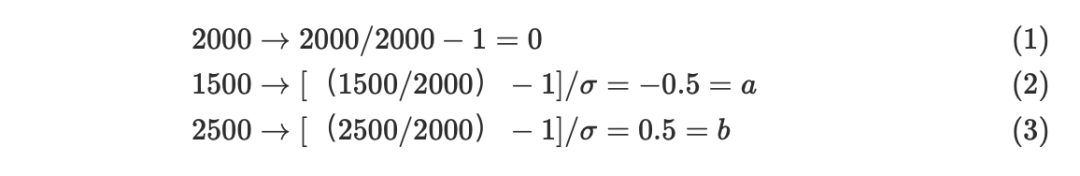
这样我们将问题转换成标准布朗运动下的停时问题。那我们的停时的期望为 $E[\tau] = -ab = 0.25$ 也就是预期我能收取手续费的时间长度为 0.25年。
期望
为了简化计算和方便理解,我们这里做一个不切实际的假设,无风险利率为0,在系列的后续文章我们会重新修改这一假设,讨论引入无风险利率后的模型变化。这意味着我们的pv = fv,没有贴现。此外我们还需要假定手续费的收取是在价格到达做市边界时就结束的,并不会实时收取并再投资。我们可以开启我们第一个简易定价模型了。
$$ E[V] = E[LP]+E[Fee] $$
lp
对于价值 \$1 的 lp,我们有任意时间 lp 价值的分段函数,此处我们做归一化
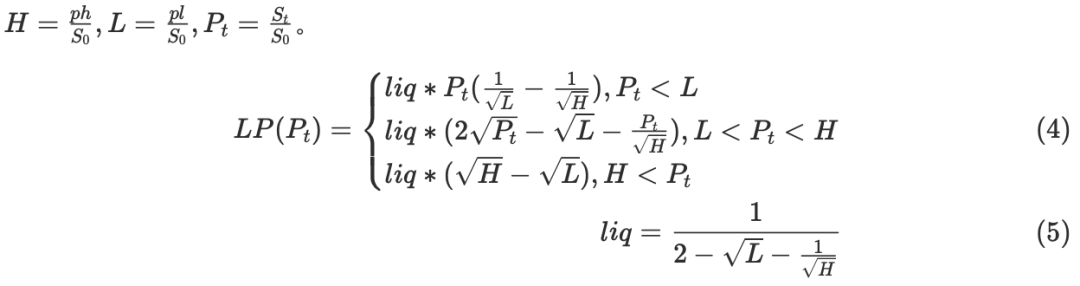
由于我们的策略要求我们持有到 $\tau$ ,所以 $P_t$ 只有L 和 H 两种可能。我们可以计算出我们的lp 价值为
$$ E[LP] = Prob(P\tau==H)*LP(H)+Prob(P\tau==L)*LP(L)\ $$
对于我们的例子来说,经过除以波动率,转化为

得到 lp 的期望为
$$ 0.5LP(H)+0.5LP(L) = 0.9334553114807631 $$
也就是 lp 是预期会亏损 7%。那么手续费能弥补回来嘛?
Fee
这部分其实也非常直观。 $fee = \tau*\phi$ ,其中 $\phi$ 为手续费收取速率。我们需要对 $\phi$ 手续费到达速率做一些扩展,我们增加假设:在任何价格上的流动性等同于当前的流动性,也就是流动性在任何价格上都一样。
那我们不难得出手续费的收入和我们提供的流动性正相关。也就是 $\phi(H,L) =\text{daily total fee} \cdot \frac{\text{liq}}{\text{generalized liq}}*365$
其中 total fee 是一个手续费到达的速率,我们再合理的展开为,由于我们波动率是年为单位的,所以要转换成365天。
我们以 https://info.uniswap.org/#/pools/0x88e6a0c2ddd26feeb64f039a2c41296fcb3f5640为例子,时间为2023年 12月25日。
其中24小时手续费为 \$113640,也可以根据成交量乘以池的手续费比例得到 ,在etherscan 查询得到流动性为 https://etherscan.io/address/0x88e6a0c2ddd26feeb64f039a2c41296fcb3f5640#readContract :
$\text{total liq}=21997540583974984595$
有关于fee 的相关推导参考附录。公式为
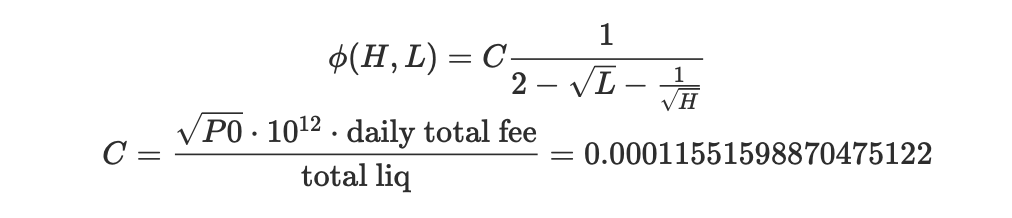
我们的预期手续费收入为
$$ E[\text{fee}] = C\cdot E[\tau] \cdot 365 \cdot \frac{1}{2-\sqrt{L}-\frac{1}{\sqrt{H}}} $$
带入相关的参数 手续费预期收入为 0.04400312313890215。
考虑到我们之前的LP 本身预期亏损 7%,手续费收入不足以覆盖成本。
object function
我们通过上面的推导得出以这个参数做市不成立。我们是否可以选取最佳的做市范围呢。我们只需要重新整理下公式,再使用一些简单的微积分即可。
入参:
-
年化波动率 $\sigma$
-
单位手续费速率 C,是一个统计值。 $C = \frac{\sqrt{P0}\cdot 10^{12}\cdot \text{daily total fee}}{\text{total liq}}$
-
归一化的做市范围 0< L < 1 < H<l<1<h$< section=""></l<1<h$<>
中间变量
-
布朗运动边界: $a = (L-1)/\sigma,b = (H-1)/\sigma$
-
停时期望 $E[\tau] = -ab =-\frac{(L-1)(H-1)}{\sigma^2} $
-
H,L处退出概率 分别为H: $\frac{b}{b-a}=\frac{H-1}{H-L},L:\frac{1-L}{H-L}$
-
归一化流动性 $liq =\frac{1}{2-\sqrt{L}-\frac{1}{\sqrt{H}}} $
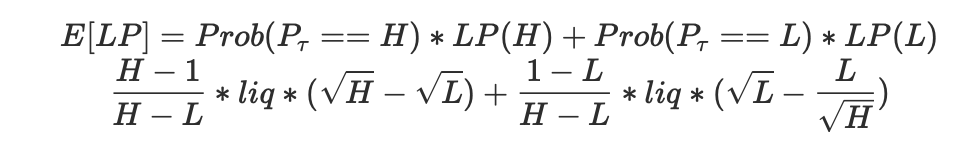
手续费:
$$ E[\text{fee}] = C\cdot E[\tau] \cdot 365 \cdot \frac{1}{2-\sqrt{L}-\frac{1}{\sqrt{H}}} $$
我们将两者相加,可以整理为
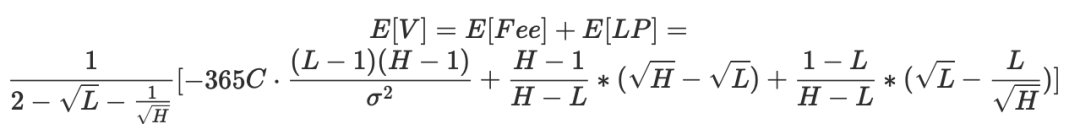
化简得到:
$$ E[V]= -\frac{(H-1) \left(\frac{1}{\sqrt{H}+\sqrt{L}}-\frac{365 C (L-1)}{\sigma ^2}\right)}{\frac{1}{\sqrt{H}}+\sqrt{L}-2} $$
我们是否要最大化 $E[V]$ 呢,并不是。一小时赚 $1要好于一天赚$ 10。因此我们的最优化目标函数为
$$ E[\frac{V-1}{\tau}] $$
如果 $E[\frac{V-1}{\tau}] = \frac{E[V] -1}{E[\tau]}$ 我们就将可以代入公式,进行求导选择最优的做市范围。旅程不总是一帆风顺的,这个等式是 「不成立」 的!原因是 jensen's 不等式,期望是不能交换顺序的 https://en.wikipedia.org/wiki/Jensen%27s_inequality 。那么我们可以直接求等式左边的期望嘛,当然可以! $\frac{V-1}{\tau}$ 中唯一的随机变量是 $\tau$ ,那么按照期望的计算公式,可得
$$ E[\frac{V-1}{\tau}] = \int_0^{\infty} \frac{V-1}{\tau}p(\tau) d\tau $$
在下一篇中,我们将使用第三个鞅来求出 $\tau$ 的分布。
附录 v3 lp math 推导
lp v3 的推导有大量优秀的文档可以参考,在本文中需要额外解决两个问题 1. 为了方便定价需要使得初始投资额为 \$1. 2. 需要将evm 的流动性转换成数学世界的流动性,这需要我们稍微回顾一下智能合约的计算。
我们增加了一个额外的条件 $P_0x+y = 1$ ,其中 x 是我们投入到流动性中的 eth 数量,y 是 usdc 数量。假定我们提供流动性是 $P_L<p_0<p_h$,我们可以通过流动性增加的规则和投资总额的约束,求出x,y 的值,进而得出 l="" 的值。<="" p="">
在白皮书中有如下的公式:
$$ (x_{real}+\frac{L}{\sqrt{pb}})(y{real}+L\sqrt{p_a}) = L^2 $$
在 https://atiselsts.github.io/pdfs/uniswap-v3-liquidity-math.pdf 中最后整理为 x, y, P, pa, pb 的关系为:
$$ x = L\frac{\sqrt{P_b}-\sqrt{P_c}}{\sqrt{P_c}\cdot \sqrt{P_b}} = L(\frac{1}{\sqrt{P_c}}-\frac{1}{\sqrt{P_b}})\ y = L(\sqrt{P_c}-\sqrt{P_a}) $$
将 x,y 带入到总投资 \$1中,作为初始投资,$ P_c = P_0$得到
$$ L(\frac{1}{\sqrt{P_0}}-\frac{1}{\sqrt{P_b}})\cdot P_0 + L(\sqrt{P_0}-\sqrt{P_a}) = 1 $$
得到 $L =\frac{1}{2\sqrt{P_0}-\frac{P_0}{\sqrt{p_b}}-\sqrt{P_a}} $ , 我们进一步将其归一化, $H= \frac{ph}{S_0},L = \frac{pl}{S_0},P_t = \frac{S_t}{S_0}$ 。得到我们的 $liq=\frac{1}{2-\sqrt{L}-\frac{1}{\sqrt{H}}} $ 从而计算出后续出 $V_t$ 的函数。
对于我们来说有如下的关系

对于在智能合约中得到的当前流动性数据我们如何将其转换回generlized world是我们接下来要讨论的问题,如果能转换回来,我们将能方便的处理好手续费分成问题,进而能方便的开展求导等后续最优化问题。
参考 https://uniswapv3book.com/milestone_1/calculating-liquidity.html ,和其中的相关代码,我们可以做出如下推理
evm world 中的 $L_{vm}$ 由于solidity的限制 和gas 优化,有一些改动,比如价格的格式也和现实中不一样。但是两者的公式是一致的,比如
$$ L = \Delta x \frac{\sqrt{P_b}\sqrt{P_c}}{\sqrt{P_b}-\sqrt{P_c}} $$
对于evm 中,我们需要做一些代换,现实中的价格是有 decimal,需要转换成 evm 中无单位价格,其中 usdc,usdt,eth 的decimal 分别为 6,18,18.

那么我就可以方便的计算出 generlized 公式下的的手续费分成了。我们需要将从智能合约的 $L{vm}$ 转换成真实世界的L, 再乘以 $\sqrt{P0}$ 转换成generlized 的 流动性 $L{gen}$ ,此时我们可以直接将 $liq = \frac{1}{2-\sqrt{L}-\frac{1}{\sqrt{H}}}$ 除以我们转换后的总流动性 $L_{gen}$ ,即我们提供的$1 的流动性占比。
ref
-
Shreve, S.E. (2004) Stochastic Calculus for Finance II Continuous-Time Models. Springer, Berlin.
-
about Jensen inequality https://en.wikipedia.org/wiki/Jensen%27s_inequality
Antalpha Labs 是一个非盈利的Web3开发者社区,致力于通过发起和支持开源软件推动Web3技术的创新和应用。
官网: https://labs.antalpha.com
Twitter: https://twitter.com/Antalpha_Labs
Youtube: https://www.youtube.com/channel/UCNFowsoGM9OI2NcEP2EFgrw
联系我们: hello.labs@antalpha.com
- 转载
- 学分: 25
- 分类: DeFi
- 标签: Uniswap V3 DeFi
- Uniswap v3 白皮书与代码解析 49 浏览
- 我让Claude拥有了AAVE的“眼睛”:结果如何 129 浏览
- MetaDAO 2025年第四季度季度报告 179 浏览
- Orca Whirlpools 对比 Uniswap V3 — ImmuneBytes 171 浏览
- 流动性战争与对抗性代币激励策略——ImmuneBytes 192 浏览
- DeFi中的跨链桥最佳实践是什么?- CoW DAO 213 浏览
- Pendle 发布 2026年战略展望 276 浏览
- 2026 年智能合约审计的实际成本 286 浏览
- Zyfai - 一个代理收益层 261 浏览
- MiCA与DeFi:去中心化协议需知事项 324 浏览
- DeFi领域DYOR:一份综合指南 - CoW DAO 283 浏览
- DeFi 介绍 - CoW DAO 344 浏览

