简述零知识证明与zkSNARK
- 元家昕
- 发布于 2019-04-16 15:10
- 阅读 16218
今天这篇文章我们一起来看一下zkSNARK这个拗口的技术到底是什么鬼。
今天这篇文章我们一起来看一下zkSNARK这个拗口的技术到底是什么鬼。
什么是零知识证明
要了解zkSNARK,必须先理解什么是零知识证明。
关于零知识证明,概念并不难理解,我们以一个老掉牙的故事作为例子。
阿里巴巴被强盗抓住,为了保命,他需要向强盗证明自己拥有打开石门的密码,同时又不能把密码告诉强盗。他想出一个解决办法,先让强盗离开自己一箭之地,距离足够远让强盗无法听到口令,足够近让阿里巴巴无法在强盗的弓箭下逃生。阿里巴巴就在这个距离下向强盗展示了石门的打开和关闭。
这个整个过程就是零知识证明,证明者能够在不向验证者提供任何有用信息(石门的口令)的情况下,使验证者相信某个论断(阿里巴巴知道打开石门的方法)是正确的。
当然,现实生活中类似的应用有很多,大家可以参考阿里巴巴的零知识证明或者零知识证明。
在计算机世界里面,零知识的应用场景就更多了,例如我们常用非对称加密来做身份认证,验证方只要使用公钥解出自己提供的随机数,即可证明被认证方的身份,不需要其提供自己的私钥。
以上例子都是针对特定场景的特定方法,比如说石门不是通过口令控制而是通过实物钥匙控制,这个方法就不可用了,是否有一个通用方法去认证任何事件呢?
什么是zkSNARK
zkSNARK是zero-knowledge succint non-interactive arguments of knowledge的简称,全称里面每个单词都有特定的含义:
- Zero knowledge:零知识证明,见前文。
- Succinctness:证据信息较短,方便验证。
- Non-interactivity:几乎没有交互,证明者基本上只要提供一个字符串义工验证。对于区块链来说,这一点至关重要,意味着可以把该消息放在链上公开验证。
- Arguments:证明过程是计算完好(computationally soundness)的,证明者无法在合理的时间内造出伪证(破解)。跟计算完好对应的是理论完好(perfect soundness),密码学里面一般都是要求计算完好。
- of knowledge:对于一个证明者来说,在不知晓特定证明 (witness) 的前提下,构建一个有效的零知识证据是不可能的。
接下来,我们一步一步解释这个zkSNARK到底是怎么实现的。
同态隐藏
说到zkSNARK,不能不提的一个概念就是同态隐藏,说它是zkSNARK的核心技术一点都不为过。
满足下面三个条件的函数E(x),我们称之为加法同态。
- 对于大部分的x,在给定的E(x)通常很难求解出x.
- 不同输入将会得到不同输出 - 因此如果x≠y,,则E(x)≠E(y).
- 如果某人知道了E(x)和E(y),,则他可以生成在算数运算式中的x和y.。比如,他们可以使用E(x)和E(y).来计算E(x+y)。
同理我们可以定义乘法同态甚至是全同态。
我们常用的的非对称加密方式RSA和ECC都支持加法同态,计算和证明证明需要比较多的公式运算,有时间另外开一篇文章讲解。
编者注:上面也许上作者笔误,有同学指出: RSA 是典型的乘同态,Paillier 才是加同态。 跟RSA和ECC(椭圆加密算法)一样,注意这里的E(x)计算是在有限域里面进行,这个域下文称为Fp。
有了同态隐藏这个利器以后,我们就可以实现一定程度的零知识证明了。
A拥有x和y两个秘密的数字,需要向B证明这两个数字的和是7,只需要执行下面三个步骤:
- A计算E(x),E(y),并发送给B
- 因为函数E(x)满足加法同态,B可以通过E(x),E(y)计算E(x+y)
- B独立计算E(7),并验证E(x+y)=E(7)
多项式盲验证
利用加法同态的特性,我们可以简单的把零知识证明推广到多项式中。
假定A知道一个最高d次的多项式P,而B想要知道对应某个s的E(P(s))
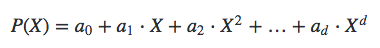
我们希望在验证的过程中,A只知道P,不知道s,B只知道s,不知道P,可以通过下面方式实现:
- 对s的每个指数,B计算E(1),E(s),...,E(sd),并发送给A
- A知道多项式的所有系数,可以利用同态特性计算P(s),并回送给B
KCA以及完整的多项式盲验证
上面提供的多项式盲验证方式有一个致命的问题,就是B根本没法验证A是真正利用多项式P(s)去计算结果,也就是说无法证明A真正知道这个多项式P(X)。我们继续完善一下上面的验证。
我们先定义一个概念:α对是指满足b=α*a的一对值(a,b)。注意这里的乘法其实是椭圆曲线(ECC)上的乘法,椭圆曲线上的运算符合两个特性:
- 是当α值很大的情况下,很难通过a和b倒推出α;
- 是加法和乘法满足可交换群的特性,也就是说加法和乘法交换律在椭圆曲线上也是成立的。椭圆曲线的运算较复杂,本文暂不详述,大家只要记住椭圆函数的乘法满足同态隐藏的特性,即可完成下面的证明。
我们利用α对的特性,构建一个称为KCA(Knowledge of Coefficient Test and Assumption)的过程:
- B随机选择一个α生成α对(a,b),α自己保存,(a,b)发送给A
- A选择γ,生成(a′,b′)=(γ⋅a,γ⋅b),把(a′,b′)回传给B。利用交换律,可以证明(a′,b′)也是一个α对,b′=γ⋅b=γα⋅a=α(γ⋅a)=α⋅a′
- B校验(a′,b′),证实是α对,就可以断言A知道γ
这个证明可以推广到多个α对的场景,称为d-KCA
- B发送一系列的α对给A
- A使用(a′,b′)=(c1⋅a1+c2⋅a2,c1⋅b1+c2⋅b2)生成新的α对
- B验证通过,可以断言A知道c数组
这个KCA咋看似乎没有什么用,但正好可以补足了之前多项式盲验证 的缺陷,一个完整的多项式盲验证过程如下:
- 因为椭圆曲线的乘法符合同态隐藏的特性,A和B可以共同选择x⋅g作为E(x)
- B计算g,s⋅g,…,sd⋅g和α⋅g,αs⋅g,…,αsd⋅g并发送给A,实际上过程同上一章的第一步,只是把E(x)替代成乘法,增加了αs相应的多项式结果
- A计算a=P(s)⋅g,b=αP(s)⋅g并回传
- a值即为B所需校验的E(P(s))结果,同时KCA保证了a值必然是通过多项式生成
好了,到这里喘口气,回顾一下我们现在到底做到了些什么。
通过加法同态,我们可以实现加法隐藏,让B在不知道x和y的情况下,校验x+y的值。进一步,通过多项式盲验证,我们可以在不暴露多项式P(X)的情况下,让B校验任意给定s对应的P(s)。
接下来坐好扶稳,我们要从多项式推广到任意计算的盲验证了。
任意计算转换到多项式证明
直接上例子,假定A需要向B证明他知道c1,c2,c3,使(c1⋅c2)⋅(c1+c3)=7,按照惯例,c1,c2,c3需要对B保密。
我们要做的第一步就是把计算“拍平”,通过基本的运算符把原计算画成这样的“计算门电路”。
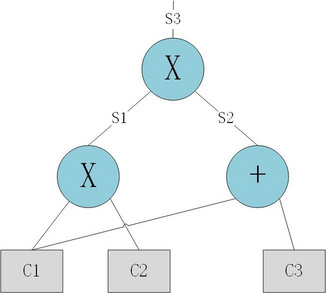
当然我们也可以用程序员比较熟悉的方式来表达
S1=C1C2 S2=C1+C3 S3=S1S2
通过增加中间变量,我们把复杂的计算拍平,使用最简单的门电路表达。新的门电路跟原计算是等价的。我们要做的第二步就是把每一个门电路表示为等价的向量点积形式,这个过程成为R1CS(rank-1 constraint system)。对每个门电路,我们定义一组向量(a,b,c),使得s . a * s . b - s . c = 0。其中s代表全部输入的向量,也就是[C1,C2,C3,S1,S2,S3],为了让加法门也能用同样的方式表达,我们增加一个虚拟的变量成为one,s向量变成[one,C1,C2,C3,S1,S2,S3]。对应到第一个门
a=[0,1,0,0,0,0,0] b=[0,0,1,0,0,0,0] c=[0,0,0,0,1,0,0]
把s,a,b和c代入s . a s . b - s . c = 0,得到C1C2-S1=0,即这个向量表达跟第一个门是完全等价的。
同理我们可以计算第二个门
a=[1,0,0,0,0,0,0] b=[0,1,0,1,0,0,0] c=[0,0,0,0,0,1,0]
第三个门
a=[0,0,0,0,1,0,0] b=[0,0,0,0,0,1,0] c=[0,0,0,0,0,0,1]
好了,到这里,我们把一个计算式拍平成为门电路,接着又通过R1CS把门电路“编码”成向量的表达方式。接下来是最重要的一步,把向量表达式表示为多项式,从而把向量的验证转化为多项式的验证,这个过程称为QAP(Quadratic Arithmetic Programs) 具体办法是,在Fp上面选定任意三个不同的值,例如我们选定1,2,3,寻找一组多项式
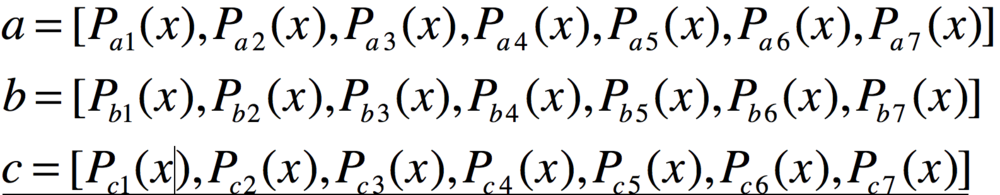
使得多项式在x取值1,2,3的时候a,b,c数组的取值分别对应到前述三个门电路的向量。
问题转化为通过已知解倒推多项式定义,这部分可以使用拉格朗日插值完成,本文不再详述。这个过程中需要对向量的每个取值做拉格朗日插值,对于复杂问题,这个向量会非常庞大,计算过程会很复杂,这里可以利用快速傅里叶变换进行优化。
到这里,我们把原来的三个向量组表示成为一个用x表示的数组a(x),b(x),c(x)。
取多项式P(x)=s . a(x) s . b(x) - s . c(x),根据我们原来的定义,在x取值为1,2或3的时候,P(x)=0。根据多项式特性,P(a)=0等价于P可以被(x-a)整除,P(x)一定能被(x-1)(x-2)(x-3)整除,也就是说存在H(X),使P(x)=T(x)H(x),其中T(x)=(x-1)(x-2)(x-3)。
注意QAP这个过程把原来三个点的取值转化成为一个多项式,相当于中间插入了很多没有意义的值,这些值的取值与原公式是无关的。也就是说多项式的验证与原计算的验证本质并不等价,但验证了多项式也就验证了元计算。
好了,最终我们把原算式的证明转化成为多项式的证明,只要证明P(x)=T(x)*H(x),即可验证原算式。
匹诺曹协议
通过QAP,我们已经把计算式的证明转化为多项式的证明,现在万事具备,只欠东风,就差一个完整的验证流程了。
为了简化下文描述,我们定义s . a(x)为L(x),s . b(x)为R(x),s . c(x)为O(x),那么我们需要证明的等式就改写成L(x)R(x)-O(x)=T(x)H(x)。L,R和O的最高阶数是d,所以这个等式的最高阶数是2d,我们知道,两个不等价的多项式交点数量最多只有2d个,2d相较于有限域的元素个数p来说很小的情况下,我们可以采用采样的方式验证多项式相等,A随意选择多项式P(x)被校验通过的概率只有2d/p。随机采样校验的过程如下:
- A按照上一章方法选择多项式L,R,O,H
- B选择随机点s,计算E(T(s))
- A计算E(L(s)),E(R(s)),E(O(s)),E(H(s)) (根据B发过来的E(s),E(s2),...)
- B检验E(L(s)R(s)-O(s))=E(H(s)T(s))
这个证明过程还有四个问题需要解决:
1. 保证L,R,O从同一组参数s生成
这个证明过程存在一个缺陷,正如按照我们的定义L(x)=s . a(x),R(x)=s . b(x),O(x)=s . c(x),这里隐含了一个限定条件是L,R和O必须是由同一个向量s生成,证明中忽略了这一点,也就是说A可以通过选择不符合这个限定条件的多项式来作弊。解决办法仍然是KCA,只不过这次的KCA要复杂一些。 先定义两个公式:
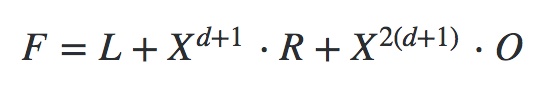
这个公式的含义是要把L,R,O的指数错开,如果L,R,O真是从同一组s=[s1,....sm]生成的话,必然有
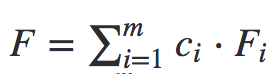
换句话说,只要A能给出F和Fi的线性组合,即可证明L,R,O符合限定条件。这个限定条件的问题就转化为一个d-KCA的问题了。
1.B选择隐秘的α,计算E(α*Fi)并发送给A
2.A计算E(αF)回传给B
3.B根据本文公式自行计算E(F)并校验α对2. 防止暴力破解
在现在的流程里面,A需要把E(L(s)),E(R(s)),E(O(s)),根据同态隐藏的特性,根据这些值无法倒推原多项式。但是如果需要验证的问题,解不多的情况下,B还是可以通过穷举的方式暴力破解原问题,得到A的原始数据。例如我们已知A有两个正整数,要求盲验证这两个正整数的乘积是12,那么B完全可以穷举乘积是12的所有正整数组合,正向执行验证过程,与E(L(s)),E(R(s))和E(O(s))比对即可知道正确的答案是什么。 当然,我们也有解决办法。解决思路就是在生成L,R,O的时候引入随机偏置
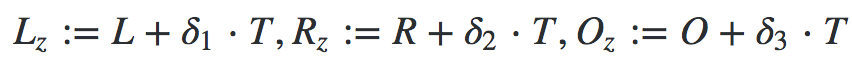
因为:
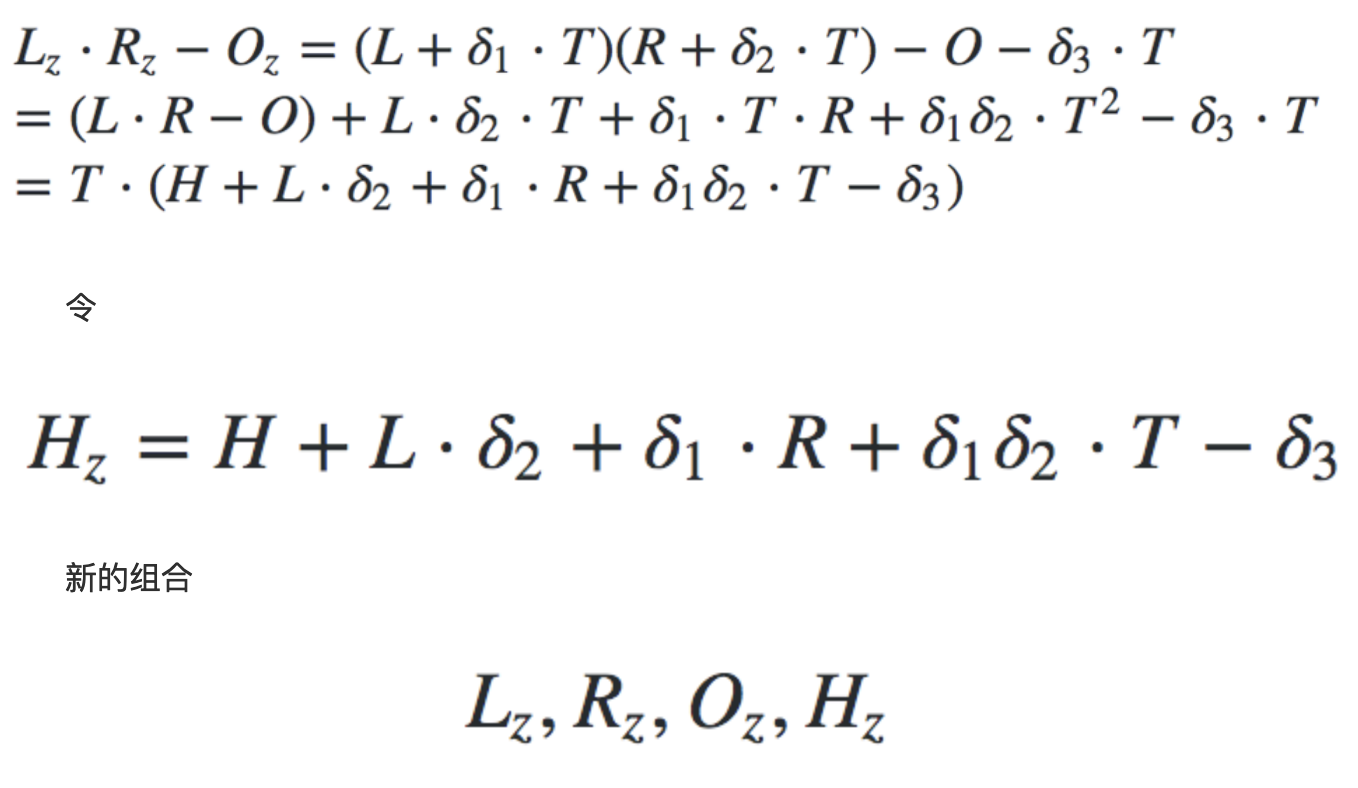
任然可以通过多项式的校验,而因为B不知道随机数,也无法通过暴力破解的方式知晓原始参数。
3. 乘法同态
匹诺曹协议的最后一步,B需要检验E(L(s)R(s)-O(s))=E(H(s)T(s)),而事实上,我们之前只提到E(x)满足加法同态,B是无法通过E(H(s))计算出E(H(s)*T(s))的。 解决办法需要回归到我们的数学工具上,我们需要用到椭圆曲线配对的特性,这里说来话长,本文只给出结论。通过椭圆曲线配对,我们可以得到一个弱化版的乘法同态。 定义E1(x):=x⋅g,E2(x):=x⋅h,E(x):=x⋅g,因为三个函数都是椭圆曲线,自然分别都符合加法同态,同时椭圆曲线配对特性可以保证我们能通过E1(x),E2(y)计算E(xy)。
4. 减少交互
最后一个问题也是最关键的一个问题是,匹诺曹协议中需要A和B之间做很多的消息交互,而在区块链中,我们想要做到的是“公开认证”。最理想的情况就是只要A把证据作为一个字符串放置到链上,任何人都能验证结论。 可惜的是,实际上这种严格意义上的零交互证明已经被证明不能满足所有的证明场景。我们退而求其次,采用了一种称为CRS(COMMON REFERENCE STRING)的方式。原理很简单,实际上就是把随机数α和s内置于“系统”中。 所以终极版的zkSNARK过程就是:
0.配置α和s,以之计算 (E1(1),E1(s),…,E1(sd),E2(α),E2(αs),…,E2(αsd))E2(α),并公示 1.A使用公示参数计算验证多项式 2.B校验多项式,乘法同态部分利用椭圆曲线配对的特性完成,形如E(αx)=Tate(E1(x),E2(α))
当然CRS有一个极其严重的问题就是,“系统”内建的随机参数非常重要,知道这个秘密参数的人就拥有超级管理员的权限,可以任意制造伪币,这在一个去中心化的系统中几乎是不可接受的。 事实上,ZCash的系统参数采用了一种影视剧中经常出现的桥段去“保护”这个不应该也不需要由任何人掌握的配置数据。选择世界各地六个可信任的人,每人生成密钥一部分,六个人的密码拼接在一起生成公示的数据后,再分别销毁掉各自手上的密钥。除非六人合谋作弊,否则没有人拥有超级管理员的权限。 。
参考文献
- ZCash 7篇文章,有社区翻译版,但还是推荐看原汁原味的snark-explain
- Vitalik 3篇文章,小天才作者我就不介绍了,这三篇介绍得也是很透彻, [1], [2], [3]
- 零知识证明 - zkSNARK 入门
- libsnark开源库地址
本文作者元家昕, 深入浅出经授权区块链转载,为更好的阅读效果对原文 略有修改。
- ZK编年史:哈希登场 118 浏览
- 以太坊协议研究学习小组 - 2026 启动 224 浏览
- 神奇的 Zig、C 和 OpenSSL 184 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 331 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 277 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 354 浏览
- Shamir份额的魔力:BLS门限签名 463 浏览
- Zcash:比特币遗忘的隐私 429 浏览
- ZK编年史:计算模型 296 浏览
- lambdaworks 2026 年更新路线图和优先级 360 浏览
- 2026年构建机构级DeFi平台真正需要什么 894 浏览
- zkMesh:2026年1月回顾 447 浏览

