zkMIPS解读
【zkMIPS系列】ZKM Prover生成一个证明与聚合
- ZKM
- 发布于 2024-12-19 16:33
- 阅读 2191
ZKM Prover利用Plonky2构造零知识证明系统,其主要步骤涉及对每个Plonkish表的证明生成、聚合及压缩处理。
1. ZKM Prover证明架构
ZKM Prover利用Plonky2构造零知识证明系统,其主要步骤涉及对每个Plonkish表的证明生成、聚合及压缩处理。具体过程如下:
1.1 对每个Plonkish表生成Plonky2证明
在该步骤中,对于每个Plonkish表,ZKM Prover会通过Plonky2算法生成一组证明。这些证明包括Permutation Check、lookup argument等多个子证明。这些子证明确保了Plonkish表中的各项数据在满足给定约束条件的同时,保持了数据的隐私性和有效性。具体的证明结构可以根据需要进行扩展和定制。例如,Permutation Check可以证明输入值之间的排列关系,而lookup argument则验证表格查找操作的正确性。这些证明将确保数据在验证过程中能够通过零知识证明验证其合法性,但不泄露任何其他信息,如图1所示。
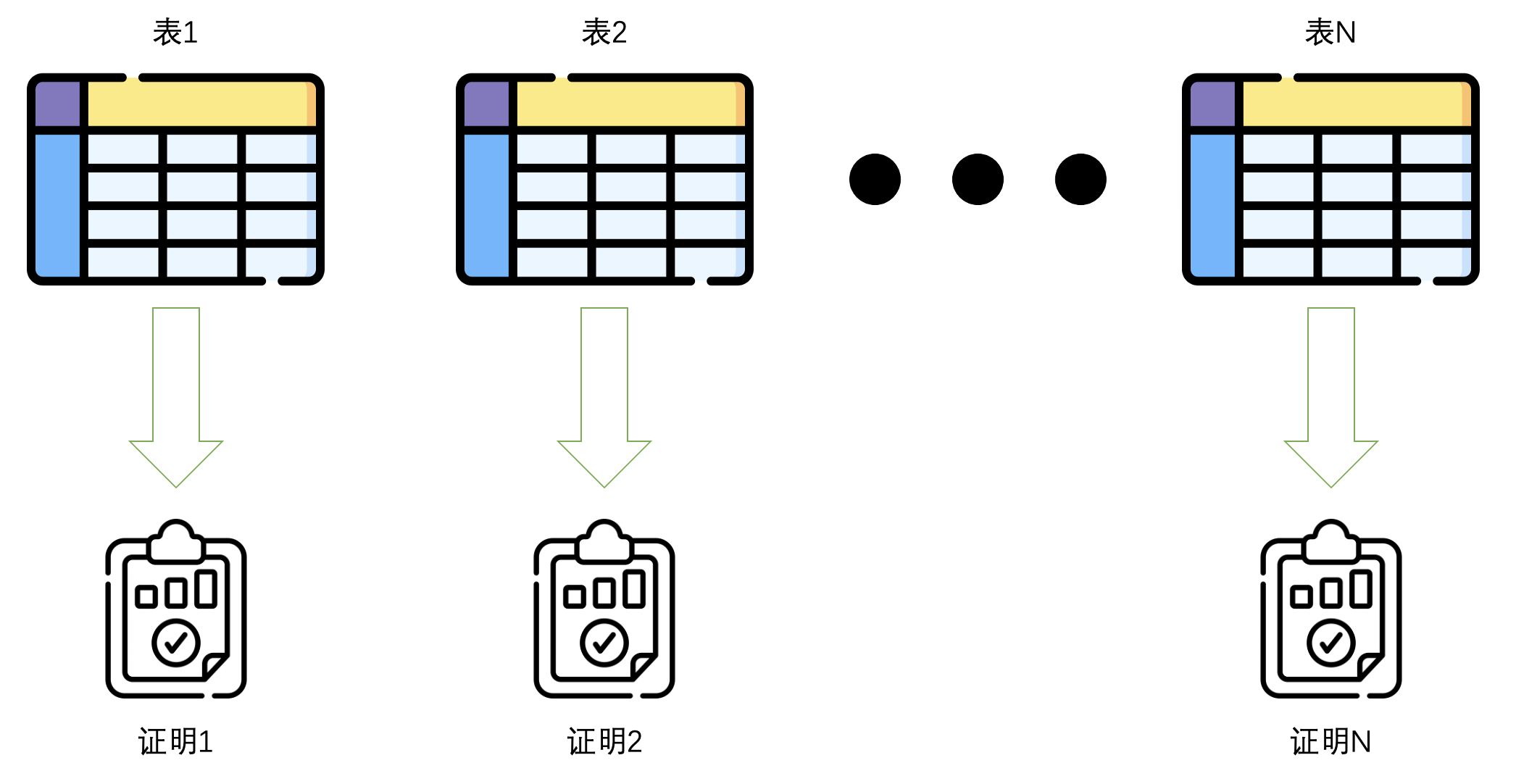 图1. 每个Plonkish表对应一个证明
图1. 每个Plonkish表对应一个证明
1.2 聚合Plonkish表生成的Plonky2证明
在生成了每个Plonkish表的Plonky2证明后,ZKM Prover需要将这些证明合并成一个整体的Root Proof。具体来说,首先将每个Plonkish表生成的Plonky2证明描述为一个电路,即将其转化为一个逻辑电路形式的验证问题。在这个电路中,输入是各个Plonkish表的生成证明,输出是经过验证的整体证明。接下来,Plonky2算法被再次调用,对每个独立的Plonkish证明进行聚合,得到一个统一的Root Proof。这个Root Proof是多个证明的合成,它保证了所有独立证明的正确性,并且可以通过一个单一的证明来验证多个Plonkish表的有效性,如图2所示。聚合的方式通常涉及多个子证明的随机线性组合(random linear combination),从而将多个约束信息压缩为一个单一的Root Proof。
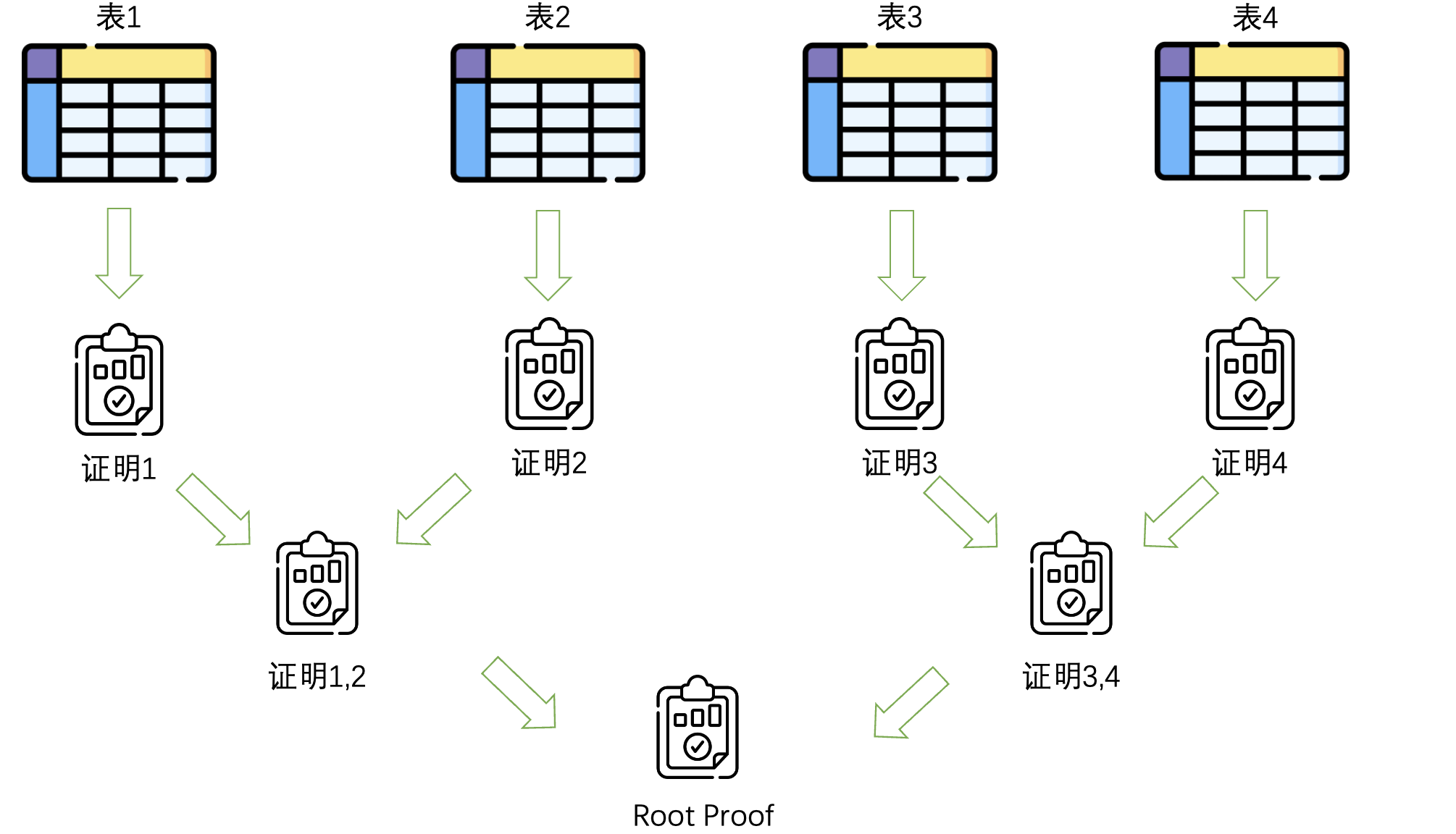 图2. 所有的Plonkish证明聚合为一个证明
图2. 所有的Plonkish证明聚合为一个证明
1.3 Root Proof的压缩并转换为SNARK Proof
由于Root Proof是一个STARK Proof,其长度可能较长,因此在进行验证时会带来较大的开销。因此,ZKM Prover需要对STARK Proof进行压缩,以减少验证所需的计算量和存储空间。在此过程中,Root Proof首先被描述为一个电路,该电路通过检验Root Proof的有效性来进行验证。接着,ZKM Prover会利用现有的zkSNARK算法,如Groth16或Plonk,进一步压缩STARK Proof并将其转换为SNARK Proof。Groth16和Plonk算法作为成熟的zkSNARK技术,能够在保证零知识性的同时,显著提高证明的验证效率。通过这一转换,ZKM Prover能够将较长的STARK Proof转换为较短的SNARK Proof,从而有效地降低验证成本并提高系统的吞吐量。
2. zkVM证明流程
本系列将首先介绍zkVM中每个组件(对应每个Plonkish的表)对应证明的生成方式,包括以下模块,代码如下:
pub struct AllStark<F: RichField + Extendable<D>, const D: usize> {
pub arithmetic_stark: ArithmeticStark<F, D>,
pub cpu_stark: CpuStark<F, D>,
pub poseidon_stark: PoseidonStark<F, D>,
pub poseidon_sponge_stark: PoseidonSpongeStark<F, D>,
pub logic_stark: LogicStark<F, D>,
pub memory_stark: MemoryStark<F, D>,
pub cross_table_lookups: Vec<CrossTableLookup<F>>,
}
// prover/src/all_stark.rs接下来介绍每个模块的基本功能:
arithmetic_stark:验证算术运算的正确性,包括加法、乘法等基本操作。它确保计算过程符合预期的算术规则,例如多项式计算、数值运算的合法性,并在电路中添加对应的约束。
cpu_stark:处理 CPU 指令仿真和逻辑执行的验证,确保指令序列的执行状态是正确的。这个模块模拟 CPU 执行环境,可以验证状态转换、寄存器更新和指令的执行顺序。
poseidon_stark:验证 Poseidon 哈希函数的计算过程,确保输入数据对应正确的哈希输出。Poseidon 是零知识友好的哈希函数,常用于 Merkle 树根的生成、哈希映射等密码学操作。
poseidon_sponge_stark:负责验证 Poseidon Sponge 构造的计算,确保哈希链或加密操作的正确性。Sponge 构造是一种通用框架,广泛用于随机数生成和哈希数据压缩等场景。
logic_stark:验证逻辑运算的正确性,包括布尔运算和位运算,例如 AND、OR 和 XOR 操作。这个模块用于约束电路中的逻辑推理,确保逻辑计算的结果与输入一致。
memory_stark:验证内存读写和状态管理的正确性,确保数据存储、加载和索引访问都符合预期。这个模块适用于验证程序执行过程中的内存一致性和状态变更。
cross_table_lookups:负责跨表查找的约束,将不同模块的计算结果连接起来,验证它们之间的数据依赖关系。它确保表格之间的输出与输入一致,实现跨模块的数据完整性和正确性。
证明聚合方法 (Proof Aggregation )
接下来,将从代码的角度重点介绍一下aggregation的方法:
- 段文件读取与内核生成:逐一加载段文件,生成对应的内核数据。
- 根证明生成:每个段生成独立的根证明。
- 递归聚合:通过
prove_aggregation将多个段的证明合并为一个综合证明。 - 区块证明生成:完成所有段处理后,生成最终区块证明。
- 验证:每个阶段均包含验证步骤,确保过程正确性。
代码相对路径为:prover/examples/zkmips.rs
2.1 初始化基础配置
本流程主要确定证明的环境、参数和依赖项,为后续操作打好基础,具体包括:
- 定义参数:
- 使用
GoldilocksField作为域,确保数学计算在特定有限域上完成。 - 配置
PoseidonGoldilocksConfig以支持 Poseidon 哈希。 - 使用递归参数
InnerParameters和OuterParameters,可能与 Groth16 zkSNARK 配置相关。
- 使用
- 输入检查:
- 确保段文件数量大于等于 2,一个文件对应一个电路;否则终止程序。
type InnerParameters = DefaultParameters;
type OuterParameters = Groth16WrapperParameters;
type F = GoldilocksField;
const D: usize = 2;
type C = PoseidonGoldilocksConfig;
if seg_file_number < 2 {
panic!("seg file number must >= 2\n");
}2.2 初始化电路与计时器
本流程主要初始化递归证明电路和时间跟踪器,具体包括:
- 初始化计时器:
TimingTree用于跟踪整个过程的耗时,方便性能优化。 - 创建 AllStark 对象:这是核心的证明结构,封装了多段证明的逻辑。
- 加载递归电路:
AllRecursiveCircuits提供递归电路的支持,确保后续证明可以进行递归合并。
let total_timing = TimingTree::new("prove total time", log::Level::Info);
let all_stark = AllStark::<F, D>::default();
let config = StarkConfig::standard_fast_config();
let all_circuits = AllRecursiveCircuits::<F, C, D>::new(&all_stark, &DEGREE_BITS_RANGE, &config);2.3 加载第一个段文件
读取第一个段文件并生成根证明,具体包括:
- 加载文件:通过路径读取第一个段文件。
- 生成内核数据:调用
segment_kernel解析段数据并生成初始输入。 - 生成根证明:调用
prove_root对第一个段进行证明,返回初始的聚合证明 (agg_proof) 和公共值。
let seg_file = format!("{}/{}", seg_dir, seg_start_id);
log::info!("Process segment {}", seg_file);
let seg_reader = BufReader::new(File::open(seg_file)?);
let input_first = segment_kernel(basedir, block, file, seg_reader, seg_size);
let mut timing = TimingTree::new("prove root first", log::Level::Info);
let (mut agg_proof, mut updated_agg_public_values) =
all_circuits.prove_root(&all_stark, &input_first, &config, &mut timing)?;2.4 验证根证明
验证生成的根证明是否正确,具体包括:
- 打印时间:输出根证明生成过程的耗时。
- 验证证明:调用
verify_root确保根证明的有效性。如果验证失败,程序会报错。
timing.filter(Duration::from_millis(100)).print();
all_circuits.verify_root(agg_proof.clone())?;2.5 加载第二个段文件并生成根证明
如果段文件数量为偶数,则处理第二个段并生成证明,具体包括:
- 读取第二个段文件:通过路径加载文件。
- 生成内核数据:调用
segment_kernel处理文件数据。 - 生成根证明:调用
prove_root对第二段生成证明。 - 验证根证明:通过
verify_root验证生成的根证明。
let seg_file = format!("{}/{}", seg_dir, seg_start_id + 1);
log::info!("Process segment {}", seg_file);
let seg_reader = BufReader::new(File::open(seg_file)?);
let input = segment_kernel(basedir, block, file, seg_reader, seg_size);
timing = TimingTree::new("prove root second", log::Level::Info);
let (root_proof, public_values) = all_circuits.prove_root(&all_stark, &input, &config, &mut timing)?;
timing.filter(Duration::from_millis(100)).print();
all_circuits.verify_root(root_proof.clone())?;2.6 合并两个段的证明
将前两个段的证明合并,更新公共值,具体包括:
- 更新公共值:合并两个段的公共值(
roots_before,roots_after和用户数据)。 - 合并证明:调用
prove_aggregation合并前两个根证明。 - 验证聚合证明:通过
verify_aggregation确保合并后的证明正确。
let agg_public_values = PublicValues {
roots_before: updated_agg_public_values.roots_before,
roots_after: public_values.roots_after,
userdata: public_values.userdata,
};
(agg_proof, updated_agg_public_values) = all_circuits.prove_aggregation(
false,
&agg_proof,
false,
&root_proof,
agg_public_values.clone(),
)?;
all_circuits.verify_aggregation(&agg_proof)?;
2.7 处理剩余的段文件
对每对段文件生成根证明并递归合并,具体包括:
- 加载每对段文件:读取偶数段和奇数段文件。
- 生成根证明:对两个段分别调用
prove_root生成证明。 - 递归合并:调用
prove_aggregation合并两个根证明。
for i in 0..seg_num / 2 {
let seg_file = format!("{}/{}", seg_dir, base_seg + (i << 1));
let seg_reader = BufReader::new(File::open(&seg_file)?);
let input_first = segment_kernel(basedir, block, file, seg_reader, seg_size);
let (root_proof_first, first_public_values) =
all_circuits.prove_root(&all_stark, &input_first, &config, &mut timing)?;
let seg_file = format!("{}/{}", seg_dir, base_seg + (i << 1) + 1);
let seg_reader = BufReader::new(File::open(&seg_file)?);
let input = segment_kernel(basedir, block, file, seg_reader, seg_size);
let (root_proof, public_values) =
all_circuits.prove_root(&all_stark, &input, &config, &mut timing)?;
let new_agg_public_values = PublicValues {
roots_before: first_public_values.roots_before,
roots_after: public_values.roots_after,
userdata: public_values.userdata,
};
let (new_agg_proof, new_updated_agg_public_values) = all_circuits.prove_aggregation(
false,
&root_proof_first,
false,
&root_proof,
new_agg_public_values,
)?;
}2.8 生成最终区块证明
完成所有段的递归聚合后,生成最终的区块证明,具体包括
- 调用
prove_block:生成最终的区块证明。 - 验证区块证明:调用
verify_block确保最终证明有效。
let (block_proof, _block_public_values) =
all_circuits.prove_block(None, &agg_proof, updated_agg_public_values)?;
all_circuits.verify_block(&block_proof)?;3. 调用函数解析
其中最关键的两大方法是prove_aggregation和prove_root,分别用于聚合证明和生成根证明:
一. 函数 prove_aggregation
这个函数的核心功能是执行 证明的递归聚合,通过将两个证明合并,生成一个新的聚合证明,同时维护公共值的正确性,其将两个证明 (lhs_proof 和 rhs_proof) 聚合为一个新的证明,并同时处理公共值 (public_values) 的更新,其主要步骤包括
- 电路绑定:将证明、公共值和验证数据映射到电路目标中。
- 证明生成:调用
prove方法在给定输入下生成聚合证明。 - 错误处理:使用
anyhow处理可能的公共值设置错误,增强鲁棒性。
代码相对路径为:prover/src/fixed_recursive_verifier.rs
函数定义
pub fn prove_aggregation(
&self,
lhs_is_agg: bool, // 左侧证明是否为聚合证明
lhs_proof: &ProofWithPublicInputs<F, C, D>, // 左侧证明(含公共输入)
rhs_is_agg: bool, // 右侧证明是否为聚合证明
rhs_proof: &ProofWithPublicInputs<F, C, D>, // 右侧证明(含公共输入)
public_values: PublicValues, // 公共值
) -> anyhow::Result<(ProofWithPublicInputs<F, C, D>, PublicValues)>输入参数:
lhs_is_agg和rhs_is_agg:分别指示左、右证明是否是聚合后的证明。lhs_proof和rhs_proof:左右两侧的证明,均包含公共输入数据。public_values:当前需要更新的公共值。
返回值:
- 聚合后的证明 (
ProofWithPublicInputs)。 - 更新后的公共值。
其具体的代码分析如下所示
3.1 初始化部分的 PartialWitness
let mut agg_inputs = PartialWitness::new();PartialWitness 是证明系统中的一个核心结构,用于设置电路中的变量值(Witness)。
这里初始化了一个空的 PartialWitness 对象,用来存储聚合证明电路的输入数据。
3.2 设置左侧证明的输入
agg_inputs.set_bool_target(self.aggregation.lhs.is_agg, lhs_is_agg);
agg_inputs.set_proof_with_pis_target(&self.aggregation.lhs.agg_proof, lhs_proof);
agg_inputs.set_proof_with_pis_target(&self.aggregation.lhs.evm_proof, lhs_proof);set_bool_target:
- 将左侧证明是否为聚合证明(
lhs_is_agg)写入电路的目标变量self.aggregation.lhs.is_agg。 - 这是一个布尔值,表示左侧证明的类型。
set_proof_with_pis_target:
- 设置左侧证明的聚合证明目标
self.aggregation.lhs.agg_proof。 - 同时将该证明写入以太坊验证目标
self.aggregation.lhs.evm_proof。 - 这两步将左侧证明和公共输入信息绑定到电路中。
3.3 设置右侧证明的输入
agg_inputs.set_bool_target(self.aggregation.rhs.is_agg, rhs_is_agg);
agg_inputs.set_proof_with_pis_target(&self.aggregation.rhs.agg_proof, rhs_proof);
agg_inputs.set_proof_with_pis_target(&self.aggregation.rhs.evm_proof, rhs_proof);类似于左侧的设置,右侧证明的输入也被写入目标:
- 布尔值
rhs_is_agg表示右侧证明是否是聚合证明。 rhs_proof被分别写入聚合证明目标和以太坊验证目标。
3.4. 设置验证数据(Verifier Data)
agg_inputs.set_verifier_data_target(
&self.aggregation.cyclic_vk,
&self.aggregation.circuit.verifier_only,
);set_verifier_data_target:
- 设置验证器的数据目标(
verifier data targets)。 self.aggregation.cyclic_vk是循环验证密钥,用于验证递归的聚合证明。self.aggregation.circuit.verifier_only提供电路中的验证器专属数据。
3.5. 设置公共值目标
set_public_value_targets(
&mut agg_inputs,
&self.aggregation.public_values,
&public_values,
)
.map_err(|_| {
anyhow::Error::msg("Invalid conversion when setting public values targets.")
})?;set_public_value_targets:
- 将传入的公共值(
public_values)映射到电路中的目标公共值(self.aggregation.public_values)。 - 如果发生映射错误,返回一个错误消息。
3.6 生成聚合证明
let aggregation_proof = self.aggregation.circuit.prove(agg_inputs)?;调用电路生成证明:
- 使用
self.aggregation.circuit对设置好的agg_inputs进行证明。 - 返回一个聚合后的证明对象
aggregation_proof。
3.7 返回聚合结果
Ok((aggregation_proof, public_values))
- 返回结果是:
- 生成的聚合证明
aggregation_proof。 - 更新后的公共值
public_values。
- 生成的聚合证明
4. 函数prove_root
这个函数的主要目的是对某个表(table)的证明数据进行处理,生成递归证明的根证明(Root Proof),它结合了 STARK 证明和 zkSNARK 的电路证明,将 STARK 证明压缩并整合到递归证明电路中,整体流程如下:
- 生成 STARK 证明:
- 使用
prove生成 STARK 证明。 - 验证生成的 STARK 证明,确保其正确性。
- 使用
- 压缩每个表的证明:
- 遍历每个表格,提取表对应的 STARK 证明。
- 压缩证明以适配递归电路。
- 设置递归电路目标:
- 将验证数据索引、压缩证明和公共值设置到递归电路目标。
- 生成根证明:
- 调用递归电路的
prove方法生成根证明。
- 调用递归电路的
- 返回结果:
- 返回生成的根证明和公共值。
函数定义
pub fn prove_root(
&self,
all_stark: &AllStark<F, D>, // STARK 证明配置
kernel: &Kernel, // 核心处理的内核
config: &StarkConfig, // STARK 配置
timing: &mut TimingTree, // 时间跟踪器
) -> anyhow::Result<(ProofWithPublicInputs<F, C, D>, PublicValues)>输入参数:
all_stark:表示所有 STARK 的配置,用于控制证明生成。kernel:核数据,包含表、内核的计算逻辑。config:STARK 配置,指定了一些证明相关的参数。timing:计时器,用于跟踪操作耗时。
返回值:
- 根证明(
ProofWithPublicInputs),包含公共输入。 - 更新后的公共值(
PublicValues)。
以下进行函数实现分步分析
4.1 生成 STARK 证明并验证
let all_proof = prove::<F, C, D>(all_stark, kernel, config, timing)?;
verify_proof(all_stark, all_proof.clone(), config).unwrap();- 生成 STARK 证明:
- 使用
prove函数基于all_stark和kernel的输入生成 STARK 证明all_proof。 - 这个证明包含了所有 STARK 表格的证明和公共输入。
- 验证 STARK 证明:
- 调用
verify_proof验证生成的 STARK 证明,确保证明正确。 - 如果验证失败,
unwrap会导致程序 panic(这表明验证是必须通过的)。
4.2 初始化根证明的输入
let mut root_inputs = PartialWitness::new();创建 PartialWitness 对象,用于后续为递归电路设置输入。
4.3 遍历所有表格
for table in 0..NUM_TABLES {
let stark_proof = &all_proof.stark_proofs[table];
let original_degree_bits = stark_proof.proof.recover_degree_bits(config);遍历所有表格(NUM_TABLES),每个表格都有一个对应的 STARK 证明。
调用 recover_degree_bits 从证明中恢复原始的多项式阶数。
4.4 缩减 STARK 证明
let table_circuits = &self.by_table[table];
let shrunk_proof = table_circuits
.by_stark_size
.get(&original_degree_bits)
.ok_or_else(|| {
anyhow::Error::msg(format!(
"Missing preprocessed circuits for {:?} table with size {}.",
Table::all()[table],
original_degree_bits,
))
})?
.shrink(stark_proof, &all_proof.ctl_challenges)?;获取电路:从预处理电路 self.by_table[table].by_stark_size 中获取对应阶数的电路。
缩减证明:调用 shrink 函数压缩 STARK 证明,使其适配递归电路。
- 输入
stark_proof和控制挑战(ctl_challenges)。 - 输出的
shrunk_proof是更小的证明,适合递归使用。
其中shrink 函数的核心作用是将一个大的 STARK 证明压缩成一个更小的证明,以适配递归证明的计算需求,同时保持原始证明的完整性和真实性。这个过程不仅减少了证明的复杂度,也提升了后续递归电路处理的效率,其具体过程如下:
- 首先,
shrink会调用initial_wrapper中的证明函数,对 STARK 证明进行初步压缩。这一步是关键,负责将原始的较大证明映射到一个较小的电路中。 - 接着,它会循环调用
shrinking_wrappers中的每个递归电路,将初步压缩后的证明继续逐步压缩,直到其大小符合目标电路的约束(例如THRESHOLD_DEGREE_BITS的递归门大小)。 - 返回一个最终压缩的
ProofWithPublicInputs结构体,这个结构体包含了公共输入和压缩后的证明,能够被更小的递归电路直接使用。
fn shrink(
&self,
stark_proof_with_metadata: &StarkProofWithMetadata<F, C, D>,
ctl_challenges: &GrandProductChallengeSet<F>,
) -> anyhow::Result<ProofWithPublicInputs<F, C, D>> {
let mut proof = self
.initial_wrapper
.prove(stark_proof_with_metadata, ctl_challenges)?;
for wrapper_circuit in &self.shrinking_wrappers {
proof = wrapper_circuit.prove(&proof)?;
}
Ok(proof)
}4.5 设置目标值
Target: 在电路中,Target 就是对“线”(wire)和“门”(gate)的抽象理解,可以简单理解为电路中“某个位置”的标记。它既可以表示某条线上的值,也可以表示某个门操作的位置。这样通过 Target,我们可以方便地操作和引用电路中的某些数据或操作,尤其是在复杂的递归验证或者跨表操作中,用 Target 可以让整个设计更简单、更清晰。
let index_verifier_data = table_circuits
.by_stark_size
.keys()
.position(|&size| size == original_degree_bits)
.unwrap();
root_inputs.set_target(
self.root.index_verifier_data[table],
F::from_canonical_usize(index_verifier_data),
);
root_inputs.set_proof_with_pis_target(&self.root.proof_with_pis[table], &shrunk_proof);设置验证数据索引:找到原始阶数对应的验证数据索引,将其设置为递归电路的目标值。
设置压缩证明:将缩减后的证明设置到递归电路目标中。
4.6 设置循环验证数据
root_inputs.set_verifier_data_target(
&self.root.cyclic_vk,
&self.aggregation.circuit.verifier_only,
);将循环验证密钥(cyclic_vk)绑定到递归电路的验证数据目标。
4.7 设置公共值
set_public_value_targets(
&mut root_inputs,
&self.root.public_values,
&all_proof.public_values,
)
.map_err(|_| {
anyhow::Error::msg("Invalid conversion when setting public values targets.")
})?;将 STARK 证明中的公共值映射到递归电路的公共值目标。
如果映射失败,返回错误信息。
4.8 生成根证明
let root_proof = self.root.circuit.prove(root_inputs)?;调用递归电路的 prove 函数,基于 root_inputs 生成根证明。
4.9 返回根证明和公共值
Ok((root_proof, all_proof.public_values))返回生成的根证明 root_proof 和 STARK 证明的公共值。
