可信设置如何运作？

如何进行可信设置？

必要背景：椭圆曲线和椭圆曲线配对。另请参见：Dankrad Feist 的 KZG 多项式承诺文章。

特别感谢 Justin Drake、Dankrad Feist 和 Chih-Cheng Liang 的反馈和审阅。

许多加密协议，尤其是在数据可用性采样和ZK-SNARKs领域，依赖于可信设置。可信设置仪式是一种只需执行一次的程序，用于生成一段数据，该数据必须在每次运行某些加密协议时使用。生成该数据需要一些机密信息；信任来自于某个人或某一群体必须生成这些机密，使用它们生成数据，然后发布数据并忘记这些机密。但一旦数据生成并且机密被遗忘，就不再需要仪式参与者的进一步参与。

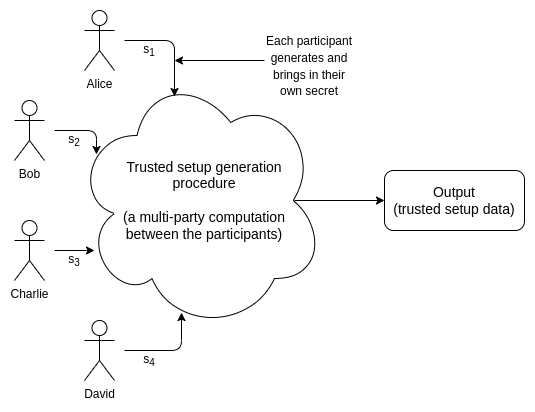
有许多类型的可信设置。首次在主要协议中使用可信设置的实例是2016年的原始 Zcash 仪式。该仪式非常复杂，需要多轮通讯，因此只能有六位参与者。此时使用 Zcash 的每个人实际上都信任六位参与者中至少有一位是诚实的。更现代的协议通常使用tau 的幂设置，该设置具有1-of-N 信任模型，其中 N 通常在几百左右。也就是说，数百人共同参与生成数据，只有其中一人需要诚实并且不发布他们的机密，以使最终输出安全。执行良好的设置通常被认为在实践中是“足够接近无信任”的。

本文将解释 KZG 设置的工作原理、其运作原因以及可信设置协议的未来。任何熟悉代码的人也可以跟随以下代码实现：<https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py>。

tau 的幂设置是怎样的？

tau 的幂设置由两个系列的椭圆曲线点组成，如下所示：

[G1,G1∗s,G1∗s2...G1∗sn1−1]

[G2,G2∗s,G2∗s2...G2∗sn2−1]

G1 和 G2 是两个椭圆曲线组的标准化生成点；在 BLS12-381 中，G1 点是（以压缩形式）48 字节长，而 G2 点是 96 字节长。n1 和 n2 是设置中 G1 和 G2 侧的长度。一些协议要求 n2=2，其他协议则要求 n1 和 n2 都很大，还有一些处于中间（例如，当前形式的以太坊数据可用性采样要求 n1=4096 和 n2=16）。s 是用于生成点的机密，且需被遗忘。

为了对多项式 P(x)=∑icixi 进行 KZG 承诺，我们只需取线性组合 ∑iciSi，其中 Si=G1∗si（在可信设置中的椭圆曲线点）。设置中的 G2 点用于验证我们承诺的多项式的评估；在此我不会详细讨论验证过程，但Dankrad 在他的文章中有所涉及。

从直观上讲，可信设置提供了什么价值？

了解这里的哲学含义，以及可信设置提供的价值是很重要的。多项式承诺是对大小为 N 的数据进行承诺，使用大小为 O(1) 的对象（一个单一的椭圆曲线点）。我们可以使用简单的 Pedersen 承诺来实现此目的：将 Si 的值设置为 N 个随机椭圆曲线点，彼此之间没有已知关系，然后像之前一样对多项式进行承诺 ∑iciSi。实际上，这正是IPA 评估证明所做的。

然而，任何基于 IPA 的证明都需要 O(N) 的验证时间，这是有不可避免的原因的：对多项式 P(x) 使用基点 [S0,S1...Si...Sn−1] 进行承诺，如果我们使用基点 [S0,S1...(Si∗2)...Sn−1]，则将承诺另一个多项式。

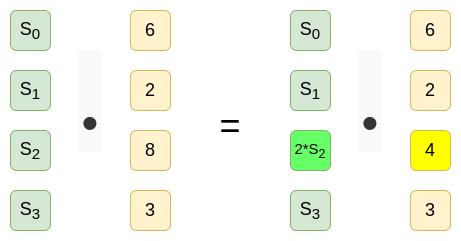
如果我们想为某个陈述（例如，这个多项式在 x=10 时的值为 3826）制作一个基于 IPA 的证明，该证明应该在第一组基点上通过，而在第二组上失败。因此，不管证明验证程序是什么，无法避免以某种方式考虑每一个 Si 值，因此它不可避免地需要 O(N) 的时间。

但通过可信设置，点之间存在隐藏的数学关系。可以保证 Si+1=s∗Si，两个相邻点之间有相同的因子 s。如果 [S0,S1...Si...Sn−1] 是一个有效的设置，那么“编辑后的设置” [S0,S1...(Si∗2)...Sn−1] 不能也是有效的设置。因此，我们不需要 O(n) 的计算；相反，我们利用这个数学关系以常数时间验证我们需要验证的任何内容。

但是，这种数学关系必须保持秘密：如果知道 s，那么任何人都可以提出一个承诺，表示多种不同的多项式：如果 C 承诺 P(x)，它也承诺 P(x)∗xs，或者 P(x)−x+s，或者许多其他形式。这会完全破坏多项式承诺的所有应用。因此，在某个时刻必须存在某个秘密 s，以使 Si 值之间的数学联系能够实现高效验证，而 s 也必须被遗忘。

多参与者设置是如何工作的？

很容易看出，一个参与者如何生成设置：只需选择一个随机 s，并使用该 s 生成椭圆曲线点。但单个参与者的可信设置是不安全的：你必须信任特定的个人！

解决方案是多参与者可信设置，所谓“多参与者”指的是_许多_参与者：通常超过 100，针对较小的设置有可能超过 1000。多参与者的 tau 的幂设置工作如下。

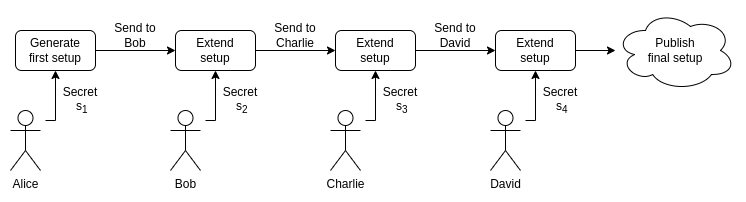
从现有设置中取值（请注意，你不知道 s，只知道这些点）：

[G1,G1∗s,G1∗s2...G1∗sn1−1]

[G2,G2∗s,G2∗s2...G2∗sn2−1]

现在，选择自己的随机机密 t。计算：

[G1,(G1∗s)∗t,(G1∗s2)∗t2...(G1∗sn1−1)∗tn2−1]

[G2,(G2∗s)∗t,(G2∗s2)∗t2...(G2∗sn2−1)∗tn2−1]

请注意，这与以下内容是等同的：

[G1,G1∗(st),G1∗(st)2...G1∗(st)n1−1]

[G2,G2∗(st),G2∗(st)2...G2∗(st)n2−1]

也就是说，你已经用机密 s∗t 创建了一个有效的设置！你从未向以前的参与者提供你的 t，先前的参与者也没有向你提供他们用于 s 的秘密。只要有任何一个参与者保持诚实并不透露他们的机密部分，组合秘密就不会被披露。特别地，有限域具有这样的特性：如果你知道 s 而不知道 t，而 t 是安全随机生成的，那么你对 s∗t 毫无所知！

验证设置

为了验证每个参与者实际上参与了，每个参与者可以提供一个证明，该证明由 (i) 他们收到的 G1∗s 点以及 (ii) G2∗t 组成，其中 t 是他们引入的机密。这些证明的列表可以用来验证最终设置是否结合了所有机密（相对于例如最后一位参与者忘记之前的值并仅输出他们自己保留的机密的设置，以便在任何使用该设置的协议中进行作弊）。

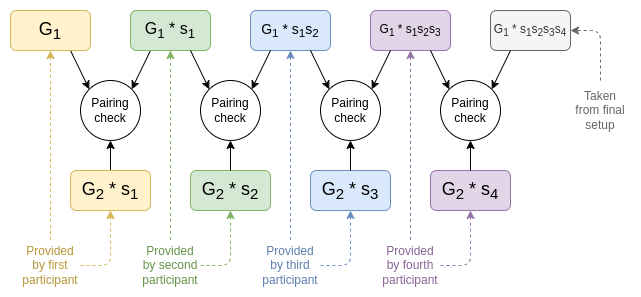
每个参与者应在某个公开可验证的媒体（例如个人网站、来自其 .eth 地址的交易、Twitter）上公开其证明。请注意，这种机制并不防止某人声称自己在其他人参加的某个索引处参与（假设其他人已经披露了他们的证明），但通常认为这没有关系：如果某人愿意撒谎称参与，他们也会愿意撒谎称他们已删除秘密。只要至少有一位那些声称已参与的人诚实，设置就是安全的。

除了上述检查之外，我们还希望验证设置中的所有幂是否正确构建（即它们都是同一秘密的幂）。为此，我们_可以_进行一系列配对检查，验证对于每一个 i，e(Si+1,G2)=e(Si,T1)（其中 T1 是设置中的 G2∗s 值）。这验证了每个 Si 和 Si+1 之间的因子与 T1 和 G2 之间的因子相同。然后对 G2 侧进行相同的处理。

但这需要很多配对且费用昂贵。相反，我们取一个随机线性组合 L1=∑i=0n1−2riSi，并将同一线性组合向前平移一位：L2=∑i=0n1−2riSi+1。我们使用一次配对检查来验证它们是否匹配：e(L2,G2)=e(L1,T1)。

我们甚至可以将 G1 侧和 G2 侧的过程结合在一起：在计算 L1 和 L2 的同时，我们也计算 L3=∑i=0n2−2qiTi（qi 是另一组随机系数）和 L4=∑i=0n2−2qiTi+1，并检查 e(L2,L3)=e(L1,L4)。

拉格朗日形式的设置

在许多用例中，你不想使用多项式的系数形式（例如 P(x)=3x^3+8x^2+2x+6），你想使用多项式的评估形式（例如在模 337 的域 [1,189,336,148] 上，P(x) 这个多项式的值为 [19,146,9,187]）。评估形式具有许多优点（例如，你可以在 O(N) 时间内相乘和有时相除多项式），你甚至可以用它在 O(N) 时间内进行评估。特别是，数据可用性采样 期望这些数据在评估形式中。

为了处理这些情况，通常将可信设置转换为评估形式是便利的。这将使你能够直接将评估（上述示例中的 [19,146,9,187]）用于计算承诺。

通过快速傅里叶变换（FFT）最容易实现这种转换，但将曲线点作为输入而不是数字。在此我将避免重复详细解释 FFT，但这里有一个实现；其实并不难。

可信设置的未来

tau 的幂并不是唯一的可信设置。其他一些显著的（实际或潜在的）可信设置包括：

• 更复杂的旧 ZK-SNARK 协议中的设置（例如，见这里），某些情况下仍然使用（特别是 Groth16）因为验证比 PLONK 便宜。
• 一些加密协议（例如DARK）依赖于隐藏阶群，这类群的元素无法确定是什么数字可以被乘以得到零元素。此类群体存在完全无信任的版本（见：类群），但最有效的版本使用 RSA 群（x 的幂 mod n=pq，其中 p 和 q 是未知的）。拥有 1-of-n 信任假设的可信设置仪式是可行的，但实现起来非常复杂。
• 如果/当不可区分混淆变得可行时，许多依赖于它的协议将涉及与隐藏内部秘密的程序相关的人创建和发布混淆程序。这是一个可信设置：创建者必须拥有该机密以创建程序，并且还需要在之后删除它。

加密学仍然是一个快速发展的领域，可信设置的重要性可能轻易发生变化。技术可能会改进到足以让 KZG 变得过时和不必要，或者量子计算机可能会在十年内使基于椭圆曲线的任何内容不再可行，我们将被迫使用无可信设置的基于哈希的协议。也可能的是，我们可以使用 KZG 的能力可能更快地改进，或者新的加密领域会出现，这可能依赖于不同类型的可信设置。

在可信设置仪式是必要的情况下，重要的是要记住并非所有可信设置都是平等创造的。176 个参与者 总比 6 个要好，2000 还会更好。一个设置足够小，可以在浏览器或手机应用程序内运行（例如，ZKopru 设置是基于网络的），可以吸引比需要运行复杂软件包的设置更多的参与者。每个仪式理想情况下应有多个独立构建的软件实现的参与者，并运行不同的操作系统和环境，以降低共通模式故障的风险。每位参与者只需进行一轮交互的仪式（如 tau 的幂）远远好于多轮仪式，这既可以支持更多的参与者，又更容易编写多个实现。仪式应该理想上是通用的（一次仪式的输出能够支持多种协议）。这些都是我们可以并且应该继续努力的事情，以确保可信设置可以尽可能安全和可信。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～