密码学第一准则……不要讨论零值或单位元

密码学的第一条规则……不要谈论零或单位元

好的，很抱歉引用了《搏击俱乐部》！总的来说，这个标题有点半开玩笑，因为零值在密码学中通常是一个主要问题，而且我们通常不希望它发生。对于安全架构师和开发人员来说，它也可能是一个盲点，他们在实现计算时没有检查零值。

为什么零是一个问题？ 嗯，为了执行我们的密码学处理，我们使用数学运算，例如乘法和除法。你应该记得，当我们乘以零时，我们得到零，当我们除以零时，我们得到无穷大。这些操作会重置计算，无论我们做什么，我们都无法从我们的值中恢复任何先前的信息。我们可能还会使用指数，其中 g⁰ 给了我们单位值。

在我们的安全计算中，我们通常需要将操作反转回原始值。这通常涉及加密——执行某种数学运算——然后解密——反转相同的数学运算。

例如，如果我们将七乘以四，然后加三，我们可以计算：

Val = 7 * 4 + 3 = 31

并且，为了反转，我们只需减去 3 并除以 4：

Res = (31 - 3) / 4 = 7

但是，如果我乘以零，然后加三：

Val = 7 * 0 + 3 = 3

并反转：

Val = (3 - 3) / 0 = 无穷大（或者，谁知道，因为它是 0/0！）

因此，我们经常希望避免零值，因为它会短路我们所有的计算并导致严重错误。零成为重置值，所有先前计算的值都将丢失。因此，我们的计算应始终检查我们是否没有零值；否则，我们得到的所有答案都可能是错误的。更糟糕的是，我们可能会继续进行计算并获得肯定的答案，例如错误地签署数据。在签名中，我们经常比较两个值，但是公钥的零值可能会导致签名无效。

椭圆曲线中的单位元

单位元被称为椭圆曲线上加减运算的“无穷远点”。对于整数的元素 (E)，单位元 (I) 的一些规则是：

E + I = E

以及：

E - E = I

在整数值中，值 0（零）符合这些标准，但是椭圆曲线呢？对于椭圆曲线，对于一个点 (P) 和无穷远点 (O)，我们得到：

P + O = P

以及：

P - P = O

如果我们将标量值乘以单位元，则得到单位元：

n.I = I

如果我们尝试 (0,1) 点 [ 这里]：

package main

import (
 "fmt"
 "github.com/iden3/go-iden3-crypto/v2/babyjub"
 "math/big"

 "math/rand"

)

func main() {

 x,_ := new(big.Int).SetString("0",10 )
 y,_ := new(big.Int).SetString("1",10)

 P := &babyjub.Point{X: x, Y: y}

 fmt.Printf("P (%s, %s)\n",P.X.String(),P.Y.String())

 fmt.Printf("Point valid: %v\n",P.InCurve())

 s:=new(big.Int).SetInt64(int64(rand.Intn(1000)))
  sP := babyjub.NewPoint().Mul(s, P)

 fmt.Printf("(%d).P Point (%s, %s)\n",s,sP.X.String(),sP.Y.String())

}

结果是 [ 这里]：

P (0, 1)
Point valid: true
(318).P Point (0, 1)

我们可以看到，尽管我们将单位元乘以 318，但我们仍然得到单位元作为结果。无论我们将单位元乘以什么，我们总是会得到单位元（又名无穷远点）。

在离散对数中阻止零值

在有限域中，我们经常使用 (mod p) 运算，其中 p 是一个素数。因此，如果我们得到一个 p 的倍数的值，我们也会得到一个零值。如果 p 是 7，并且如果我们的消息是 14，我们将得到：

Val = 14 (mod 7) = 0

这将等于零，我们将无法恢复我们的值。为此，在离散对数中，我们有：

Val = g^x (mod p)

其中我们选择 g（生成器），以便我们永远不会有零值。因此，如果我们有 p=7，并且可以尝试不同的生成器值 [ 这里]：

Zoom image will be displayed

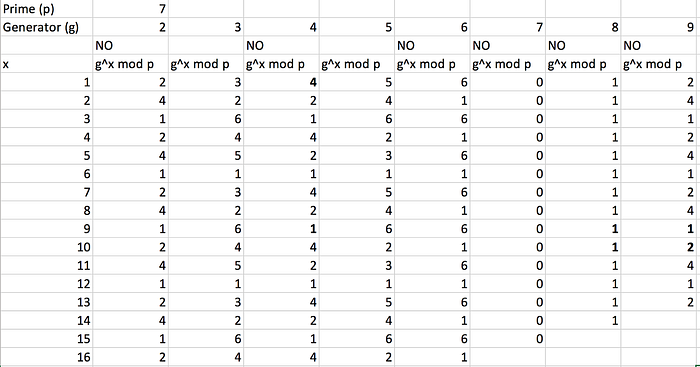
我们可以看到，g=2 的值不适用于 p=7，因为我们没有输出完整的值范围（1 到 6），但 g=3 有效，因为：

3¹ (mod 7) = 1

3² (mod 7) = 2

3³ (mod 7) = 6

等等。然后我们将能够将所有这些值映射回原始值，从而反转这些值。因此，开发人员应在重要时刻检查他们是否没有得到零值，并且是否正确选择了基本生成器。

当然，伊芙不遵守规则，可能会诱骗Bob短路他的密码学过程。

椭圆曲线中的零

我们通常已经从离散对数方法转移到椭圆曲线技术，在椭圆曲线技术中，我们处理标量值和椭圆曲线点。如果我的私钥是 a，那么我的公钥可以是 a.G，其中 G 是曲线上基点。这基本上是 G+G+G … +G，其中点 G 被加了 a 次。总的来说，如果我们有 a.G 和 G，那么确定 a 是非常困难的。

但是，椭圆曲线也有一个零问题。如果取一个点 p1，然后取 -p1，那么这些点的和将是：

p = p1 - p1 = 𝑂

这是零点，也被定义为无穷远点。在大多数椭圆曲线中，我们基本上只是否定 y 坐标值，并保持 x 坐标值不变。伊芙可能会诱骗Bob使用一个她可以轻易破解的弱生成器值。

现在让我们看一个创建零点的严重例子，这可能会危及电子钱包。

流氓公钥

使用 BN256，我们从一个随机数创建私钥。这是一个标量值（_sk_1），一个映射到 G2 曲线的公钥：

在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的故事

免费加入 Medium，获取这位作者的更新。

_pub_1 = _sk_1. _G_2

接下来，我们创建消息的哈希值（H(M))，然后创建签名：

_σ_1 = _sk_1. H(M)

接下来，我们检查这个对：

e(_σ_1, _G_2) == e(H(m), _pk_1)

这起作用是因为：

e(_σ_1, _G_2) == e(H(m), _pk_1)

是：

e(x. H(M), _G_2) == e(H(m), _pk_1)

以及：

e(H(M), x. _G_2) == e(H(m), _pk_1)

即：

e(H(M), _pk_1) == e(H(m), _pk_1)

如果 lhs 等于 rhs，则配对有效，并且签名已验证。

现在我们可以聚合签名。对于第二组密钥，我们现在有一个公钥：

_pub_2 = _sk_2. _G_2

其中第二个签名将是：

_σ_2 = _sk_2. H(M)

然后，聚合的公钥将是：

_pk_a = _pub_1 + _pub_2

然后，聚合的签名将是：

_σ_a = _σ_1 + _σ_2

检查是：

e(σa, _G_2) == e(H(m), _pka)

在流氓公钥攻击中，伊芙可以通过创建一个公钥来假装她正在签署消息：

_pub_2 = - _pub_1

以及签名：

_σ_2 = - _σ_1

负值很容易实现，因为我们只需要使 y 轴值为负，并且可以保持 x 轴值不变。如果Bob和伊芙正在签署消息 (M)，Bob将传递 _pk_1 和 _σ_1，伊芙将创建这些的负值，并传递 _pk_2 = - _pk_1 和 _σ_2 = - _σ_1。当公钥和签名聚合时，我们将得到一个零值。因此：

_pk_a = 0

_σ_a = 0

对聚合签名的检查将是：

e(σa, _G_2) == e(H(m), _pka)

即：

e([0]. _G_1, _G_2) == e(H(m), [0]. _G_2)

这将与以下相同：

e([0]. _G_1, _G_2) == e([0]. H(m), _G_2)

这将与以下相同：

e([0], _G_2) == e([0], _G_2)

因此，如果未检查零聚合，则测试将通过。伊芙因此签署了一条她对其内容一无所知的消息。因此，我们应始终检查公钥和/或签名中是否存在零值，如果为零则拒绝它们。

编码

接下来给出了 Go 代码的概述[ 这里]，并高亮显示了聚合部分：

package main

import (
    "bytes"
    "fmt"
    "math/big"
    "os"
    "crypto/rand"

    "github.com/cloudflare/bn256"
)

func main() {

    salt := []byte{11, 12, 13, 14}
    message:="Hello"
    argCount := len(os.Args[1:])
    if argCount > 0 {
        message = os.Args[1]
    }
    msg := []byte(message)
    G2 := new(bn256.G2).ScalarBaseMult(big.NewInt(1))
    privKey, _, _ := bn256.RandomG2(rand.Reader)
    pubKey := new(bn256.G2).ScalarBaseMult(privKey)
    hash := bn256.HashG1(msg, salt)
    sigma := new(bn256.G1).ScalarMult(hash, privKey)
    rhs := bn256.Pair(hash, pubKey)
    lhs := bn256.Pair(sigma, G2)

    fmt.Printf("Message: %s\n", message)
    fmt.Printf("Private key 1: %x\n", privKey)
    fmt.Printf("\nPublic key 1: %x\n", pubKey.Marshal())
    fmt.Printf("\nSignature (sigma): %x\n", sigma.Marshal())

    if bytes.Equal(rhs.Marshal(), lhs.Marshal()) {
        fmt.Printf("\nSignature verified!\n")
    }

    betapubKey:= new(bn256.G2).ScalarBaseMult(privKey)
        betapubKey.Neg(betapubKey)
    pub_aggr := pubKey.Add(pubKey, betapubKey)
    sigma2 := new(bn256.G1).ScalarMult(hash, privKey)
    sigma2.Neg(sigma2)
    sigma_aggr :=sigma.Add(sigma, sigma2)

    fmt.Printf("Private key 2: %x\n", privKey)
    fmt.Printf("\nPublic key 2: %x\n", betapubKey.Marshal())
    fmt.Printf("\nSignature (sigma2): %x\n", sigma2.Marshal())

    fmt.Printf("\nSignature aggregated: %x\n", sigma_aggr.Marshal())
    fmt.Printf("\nPublic key aggregated: %x\n", pub_aggr.Marshal())

    rhs = bn256.Pair(hash, pub_aggr)
    lhs = bn256.Pair(sigma_aggr, G2)

    if bytes.Equal(rhs.Marshal(), lhs.Marshal()) {
        fmt.Printf("\nAggregated Signature verified!")
    }

}

一个示例运行是 [ 这里]。请注意，聚合的公钥和签名值已设置为零：

Message: abc
Private key 1: 896c9dcfea9659ea00bfc1ddd97c98271febc873119babd25d25de4ac46968b8
Public key 1: 01026c76c9a917726c83f8748301e39bb34553b59f1877281085cafae9e2ea9499837e91ef55b8f7657ce38bec5c343213f43b96385ad78fbcc298484d1f8aab3e3dbef72f2a43420435239aaca8f34557e616988413df15cf60cc12fc94b867824905b9d1d61c7bb51d593f149ffba192a84ecbc55624b6b6bb8120be579a081a
Signature (sigma): 48385fd0e9f6b1a97ddc1a408bad6e806bae49b13121d84a0e07d5d4ec59fb8c325bb417ef4ca540488577ac061445dfb073ce4a698754e3d12c8801593be09f
Signature verified!
Private key 2: 896c9dcfea9659ea00bfc1ddd97c98271febc873119babd25d25de4ac46968b8
Public key 2: 01026c76c9a917726c83f8748301e39bb34553b59f1877281085cafae9e2ea9499837e91ef55b8f7657ce38bec5c343213f43b96385ad78fbcc298484d1f8aab3e51f60ab4206045f5754c520bb89196ca0844f04d0cd69fceb790996fc9502ee546af481174870c448d16ada3c1893a8f460cbd0bca90fee75cdb8bae066e8e4d
Signature (sigma2): 48385fd0e9f6b1a97ddc1a408bad6e806bae49b13121d84a0e07d5d4ec59fb8c5d594dcb5b56e2b961ea750c5b7096423de7ba86b72e60ba4730246b04ccb5c8
Signature aggregated: 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Public key aggregated: 00
Aggregated Signature verified!

我们可以看到伊芙已经获得了Bob的公钥，并且不知道她正在签署的消息。然后她创建了他的值的负值，并传递该值以及签名的负值。当特伦特检查签名时，看起来Bob和伊芙都已签署了该消息。也许这可能是为了将一些加密货币从Bob转移到伊芙？

结论

密码学的第一条规则是，我们需要谈论零值。开发人员需要接受培训，以便在计算中发现它，因为伊芙并不总是遵守规则。

这是流氓公钥攻击：

https://asecuritysite.com/bn/bls_sig3

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～