Uniswap 没有市场深度，即买即卖的去中心化交易所

outprog
更新于 2018-11-18 11:33
阅读 3827

Uniswap 实现了一种不需要考虑以上特点的去中心化交易所。它不需要用户进行挂单（没有订单），不需要存在需求重叠，可以随买随卖。得益于 ERC20 代币的特性，它也不需要用户将资产存入特定的账户（如中心化交易所的银行账户或者智能合约等，资产的存储位置不是本文讨论的重点）。

**本文需要读者对[区块链](https://learnblockchain.cn/2019/10/30/whatblockchain)、[以太坊](https://learnblockchain.cn/2017/11/20/whatiseth)和[智能合约](https://learnblockchain.cn/2018/01/04/understanding-smart-contracts)有一定的基础。需要对交易所有一定的认知。*

区块链对实体性质的事物影响会滞后于对虚拟性质的事物，在区块链上最先能发展起来的事物必定是形而上的。那些我们看不见摸不着的“体系”、“制度”甚至是“法律”，会最快的在区块链上试验，其中货币和交易所是这些试验的先行者。

上次我简单介绍了 Basis，一个在区块链上基于中央银行协议实现稳定数字货币的项目（[Basis，去中心化央行？](https://learnblockchain.cn/article/1115)），这次我们来看看交易所在区块链上的一种实现。

> 传统的交易所一般是提供一个挂单平台，通过程序（撮合引擎）撮合买卖双方达成交易。它是一个自由买卖的市场，具有买卖意愿的人们自行挂出“买单”和“卖单”，通过交易所“中介”实现双方订单的成交。传统交易所有以下特点：
>
>
> 1. 市场上必须要有用户进行挂单，要有一定量的订单（市场深度）。
>
> 1. 订单必须重叠才能成交，即买价高于或等于卖价。
>
> 1. 需要将资产存储在交易所。
>

### 乘积恒定的稳定系统

Uniswap 的运行机制的关键在于建立了供给池，这个供给池中存储了 A 和 B 两种货币资产。用户在用 A 兑换 B 的过程中，用户的 A 会发送到供给池，使供给池中的 A 增多，同时，供给池的 B 会发送给用户。这里的关键的问题在于如何给 A 和 B 的兑换提供一个汇率（定价）。

Uniswap 定价模型非常简洁，它的核心思想是一个简单的公式 `x * y = k` 。其中 x 和 y 分别代表两种资产的数量，k 是两种资产数量的乘积。

假设乘积 k 是一个固定不变的常量，可以确定当变量 x 的值越大，那么 y 的值就越小；相反 x 的值越小，y 的值就越大。据此可以得出当 x 被增大 p 时，需要将 y 减少 q 才能保持等式的恒定。

在 k 恒定的情况下，推导 q 的计算公式如下：

```e-undefined
x * y = k
(x + p) * (y - q) = k
q = y - k/(x + p)
```

其中，p 是 x 的增量，q 是 y 的减量。通过 k 的恒定不变就可以提供下图所示的稳定系统：

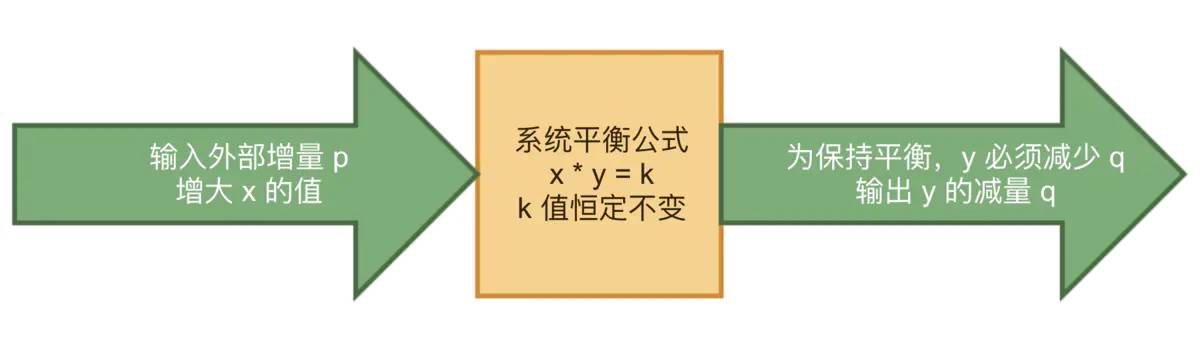
![111.jpg](https://img.learnblockchain.cn/attachments/2020/06/aGU5b1Sm5ee0910a86410.jpg)

由此我们已经有了一个数学上平衡稳定的系统。这个系统的目标是不管 x，y 分别是增加还是减少，必须要保证乘积 k 恒定。

### 实现兑换

为了做一些更实用的工作，将 x 和 y 替换为货币储备金的储备量，这些储备金将被存储在智能合约中。假设 x 是 USD 的储备量，数量为 100；y 是 CNY 的储备量，数量为 700，储备金的乘积就是 70000。

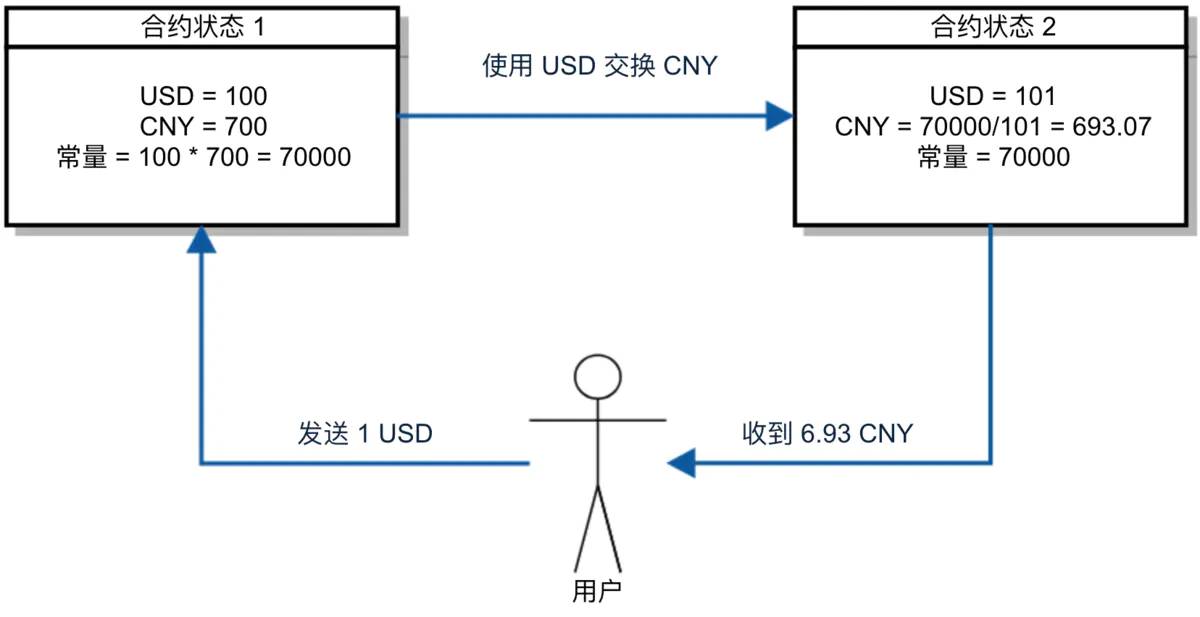
![222.jpg](https://img.learnblockchain.cn/attachments/2020/06/xNxCStVR5ee0914030d02.jpg)

用户向合约发送 1 USD，合约中的 USD 储备量就会增加，为了保证乘积 70000 不变，根据保证 k 恒定的公式计算出合约中应当减少的 CNY 的数量 q：

```e-bash
q = y - k/(x + p)
q = 700 - 70000/(100 + 1)
q = 6.93                    # 未完全精确计算
```

CNY 的减少数量 6.93 为用户使用 1 USD 兑换应得的 CNY。当用户需再次使用 1 USD 购买 CNY 时，根据 `合约状态 2` ，此时 USD 储备为 101，CNY 储备为 693.07， 可以计算出新的 CNY 的减量 q 为：

```e-undefined
q = 693.07 - 70000/(101 + 1)
q = 6.80
```

第二次兑换后，用户收到的 CNY 数量为 6.80，比第一次兑换所得 6.93 少。观察公式 `x * y = 70000` 曲线可以看出，随着 x 的增加，y 的变化率越来越小（曲线沿0 x 轴向右趋于平滑）。

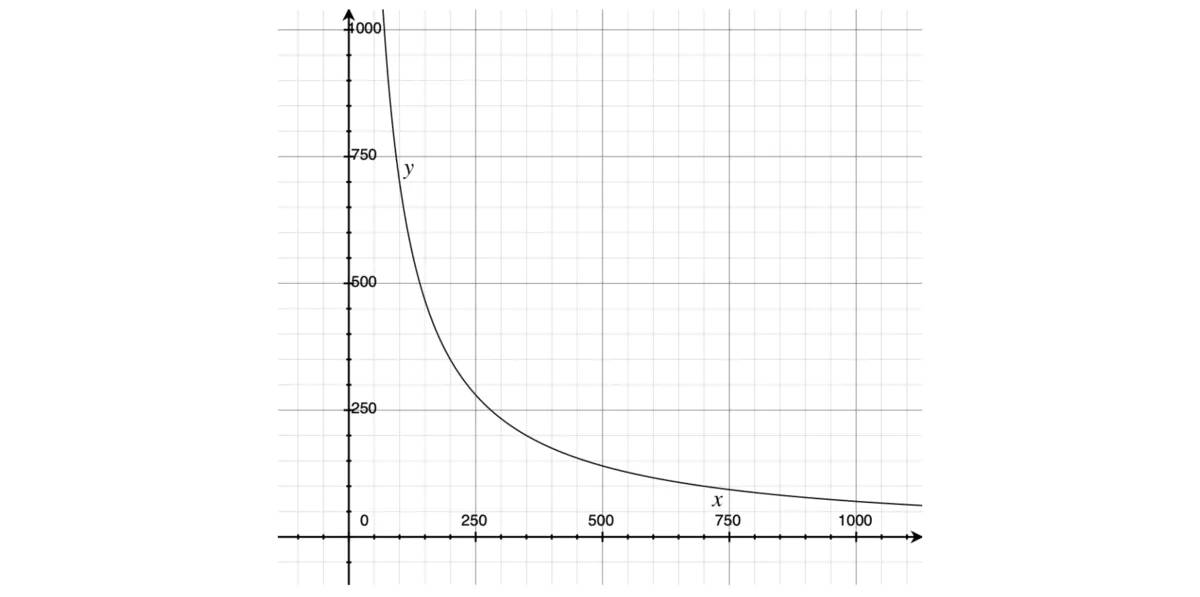
![333.jpg](https://img.learnblockchain.cn/attachments/2020/06/mjJsM5wf5ee09192010b7.jpg)

所以在使用 USD 购买 CNY 的过程中，由于 USD（x）储备量的增加，会使 CNY 变化率缩小，即 CNY 的价格会逐渐升高（price = 1/rate）；相反，用 CNY 购买 USD，就会使 USD 的价格逐渐升高。可以发现购买的过程符合经济学上的供需关系，即购买量越多，需求越旺盛，价格越高。

如果在 Uniswap 系统中 CNY 的价格高于市面价格，那么就会有人在 系统中出售 CNY 购买 USD，使 CNY 价格降低，反之亦然。通过这种反馈调节，智能合约产生的兑换汇率总是趋近于市场真实汇率。

实际的 Uniswap 与上述介绍还有所区别。交易费率、费率对“常数”的影响、任意 token 之间的兑换都不再上述讨论范围。然而非常明确的是，通过智能合约和数学公式可以实现不需要挂单、不需要“市场深度”、随买随卖的交易兑换系统。

### 中心化方式建立系统

读者会认为可以考虑使用传统中心化的手段建立这样的交易系统。考虑以下两点：

1. 成本：传统系统需要处理多方会计帐、风险控制、储备商接入、系统的安全等，构建成本高。区块链的智能合约和代币机制非常适合使用公式化手段建立系统，核心功能只需要百十行代码即可实现（构建系统的其他难点实际上被区块链底层解决）。

1. 地域性：传统系统的使用受到国家、地域限制，所支持的兑换货币能力也限制于地方政策法规。区块链构建的系统无边界，只需接入世界互联网即可使用（合约代码可以由任何人、任何机构编写，运行在整个区块网络上供任何人使用）。

### 优势和不足

Uniswap 模型的优点在于根据公式自动定价，通过供需关系实现自动调价。然而这也可能是模型的不足之处。自动反馈调节是把双刃剑，兑换的汇率需要根据合约中储备金的比例进行计算，意味着最终的成交价格与兑换的数量相关。当兑换的数量越大，兑换的汇率就会变得越差。这样所谓的即买即卖也可能变成“买不起”和“卖不起”。但这是市场供需关系的自然反馈，也许并不能算是缺陷。

然而更糟的是，假设一种货币价格持续降低，储备金中这种下跌货币的储备量就会持续增加。考虑合约中的储备金分别一种较好货币和一种处于泡沫中的较差货币，那么通过一段时间兑换后，整个储备系统的较好货币被兑出，剩下大量的泡沫货币。这对提供储备的储备商是一件非常糟糕的事。

关于 Uniswap 的介绍就到这里，欢迎对区块链和经济感兴趣的同学提出的你们宝贵的看法和见解。

### 参考

[Uniswap Whitepaper](https://hackmd.io/C-DvwDSfSxuh-Gd4WKE_ig)

*本文需要读者对区块链、以太坊和智能合约有一定的基础。需要对交易所有一定的认知。

上次我简单介绍了 Basis，一个在区块链上基于中央银行协议实现稳定数字货币的项目（Basis，去中心化央行？），这次我们来看看交易所在区块链上的一种实现。

传统的交易所一般是提供一个挂单平台，通过程序（撮合引擎）撮合买卖双方达成交易。它是一个自由买卖的市场，具有买卖意愿的人们自行挂出“买单”和“卖单”，通过交易所“中介”实现双方订单的成交。传统交易所有以下特点：

市场上必须要有用户进行挂单，要有一定量的订单（市场深度）。

订单必须重叠才能成交，即买价高于或等于卖价。

需要将资产存储在交易所。

乘积恒定的稳定系统

Uniswap 定价模型非常简洁，它的核心思想是一个简单的公式 x * y = k 。其中 x 和 y 分别代表两种资产的数量，k 是两种资产数量的乘积。

在 k 恒定的情况下，推导 q 的计算公式如下：

x * y = k
(x + p) * (y - q) = k
q = y - k/(x + p)

其中，p 是 x 的增量，q 是 y 的减量。通过 k 的恒定不变就可以提供下图所示的稳定系统：

由此我们已经有了一个数学上平衡稳定的系统。这个系统的目标是不管 x，y 分别是增加还是减少，必须要保证乘积 k 恒定。

实现兑换

用户向合约发送 1 USD，合约中的 USD 储备量就会增加，为了保证乘积 70000 不变，根据保证 k 恒定的公式计算出合约中应当减少的 CNY 的数量 q：

q = y - k/(x + p)
q = 700 - 70000/(100 + 1)
q = 6.93                    # 未完全精确计算

CNY 的减少数量 6.93 为用户使用 1 USD 兑换应得的 CNY。当用户需再次使用 1 USD 购买 CNY 时，根据 合约状态 2 ，此时 USD 储备为 101，CNY 储备为 693.07，可以计算出新的 CNY 的减量 q 为：

q = 693.07 - 70000/(101 + 1)
q = 6.80

第二次兑换后，用户收到的 CNY 数量为 6.80，比第一次兑换所得 6.93 少。观察公式 x * y = 70000 曲线可以看出，随着 x 的增加，y 的变化率越来越小（曲线沿0 x 轴向右趋于平滑）。

如果在 Uniswap 系统中 CNY 的价格高于市面价格，那么就会有人在系统中出售 CNY 购买 USD，使 CNY 价格降低，反之亦然。通过这种反馈调节，智能合约产生的兑换汇率总是趋近于市场真实汇率。

中心化方式建立系统

读者会认为可以考虑使用传统中心化的手段建立这样的交易系统。考虑以下两点：

成本：传统系统需要处理多方会计帐、风险控制、储备商接入、系统的安全等，构建成本高。区块链的智能合约和代币机制非常适合使用公式化手段建立系统，核心功能只需要百十行代码即可实现（构建系统的其他难点实际上被区块链底层解决）。
地域性：传统系统的使用受到国家、地域限制，所支持的兑换货币能力也限制于地方政策法规。区块链构建的系统无边界，只需接入世界互联网即可使用（合约代码可以由任何人、任何机构编写，运行在整个区块网络上供任何人使用）。