Zcash是如何工作的？

在比特币和以太坊等知名加密货币中，交易被公开记录，并永久存储在区块链中。虽然区块链的去中心化提供了透明度，但也可能影响隐私。在中心化模型中，只要信任中央方，隐私就容易实现。在传统银行服务中，客户的交易保持机密，除非有法律理由要求披露。然而，同时实现去中心化和隐私可能会很具挑战性，因为交易必须对所有人可见，以进行适当的交易历史验证。

隐藏交易历史的一种方法是使用混合服务。混合服务接收来自多个用户的币，并将它们组合在一起，以模糊每个交易的目的地。然而，这也存在缺点：当用户较少时，维持隐私会很困难。此外，混合服务可以访问所有信息，并可能在恶意行为的情况下盗取币。

Zerocash↗是由Ben-Sasson等人提出的去中心化匿名支付方案，被认为是一种隐私币。它允许用户以去中心化的方式发送币，而不揭示目的地或金额，使用零知识证明。

在这篇文章中，我们将讨论Zerocash的结构及其在现实中的应用，特别是Zcash↗。

背景

在本节中，我们将介绍Zerocash的基础密码学协议，这些是其构建块。

承诺方案

承诺方案是一种密码协议，允许一方在不揭示其值的情况下承诺一个信息或值，随后以可验证的方式揭示其值。这在某些情况下是有用的，例如当一方需要证明他们在早些时候对某个信息做出了承诺，而直到以后才揭示该信息。

承诺方案可以使用密码哈希函数构建。为了承诺一个消息 mmm，只需揭示 com=h(r∣∣m)\text{com} = h(r || m)com=h(r∣∣m)，其中 rrr 是随机数，hhh 是密码哈希函数，而 ∣∣||∣∣ 表示连接操作。由于预图像抗性属性，无法从 com\text{com}com 恢复 mmm。我们将一个给定随机数 rrr 的消息 mmm 的承诺表示为 comr(m)\text{com}_r(m)comr​(m)。

伪随机函数

伪随机函数（PRF）是一个接受输入 xxx 并输出一个看起来随机的字符串的函数。PRF 以种子初始化，种子一般是公开的。它是确定性的，因此如果种子和 xxx 相同，输出始终相同。此外，如果 xxx 不可知，输出是不可预测的。

PRF 也可以从密码哈希函数构建。例如，PRFseed(x)=h(seed∣∣x)\text{PRF}_{\text{seed}}(x) = h(\text{seed} || x)PRFseed​(x)=h(seed∣∣x) 这是不可预测的。

零知识证明与 zk-SNARK

零知识证明是一种密码技术，允许证明者在不透露任何超出陈述真相的信息的情况下，向验证者证明一个陈述的真实性。这种技术使证明者能够向验证者展示他们对一个机密值的知识，而不泄露该值或任何相关细节。零知识证明必须满足三个属性：

1. 完备性。如果陈述是真的，那么诚实的证明者应该能够说服验证者承认其真实性。
2. 牢靠性。如果陈述是假的，那么没有欺骗的证明者应该无法说服验证者承认其真实性。
3. 零知识性。证明不应揭示超出陈述真实性的任何额外信息。

直观地说，证明者可以说服他们对 xxx 的知识，即 f(x)=yf(x) = yf(x)=y，而不向验证者揭示 xxx 本身。

zk-SNARK 是一种零知识证明协议，具有一种称为简洁性的附加特性（即，证明大小和验证者时间是亚线性的）。Zerocash 使用 zk-SNARK 进行零知识证明。即使不知道 zk-SNARK 是如何工作的，基于上述属性，仍然可以理解Zerocash的结构。因此，我们将省略进一步的细节。如果有兴趣，请查看我们博客中的零知识介绍：ZK 领域的导游，第 1 部分↗。

UTXO：比特币中的交易

为了更好地理解Zerocash协议，有必要首先检查比特币中的交易是如何运作的。在比特币中，每个用户持有的资产量是通过未花费的交易输出（UTXO）模型进行管理的。在典型的银行系统中，每个用户都有一个余额，余额的增加或减少取决于存款/取款。这个模型被称为账户模型。然而，在UTXO模型中，称为UTXO的单个单位的币在用户之间转移。

假设Alice和Bob分别从挖矿中获得6.25 BTC。然后每个挖矿结果都会记录在交易中。换句话说，Alice和Bob各自持有6.25 BTC UTXO。每个用户的UTXO列表如下：

• Alice : 6.25 BTC,
• Bob : 6.25 BTC.

他们希望向查尔斯发送1 BTC。那么，Alice的交易输入是她挖矿获得的6.25 BTC UTXO，而输出是1 BTC UTXO给查尔斯，5.25 BTC UTXO给Alice。她通过将剩余的币发送给自己来获取找零。现在，6.25 BTC 交易输出被使用，并创建了一个新的 5.25 BTC UTXO。Bob也是如此。每个用户的UTXO列表如下：

• Alice : 5.25 BTC,
• Bob : 5.25 BTC,
• 查尔斯 : 1 BTC, 1 BTC.

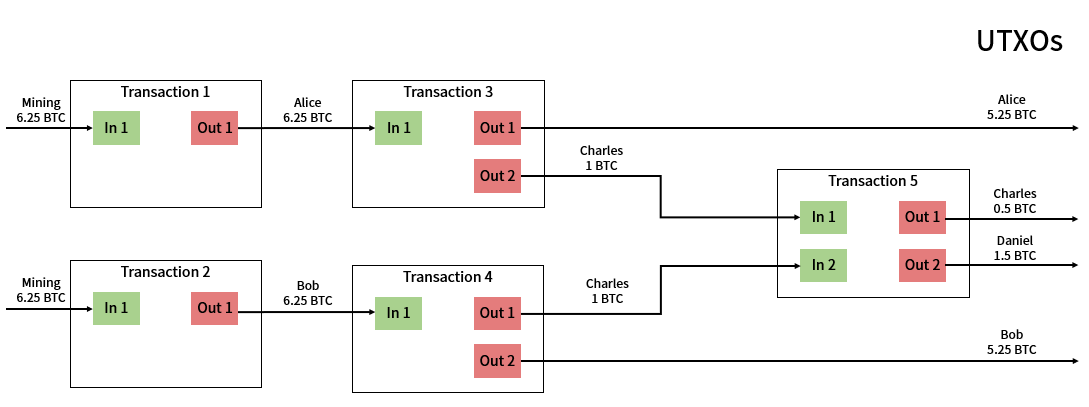交易示例的图形概述。

如果 1）UTXO 输入未被使用过，2）输入和输出的总和相等（为了简单起见，忽略交易手续费），3）交易由发送者生成，则交易被视为有效。前两个条件可以很容易地验证。要验证第三个条件，交易的数字签名会嵌入在交易中。如果 UTXO 输入属于多个所有者，那么就会嵌入多签名↗。

Zerocash 协议

Zerocash 协议中的交易基于比特币中的交易。为了澄清，由于Zerocash协议也使用UTXO模型，我们只需满足上述三个条件。然而，当目的地甚至金额被隐藏时，可能无法满足所有这些条件。例如，在不揭示金额的情况下，验证输入总和和输出总和是否相等似乎是奇怪的。然而，通过使用零知识证明可以实现这一点。

正如提到的，证明者可以说服验证者他们对 xxx 的知识，即 f(x)=yf(x) = yf(x)=y，而不向验证者揭示 xxx 本身。因此，一旦我们将交易的所有条件表示为方程，发送者就可以证明其交易的有效性，揭示敏感信息。我们将讨论如何将条件设置为方程。下面的简化将为我们提供协议的更大图景，然后我们将分解以了解Zerocash交易的细节。

协议（简化）

这是在Zerocash论文中引入的Zerocash协议的简化版本。在此协议中，币的值是固定的。如果Alice想要铸造一个新币 ccc，Alice做如下操作：

1. Alice采样一个随机的序列号 snsnsn 和一个陷门 rrr，计算币承诺 cm=comr(sn)cm = \text{com}_r(sn)cm=comr​(sn)。现在定义一个新币 c:=(r,sn,cm)c := (r,sn,cm)c:=(r,sn,cm)。
2. 将包含 cmcmcm 的相应铸造交易 txMint\text{tx}_\text{Mint}txMint​ 发送到分类账中。注意 snsnsn 与 rrr 都不会被发送。

如果Alice想花费 ccc，Alice执行如下操作：

1. Alice发布包含币的序列号 snsnsn 和她对 rrr 的知识的 zk-SNARK 证明 π\piπ 的交易 txSpend\text{tx}_\text{Spend}txSpend​，使得 comr(sn)\text{com}_r(sn)comr​(sn) 显示在币承诺列表中。如果 snsnsn 在过去的支出交易中未出现，则交易有效。

通过在Merkle 树↗中维护币承诺列表，能够高效地进行会员检查，同时通过 zk-SNARK 的零知识性保证隐私。用户可以证明他们对 rrr 的知识，而不透露与列表中 comr(sn)\text{com}_r(sn)comr​(sn) 相对应的哪个币。

协议（准确）

虽然简化版本有助于理解Zerocash的基本概念，但存在多个限制。首先，假设一个币对应一美元，如果用户想要转移100美元，他们必须发布100个交易，这是不有效率且泄露金额。其次，转移一个币并不自然定义。在这个过程中，Alice可以证明币 ccc 是由她自己铸造的。然而，如果Alice希望将 ccc 转移给Bob，唯一可能的方法是通知Bob rrr 和 snsnsn。在这种情况下，Alice可能在Bob之前先支出 ccc，即使她不这样做，如果Bob支出 ccc，Alice将在交易中检查 snsnsn 时得知。

确切的协议包含多种方法来防止这些缺陷。让我们来看看该协议。

在完整协议中，每个用户生成地址。通常，地址是一个密钥对 (apk,ask)(a_{pk}, a_{sk})(apk​,ask​)，其中 apka_{pk}apk​ 是公钥， aska_{sk}ask​ 是私钥。密钥对的生成是通过随机采样 aska_{sk}ask​，然后设定 apk:=PRFask(0)a_{pk} := \text{PRF}_{a_{sk}}(0)apk​:=PRFask​​(0)。用户可以生成任意数量的地址密钥对。

铸造

为了铸造一个价值为 vvv 的新币 ccc，Alice遵循以下步骤：

1. Alice采样 ρ\rhoρ，然后计算币的序列号 sn:=PRFask(ρ)sn := \text{PRF}_{a_{sk}}(\rho)sn:=PRFask​​(ρ)。
2. Alice计算 k:=comr(apk∣∣ρ)k := \text{com}_r(a_{pk} || \rho)k:=comr​(apk​∣∣ρ) 对于随机数 rrr，然后计算 cm:=coms(v∣∣k)cm := \text{com}_s(v || k)cm:=coms​(v∣∣k) 对于随机数 sss。
3. 生成一个币 c:=(apk,v,ρ,r,s,cm)c := (a_{pk}, v, \rho, r, s, cm)c:=(apk​,v,ρ,r,s,cm) 和铸造交易 txMint:=(v,k,s,cm)\text{tx}_{\text{Mint}} := (v, k, s, cm)txMint​:=(v,k,s,cm)。

与简化协议相比，交易中包含了用户的公钥地址。此外，承诺过程变得更加复杂。这种嵌套结构使任何人都能够通过检查 cm=coms(v∣∣k)cm = \text{com}_s(v || k)cm=coms​(v∣∣k)，而不需要 zk-SNARK 证明来验证 cmcmcm 是某个币值 vvv 的承诺，同时保持所有者和序列号的隐秘。

倾倒

币的支出通过倾倒操作进行，该操作类似于UTXO模型。该操作采用一组输入币进行消耗，并将其值倾倒至一组新的输出币中。

Alice使用她的地址密钥对 (apk,ask)(a_{pk}, a_{sk})(apk​,ask​) 消耗她的币：

cold:=(apkold,vold,ρold,rold,sold,cmold)c^{\text{old}} := (a_{pk}^{\text{old}}, v^{\text{old}}, \rho^{\text{old}}, r^{\text{old}}, s^{\text{old}}, cm^{\text{old}})cold:=(apkold​,vold,ρold,rold,sold,cmold)

并生成两个新币：

c1new:=(apk,1new,v1new,ρ1new,r1new,s1new,cm1new)c_1^{\text{new}} := (a_{pk,1}^{\text{new}}, v_1^{\text{new}}, \rho_1^{\text{new}}, r_1^{\text{new}}, s_1^{\text{new}}, cm_1^{\text{new}})c1new​:=(apk,1new​,v1new​,ρ1new​,r1new​,s1new​,cm1new​) 和 c2new:=(apk,2new,v2new,ρ2new,r2new,s2new,cm2new)c_2^{\text{new}} := (a_{pk,2}^{\text{new}}, v_2^{\text{new}}, \rho_2^{\text{new}}, r_2^{\text{new}}, s_2^{\text{new}}, cm_2^{\text{new}})c2new​:=(apk,2new​,v2new​,ρ2new​,r2new​,s2new​,cm2new​)

程序如下。

1. Alice为 i∈{1,2}i \in \{1,2\}i∈{1,2} 采样 ρinew\rho_i^{\text{new}}ρinew​。
2. Alice计算 kinew:=comrinew(apk,inew∣∣ρinew)k_i^{\text{new}} := \text{com}_{r_i^{\text{new}}}(a_{pk,i}^{\text{new}} || \rho_i^{\text{new}})kinew​:=comrinew​​(apk,inew​∣∣ρinew​) 对于随机 rinewr^{\text{new}}_irinew​，其中 i∈{1,2}i \in \{1,2\}i∈{1,2}。
3. Alice计算 cminew:=comsinew(vinew∣∣kinew)cm_i^{\text{new}} := \text{com}_{s_i^{\text{new}}}(v_i^{\text{new}} || k_i^{\text{new}})cminew​:=comsinew​​(vinew​∣∣kinew​) 对于随机 sinews_i^{\text{new}}sinew​，其中 i∈{1,2}i \in \{1,2\}i∈{1,2}。
4. 现在生成两个新币 c1new:=(apk,1new,v1new,ρ1new,r1new,s1new,cm1new)c_1^{\text{new}} := (a_{pk,1}^{\text{new}}, v_1^{\text{new}}, \rho_1^{\text{new}}, r_1^{\text{new}}, s_1^{\text{new}}, cm_1^{\text{new}})c1new​:=(apk,1new​,v1new​,ρ1new​,r1new​,s1new​,cm1new​) 和 c2new:=(apk,2new,v2new,ρ2new,r2new,s2new,cm2new)c_2^{\text{new}} := (a_{pk,2}^{\text{new}}, v_2^{\text{new}}, \rho_2^{\text{new}}, r_2^{\text{new}}, s_2^{\text{new}}, cm_2^{\text{new}})c2new​:=(apk,2new​,v2new​,ρ2new​,r2new​,s2new​,cm2new​) 被生成。Alice生成她对的 zk-SNARK 证明 πPour\pi_{\text{Pour}}πPour​，以证明她对 cold,c1new,c2newc^{\text{old}}, c_1^{\text{new}}, c_2^{\text{new}}cold,c1new​,c2new​ 和 askolda_{sk}^{\text{old}}askold​ 的知识，使得
   • 这些币是形成良好的： kold=comrold(apkold)k^{\text{old}}=\text{com}_{r^{\text{old}}}(a_{pk}^{\text{old}})kold=comrold​(apkold​)， k1new=comr1new(apk,1new)k_1^{\text{new}}=\text{com}_{r_1^{\text{new}}}(a_{pk,1}^{\text{new}})k1new​=comr1new​​(apk,1new​)， k2new=comr2new(apk,2new)k_2^{\text{new}}=\text{com}_{r_2^{\text{new}}}(a_{pk,2}^{\text{new}})k2new​=comr2new​​(apk,2new​)， cmold=comsold(vold∣∣kold)cm^{\text{old}} = \text{com}_{s^{\text{old}}}(v^{\text{old}} || k^{\text{old}})cmold=comsold​(vold∣∣kold)， cm1new=coms1new(v1new∣∣k1new)cm_1^{\text{new}} = \text{com}_{s_1^{\text{new}}}(v_1^{\text{new}} || k_1^{\text{new}})cm1new​=coms1new​​(v1new​∣∣k1new​)，和 cm2new=coms2new(v2new∣∣k2new)cm_2^{\text{new}} = \text{com}_{s_2^{\text{new}}}(v_2^{\text{new}} || k_2^{\text{new}})cm2new​=coms2new​​(v2new​∣∣k2new​)。
   • 地址私钥与公钥匹配： apkold=PRFaskold(0)a_{pk}^{\text{old}} = \text{PRF}_{a_{sk}^{\text{old}}}(0)apkold​=PRFaskold​​(0)。
   • 序列号正确计算： snold:=PRFaskold(ρold).sn^{\text{old}} := \text{PRF}_{a_{sk}^{\text{old}}}(\rho^{\text{old}}).snold:=PRFaskold​​(ρold)。
   • 币承诺 cmoldcm^{\text{old}}cmold 出现在币承诺列表中。
   • 值相加： v1new+v2new=voldv_1^{\text{new}} + v_2^{\text{new}} = v^{\text{old}}v1new​+v2new​=vold。
5. 将生成的倾倒交易 txPour:=(snold,cm1new,cm2new,πPour)\text{tx}_{\text{Pour}} := (sn^{\text{old}}, \text{cm}_1^{\text{new}}, \text{cm}_2^{\text{new}}, \pi_{\text{Pour}})txPour​:=(snold,cm1new​,cm2new​,πPour​) 附加到分类账中。如果 snoldsn^{\text{old}}snold 在过去的倾倒交易中未出现，则交易有效。

下面的插图介绍了币承诺的结构。

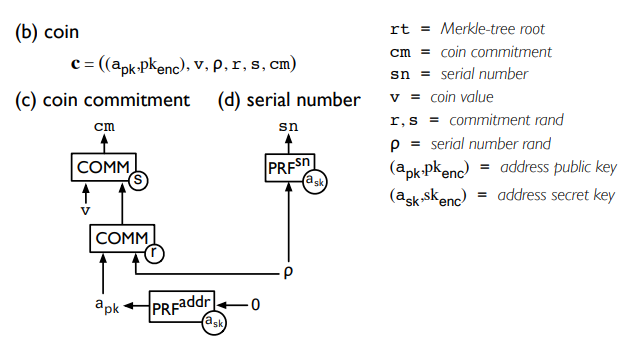币承诺结构的插图。 pkencpk_{enc}pkenc​ 指的是点 1 中提到的公钥密码系统中的接收者公钥。图片来源于Zerocash论文。

zk-SNARK πPour\pi_{\text{Pour}}πPour​ 所证明的声明相当复杂。建议仔细检查每个声明。为了帮助读者理解，以下是一些要点：

1. 如果Alice想将 c1newc_1^\text{new}c1new​ 发送给Bob，她首先需要知道Bob的地址公钥，并将 apk,1newa_{pk,1}^{\text{new}}apk,1new​ 设置为Bob的地址公钥。此外，她还需要提供 (v1new,ρ1new,r1new,s1new)(v_1^\text{new}, \rho_1^\text{new}, r_1^\text{new}, s_1^\text{new})(v1new​,ρ1new​,r1new​,s1new​)。这些可以通过私密信道传递，或事先准备公钥密码系统并将密文 Enc(v1new,ρ1new,r1new,s1new)\text{Enc}(v_1^\text{new}, \rho_1^\text{new}, r_1^\text{new}, s_1^\text{new})Enc(v1new​,ρ1new​,r1new​,s1new​) 以Bob的公钥进行添加。
2. 假设 (v1new,ρ1new,r1new,s1new)(v_1^\text{new}, \rho_1^\text{new}, r_1^\text{new}, s_1^\text{new})(v1new​,ρ1new​,r1new​,s1new​) 是通过公钥密码系统提供的。那么，为了接收一个币，Bob应该验证整个倾倒交易，以便让 Enc(v1new,ρ1new,r1new,s1new)\text{Enc}(v_1^\text{new}, \rho_1^\text{new}, r_1^\text{new}, s_1^\text{new})Enc(v1new​,ρ1new​,r1new​,s1new​) 用Bob自己的私钥进行解密。
3. 如果Alice不知道 ask,1newa_{sk,1}^{\text{new}}ask,1new​，那么Alice就无法生成有效的 πPour\pi_{\text{Pour}}πPour​ 用于支出 c1newc_1^{\text{new}}c1new​。特别是，这与第二个声明，即_地址私钥与公钥匹配_矛盾。
4. 假设 c1newc_1^\text{new}c1new​ 属于Bob。当Bob支出 c1newc_1^{\text{new}}c1new​ 时，Alice无法找到它，因为 sn1new=PRFask,1new(ρ1new)sn_1^{\text{new}} = \text{PRF}_{a_{sk,1}^\text{new}}(\rho_1^{\text{new}})sn1new​=PRFask,1new​​(ρ1new​) 在交易中被揭示，但Alice并不知道它。

现在我们了解了协议，让我们检查Zerocash的现实实施：Zcash。

Zcash：Zerocash的实现

Zcash↗ 是 Zerocash 的一个实现。Zerocash 在 2014 年发布，Zcash 于 2016 年推出。从那时起，它经历了持续的发展。本质上，Zcash 遵循了Zerocash中介绍的方法，但在过去十年中进行了一些更改。它从初始的概念证明实现演变为市场价值约达四亿美金的庞大生态系统。

Zcash 提供两种类型的地址：z 地址和 t 地址。t 地址之间的交易是透明的，类似于比特币交易。z 地址之间的交易是隐蔽的，类似于 Zerocash 交易。也可以从 t 地址发送币到 z 地址，或从 z 地址发送币到 t 地址。在这两种情况下，只有 t 地址一侧的值被揭示。

Zcash 有三种隐蔽协议，分别是Sprout、Sapling和Orchard。Sprout 是在 Zcash 启动时实现的原始协议。Sapling 于 2018 年推出，解决了 Sprout 协议的局限，并提供了更快的交易生成和验证。Orchard 是最新的协议升级，于 2022 年激活，进一步增强了隐私和可扩展性。Orchard 使用了一种新的 zk-SNARK，称为 Halo2↗，这 eliminates 了对被信任的设置的需求。这是对 Sprout 中的 BCTV14↗ 以及在 Sapling 中的 Groth16↗ 的改进。目前，Sapling 是使用最广泛的隐蔽协议。

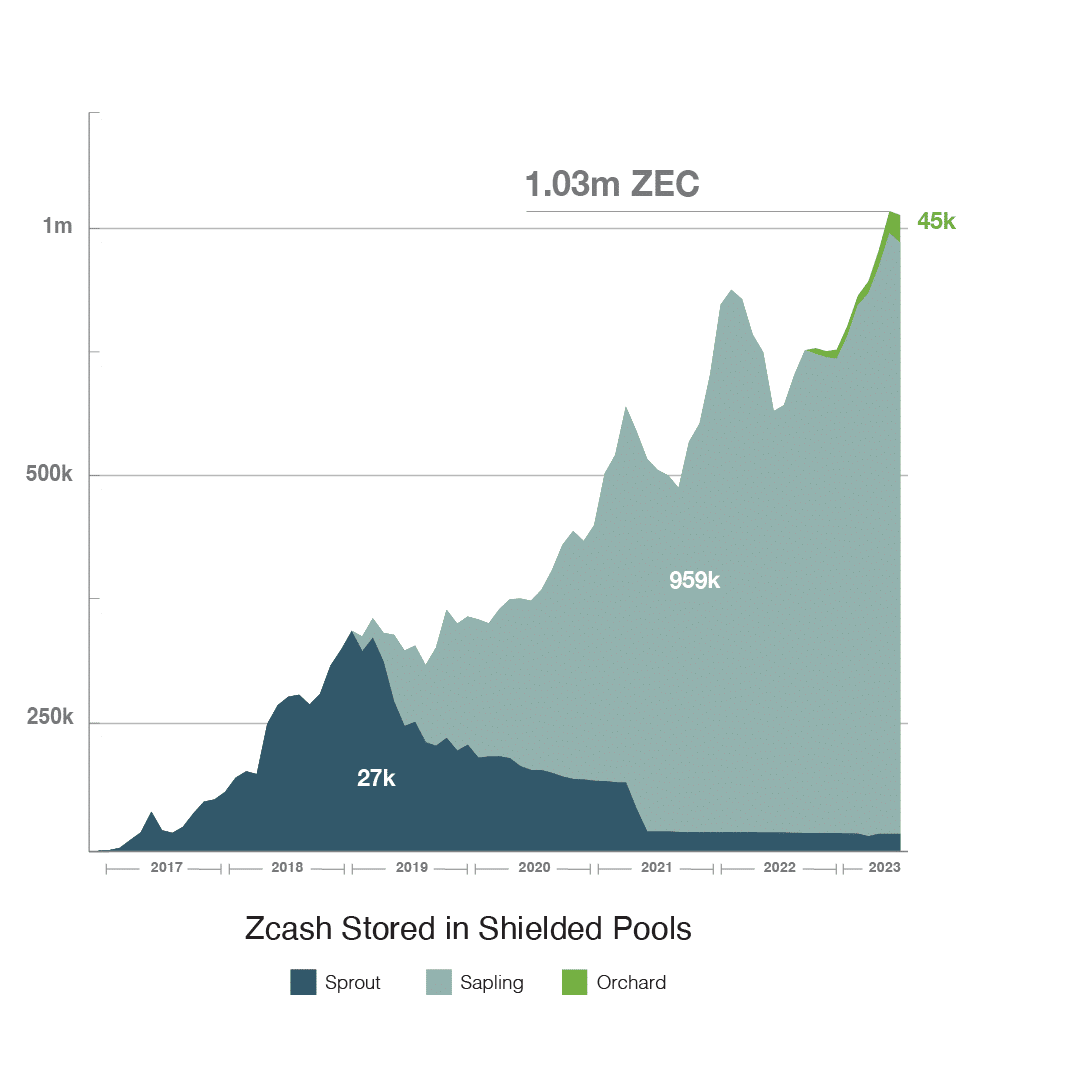自 2016 年以来 Zcash 三个隐蔽池中存储的 ZEC 数量。图片来自 ELECTRIC COIN CO.↗

有关协议结构的更多信息，请参阅 Zcash 协议规范↗。

对 Zcash 的攻击

有些情况下发现了 Zcash 协议中的密码学漏洞，并对协议进行了修改。我们将讨论 Faerie Gold 攻击和内部哈希碰撞攻击，这些也在协议规范中提到。请注意，这些漏洞已经被开发者解决。

Faerie Gold攻击

在Zerocash协议中，币的序列号通过 sn=PRFask(ρ)sn = \text{PRF}_{a_{sk}}(\rho)sn=PRFask​​(ρ) 与任意选择的 ρ\rhoρ 确定。如果Alice需要向Bob发送两个币 c1c_1c1​ 和 c2c_2c2​，却想做些恶意的事情，那么她可能为 c1c_1c1​ 和 c2c_2c2​ 选择相同的 ρ\rhoρ。然后序列号 sn1sn_1sn1​ 和 sn2sn_2sn2​ 碰撞。尽管两个币都是有效的，但Bob只能使用其中一个，因为交易中的序列号会被检查以查看是否已经出现过。

为了应对这个问题，Zcash通过修改规范确保ρ\rhoρ 的唯一性。取而代之的是随机选择 ρ\rhoρ，它是从 PRF 派生出来的。PRF 的输入是每笔交易中不同的哈希摘要 hSigh_{\text{Sig}}hSig​，以及输出顺序索引 iii。如果 c1c_1c1​ 和 c2c_2c2​ 在不同的交易中生成，那么 hSigh_{\text{Sig}}hSig​ 值会不同，如果它们在同一笔交易中生成，则输出顺序索引 iii 会不同。因此 ρ\rhoρ 永远不会碰撞。

内部哈希碰撞攻击

回顾铸造一个新币 ccc 的过程，其值为 vvv，Zerocash 中的步骤为：

1. Alice采样 ρ\rhoρ，然后计算币的序列号 sn:=PRFask(ρ)sn := \text{PRF}_{a_{sk}}(\rho)sn:=PRFask​​(ρ)。
2. Alice计算 k:=comr(apk∣∣ρ)k := \text{com}_r(a_{pk} || \rho)k:=comr​(apk​∣∣ρ) 对于随机 rrr，然后计算 cm:=coms(v∣∣k)cm := \text{com}_s(v || k)cm:=coms​(v∣∣k) 对于随机 sss。
3. 生成一个币 c:=(apk,v,ρ,r,s,cm)c := (a_{pk}, v, \rho, r, s, cm)c:=(apk​,v,ρ,r,s,cm) 和铸造交易 txMint:=(v,k,s,cm)\text{tx}_{\text{Mint}} := (v, k, s, cm)txMint​:=(v,k,s,cm)。

在原始Zcash设计中，承诺 cmcmcm 的派生如下：

1. InternalH=SHA256(apk∣∣ρ) 截取为 128 位InternalH = \text{SHA256}(a_{pk} || \rho) \text{ 截取为 128 位}InternalH=SHA256(apk​∣∣ρ) 截取为 128 位
2. k=SHA256(r∣∣InternalH)k = \text{SHA256}(r || InternalH)k=SHA256(r∣∣InternalH)
3. cm=SHA256(k∣∣0192∣∣v)cm = \text{SHA256}(k || 0^{192} || v)cm=SHA256(k∣∣0192∣∣v)

由于 InternalHInternalHInternalH 仅为 128 位，攻击者可以发现 (apk,ρ)(a_{pk}, \rho)(apk​,ρ) 和 (apk′,ρ′)(a_{pk}', \rho')(apk′​,ρ′) 具有相同的 InternalHInternalHInternalH，计算量为 O(264)O(2^{64})O(264)。派生自 (apk,ρ)(a_{pk}, \rho)(apk​,ρ) 和 (apk′,ρ′)(a_{pk}', \rho')(apk′​,ρ′) 的两个币 看起来不同，因为它们的序列号 PRFask(ρ)\text{PRF}_{a_{sk}}(\rho)PRFask​​(ρ) 和 PRFask′(ρ′)\text{PRF}_{a_{sk}'}(\rho')PRFask′​​(ρ′) 是不同的。因此，攻击者可以通过使用 (apk,ρ)(a_{pk}, \rho)(apk​,ρ) 和 (apk′,ρ′)(a_{pk}', \rho')(apk′​,ρ′) 生成两个不同的 zk-SNARK 证明来进行双重支付。

为了解决这个问题，承诺被更改为 cm=SHA256(0xB0∣∣apk∣∣v∣∣ρ∣∣r)cm = \text{SHA256}(\text{0xB0} || a_{pk} || v || \rho || r)cm=SHA256(0xB0∣∣apk​∣∣v∣∣ρ∣∣r)。通过此修正，Zcash 同时承诺了 apk,v,ρa_{pk}, v, \rhoapk​,v,ρ 和 rrr，而 Zerocash 使用的是一种嵌套的承诺方案，其中 apka_{pk}apk​ 和 kkk 首先被承诺，然后是 vvv。Zerocash 中嵌套承诺方案的原因是允许铸造交易在不需要 zk-SNARK 证明的情况下公开验证。然而，在 Zcash 中，铸造和倾倒交易相结合，并且每次传输始终使用 zk-SNARK 证明。因此，Zcash 不需要嵌套。

结论

本文讨论了 Zerocash 及其在 Zcash 中的使用，Zcash是一种加密货币。Zerocash 是一个增强加密货币隐私和匿名性的协议，解决了安全和隐私问题。它使用先进的加密技术，例如 zk-SNARKs，在隐蔽发送者、接收者和交易金额的同时证明交易的有效性。此功能使用户能够保留区块链的透明性和完整性，同时隐蔽其交易内容。此外，从研究者的角度看，深入调查此协议以识别潜在漏洞，例如 Faerie Gold 攻击，也是很有趣的。

关于我们

Zellic 专注于保护新兴技术。我们的安全研究人员在最有价值的目标中发现了漏洞，从财富500强公司到 DeFi 巨头。

开发者、创始人和投资者信任我们的安全评估能够迅速、安心且无重大漏洞地交付产品。凭借我们在现实世界攻防安全研究方面的背景，我们发现了其他人所遗漏的东西。

联系我们↗，获取更优质的审计服务。真实审计，而非例行公事。

• 原文链接： zellic.io/blog/how-does-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～