PCS: Binius 解析

PCS: Binius 解释

本文将介绍由 Irreducible (原 Ulvetanna) 所提出的 binary field 中建立 SNARK 的方法 Binius。

Photo by <a href="https://unsplash.com/@eva_gorobets_?utm_content=creditCopyText&utm_medium=referral&utm_source=unsplash">Eva Gorobets</a> on <a href="https://unsplash.com/photos/gray-and-black-textile-on-white-surface-vJ4NYVIhQpU?utm_content=creditCopyText&utm_medium=referral&utm_source=unsplash">Unsplash&lt;/a>

目录

• 简介
• PCS 的简单回顾
• Binary Tower
• Reed-Solomon 耗损码
• Kronecker 乘积
• Vitalik 的 Binius 示例
• 总结
• 参考文献

引言

传统的 SNARK 通常会在 256 位元以上的有限体中做运算，为了在这么大的有限体中做运算，电路中的数字就必须用这么多的空间来储存，你可以想象在你的电路当中有一堆 1 占用了 256 位元会有多浪费空间。

那么既然在那么大的有限体中运算很耗资源，我们为什么不将有限体缩小，缩小到极致，也就是只剩下 0 跟 1 的 binary field（GF(2)）。而 Binius 就是在 binary field 中运算的 SNARK，更准确的来说，Binius 是在 binary field 中的 polynomial commitment scheme。

PCS 的简单回顾

现代组成 SNARK 的方式是把 IOP (Interactive oracle proof) 和 PCS (Polynomial commitment scheme) 结合在一起，其中我要讲的是 polynomial commitment。

Polynomial commitment 是一个可以代表多项式的表示方法。Prover 可以将一个多项式 commit 成一个 polynomial commitment，并在之后向 verifier 证明这个多项式上的某个点的值，而不用公开整个多项式。

而证明的方式会使用高中学过的余式定理，如果我要证明 $P(z) = a$，那我只需要证明 $\frac{P(x)-a}{x-z}$ 是一个多项式就好了。原因如下，如果 $P(z) = a$，那么根据余式定理就满足 $P(z)=(x-z)\cdot q(x)+a$，经过一番移项会得到 $\frac{P(z)-a}{x-z}=q(x)$，也就是以上所说的 $\frac{P(x)-a}{x-z}$ 是一个多项式。

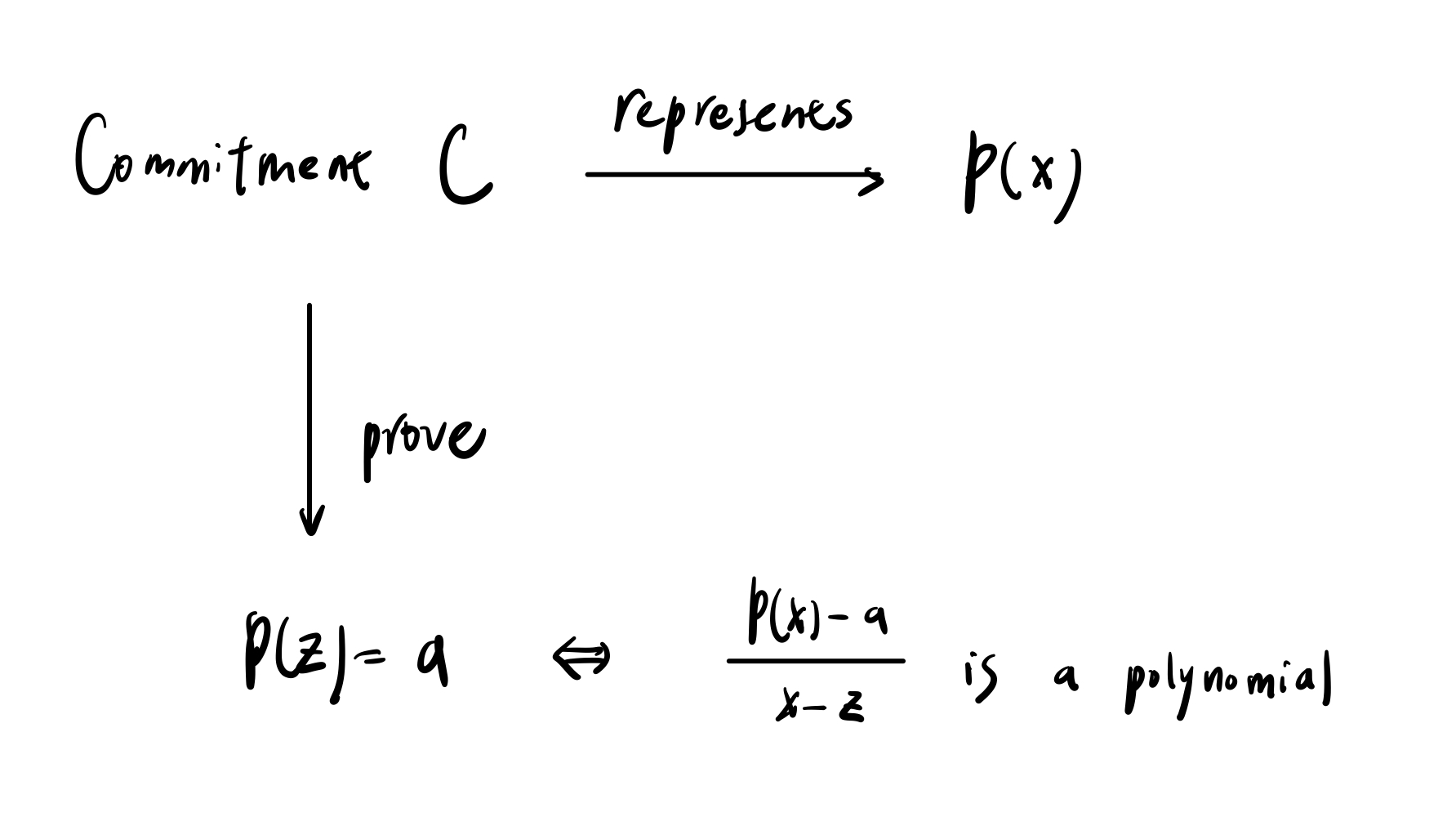
简单回顾一下 KZG commitment。

KZG 的第一个步骤是 trusted setup，由一个或多个完成。先取一个秘密 $s$，（这个秘密 $s$ 在完成 trusted setup 之后要被丢弃），以及两个椭圆曲线的 Generator $G_1$ 和 $G_2$，创造出两组序列 $[G_1, G_1\cdot s, G_1\cdot s^2, ..., G_1 \cdot s^n]$、$[G_2, G_2\cdot s, G_2\cdot s^2, ..., G_2 \cdot s^n]$，这些数字被称为 proving keys。

第二个步骤是 commit。Prover 将多项式 $P$ 转换成 commitment，方法是将原多项式的 $x^n$ 以 $G_1\cdot s^n$ 代换掉。我们用 $[P]$ 来代表 $P$ 的 commitment。

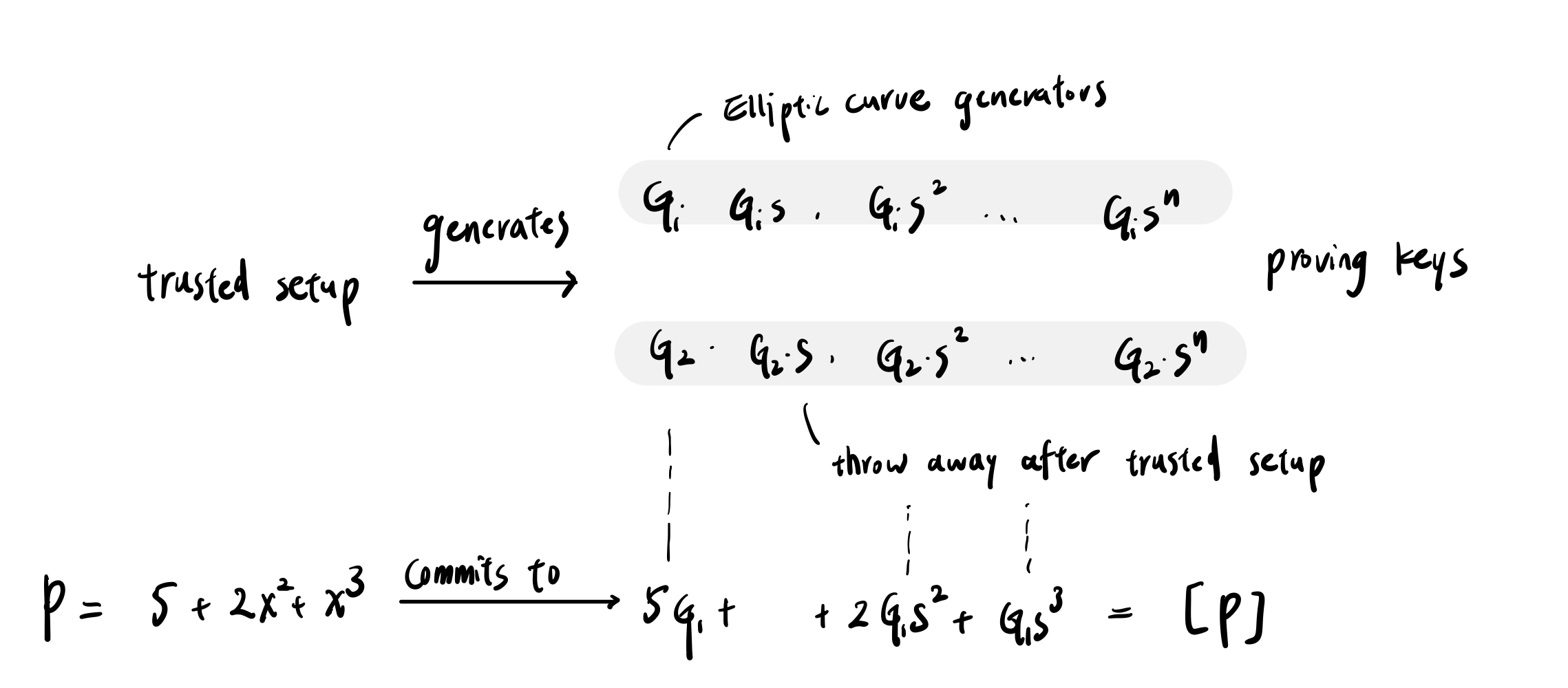
最后一步是证明，Verifier 只要确认两组椭圆曲线上的 Pairing 相等，就能被说服 $P(z)=a$。

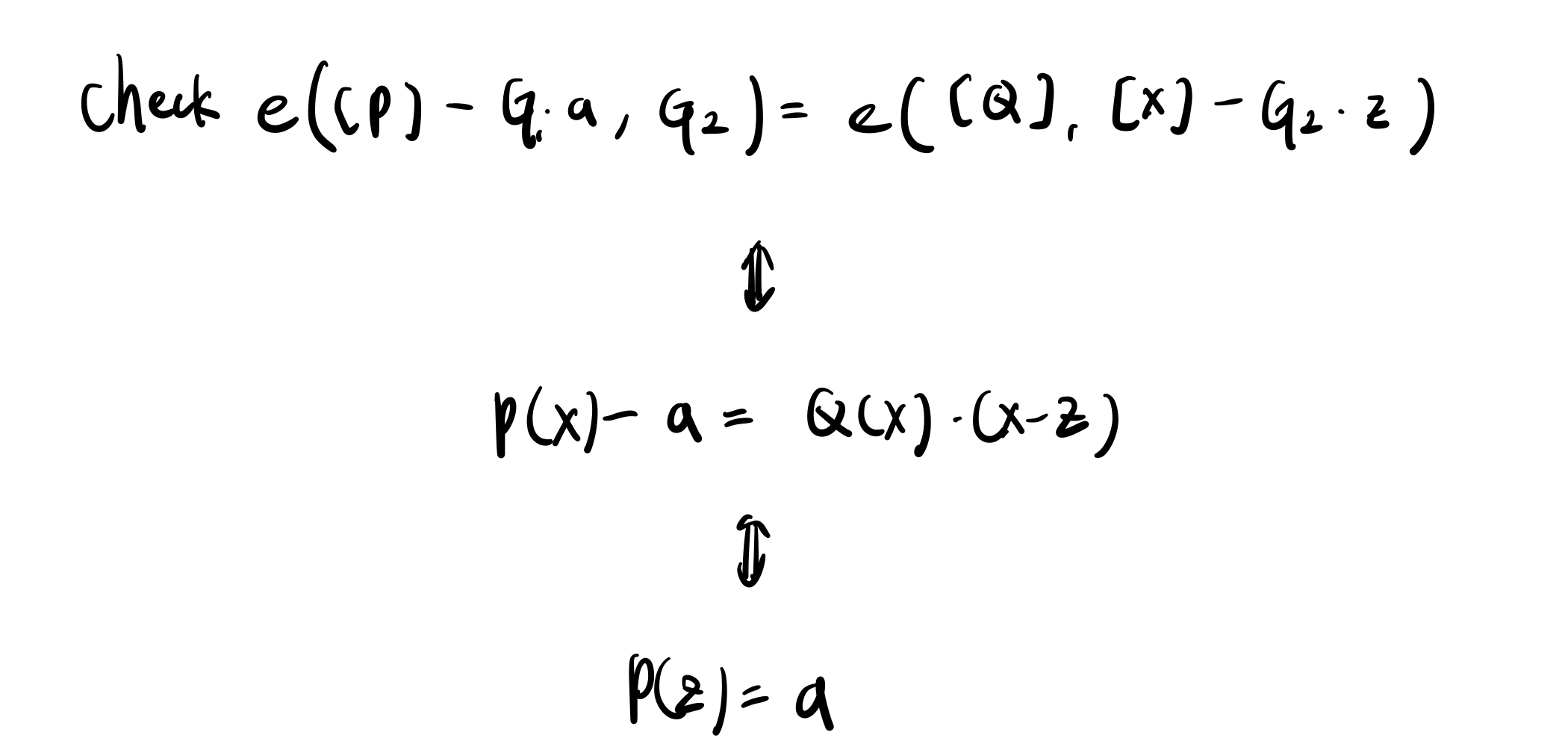
由于 KZG 并不是本文重点，所以就不多做背后数学逻辑的解释，读者只需要知道 Polynomial commitment 的用途即可。

Binary Tower

这部分会碰到比较难懂的抽象代数，而 Binius 又在这之上进行了改良，由最基本由 0 和 1 组成的 binary field（Galois Field $GF(2)$），进一步延伸出 $GF(2^n)$。

最传统的 $GF(2^n)$ 使用的是单变量的多项式运算，而为了加速运算，Binius 将单变量运算改成了多变量运算，变成了所谓的 binary tower （出自An iterated quadratic extension of GF(2) by Weidemann(1986)）。

我们会从最基本的 binary field 开始介绍，我相信这样会更容易理解 binary tower 在做什么。

binary field

有限体（域） Finite Fields，又称 Galois Fields，时常简写为 $GF(p)$，代表的是一个由 $1$ 到 $p-1$ 所组成的集合，所有在这个有限体中的运算都要 $mod\ p$。在这里需要注意的是 Galois Field 的 $p$ 必须是质数或是质数的某个次方。举个例子来说，$GF(7)$ 由 $Z_7 = {0,1,2,...,6}$ 组成，其中所有的运算都要除以 $7$ 取余数，也就限制了所有运算的结果最终都会回到这个集合内。

Binary Field，也就是 $GF(2)$，只由两个元素 ${0,1}$ 组成，所有运算的结果都是 0 或 1，我们可以将所有运算写在下表，左边是加法，右边是乘法：

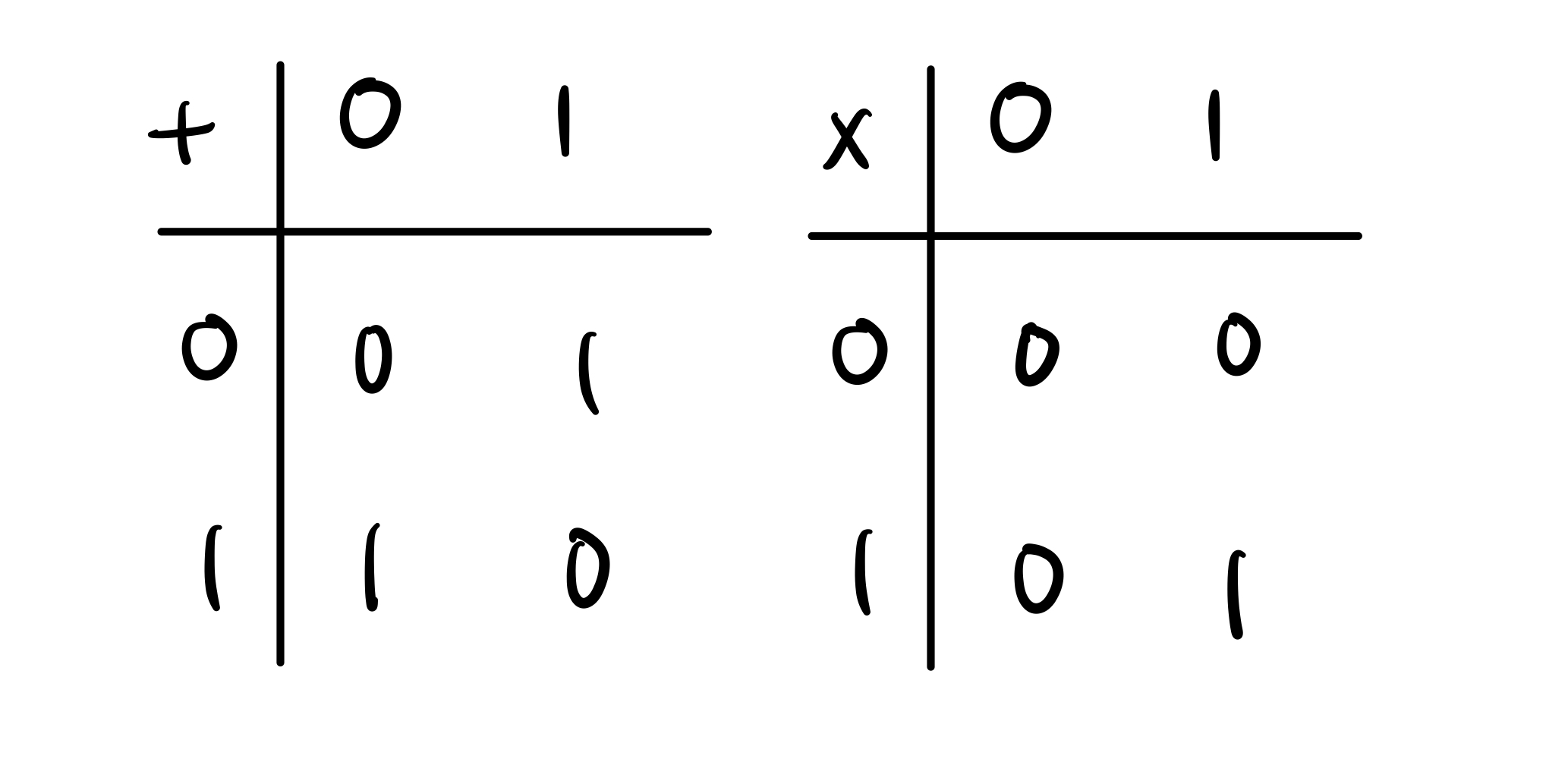
你可以发现在 binary field 中的加法就是 XOR，更方便的事情是减法就是加法。我们会想要在所有运算中拥有这些优点，这会让运算速度非常快。

那么如果我们今天想要处理 3 个 bit 的运算时，也就是我想要在 $Z_8 = {0,1,2,3,...,7}$ 中做运算时会发生什么问题（这里不能写 $GF(8)$ 因为 $p$ 必须是质数）。

如果你像上面一样把整个加法表跟乘法表写出来，你会发现在加法表里面没什么问题，在乘法表里面就会出问题了。在乘法表中，所有数字的出现频率是不一样的，也就是说如果你的加密系统建立在这样“有限体”中（当然它不能被称为有限体），攻击者有很高的概率可以利用频率分析来破解。第二个问题是，在这样的“有限体”当中，某些元素不存在乘法反元素，也就是不能进行除法。

为了解决这样结构的缺陷，又想要保留加法跟减法都是 XOR 的优点，我们需要介绍 $GF(2)$ 的扩展域 $GF(2^n)$。

extension field

$GF(2^n)$ 是 $GF(2)$ 的扩展域，包含 $2^n$ 个元素，每个元素可以用长度为 n 的二进制数表示。举个例子：$GF(2^3)$，由 ${000,001,010,011,100,101,110,111}$ 组成，你会想说这跟原本的有限体差在哪，不就是把原本的数字转成二进制表示法。其实不太一样，在这里我会建议大家先不要把它看成是一个二进制表示法，111 就是 111，不要想成 7（虽然后面我们还是会这么做），因为每一个位元代表的是一个多项式的系数。加法跟乘法都不是原先想象的加法跟乘法，且运算仍然是二进制的。

先跳到结论，这样的构建可以让乘法表中的每个数字出现频率相等、每个元素都有对应的乘法反元素、并且加法等同于减法。

在这样的有限体当中，每一个元素都被看成是一个多项式，其中每个位元代表的是 $x$ 的某个次方的系数。这有点像是小时候刚学多项式的除法时，我们为了简化只会写多项式的系数一样。所以在 $GF(2^3)$ 中的元素，其实是如下表所示的多项式。

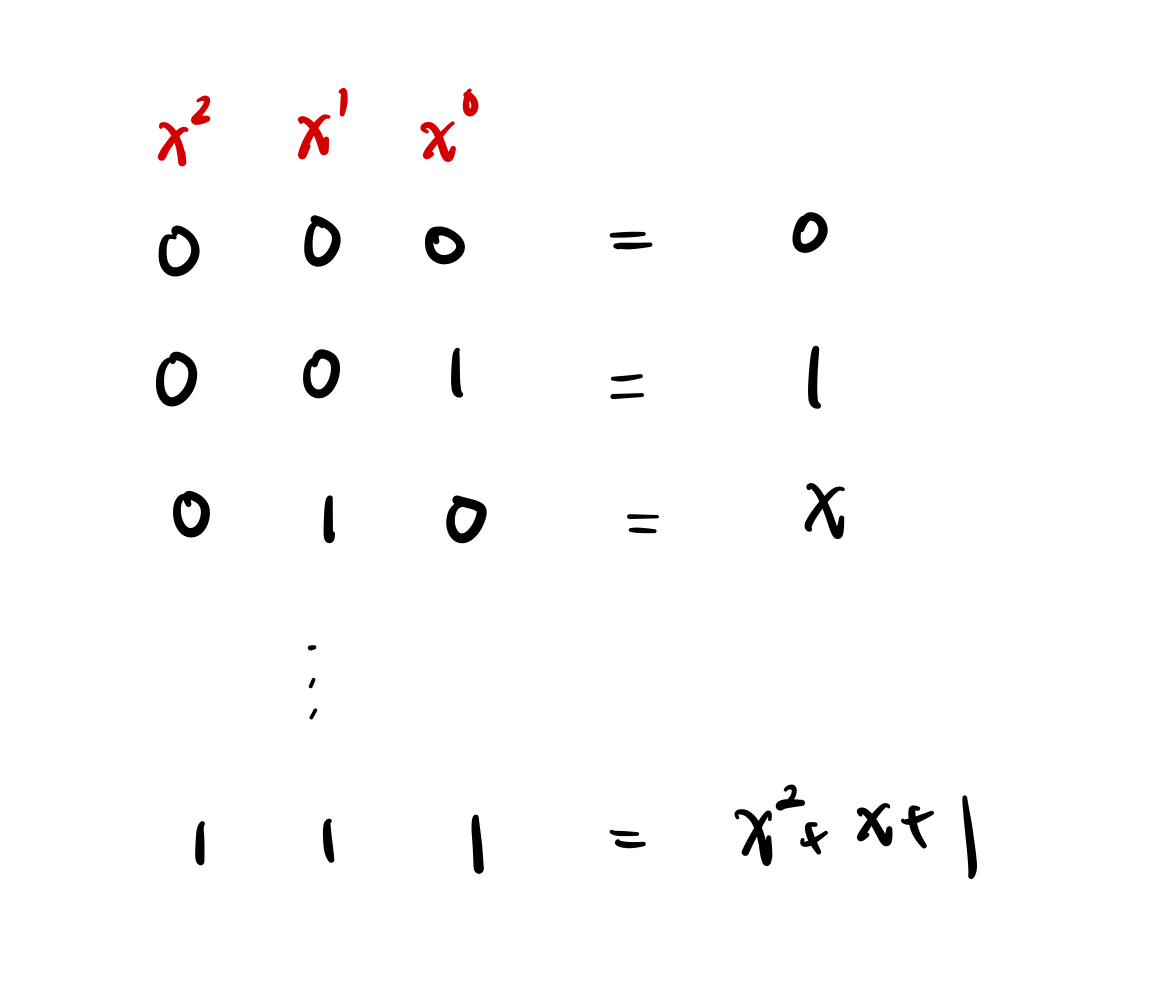
写成这样之后就好解释了，只要把两个数字都变成多项式，再进行加法跟减法，并且记得使用二进制，运算结果再变回系数表示法，所有的运算都将变得非常合理。

加法的部分比较简单，我举了个例子如下。应该不难看出，加法的结论就是 XOR。 $$\begin{aligned} 111+101 &= (x^2+x+1)+(x^2+1) \ &= 2x^2+x+2 \ &=x \ &= 010 \end{aligned}$$

乘法的部分比较复杂一点点，但只要带入不可约多项式（Irreducible polynomial）的概念，所有问题都将迎刃而解。不可约多项式其实就是在这个有限体中的模数。在原本的有限体中我们 mod p，而在扩展域中我们就 mod 不可约多项式。在这个例子当中，$x^3+x+1$ 就是不可约多项式。

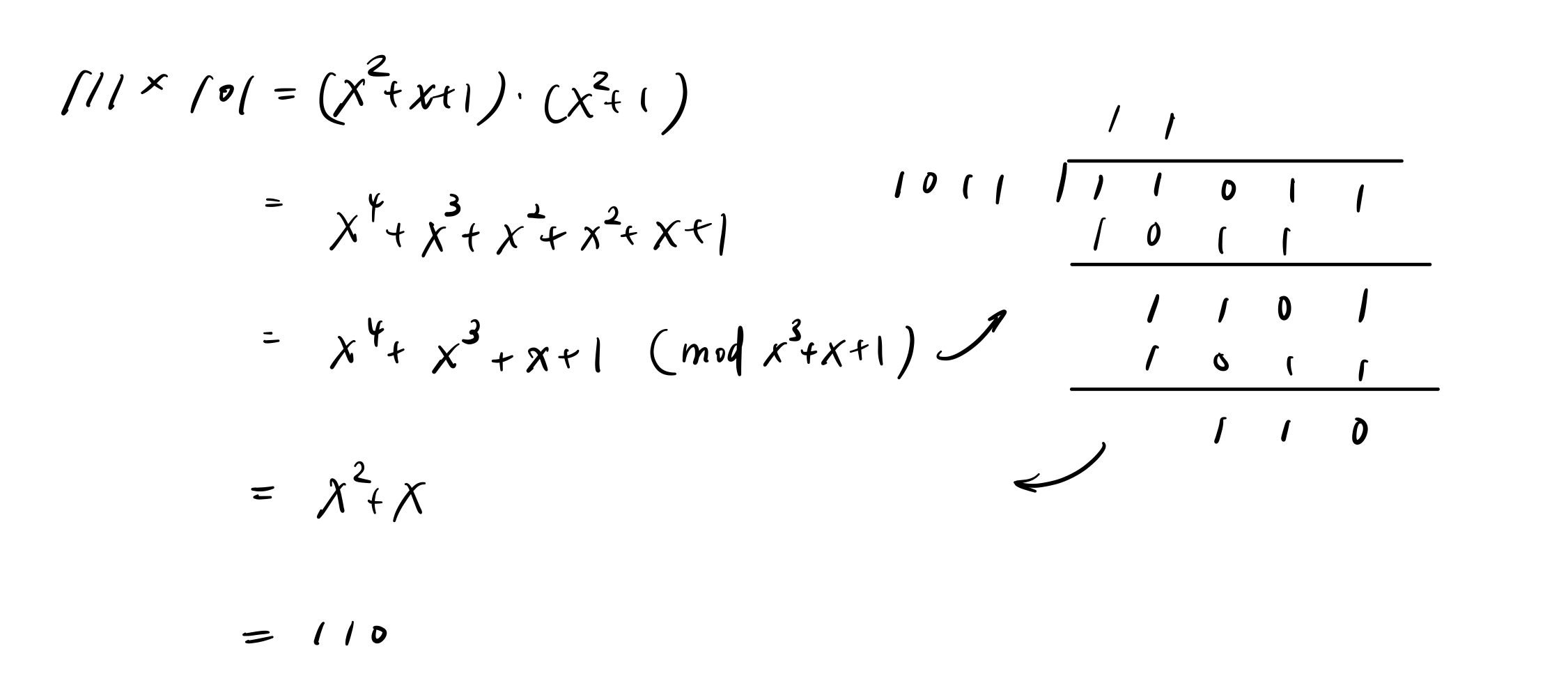
通过这样的运算，我们可以写出整张加法表和乘法表，再把二进制数字的想法搬回来（111=7）。就会出现 $7+5=2$, $7*5=6$ 这样，看似奇怪但很合理的结果。

binary tower

我们定义另外一种 binary field 的构建方式，称之为 binary tower。之所以叫做 tower，是因为每个扩展域都像是上一个扩展域叠加上去，$F{2^{128}}$ 像是两个 $F{2^{64}}$ 结合在一起，而 $F{2^{64}}$ 又像是两个 $F{2^{32}}$ 结合在一起，这样一层一层的感觉就好像一座塔一样。你可以一直无限叠加上去，端看你的需求。

跟原本的 $GF(2^n)$ 一样，每一个位元都表示着一个小的多项式，只是在 binary tower 中，这个小多项式是多变量的，也就是由 $x_0, x_1, x_2,...,x_k$ 组成。

在 binary tower 中的每个元素可以表示成左半边加上右半边乘上 $x_k$，举个例子来说： $$11001010=1100+1010x_2$$ 而其中的 1100 跟 1010 又可以切成一半： $$11001010= 11+10x_1+ 10x_2+10x_1x_2$$ 再切一半就可以得到： $$11001010=1+x_0+x_2+x_1x_2$$

利用同样的算法，我们可以算出每一个位元所代表的多项式，我画了一张图希望更能体现那种塔的感觉，也顺便标示出在每个扩展域中的各个位元代表的多项式是什么：

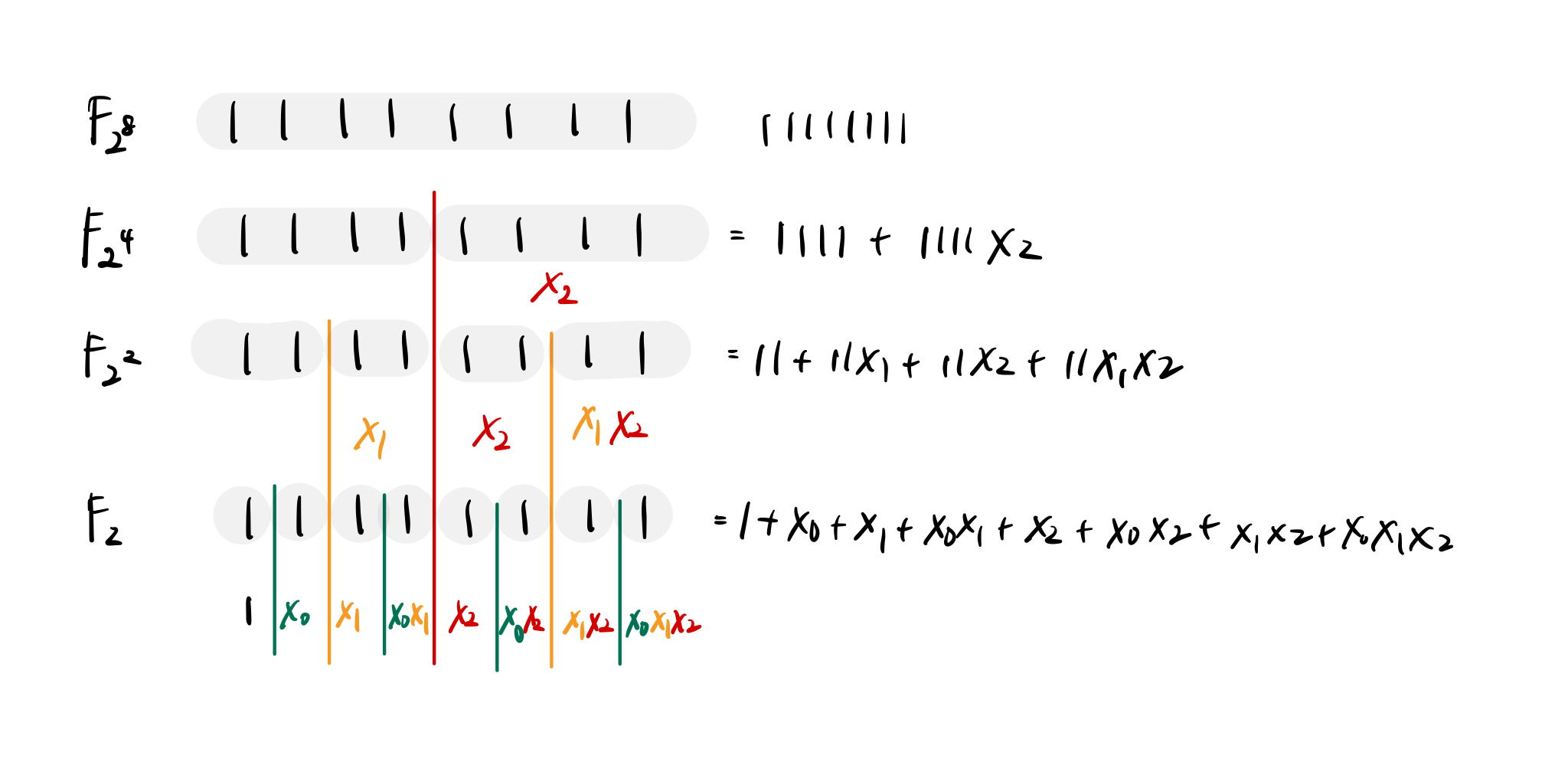
而这么做的好处在于，当我要进行乘法的时候，我可以将两个数字都拆成更小的两个数字，彼此做相乘，然後再拆成更小的数字，这样无限递归下去，最后用很简单的数字完成乘法。

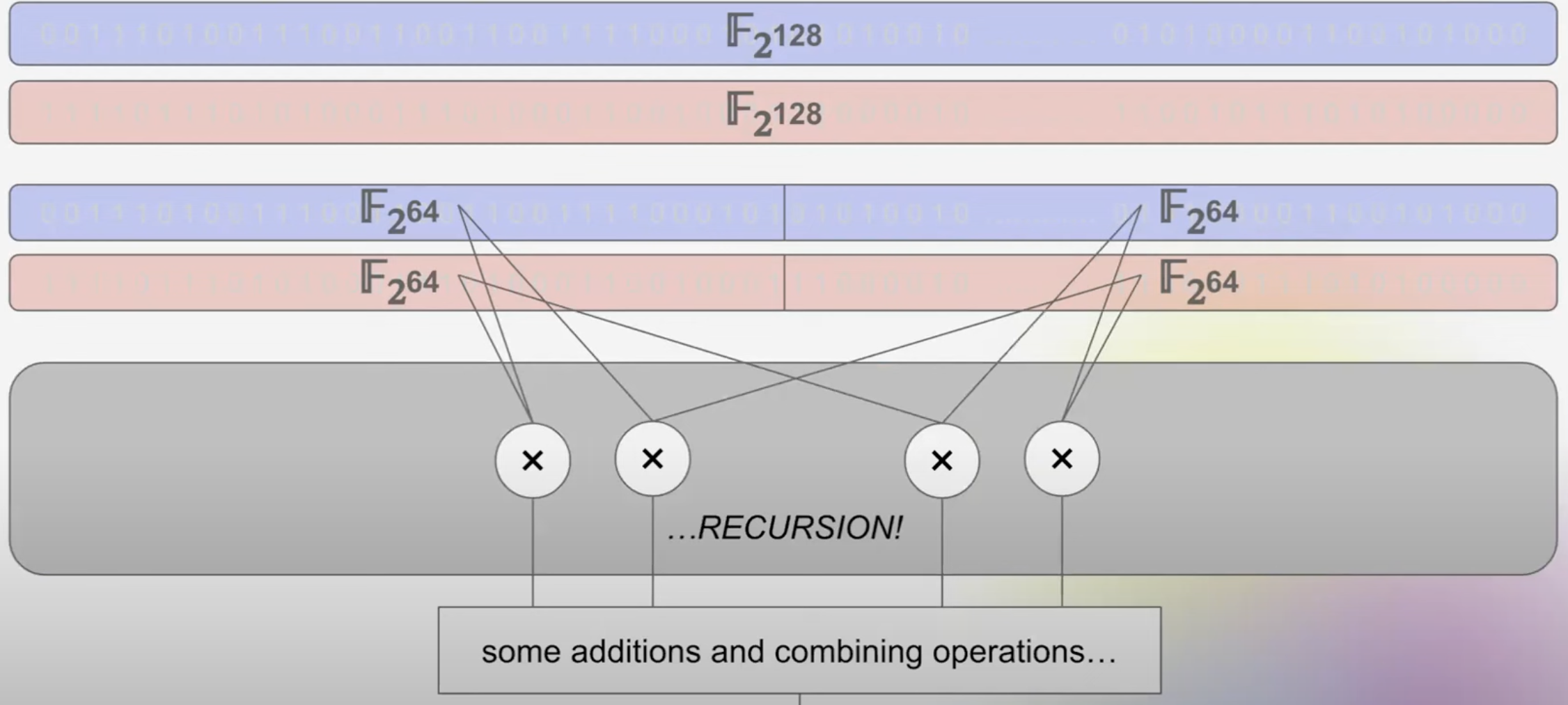（screenshot from https://www.youtube.com/watch?v=eTCjVTWqjj0）

那在这其中会产生一个问题就是，如果次方超过的话怎么办。如同上面的解法，我们同样要定义不可约多项式。换个表示方法，就是把那些有次方的数代换掉：

• $x_0^2=x_0+1$
• $x_1^2=x_1x_0+1$
• $x_2^2=x_2x_1+1$
• ...

所以举个例子： $$\begin{aligned} 54 &= 101001 \ &=(1+x_1)*x_1 \ &= x_1+x_1^2 \ &= x_1+x_1x_0+1 \ &= 1011 \ &= 13 \end{aligned}$$

补充说明一下，这里的二进制表示方法是颠倒过来的，所以 001 代表的是 4 不是 1。那麼根据这样的算法我们可以写出 $F(2^4)$ 之间的加法表和乘法表。读者可以在表中挑一个来手算看看，相信会更容易理解：

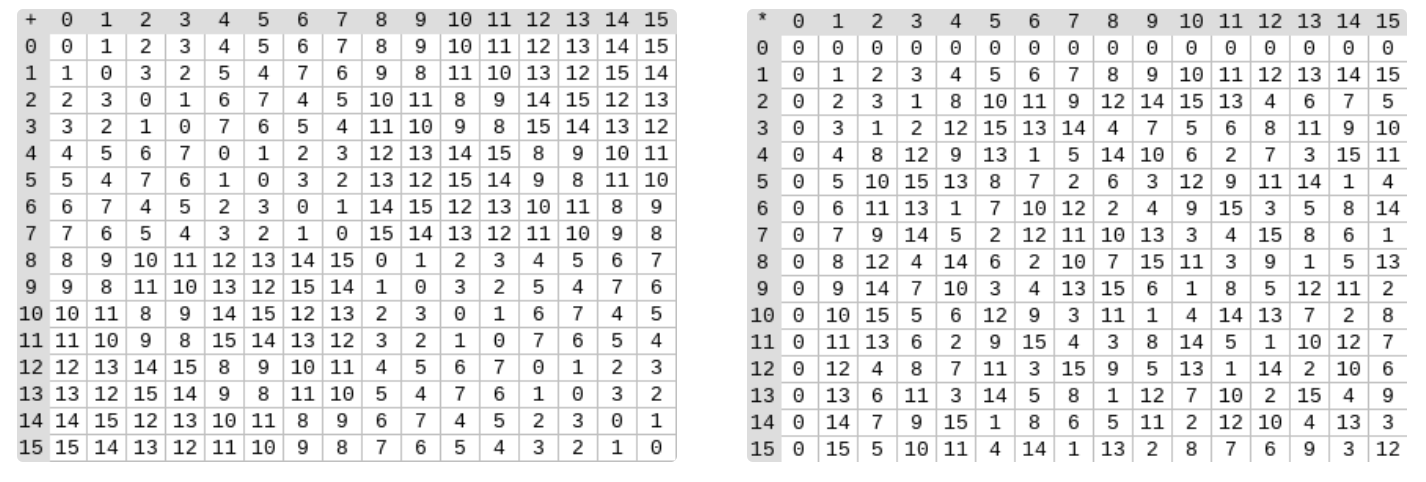(screenshot from vitalik's website)

使用有别于传统构建方式的 binary tower 可以更有效支持各种长度数据之间的运算，在这里我指的是不同数据类型的长度，1 可以就是 1 位元，不用塞到一个 256 位元的空间中。

Reed-Solomon 耗损码

Reed-Solomon (以下简称 RS) 是一种错误更正码（Error Correction Codes），所谓的错误更正码是一种用于在数据传输和存储过程中检测和纠正错误的技术。在数据传输或储存过程中，由于噪音、干扰或其他原因，可能会发生数据的损坏，而我们会利用错误更正码来多传一些附加的信息，让我们可以利用这个信息检测并将损坏的数据恢复成正确的信息。

RS 的做法是将要传的数据看成直角坐标上的点，将这些点计算成为一个唯一的多项式（用拉格朗日插值法），并多传几个多项式上的点作为更正码。这样一来收到数据的人就可以利用多传的更正码还原出原始的多项式，并检查出数据是否有损坏。能承受几个数据损坏由多传了几个数据来决定。

Lagrange 插值

这里简单解释一下拉格朗日插值（Lagrange Interpolation）。给定 $k+1$ 个点，你可以写出一个唯一的多项式： $$L(x) = \sum_{j=0}^ky_jl_j(x)$$

其中

$$lj(x)=\prod{i=0, i\neq j}^k \frac{x-x_i}{x_j-x_i}$$

举个例子：

$$f(1) = 2,\ f(3) = 2,\ f(4) = -1$$

你可以得到：

$$\begin{aligned} l0(x) = \prod{\substack{i=0 \ i \neq 0}}^2 \frac{x - x_i}{x_0 - x_i} = \frac{(x - 3)(x - 4)}{(1 - 3)(1 - 4)} \ l1(x) = \prod{\substack{i=0 \ i \neq 1}}^2 \frac{x - x_i}{x_1 - x_i} = \frac{(x - 1)(x - 4)}{(3 - 1)(3 - 4)} \ l2(x) = \prod{\substack{i=0 \ i \neq 2}}^2 \frac{x - x_i}{x_2 - x_i} = \frac{(x - 1)(x - 3)}{(4 - 1)(4 - 3)} \end{aligned}$$

最后组合起来：

$$\begin{aligned} L(x) &= 2 \cdot l_0(x) + 2 \cdot l_1(x) + (-1) \cdot l_2(x) \ &= 2 \cdot \left(\frac{(x - 3)(x - 4)}{6}\right) + 2 \cdot \left(-\frac{(x - 1)(x - 4)}{2}\right) - \frac{(x - 1)(x - 3)}{3} \ &= \frac{(x - 3)(x - 4)}{3} - (x - 1)(x - 4) - \frac{(x - 1)(x - 3)}{3} \ &= -x+4x-1 \end{aligned}$$

通过拉格朗日差值法，我们可以在给定任意数量的点时快速计算出唯一的多项式。

一个 RS 示例

现在假设我们要传的数据是 (3, 7, 13)，我们可以让要传的数据刚好是某个多项式代 1,2,3 时的值。也就是我们令一个方程式的： $$f(1) = 3,\ f(2) = 7,\ f(3) = 13$$ 用拉格朗日插值我们可以得到这个二次方程式是 $x^2+x+1$。接着我们算出另外两个点（或更多个点）： $$f(4)=21, f(5)=31$$ 接着把（3,7,13,21,31) 一并传出去，这么一来，只要传送过程中的数据损坏数量在 2 以下，我们就有能力算出同一个多项式并把数据还原回来。比如说今天的第二个数据在传送过程中不小心从 7 变成了 2，我就可以用其他几个点算出原本的 7（严格来说只需要额外的一个点）：

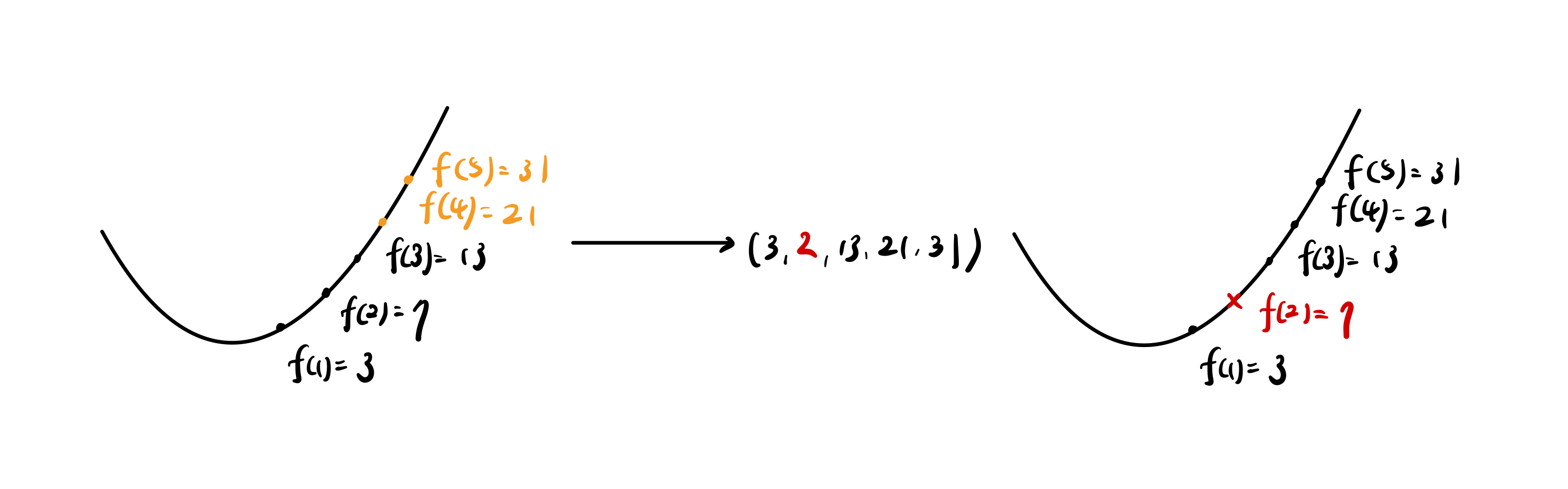
Kronecker 乘积

这里介绍一个 Binius 会用到的小小数学工具，Kronecker 乘积。

Kronecker 乘积是对两个任意大小的矩阵之间的运算，他是一种张量积（tensor product）的特化，以 $\otimes$ 表示。Kronecker 乘积会用两个矩阵生成一个更大的矩阵。举个简单的例子，如果 A 和 B 分别是： $$ A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 5 \ 6 & 7 \end{bmatrix} $$

那么它们的 Kronecker 乘积 $A \otimes B$ 为： $$ A \otimes B = \begin{bmatrix} 1 \cdot B & 2 \cdot B \ 3 \cdot B & 4 \cdot B \end{bmatrix} = \begin{bmatrix} 0 & 5 & 0 & 10 \ 6 & 7 & 12 & 14 \ 0 & 15 & 0 & 20 \ 18 & 21 & 24 & 28 \end{bmatrix} $$

其实他的概念就是把两个矩阵中的元素两两相乘，变成一个更大的矩阵而已。 在 Binius 中我们只会用到两个数组中的 Kronecker 乘积，所以其实只需要了解底下这个例子即可： $$ \begin{aligned} \ [1,2] \otimes [3,4] &= [1\cdot3,\ 2\cdot3,\ 1 \cdot 4,\ 2 \cdot 4] \ &= [3,6,4,8] \end{aligned} $$

Vitalik 的 Binius 示例

在这里介绍 Binius 的整个流程。如果有确实搞懂上面所说的几个概念的话，这张图基本上可以秒杀。我们来一步一步看。

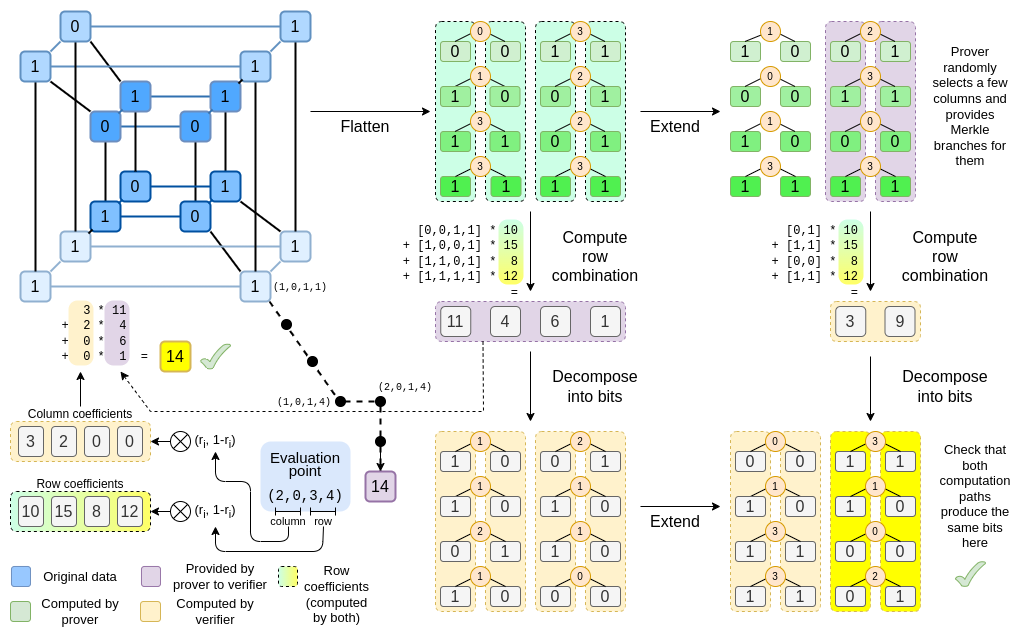(screenshot from vitalik's post)

不同于 KZG commitment scheme，Binius 使用的是多变量的多项式，也就是说要 commit 的多项式不只是平面上的一个曲线，而是一个超方形（hypercube）。你只要想象成原本 commit 的多项式是 $f(x)$，而现在则是 $f(x_1,x_2,x_3,x_4)$。只是前者图像化之后是一个平面上的曲线，后者则是一个五维超方形中的四维超方形。

我们首先将这个超方形拍平成一个 4*4 的表（左上角 Flatten 的部分）。在真实的 Binius 将会是一个更大的表，不过为了方便解释，我们先拿一个小例子来说明。

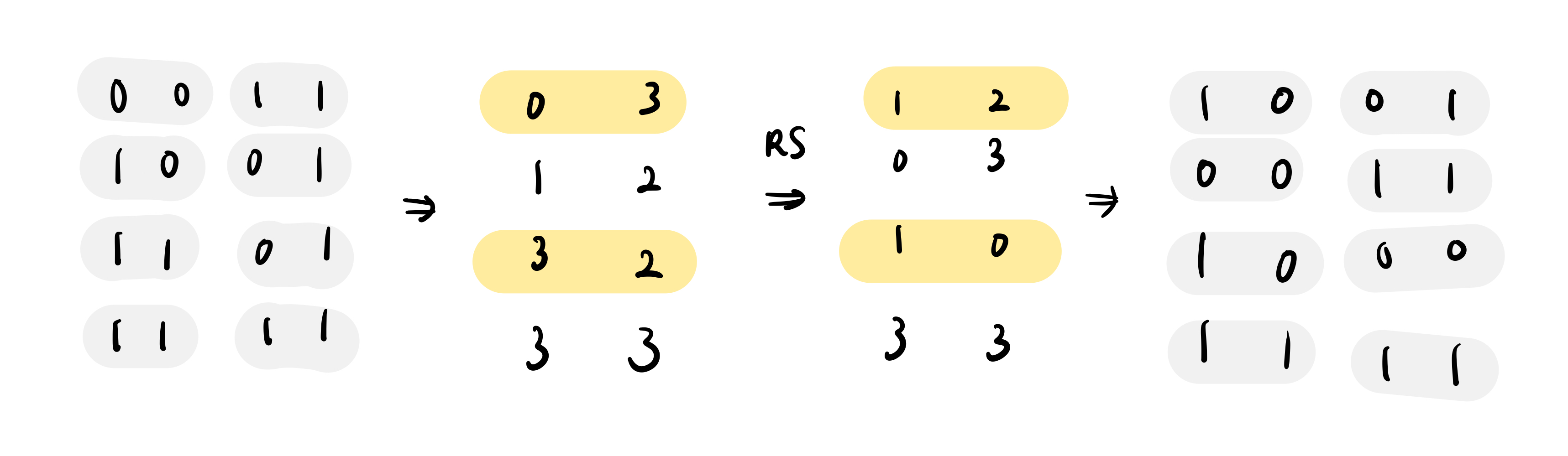
接着我们将拍平后的表两两看作一组，在更大的 binary field 中做 Reed Solomon extension，之后再把 extend 的结果变回 binary。举例来说第一列 $[0,0,1,1]$ 看成 $[00,11]=[0,3]$，对其做 RS，也就是把它看成 $y=3x$，得到 $x$ 代 2 跟 3 的值 $[1,2]$ 再把它转化回 $[1,0,0,1]$。依序对每一列做这样事情。注意到，在这个例子中的所有数字运算都是在 $GF(2^2)$ 之中，所有的乘法跟加法都是使用 binary tower 之中多变量的运算，所以如果你想用手算的话，查表比较快。

最后将每一行看作是 merkle tree 的 leaf，算出一个 merkle root，就可以得到运用 binius 运算的 commitment。

接着当 prover 要证明在这个 hypercube 中点 $r=(r_0, r_1,r_2,r_3)=(2,0,3,4)$ 的值是 14，也就是 $f(2,0,3,4)=14$ ，的时候，他会需要做一些运算。

首先他取后面两位 $(r_2,r_3)=(3,4)$，运算 $(1+r_2,r_2) \otimes(1+r_3, r_3)=(2,3) \otimes(5,4)=(10,15,8,12)$。接着我们将得到的数组跟拍平后的表格相乘得到 $[11,4,6,1]$： $$ \begin{aligned} [0,0,1,1]10+ \ [1,0,0,1]15+ \ [1,1,0,1]\ \ 8+ \ [1,1,1,1]12= \ [11,4,6,1] \end{aligned} $$

Prover 将 $[11,4,6,1]$ 、以及 RS 后的表格中随机挑选的几行数字及其 merkle proof 传给 Verifier 作为 proof。在这个例子我们选最后一行给 Verifier 验证。

Verifier 要做的验证有两个，第一件是验证 merkle root 的正确性。Verifier 拿 Prover 提供的数组 $[11,4,6,1]$ 进行 RS、以及拿 Prover 随机挑选的几行 RS 后的表格乘上 $[10,15,8,12]$ （Verifier 可以自己算这个），这两者算出的结果应该要一样。如果一样就说明 merkle root 是正确的。

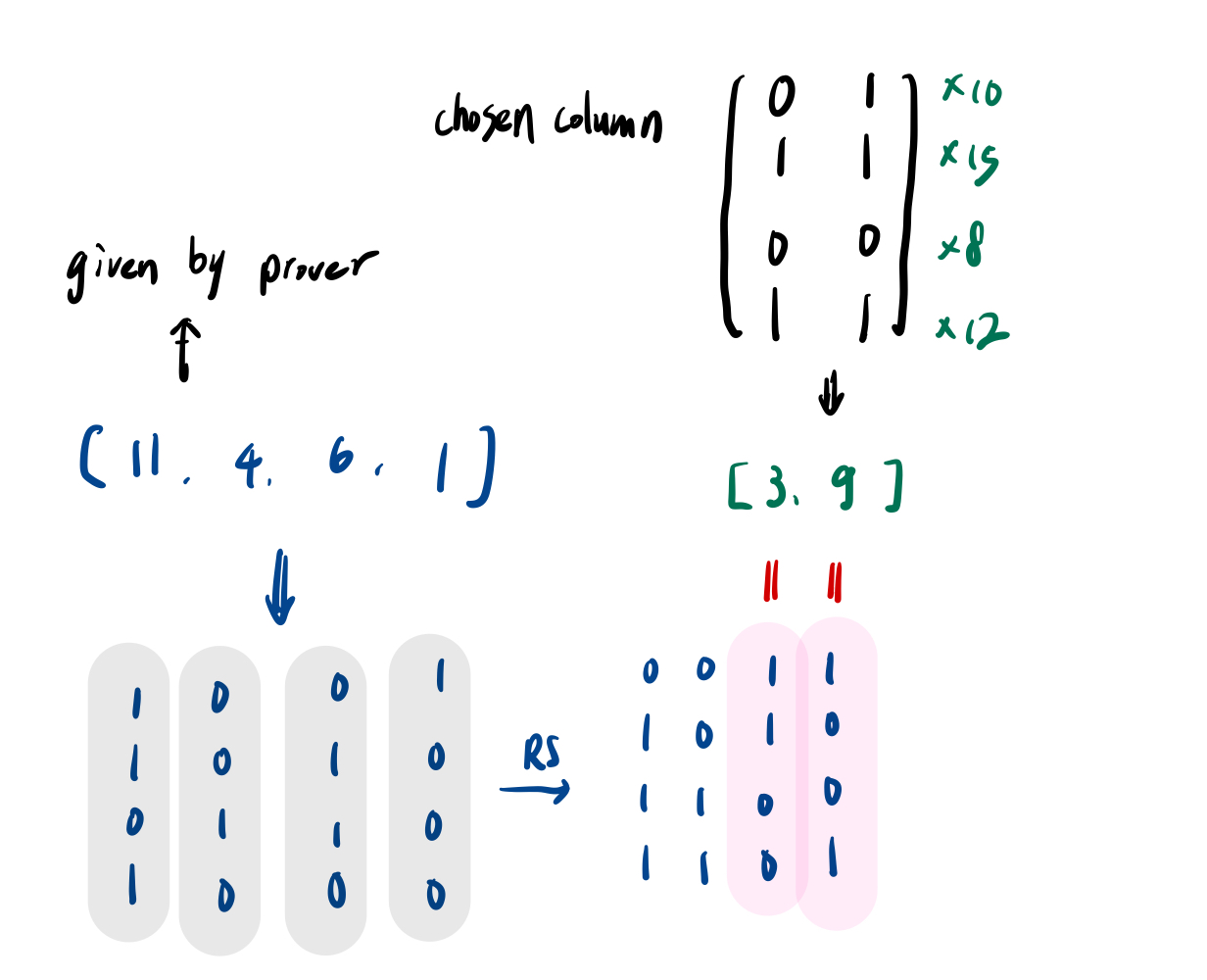
Verifier 要做的第二个验证是验证 $(2,0,3,4)$ 的值真的是 14。他要拿 首先他取前面两位 $(2,0)$，运算 $(1+r_0,r_0) \otimes(1+r_1, r_1)=(3, 2) \otimes(1,0)=(3,2,0,0)$，接着和 Prover 提供的 $[11,4,6,1]$ 相乘得到 $311+24 = 14$。证明了 Prover 所说的 $(2,0,3,4)$ 的值是 14。这样就完成了整个证明的过程。

那么现在再回来看看这张图，读者应该可以完全知道里面的每一个过程跟数字是怎么来的。 (screenshot from vitalik's post)

总结

Binius 通过在 $GF(2^n)$ 中运算，可以有效的减少空间的浪费，并且在表现上比 plonky2 快了 50 倍。

在四月的时候，Irreducible 又推出了一版 FRI-Binius，将原本用 Brakedown 改良的 Binius 改成结合 FRI 和 BaseFold，降低了整个 proof size。而在今年七月的时候，Irreducible 更宣布要和 Polygon Labs 合作建立 Binius-based zkVM。之后应该会有更多与 Binius 结合的成品出现。

参考文献

• Binius blog post by Irreducible
• Binius research paper
• Binius explained by Ben Diamond (video)
• Binius explained by Vitalik
• Understanding PLONK

• 原文链接： github.com/chen-yanlong/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～