零知识证明 - 深入理解PlonK算法
- Star Li
- 发布于 2021-01-29 16:59
- 阅读 13649
PlonK算法实现了Universal的零知识证明。SRS只需要提供比多项式阶高的可信设置即可。PlonK电路采用特殊描述,一个门只支持乘法和加法操作。电路需要证明门的输入输出满足外,还需要证明连线的连接关系。PlonK算法的底层原理是多项式承诺。PlonK算法巧妙地将电路的满足关系通过多项式承诺进行证明并验证。
PlonK,Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge的简称。PlonK算法,实现了Universal的零知识证明算法。所谓Universal,初始可信设置只需要一次,而且可以在原有基础上直接迭代。对Groth16熟悉的小伙伴都知道,Groth16的每一个电路都需要单独的可信设置(Trusted Setup)。
PlonK的论文的下载地址如下:
https://eprint.iacr.org/2019/953.pdf
Plonk的论文相对来说,逻辑性比较强,总共8章。推荐阅读的顺序是第1章(综述),第5章(电路设计),第2/3/4章(基础理论),第6/7/8章(约束系统和协议)。推荐大家有可能还是看看论文。
本文介绍PlonK算法的原理以及整个协议的Prove/Verify的验证过程。
01 初始参数SRS
了解Groth16的小伙伴,很熟悉CRS - Common Reference String。SRS是类似的意义,只是这些数据是Universal的,Structured Reference String。
02 多项式批承诺
多项式批承诺(Batched Polynomial Commitment)原理比较简单,却是PlonK算法的重要基础。多项式批承诺,就是提供多个多项式形式的证明。论文中介绍了单类多项式承诺和多类多项式承诺算法(batched)。
单类多项式承诺
在论文的11页,详细给出了单个多项式承诺的原理,分为三步。
第一步:生成SRS。假设多项式的阶最大为d。随机选取x,生成SRS,对应多项式各个项的两个椭圆曲线上的点。

第二步:生成某个多项式f的承诺。利用SRS,“乘以”多项式的系数,获得最后的多项式的承诺。

第三步:验证者发送gamma给证明者,证明者构造h多项式,并给出多项式对应SRS的点值。验证者验证多个多项式的值和多项式承诺是否一致:
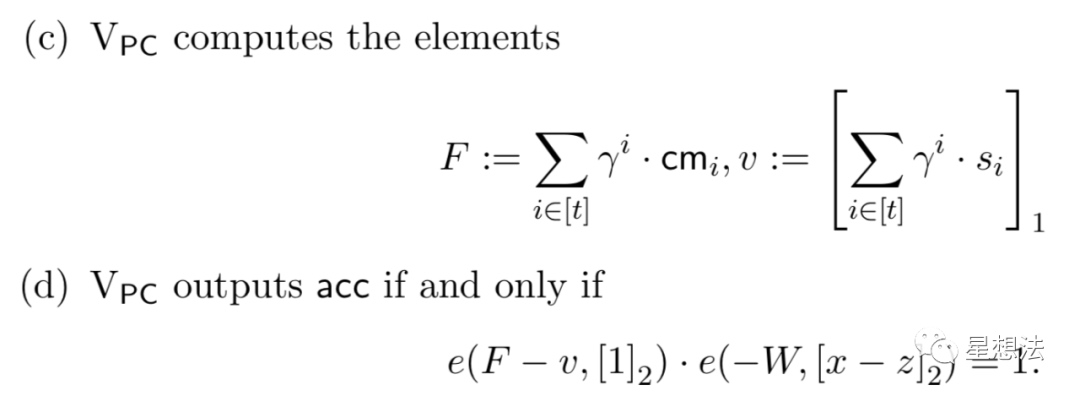
{cmi} - 某个多项式的承诺,{zi} - 多项式的取值(多个多项式的取值都相等),{si} - 多项式的结果。Vpc是验证者,Ppc是证明者。Vpc选择随机数,并发送给Ppc。Ppc计算h(X),并计算出椭圆曲线的点W,发送给Vpc。Vpc计算出F,并通过配对函数验证承诺和值是否一致。在理解配对函数计算的情况下,可信性和完备性的证明都比较简单,感兴趣的小伙伴自行查看论文。
仔细的查看Vpc的F的计算,只是对最后的承诺和多项式值进行计算。公开信息是多项式的承诺以及多项式在某个点“打开”的值。证明者通过计算h(X)证明知道多项式的知识。也就是说,在SRS可信的情况下,证明者并不泄漏任何多项式的具体信息的情况下,验证者可以确定某个多项式的值是可信的。
多类多项式承诺
在单类多项式承诺的基础上,推广到多类多项式承诺。所谓的多类多项式承诺,就是有多个多个多项式,需要证明多项式的值和承诺一致。在PlonK算法中,因为电路的设计的原因,采用的是两类多项式承诺。和单类多项式承诺相比,两类多项式承诺需要Vpc提供两个随机信息。

原理还是比较简单的,(cm-si) + z (cm-si)/(x-z) = x/(s-z) (cm-si)。
03 多项式置换
PlonK的算法原理需要证明多项式置换。这里的多项式置换指的是某个多项式的输入置换(对调)的情况下,输出值相等。
Li(X)
Li(X)代表一个多项式第i项的拉格朗日基函数。在一个有限子群H中,生成元为g,阶为n。如果a等于g^i,Li(a)=1,其他情况,Li(a) = 0。
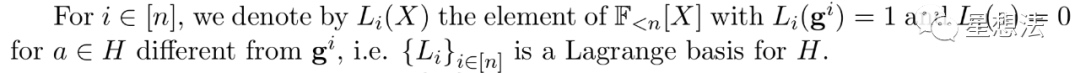
采用Li(X),可以将多项式相等的检查表示为范围的检查:
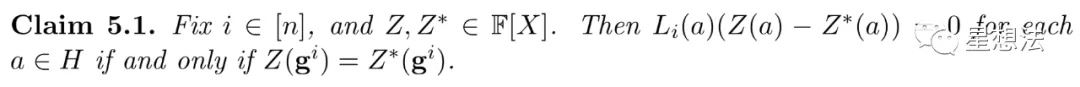
Li(a)(Z(a) - Z (a)) = 0,如果对H中的所有元素都成立的话,有且仅有 Z(g^i) = Z (g^i)。如果a是属于g^i,Li(a)=1,Z(g^i) 必须要和Z * (g^i)相等。如果a不属于g^i的话,Li(a) =0,等式自然成立。
点标记和置换
在介绍多项式置换之前,需要定义多项式输入的位置(ID)。因为在有限域,输入是g^i,输入间接可以用i在表示。SID是个顺序标号。Sigma(i)是置换函数。
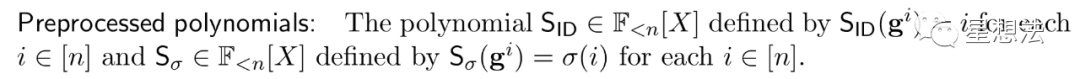
置换协议
所谓的置换,类似于如下的情形:
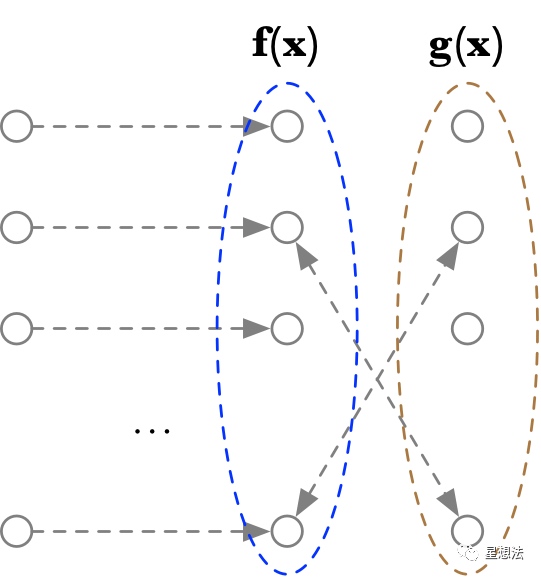
一个多项式的值发生对应关系的“置换”。
置换协议也分两种情况:1/ 同一个多项式的输入置换 2/ 多个多项式的输入置换。这两种情况是针对需要置换多项式的个数进行区分。
同一个多项式的输入置换的协议如下:

f'和g'是新的函数,将f和g函数的输入和输出值进行“累加”。为了防止f函数的信息泄漏,采用了beta和gamma两个随机因子。Z函数需要理解清楚:Z函数是f'/g'的连乘函数(b),并且Z(g)=1 (a)。简单的推理就能得出,如果只是输入信息发生置换的话,Z(g^n) = 1。
由如上的Z函数的定义,可以确定Z(g^n) = 1,也就是说,f/g函数按照指定的规则进行置换。
多个多项式的输入置换的协议如下:
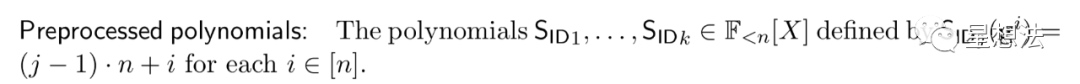
点标记会扩大到多个多项式,简单的说,多个多项式的输入信息连续编号。

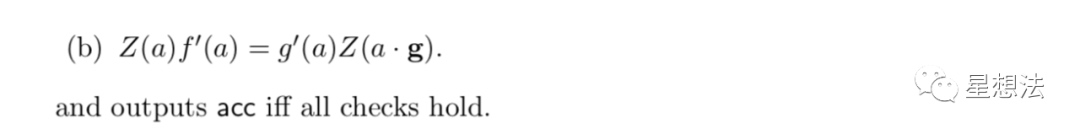
在原来的同一个多项式协议的基础上,首先把多个多项式连乘,然后再计算Z函数。总而言之,通过验证两个多项式可以确定多项式的置换。置换协议也是后面要讲到的“copy contraint”的基本原理。
04 Fiat-Shamir启发式算法
Fiat-Shamir启发式算法又分为两种:交互式和非交互式。感兴趣的小伙伴,可以查看wiki的介绍。
https://en.wikipedia.org/wiki/Fiat–Shamir_heuristic
交互式:
为了证明Peggy知道某个值x,并且y=g^x,Peggy和Victor各选择一个随机数:v和c。Peggy提供g^v和r=v-cx,Victor就能验证。
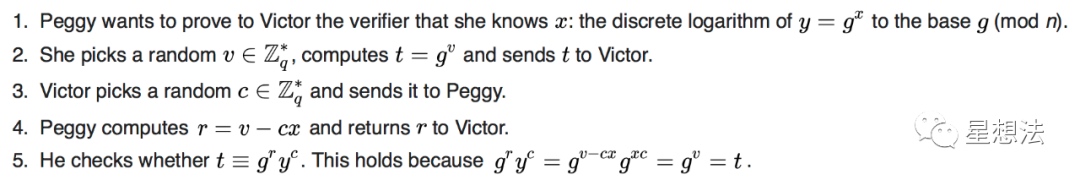
非交互式:
交互式的算法中,Victor需要提供一个随机数。在非交互式的算法中,这个随机数,通过公开信息的hash函数的结果代替。

PlonK协议采用的是非交互式。
05 电路原理和约束系统
Vitalik有一篇介绍PlonK的博客,详细介绍了电路的原理。
https://vitalik.ca/general/2019/09/22/plonk.html
我之前也写过一篇PlonK电路的理解:
简单的说,这张图给出了PlonK算法下电路的样子。电路由加法门或者乘法门组成。
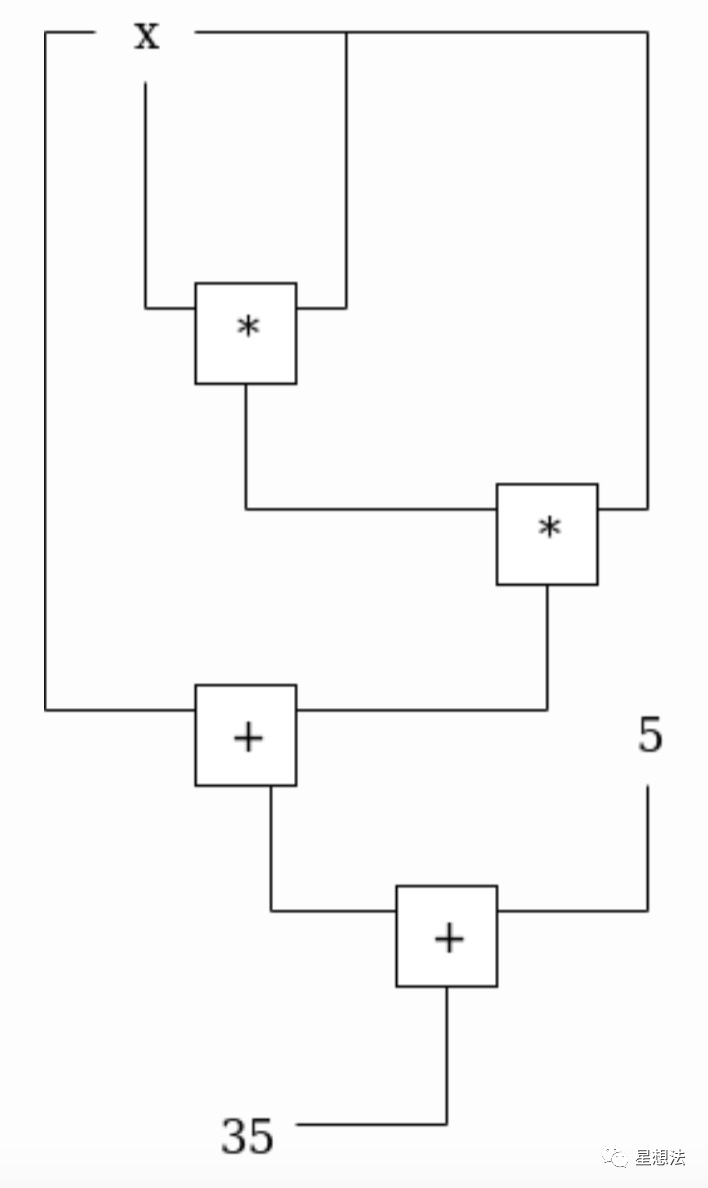
所谓的约束系统,就是电路形式的约束表示。电路中的每个门就是一个约束。论文给出了2输入,不限输出的电路的表示。假设一个电路由n个门和m个线组成,其中n<=m<=2n。约束系统由两部分组成:1/每个门输入信息 2/门约束的系数向量。

V是由左输入a,右输入b,以及输出c的向量组成。注意的是,a/b/c只是序号。qL,qR,qO,qM,qC是门的选择算子向量。L代表左,R代表右,O代表输出,M代表乘法,C代表常量。
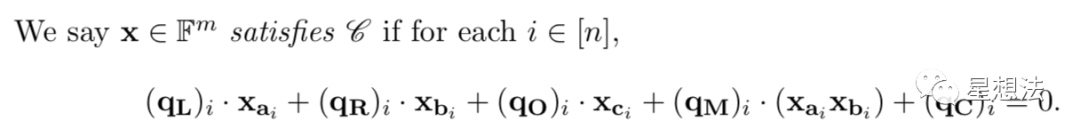
整个电路,满足如上的等式。也就是说,在一个约束中可以表示一个加法和一个乘法。在这个定义的基础上,论文给出了三种具体电路的表示方式:1/算术电路(乘法和加法)2/布尔值限定 3/公开输入限定。公开输入限定可以理解成限制某个输入等于固定值,并且该固定值是公开的。
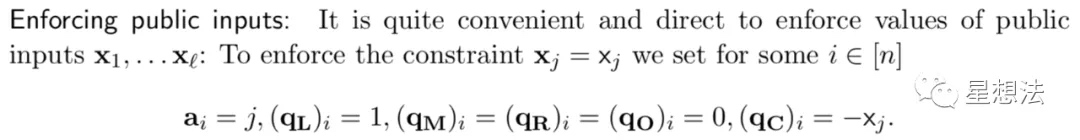
总结一下,PlonK的约束系统:

fL/fR/fO分别是左/右以及输出的函数表示。该约束系统约束了两个逻辑:
1/ copy contraint - 也就是门和门共用的wire是正确的
2/ 每个门的约束成立
明确一些逻辑意义。2输入,不限输出的电路,如果有n个门,存在最多2n个输入,用m表示。每个门的左右输入以及输出,采用下标表示ai,bi以及ci,其中 0X中的编号。Xai是输入或者输出具体的值。所谓的置换,是i的变换。一句话,输入或者输出表示成函数后,在某两个变换值的取值相等。也就限制了某个门的输入和输出和另外一个门的输入或者输出相连。PLONK的电路表现形式比R1CS弱一些:PLONK的一个门只有一个加/乘,R1CS支持累加后乘。
06 PlonK协议
论文的最后一章,第8章给出了整个PlonK协议的全貌。整个PlonK协议基于多项式承诺以及Fiat-Shamir启发式算法。给定3n个witness,并且给定多项式的门系数向量以及置换函数,证明每个门的约束成立:
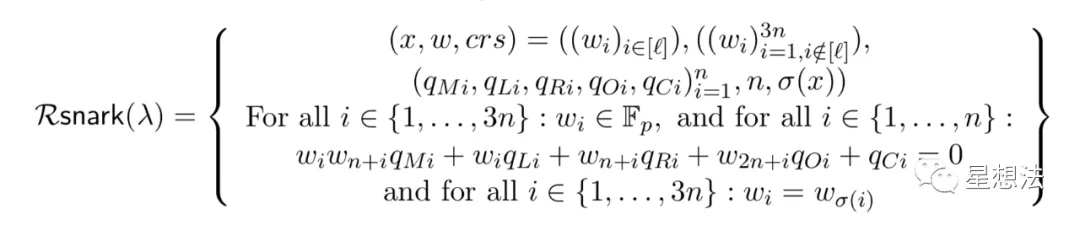
公开信息
PlonK协议公开的信息,包括门的系数,置换函数,以及公开输入。

证明过程
证明的计算过程分为5轮。
第一轮:
计算出a(X),b(X),c(X)的多项式表示,并计算出SRS对应的椭圆点。a/b/c对应协议中的fL/fR/fO。

第二轮:
利用Fiat-Shamir启发式算法生成随机数,并计算出z(X)的多项式表示,并计算出SRS对应的椭圆点。

第三轮:
利用Fiat-Shamir启发式算法生成随机数,并计算出t(X)的多项式表示,并计算出SRS对应的椭圆点。
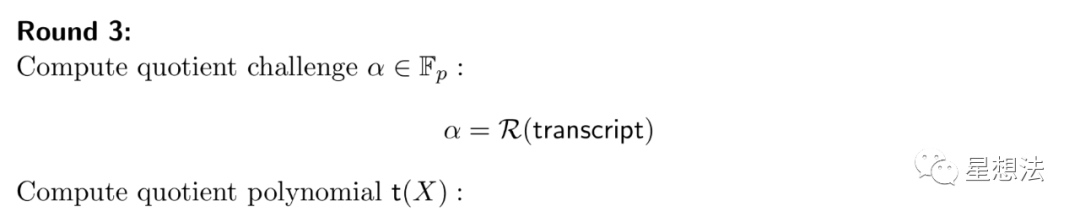
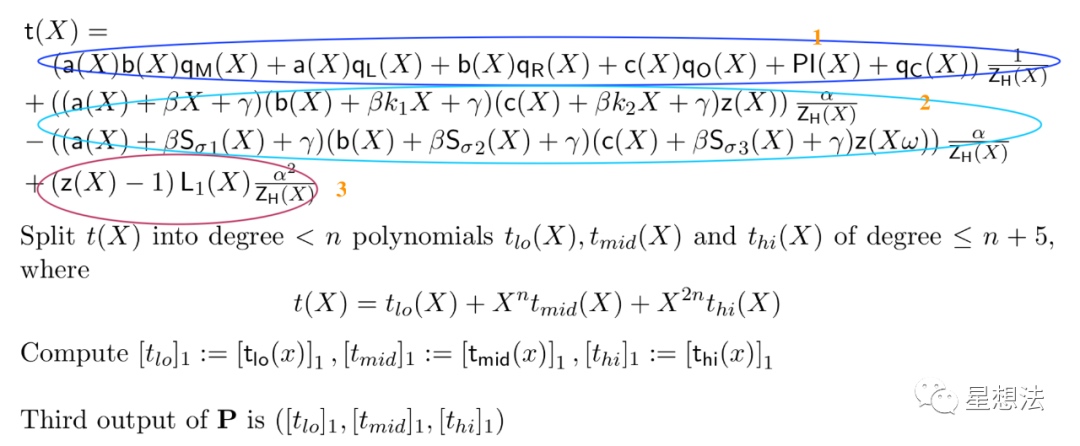
注意,t(X)是核心,融合了三个多项式等式:
1/ 第一个等式限制门电路满足
2/ 第二个和第三个等式满足“copy contraint“,门和门之间的连接满足。
第四轮:
第一轮到第三轮都是计算多项式承诺。从第四轮开始,计算的是具体的点对应的椭圆点。
利用Fiat-Shamir启发式算法生成随机数。计算a/b/c/t/z以及置换函数对应的函数值。

定义并计算r函数,以及r函数对应的值。注意r函数和t函数有关系,具体的关系在验证过程介绍。
第五轮:
利用Fiat-Shamir启发式算法生成随机数,并计算多类多项式承诺的证明。证明的多项式是两类:1/ a/b/c/t/r以及置换函数 2/ z函数。

验证过程
验证过程除了一些简单的数据检查外,核心的验证逻辑如下:

从12步看起,整个验证过程只需要验证一个多类多项式承诺。核心计算是 F - E。F是多个多项式的承诺对应值,E是多个多项式的挑战对应的值。多类多项式承诺算法保证了,挑战对应的值,和承诺一致。F计算中的D就是r和z函数组成。
如何约束?
细心的小伙伴,肯定会有疑问,这一堆计算怎么保证电路的约束满足的?即使多类多项式承诺和挑战一致,也只是保证了如下的函数是多项式形式:
- a/b/c 2. r 3. z 4. t 5. 置换函数
仔细查看D的计算(包括证明的r函数),发现D并不是由证明者提供。也就是在证明过程,r函数的承诺值并没有提供。验证者自己计算出D的承诺值,也就是限制了D的多项式表达式。
在确定了D的多项式表达式后,也就是确定了间接证明了r函数的表达式。
从第8步的计算,给出了t函数挑战对应值的计算公式。因为r函数的表达式确定,从而也确定了t函数的表达式。再仔细查看证明过程中的t函数表达式,因为t函数能被ZH函数整除,就是说明分子表达式在根的取值都为0,也就证明了电路的三个多项式相等。
07 计算量比较
论文的第1章给出了PlonK算法和其他算法的性能对比。
证明性能

假设乘法门的个数n,加法门的个数和乘法门个数相等a=n,wire的个数m是总的门数的两倍m=4n,并且G2的计算是G1计算的3倍,则:
1/ PlonK的SRS大小是Groth16的1/4左右。
2/ PlonK的证明的计算量是Groth16的1.8倍左右。
3/ PlonK的证明大小是Groth16的2.5倍左右。
验证性能
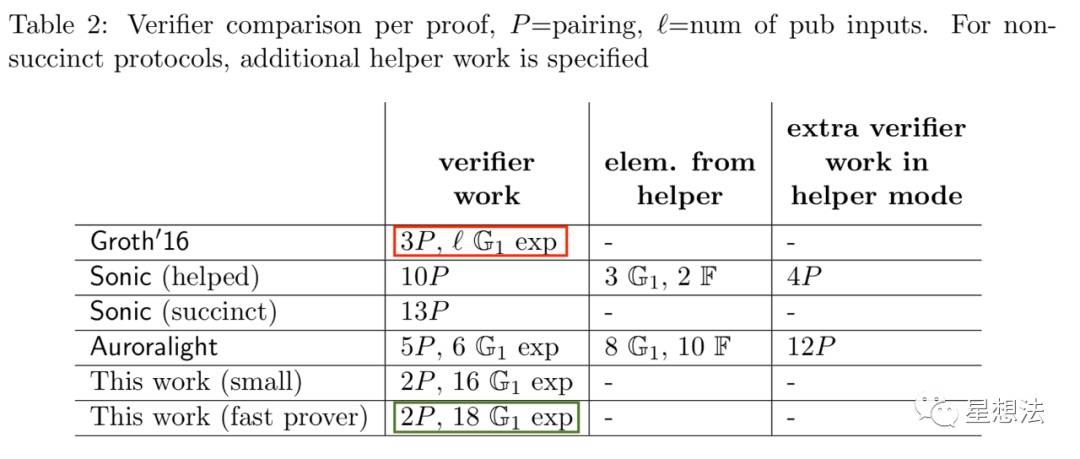
PlonK的验证时间和Groth16差不多。
总结:
PlonK算法实现了Universal的零知识证明。SRS只需要提供比多项式阶高的可信设置即可。PlonK电路采用特殊描述,一个门只支持乘法和加法操作。电路需要证明门的输入输出满足外,还需要证明连线的连接关系。PlonK算法的底层原理是多项式承诺。PlonK算法巧妙地将电路的满足关系通过多项式承诺进行证明并验证。

- Zero 链: 技术定位报告 108 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 102 浏览
- 以太坊 2029 Strawmap 傻瓜指南 187 浏览
- 不实的断言:攻破 6 个 zkVMs 127 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 244 浏览
- 零知识编年史:群 200 浏览
- 以太坊执行层优化:状态树与虚拟机 353 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 271 浏览
- 首次 ZK 攻击发生,且出乎意料 279 浏览
- Vitalik: 以太坊量子抵抗路线图 243 浏览
- zkMesh:2026年2月回顾 296 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 302 浏览

