没有 Diffie-Hellman，只有椭圆曲线 Diffie-Hellman

当我第一次学习 Diffie-Hellman，尤其是椭圆曲线 Diffie-Hellman 时，我有一个相当明显的问题：为什么是椭圆曲线？为什么使用这个看起来相当随意，带有一条线的三次交点然后反射的奇怪群？为什么不使用，比如怪物群？当然，一个怪物比一些以曲线命名的，但在法律上与完全不同的曲线事物不同的曲线东西，更能保护你的秘密！

直到我研究生学习的后期，我才对这个问题有了一个令人满意的答案，这个答案对于本博客的“密码学（难以理解）”类别来说是一篇完美的博文，所以我们开始吧。

群

首先，作为回顾，我们所说的 Diffie-Hellman 是什么意思？嗯，我们需要一个群 $G$，以及这个群的元素 $g \in G$，它具有某个阶 $p$，因此 $p$ 是满足 $g^p = e$ 的最小正整数，其中 $e \in G$ 是该群的单位元。然后我们取我们的私钥 $s \in \mathbb{Z}/p\mathbb{Z}$，并将我们的公钥计算为 $p = g^s$。我们现在可以使用一些其他的公钥 $q = g^r$ 计算一个共享密钥，如 $K = q^s = g^{rs} = g^{sr} = p^r$。

这应该适用于任何群 $G$，不是吗？那么为什么它不适用于怪物群呢？让我们仔细看看从私钥计算公钥的映射（事实上，这篇博客的其余部分将只关注该映射，整个密钥交换的事情实际上并不重要，你也可以计算 Schnorr 签名或其他什么）。给定任何群元素 $g \in G$，我们总是可以创建指数映射 $\mathbb{Z} \to G\colon k \mapsto g^k$。这个映射是一个群同态，并且不一定是单射的。事实上，对于有限群，它从来都不是单射的。在代数中有一个古老的技巧，你可以通过将定义域除以它的核来使任何群同态都是单射的。这里所讨论的核是理想 $(p)$，即我们阶 $p$ 的所有倍数，所以将我们的密钥空间设置为 $\mathbb{Z}/p\mathbb{Z}$ 是一个明智的第一步，没有任何缺点，允许所有整数并不能真正获得新的密钥。但是，该映射也不一定是满射的。事实上，该映射的像是精确地 $\langle g \rangle$，即 $G$ 的子群，由生成元 $g$ 的所有倍数组成（这就是为什么我们称 $g$ 为生成元，它生成整个东西）。

因此，我们可以通过查看 $\mathbb{Z}/p\mathbb{Z} \to \langle g \rangle \colon k \mapsto g^k$ 来稍微简化我们的私钥到公钥的映射。这样，我们的私钥到公钥的映射不仅是一个群同态，而且还是单射的和满射的，换句话说，是一个群同构。

关于有限单群的题外话

这给了我们第一个关于“为什么不是怪物群？”的答案，尽管这是一个会引出更多问题的答案。为了得到这个答案，我们必须问一个更深层次的问题，即，到底有哪些群？我们想在计算机上工作，所以有限的会更好，而且我们听说过小型子群攻击，所以请使用没有正规子群的群。（如果你不知道什么是正规子群，你可以从一个群中划分出这些东西）。换句话说，一个有限单群。

20 世纪数学中最令人印象深刻的成果之一必须是有限单群的分类。对“到底有哪些群？”这个问题（不太）最终的答案。

为了对群进行分类，我们需要弄清楚两个群相同是什么意思。显然，时钟上的数字和 $\mathbb{Z}/12\mathbb{Z}$ 是同一件事，即使时钟使用罗马数字。因此，简单地重新标记群元素不应被视为不同的事物。换句话说，我们想对同构意义上的有限单群进行分类。

这个分类问题的答案绝对令人难以置信：首先，存在无限的群族。例如 $C_p$，具有素数阶的循环群。另一个这样的族是交错群，从 $A_5$ 开始。还有 16 个这样的无限族，其他的据说属于“李型”。然后有 26 个群，它们只是自己独立存在。它们不是无限族的一部分，它们只是存在，并且没有办法使它们更大或其他任何东西。上面提到的怪物群是其中最大的一个，我完全不是因为它的名字很酷才在引言中选择它的，而且让我跑题去讲零星群了。

但是，有了这种分类方法，我们现在可以发现一个问题（我们本可以在陈述分类结果之前发现这个问题，但是，拜托，这是一个很酷的结果！）。也就是说，为了回答“有哪些群”这个问题，我们必须说我们要研究同构意义上的群。但是我们的私钥到公钥的映射是一个群同构！对于一个群论学家来说，$\mathbb{Z}/p\mathbb{Z}$ 在某种程度上不同于 $\langle g \rangle$ 这种想法是荒谬的，它们显然都只是 p 阶循环群 $C_p$！

范畴

所以，呃，我们有点——意外地——通过问一个天真的问题，即为什么我们使用椭圆曲线而不是任何其他群来进行 Diffie-Hellman，已经在 Diffie-Hellman 的整个概念上炸开了一个大洞。如果私钥空间和公钥空间是同一个，那么 Diffie-Hellman 怎么可能存在呢？如果我们甚至无法区分私钥和公钥，它怎么可能是安全的呢？

好吧，我们已经在和群论学家交谈，并且正在经历一场存在危机，所以为什么不屈服并让他们把我们拉得更深，进入范畴论学家的领域呢？事情不可能变得更糟，不是吗？

一个范畴是一类对象，使得对于任何两个对象 $X, Y$，都存在一个从 $X$ 到 $Y$ 的同态的类 $Hom(X, Y)$。同态只是这个类的元素。我们慷慨地要求在 $Hom(X, X)$ 中存在一个恒等同态，并且存在一个合成运算，其中 $f \in Hom(X, Y)$ 和 $g \in Hom(Y, Z)$ 的存在会给你一个同态 $h = g \circ f$，但仅此而已。特别是，我们甚至不一定要求我们的对象是集合。我们绝对不要求我们的同态是函数。事实上，只是为了防止任何人产生任何愚蠢的想法，当我们不称它们为同态时，我们称它们为箭头。一个范畴真的更像一个有向图。一个有如此多顶点的图，它们不一定适合放在一个集合中，并且其中两个顶点之间可能有如此多的边，以至于它们也不适合放在一个集合中。这就是为什么我们在上面说类的原因，一个类是一个可能比任何集合都大的事物集合。例如，存在一个所有集合的类，但不可能存在一个所有集合的集合，因为没有人知道如何剃掉它们或类似的东西。事实上，写为 SET 的集合就是一个范畴的例子。对象是集合，而同态是这些集合之间的函数。

为了不完全漂移到太空，我们将只关注局部小范畴。局部小范畴是指同态实际上确实形成一个集合的范畴。这使得生活变得更加简单，并且几乎涵盖了我们想要了解的一切。

因此，除了 SET 之外，还有哪些范畴的例子？为什么这个有点单薄的定义最终如此有用，以至于它突然迫使整个数学领域都陷入了抽象的无意义？事实证明，几乎所有事物都可以被视为一个范畴。图？范畴。群？范畴。环？范畴。域？范畴。拓扑空间？范畴。解析簇？范畴。代数簇？你可能已经猜到了，也是一个范畴。向量空间？范畴。模？范畴。

事实证明，如果你对事物的唯一要求是它们以某种方式具有一些像函数一样作用的同态，那么你可以引入几乎所有人类已知的数学对象。但它有用吗？我们甚至没有将我们的对象定义为集合，但我上面给出的所有例子都是集合。当然，比荒谬的无限有向图更具体的东西会更好吗？事实证明，范畴非常有用。你确实必须以有点笨拙的方式重新定义术语，但是一旦你这样做了，你就可以同时对域、环、群、向量空间、拓扑空间等做出陈述。例如，我们不再可以将核定义为映射到零的所有元素，因为请记住，对象不一定是集合，因此它们不一定具有元素，因此我们必须说一些花哨的词，例如“具有零同态的局部小范畴中同态 f 的核是同态 k，当与 f 组合时为零，并且在该属性中是通用的”。今天我们并不完全需要那个完整的工具（特别是，我们不需要通用属性），但我们确实需要稍微简单一点的初始对象和终端对象的概念。初始对象 $I \in \mathcal{C}$ 是这样一个对象，对于任何 $X \in \mathcal{C}$，$Hom(I, X)$ 恰好有一个元素。终端对象 $T \in \mathcal{C}$ 是对偶对象，即对于每个 $X \in \mathcal{C}$，我们在 $Hom(X, T)$ 中恰好有一个元素。如果一个对象既是初始对象又是终端对象，我们称这个对象为零对象，并且它对于给定的 $X$ 具有的唯一同态称为零同态。例子对于这一点很重要，所以让我们首先看看 SET。这里的初始对象是空集，因为存在一个从空集到任何给定集合的唯一函数（空函数）。然而，空集不是终端对象，因为不存在从非空集到空集的函数。相反，恰好具有一个元素的单例集取代了终端对象的位置。当我们观察 GROUP 时，我们看到了一个具有零对象的范畴的例子，即仅由单位元组成的平凡群。存在一个从平凡群到任何给定群的群同态，因为群同态必须将单位元映射到单位元，并且存在一个从任何给定群到平凡群的群同态，该同态通过将所有内容映射到单位元来给出。为了结束我们的例子，一个稍微有趣的例子是（可交换）环的范畴 RING。我们的终端对象再次是仅由元素 0 组成的平凡环，但它不能是初始对象，因为环同态需要将 1 映射到 1，而平凡环只有一个元素，不能将该元素同时映射到 0 和 1。相反，环的范畴的初始对象是整数 $\mathbb{Z}$。最通用的循环群。

群对象

我们又在说什么来着，哦，对了，Diffie-Hellman。因此，凭借范畴理论的语言，我们现在可以准确地指出为什么“任何群都应该有效”是不起作用的。只要我们只关注群，我们就必须关注同构意义上的群（否则对事物进行重命名就会成为不同的事物），但是我们的私钥到公钥的映射是一个群同构。我们没有看正确的范畴。Diffie-Hellman 不适用于群。

我们必须深入研究。

输入群对象。我喜欢这个话题。事实上，我曾经写过整整 90 页关于它的漫谈小说，然后人们说我现在可以称自己为医生了。

相关部分在第 3 章中，夹在大量的抽象废话之间。

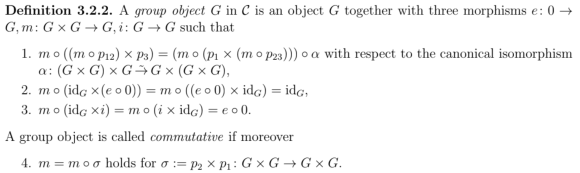
为了更详细地介绍它，我们有一些范畴 ，我们将其用作我们的基础。我们想将该范畴中的某个对象 变成一个群。但请记住，这是范畴理论，因此 不一定是集合。我的意思是，在任何实际情况下它都是一个集合，但我们可以假装我们不知道这一点，为了做一些非常非常酷的数学。当假装你不知道某些东西会导致一些非常非常酷的数学时，你总是应该假装你不知道它。所以我们拥有的唯一东西是同态。在章节中裁剪掉的部分中，我们确实将事情缩小到具有终端对象的局部小范畴，并将该终端对象命名为 。因此，如果我们没有元素，我们如何描述群公理？好吧，第一个公理，结合律，是关于乘法的。乘法是一个映射，将群的两个元素映射到一个元素，所以我们可以简单地说我们要求该映射是 中的同态（如果 不是集合，请不要问 是什么。这是关于通用属性的，我保证不会有通用属性）。为了定义结合律，我们需要 与 相同。这是由于我们不谈论的通用属性，但它给了我们这个规范同构，即这两个构造是相同的，并且它们以某种非常明显的方式是相同的。现在结合律只是说乘法态射，以一种顺序应用两次，与乘法态射以另一种顺序应用两次相同，你可以在截图中看到第一个属性。类似地，交换律也只是关于乘法态射的陈述，具有另一个规范态射，解释了第四个可选属性。

更有趣和更酷的是第二个属性，它定义了单位元。那么，当你非常努力地假装你没有任何元素时，你如何定义单位元？这就是我们的终端对象发挥作用的地方。我们将一个元素 指定为中性态射。请注意， 是_终端_对象，而不是初始对象，因此 不一定是唯一的。事实上，如果我们以集合范畴作为我们的基础（这将给我们带回我们所知道和喜爱的群），那么如上所述，终端对象是单例集。从单例集到集合的映射可以被视为指向我们的目标集合中的一个特定元素。换句话说，集合范畴中 的一个元素只是 的一个元素。现在我们需要描述是什么使单位元成为单位元。它应该以某种方式与我们的乘法态射相互作用。我们现在执行我们定义中最神奇的部分。我们想要定义中性属性，即 ，但不提及 ，而是将其表述为一系列映射。让我们暂时保留 一段时间，以便制定一个作战计划。由于我们想要谈论 ，我们想要使用前缀表示法而不是更熟悉的 infix 表示法，对 做出陈述。所以我们需要构造 ，理想情况下从 开始，这样我们最终可以得到一个很好的等式。因此，从单个元素开始，我们想要两个。有一种方法可以做到这一点，即使用对角态射 。这不太像是 ，但至少它有两个组件。第一个组件我们可以保持不变，换句话说，我们将其应用于单位元。但是我们如何摆脱第二个组件？好吧，我们可以将其映射到我们的终端对象 0。只有一种方法可以做到这一点。现在我们在 0 中，我们可以应用我们的中性态射 返回到 。如果我们用 表示我们的终端集合 中的唯一元素，并用 表示我们群中的单位元，我们可以执行如下的映射链：。现在我们可以应用 并期望最终到达相同的位置。换句话说 。突然间，我们描述了单位元的作用，而没有你所知道的元素。

最后一个关于逆的属性使用了类似的构造，这次使用另一个从群对象到它自身的映射来寻找逆。我留给读者去研究为什么它必须看起来完全是这样的。

寻找我们的范畴

有了这些，我们现在终于有了实际回答我们最初问题的工具。我们要映射到什么东西中？我们对此有什么选择？我们已经确定它不是一个群，因为群将无法区分私钥和公钥。我们需要一些额外的结构，一些告诉我们如何对我们的东西的元素进行操作的东西，而不是说 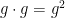仅此而已。虽然我们仍然需要一些表现得像群的东西，因为所有关于密钥协商的东西从根本上都依赖于存在一些群的东西。我们需要一个群对象。但是我们用作基础的范畴 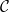是什么？它不能是 SET，因为它会直接带我们回到群。我们可能想要一些具有有限对象的对象，因为计算机不太擅长处理不适合它们的小型存储器、磁盘和寄存器等的东西。我们确实希望能够计算至少乘法态射 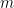。我们将需要少量的挥手示意，但我认为不难看出将有限域元素的元组作为基础可能是一个好主意。对这些元组的计算将涉及加法、乘法、典型的域内容。添加和乘以域的元素？看起来我们希望我们的同态是多项式！而且，事实证明，存在一个像这样的范畴，即代数簇的范畴。一些有限域元素的元组的范畴，你可以通过应用多项式在其中映射事物。因此，我们的公钥空间应该是代数簇范畴中的群对象，通常称为代数群。

我们已经对它们进行了分类。主要有两种类型，线性群和阿贝尔簇。你也可以将它们相乘，但我们真的对单群感兴趣，因此我们希望它们以最基本的形式存在。首先是线性群。它们有两种类型，加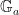法群 和乘法群 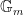。如果不是因为这种非常有效的算法可以解决该群中的离散对数问题，该算法名为“除法”，那么加法群将适用于 Diffie-Hellman。我们将乘法群放在一边，并在下一章中讨论。这让我们只剩下阿贝尔簇。簇有一个重要的不变量，称为维数。那么维数为 1 的阿贝尔簇是什么？椭圆曲线。它们效果很好。我们可以进入更高的维度（事实上，人们已经探索了这一点），但事实证明，除了头痛之外，你什么也得不到。它们会产生安全的结构，但点计数很困难，并且你会得到这些“特殊除数”，这使得恒定时间编程成为一场噩梦，并且没有任何回报。所以这就是椭圆曲线的原因，即使乍一看椭圆曲线看起来像是“群”的一个非常任意和奇怪的选择，但实际上几乎是唯一的选择。

那么有限域 Diffie-Hellman 呢？

这只剩下乘法群。它出现在我们的分类中，你可能知道它已用于密码学（名称为有限域 Diffie-Hellman），那么这篇博客文章的标题不应该是“没有 Diffie-Hellman，只有椭圆曲线 Diffie-Hellman 和有限域 Diffie-Hellman”吗？

我的意思是，是的，但那将是一个糟糕的标题，没有那么吸引眼球，所以让我们通过证明有限域 Diffie-Hellman 也只是椭圆曲线 Diffie-Hellman 来结束这篇博客文章。好吧，“椭圆曲线” Diffie-Hellman，但我有点超前了。

我们在这篇博文中对很多对象进行了分类，那么再分类一个怎么样？我们如何描述所有（直到同构）的椭圆曲线？

为此，我们需要所谓的j 不变量，定义为 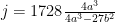，对于由 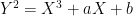给出的椭圆曲线。当且仅当两个椭圆曲线具有相同的 j 不变量时，它们才是同构的（在代数闭包上）。

有多少个 j 不变量？换句话说，基本域的每个元素都出现吗？事实证明，是的。给定一个元素 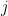，如果 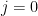，我们可以使用曲线 。对于 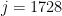，我们可以使用曲线 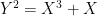。对于所有其他情况，我们可以简单地使用 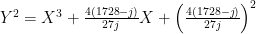。你可以检查一下，这将具有正确的 j 不变量。

换句话说，如果两个椭圆曲线共享相同的 j 不变量，则它们是同构的（在代数闭包上），并且基本域的每个元素都有一个 j 不变量。因此，我们可以将椭圆曲线视为仿射线上的点，并且不知何故，所有椭圆曲线的集合本身的行为就像一个代数簇。（这是一个非常强大的概念，称为模空间）。仿射簇总是让人觉得它们是不完整的，你真的想看看是否可以向其中添加任何无穷远点。特别是，仿射线真的想成为一条射影线，并添加它所欠的一个无穷远点。事实证明，我们可以以一种明智的方式做到这一点（构建 1 属稳定曲线的模）。这个无穷远点？它属于曲线 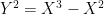。乍一看，它看起来有点像椭圆曲线。当然，它不是 Weierstraß 形式，但你可以纠正这一点并给出具有该形式的同构曲线（我现在太懒了，不想这样做）。但是，这不是椭圆曲线。为了使曲线为椭圆，它不能有任何奇点，而这条曲线有......，好吧，这是它的图：

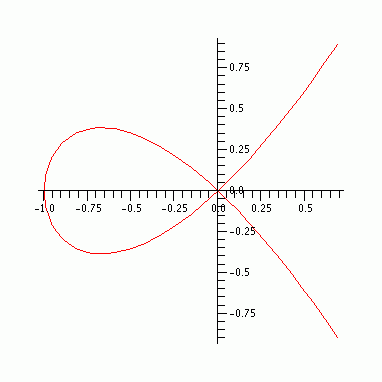
当曲线以这种尴尬的方式自身相交时，那就是一个奇点。但除此之外，它非常好。事实上，你甚至可以使用与椭圆曲线相同的公式来进行点加法等操作，只需远离 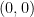处的奇点即可。当你这样做时，你会注意到一些奇怪的事情。你可以简化公式。当通过手动进行代数运算时，它有点长，但很容易做到。当你简化它时，你会注意到节点曲线上的点（除了奇点）可以用单个非零域元素来描述，并且将两个点相加与将相应的域元素相乘相同。换句话说，这条曲线，这条有点尴尬的被拒绝的椭圆曲线，给了我们乘法群。有限域 Diffie-Hellman 也只是椭圆曲线 Diffie-Hellman，只是在一条意外扭曲了一点的曲线上。我们很自然地发现了这条曲线，试图与同一模空间上的椭圆曲线朋友们在一起（而不是具有更令人讨厌的奇点的尖点曲线 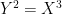，它碰巧给你加法群，并且没有出现在这个模空间上）。

因此，椭圆曲线远非任意性，Diffie-Hellman 从来都不是一个实际的选择。只有椭圆曲线。

• 标签 ellipticcurves, incomprehensible

• 原文链接： keymaterial.net/2025/05/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～