零知识证明 - PLONK算法零知识性问题
- Star Li
- 发布于 2022-07-29 09:48
- 阅读 4527
PLONK的原始论文存在一个零知识性的问题。商t多项式没有添加随机性,导致simulator不能模拟出证明。
前几天,看到PLONK算法作者Ariel Gabizon发了一个Twitter,提到原始PLONK算法的零知识性存在问题:

简单的说,原始论文把商多项式t,直接分成三部分t_lo,t_mid,t_hi,并没有在这三部分多项式添加随机性。这样的话,Simulator(模拟器)不能模拟出这些多项式的承诺。
理解这个问题,先理解一下模拟器:
Formally, what it means for a protocol to be zero-knowledge is defined in terms of a simulator. The simulator is a machine that operates in a different world that is indistinguishable from the real-world for the party that is assessing whether knowledge was leaked. In this world, called the ideal world, the simulator has additional powers that allows it to compute a proof without knowing anything besides the truth of the statement.模拟器(simulator)用来证明零知识性的。Simulator和现实世界不一样,拥有除了witness外的其他所有知识。如果Simuator能构建能被验证者验证的证明,说明一个证明能在没有witness信息的情况下构建。反过来说,如果Simulator能“模拟”出一个正确的证明,则该证明系统是零知识的。
体会Simuator,可以再看看Groth16算法的Simulator:

在不提供witness的情况下,随机出A/B,可以通过公开输入信息以及trusted setup的信息计算出C,从而构建正确的证明。
理解了Simulator,再看PLONK原始论文的零知识性。因为t_lo,t_mid,t_hi并没有添加随机性,Simulator为了构造这些多项式的Commitment,必须通过商t多项式计算。要构造商t多项式,需要witness信息。所以说,PLONK原始论文中的算法不能构造相应的Simulator。进一步说,因为原始PLONK算法不具备零知识性,witness有可能泄漏。
Ariel Gabizon也在Twitter中给出了更新后(添加了随机性)的t_lo,t_mid,t_hi的计算方法,并强调调整后算法的Simulator也会补上。
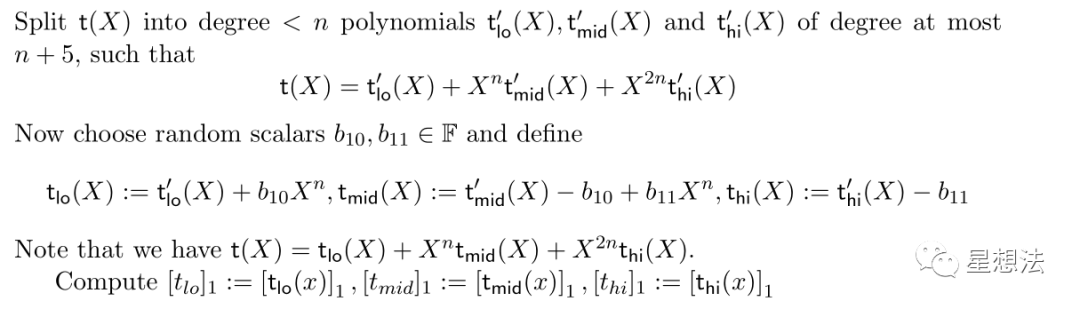
总结:
PLONK的原始论文存在一个零知识性的问题。商t多项式没有添加随机性,导致simulator不能模拟出证明。

- ZK编年史:哈希登场 144 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 358 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 285 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 370 浏览
- Zcash:比特币遗忘的隐私 432 浏览
- ZK编年史:计算模型 301 浏览
- lambdaworks 2026 年更新路线图和优先级 364 浏览
- 2026年构建机构级DeFi平台真正需要什么 904 浏览
- zkMesh:2026年1月回顾 449 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 643 浏览
- Zcash 的时代到来了 778 浏览
- ZK 编年史:电路(第二部分) 422 浏览

