Uniswap v3 流动性数学 [翻译]
- Antalpha Labs
- 发布于 2024-02-28 17:03
- 阅读 5785
为 Uniswap v3 流动性数学提供进一步阐释
本文翻译自:https://atiselsts.github.io/pdfs/uniswap-v3-liquidity-math.pdf
1.前言
Uniswap v3 作为 Uniswap 协议的最新版本,引入了集中流动性等许多新功能。它允许流动性提供者将其流动性集中在特定的价格范围内,从而提高资本效率。然而,头寸的流动性、资产数量及其价格范围之间的数学关系变得较为复杂。Uniswap v3 白皮书定义了流动性数学的核心概念,然而其提供的信息十分简洁,与 Uniswap 用户和开发人员提出的问题之间存在差距,例如:
-
给定头寸的总流动性和价格范围,该头寸在特定价格 $P$ 下拥有多少资产 $X$ 和资产 $Y$ ?
-
给定价格范围、当前价格 $P$ 和资产 $X$ 的数量 $x$ ,应向其供应多少资产 $Y$ 以涵盖这个价格范围?
-
给定要存入流动性池的 $x$ 数量的资产 $X$ 和 $y$ 数量的资产 $Y$ ,以及当前价格 $P$ 和预期价格范围的下限,预期价格范围的上限是多少?
本文旨在弥合这一差距,为 Uniswap v3 流动性数学提供进一步阐释。
2.计算
2.1 计算流动性和资产数量
白皮书中的方程 6.5 和 6.6 似乎给出了计算 $L$ , $x$ 和 $y$ 的简单方法:
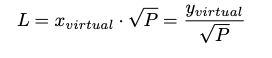
但是,这里的 $x$ 和 $y$ 是代币的虚拟数量,而不是真实数量。计算实际数量 $x$ 和 $y$ 的数学公式在白皮书的最后给出,具体见方程 6.29 和 6.30。
这些方程可以从白皮书中的关键方程 2.2 推导出来:
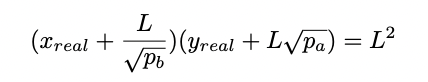
尝试直接解方程 2.2 以得到 $L$ 的结果会得到一个非常复杂的答案。相反,我们可以注意到在价格范围之外,流动性完全由单一资产提供,要么是 $X$ ,要么是 $Y$ ,具体取决于当前价格在价格范围的哪一侧。我们有以下三个选择:
- 假设 $P ≤ p_a$ ,流动性的 position 完全由代币构成,因此 $y = 0$ :
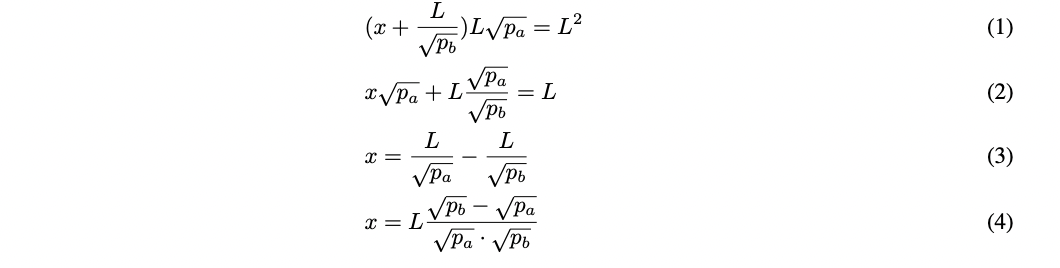
该头寸的流动性为:
- 假设 $P ≥ p_b$ ,流动性的 position 同样完全由代币构成,因此 $x = 0$ :
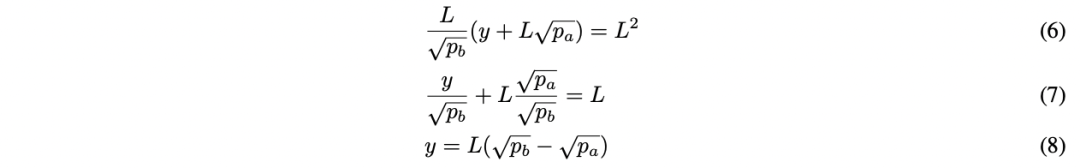
该头寸的流动性为:
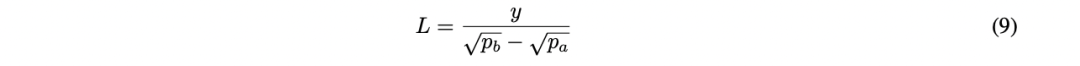
当前价格位于范围内: $p_a < P < p_b$ 。理解这一点的方式是考虑在最优位置,两种资产将平等地贡献流动性。换句话说,在范围的一侧 $(P,p_b)$ 由资产 $x$ 提供的流动性 $Lx$ 必须等于在范围的另一侧 $(p_a,P)$ 由资产 $y$ 提供的流动性 $Ly$ 。
根据方程 (5) 和 (9),可以得到如何计算单资产范围的流动性。当 $P$ 位于范围 $(p_a,p_b)$ 时,我们可以将 $(P,p_b)$ 视为 $X$ 提供流动性的子范围,将 $(p_a,P)$ 视为 $Y$ 提供流动性的子范围。将此代入方程 (5) 和 (9),并令 $Lx (P,p_b) = Ly (p_a,P)$ ,可以得到:
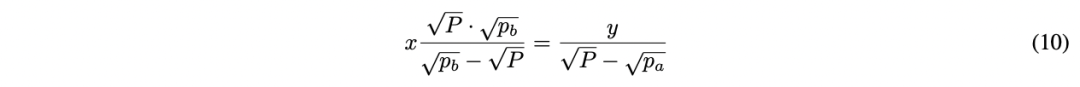
方程式 (10) 非常重要,因为它可以解出 $x$ 、 $y$ 、 $P$ 、 $p_a$ 、 $p_b$ 中的任意一项,而无需参考流动性。然而,对于 $x$ 和 $y$ 来说,这并非必要;简单修改方程 (4) 和 (8) 就足够了:
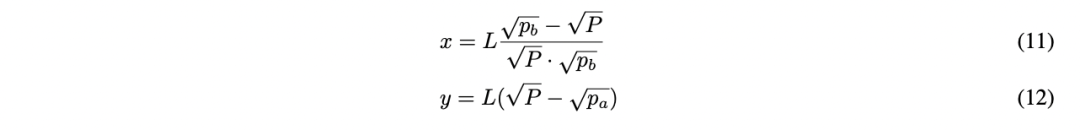
总结:
-
如果 $P ≤ p_a$ ,则 $y = 0$ ,而 $x$ 可以通过方程 (4) 计算。
-
如果 $P ≥ p_b$ ,则 $x = 0$ ,而 $y$ 可以通过方程 (8) 计算。
-
否则,当 $p_a < P < p_b$ 时, $x$ 和 $y$ 可以分别通过方程 (11) 和 (12) 计算。
从概念上讲,这个结果只是以稍微不同的形式重新陈述了白皮书中的方程 6.29 和 6.30。然而,白皮书中对 $∆$ 的使用可能会对新用户造成困惑 —— $∆$ 的差异是什么?如果这是一个全新的头寸呢?为保持简单,方程 (4) - (12) 避免了以上提及的任何差异。当然,深入研究时可以明确,白皮书中的方程 6.29 和 6.30 甚至适用于新头寸:在这种情况下,我们只需要将 $∆L = L$ 。
2.2 根据资产数量计算价格范围
2.2.1 价格范围边界
在给定资产数量和当前价格 $P$ 的情况下,不可能同时推断出两个边界 $p_a$ 和 $p_b$ 。因为只有一个方程(方程(10)),因此当存在两个未知变量时,结果是不确定的。对于任何给定的资产比例,都存在无穷多个相应的价格范围。
然而,以下问题可以解决:
-
$P, x, y$ 和 $p_a$ 已知; $p_b$ 的值是多少?
-
$P, x, y$ 和 $p_b$ 已知; $p_a$ 的值是多少?
-
$P, x$ 和 $y$ 已知;如果价格从当前价格增加 z%,则价格将达到 $p_b$ 。 $p_a$ 对应的价格下跌百分比是多少?换句话说,给定 $p_b/P$ 的比率, $p_a/P$ 是多少?
计算这些答案的一种方法是首先计算价格一侧的流动性。这里开始,我们假设价格在一个非空的范围内,并且不等于范围的端点;形式上, $p_a < P < p_b$ 。一旦 $L$ 已知,就可以分别使用方程 (12) 和 (11) 计算 $p_a$ 和 $p_b$ 。使用平方根能极大简化解,使用起来更方便计算。
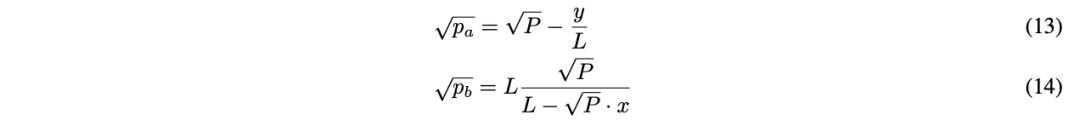
或者,可以跳过流动性计算,直接解方程 (10) 得到 $p_a$ 和 $p_b$ 的平方根:
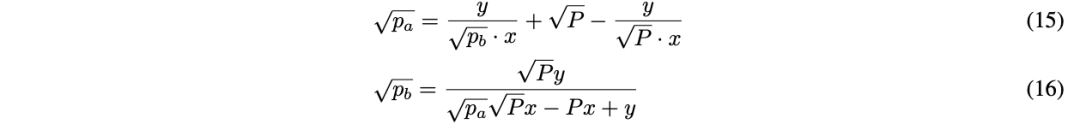
2.2.2 价格区间比例
用户还可以根据当前价格的增加或减少来考虑价格范围。我们引入新的符号 $c$ 和 $d$ 来 表示,令 $c^{2}\cdot P$ 等于范围的上限, $d^{2}\cdot P$ 等于下界:
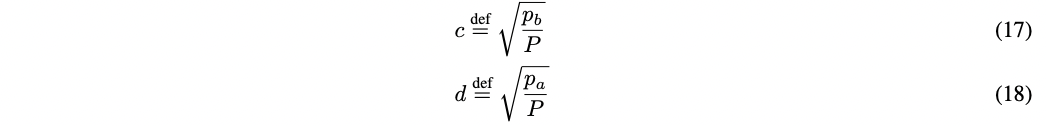
显然可以得到以下内容:
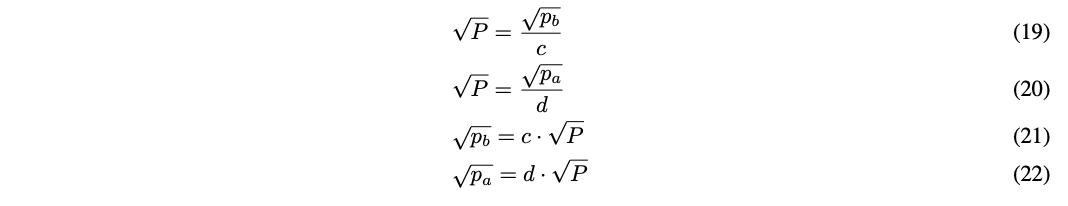
现在可以使用方程 (10) 来表示它们之间的相互关系。
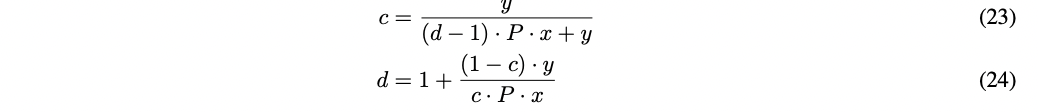
现在,例如已知 $p_a$ 对应于当前价格的 70%( $c^2$ 等于 70% = 0.7),可以通过使用方程 (24) 计算 $d^2$ 来计算对应于 $p_b$ 的当前价格的百分比。
3 应用
3.1 实施细节
在将这些数学应用于源代码时,请注意以下几个方面:
-
Ticks: Uniswap 中的价格范围具有称为 tick 的离散边界。第 i 个 tick 的价格定义为 $p(i) = 1.0001^i$ 。只有与初始化的 tick 对应的特定价格点可以作为价格范围的边界。
-
刻度间隔: 并非所有刻度都可以初始化。可以索引的确切刻度索引取决于池的费用水平。1% 的池具有最宽的刻度间隔,为 200 个刻度,0.3% 的池为 60 个刻度,0.05% 的池最小,为 10 个刻度。
-
Fixed point math: Uniswap v3 使用 fixed point math。这是因为 Solidity 不支持浮点数,而且定点数学有助于最小化舍入误差。这种数学带来了新的挑战,例如需要将带有定点基数的数字相乘或相除以保持其正确的范围。
-
Decimal: ERC20 代币定义了一个称为
decimal的字段。在以太坊生态系统内部,加密货币的数量以整数表示。为了将 ERC20 代币的数量从这种内部表示转换为人类可读的值,需要除以 $10^{decimal}$ 。不同的 ERC20 合同为其代币定义了不同数量的小数点;例如,DAI 的 decimal 为 18,而 USDC 有 6 个。1 USDC 的人类可读价格约为 1 DAI;但从流动性计算的角度来看,1 USDC 相对于 DAI 的价格约为 $10^{(18-6)} = 10^{12}$ 。
3.2 没有实施细节的示例
在这个示例子节中,为了增加解释的清晰度,我们忽略了上面提到的实施细节。请注意,与从 Uniswap 代码和 UI 获得的结果相比,这可能导致小的数值误差。
3.2.1 示例 1:从给定价格范围计算资产金额
问题:一个用户拥有 x = 2 ETH,并希望在 ETH/USDC 池中建立一个流动性仓位。ETH 的当前价格为 $P$ = 2000 USDC,目标价格范围为 $p_a$ = 1500 到 $p_b$ = 2500 USDC。他们需要多少 USDC( $y$ )?
解决方案:首先,使用方程 (5) 计算范围顶半部分的流动性(将 $p_a$ 替换为 $P$ 以获得顶半部分):
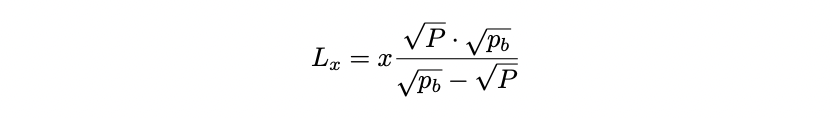
然后,使用 $L$ 的值通过方程 (8) 计算 $y$ :
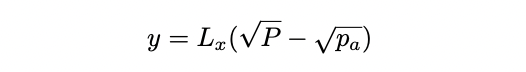
答案是 $y$ = 5076.10 USDC。
3.2.2 示例 2:从给定资产金额计算范围
问题:用户有 x = 2 ETH 和 y = 4000 USDC,并希望使用每 ETH $p_b$ = 3000 USDC 作为流动性提供上界。为确保已开仓位使用其全部资金,做市范围的下界( $p_a$ )是多少?
解决方案:可以使用与上述示例 1 中相同的半范围技巧计算头寸的流动性,然后计算做市范围的下界。然而, $p_a$ 也可以通过方程 (15) 直接计算:
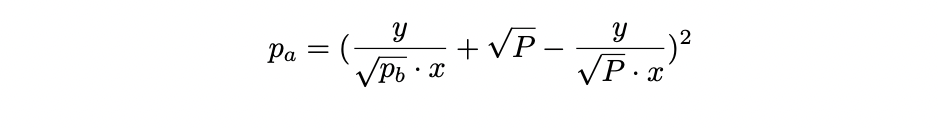
答案是 $p_a$ = 1333.33 USDC。较低的价格是当前价格的三分之二,而当前价格是较高价格的三分之二:这是因为 USDC 和 ETH 的初始值相等。
3.2.3 示例 3:价格变动后的资产
问题:使用示例 2 中创建的流动性头寸,当价格变为 $P$ = 2500USDC/ETH 时,资产余额是多少?
解决方案:首先计算头寸的流动性,使用之前计算出的 $p_a$ = 1333.33:
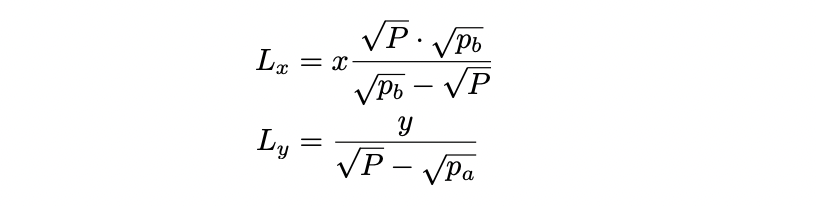
使用 64 位浮点数运算,结果分别为 $Lx$ = 487.41718030204123 和 $Ly$ = 487. 4144693682443。 $L$ 是这两者中的最小值: $L = min (Lx, Ly)$ ,在这种情况下对应于 $Lx$ 。
现在,设 $P'$ = 2500,我们可以使用方程 (4) 和 (8) 找到 $x'$ 和 $y'$ :
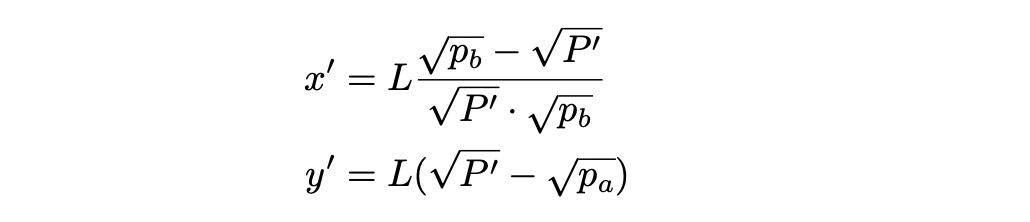
答案是 $x$ = 0.85 ETH 和 $y$ = 6572.89 USDC。可以从这个结果计算出无常损失。
我们也可以使用白皮书提供的 delta 计算,即方程 6.14 和 6.16,来计算这个答案:
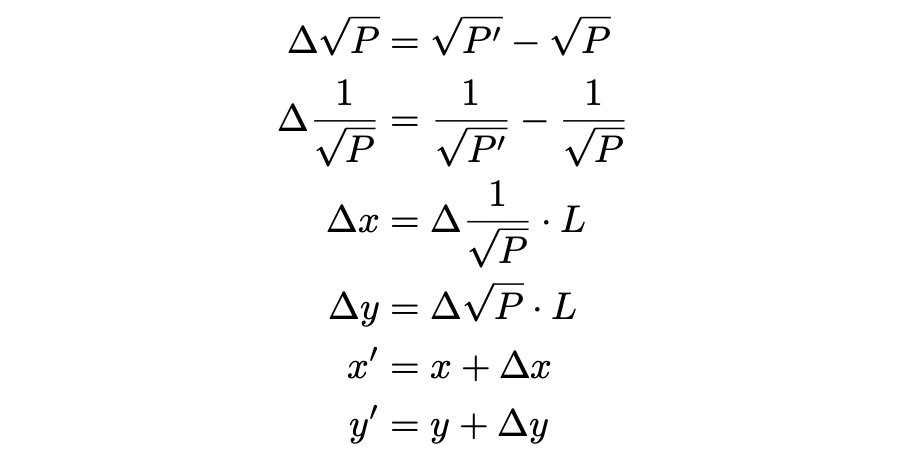
变动值为: $∆x$ = −1.15 ETH 和 $∆y$ = +2572.89 USDC。
3.3 包含刻度数学和价格转换的示例
刻度数学是解释 Uniswap v3 API 提供的值和 Uniswap v3 子图中索引的数据所必需的。首先,让我们简要回顾一下白皮书中的刻度数学。Uniswap v3 将所有可能价格的连续空间映射到由刻度索引的离散子集。刻度与价格之间的唯一关系由刻度基本参数定义,在 Uniswap 中等于 1.0001。第 i 个刻度对应的价格是:
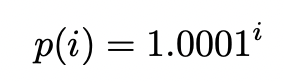
这表明:
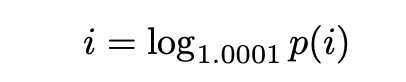
在使用价格的平方根进行计算时:
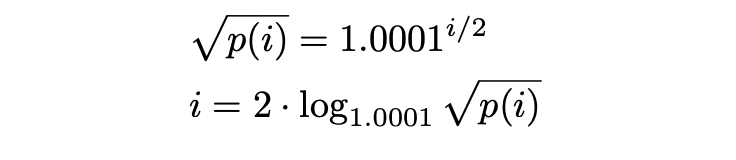
3.3.2 将价格转换为人类可读的形式
在内部,价格只是 $y$ 和 $x$ 之间的关系。然而,为了在用户界面中显示它,必须考虑资产 $X$ 和 $Y$ 的小数位数。让我们分析一个 Uniswap v3 NFT 来证明这一点,以 ID 为 600006 的 NFT 为例。如图 1 所示,这个 NFT 的「Min Tick」为 200240, “Max Tick”等于200700。将这些刻度数转换为价格,我们得到以下价格范围:
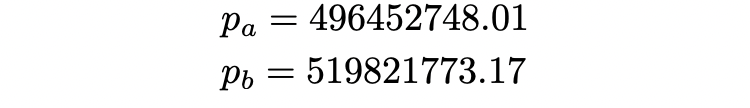
问题在于 USDC(第一个资产 $X$ )只有小数位数 decimalsx = 6,而 wrapped ETH(第二个资产 $Y$ )有小数位数 decimals = 18。由于价格是 $y/x$ ,不带小数的价格等于:
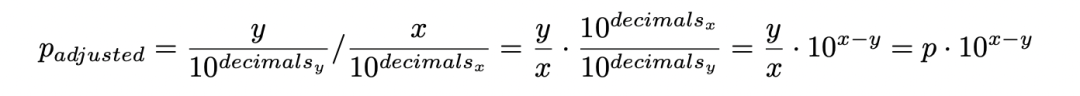
在示例池中:
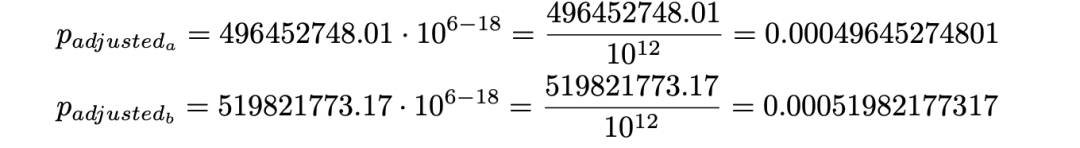

这些表示了以 ETH 为单位的 USDC 的价格。要以 USDC 为单位获取 ETH,需要反转价格:
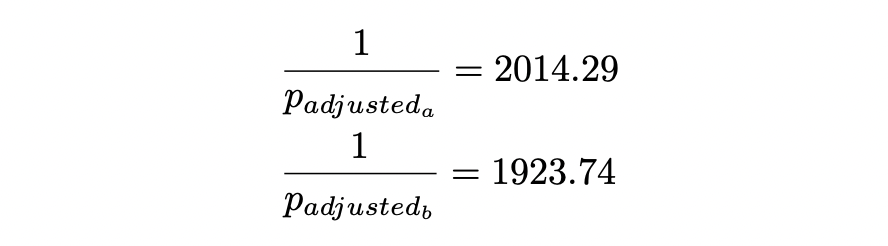
请注意,最后一个范围是反转的,反转价格在顶部刻度处低于底部刻度处的反转价格。
3.3.3 当前刻度范围内资产的数量
为了了解价格范围内的资产数量,首先我们必须得到池的流动性。一个池变量跟踪特定的刻度范围内的流动性。Uniswap v2 只要不向池中添加或删除资产,池的流动性就保持不变,而与 v2 不同的是, Uniswap v3 中的池流动性可能会在价格跨越价格变动范围边界时发生变化。特别是在跨越具有非零流动性净值的刻度边界时会发生变化。

在本文中,该查询返回的 $L$ 为 22402462192838616433,刻度为 195574,对应价格为 3211.84 USDC/ETH。
池的价格变动间隔由其费率决定。对于 0.3% 的池,刻度间距等于 60。这意味着 只能初始化可被 60 整除的刻度。最接近具有此属性的返回值的刻度是:
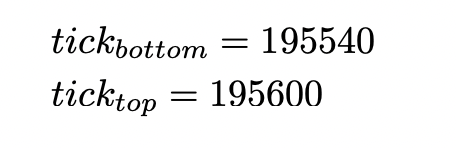
因此,价格范围为:
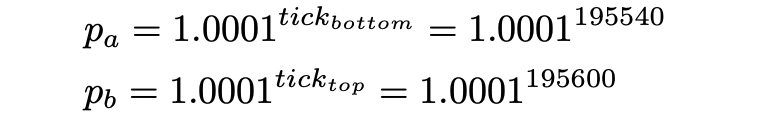
使用方程 (11) 和 (12) 来计算可以从当前价格范围内的流动性中获取的 USDC 或 ETH 的最大值:
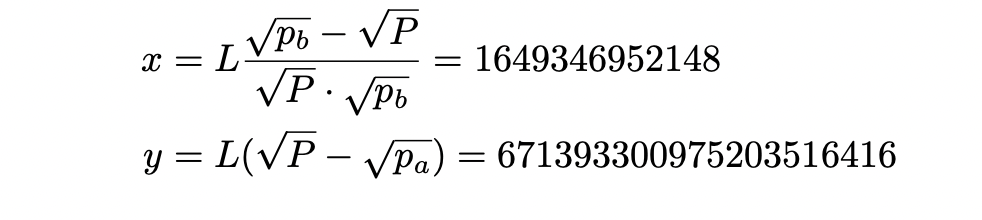
在调整各代币的小数后:
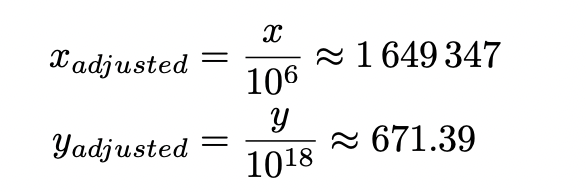
大约有 165 万 USDC 和 671 ETH 被锁定在当前的价格范围内。这意味着购买 165 万 USDC 的人将当前价格移动到当前价格范围的一端。相反,如果有人购买 671 ETH,那将把价格移动到范围的另一端。
- 转载
- 学分: 15
- 分类: Uniswap
- 标签: DeFi Uniswap V3
- 从 DeFi 到 NeoFi :下一个篇章 95 浏览
- 你的DeFi协议需要吸引机构注意力的5个架构转变 282 浏览
- 来自 Tomasz 的更新 210 浏览
- 将结构化收益引入 Neutrl NUSD 79 浏览
- “夺旗”竞赛继续! 270 浏览
- AI 正热,加密货币遇冷,那又如何? 491 浏览
- Polymarket交易手册 453 浏览
- 如何在稳定币上获得收益 290 浏览
- DeFi中的移动平均线:安全漏洞与攻击预防 212 浏览
- 《Uniswap V3 开发指南》上线,一本把 Uniswap V3 讲“透”的电子书 389 浏览
- MegaETH主网已上线:应用、社区以及为什么这个L2感觉与众不同 280 浏览
- $PUMP 论点:一月份的赌场 344 浏览

