密码学入门：多项式

这是关于密码学的更大系列文章的一部分。如果这是你第一次接触这篇文章，我强烈建议你从 系列的开头 开始。

到目前为止，在这个系列中，我们已经投入大量精力进一步理解 椭圆曲线密码学 (ECC)。我们稍微偏离了一下，介绍了 哈希函数 [https://learnblockchain.cn/article/10758]，但这就是我们从核心主题偏离的程度。

虽然ECC非常丰富且强大，但密码学远不止于此。在这一部分，我想向你介绍神奇的 多项式 世界。

我们可以用多项式做一些椭圆曲线无法实现的事情。那么就让我们开始呈现它们，然后来看看它们的应用。开始吧！

多项式

你或许在高中期间见过这些家伙。从本质上讲，它们非常简单：它们由涉及 变量 的表达式组成，这些变量只能被 加、减 和 乘。乘法还意味着我们可以有变量的 幂。每个求和中的项都可以与一个称为 系数 的数字相乘。所以，像这样：

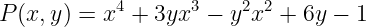
注意，一个多项式可以有 多个不同的变量。在这方面没有限制——但在大多数情况下，我们只会使用一个变量，并将其表示为 x。

作为一种好奇，两个多项式的相加会产生另一个多项式，而两个多项式的相乘也会产生另一个多项式；正因为如此，所有多项式的集合形成了一个被称为 环 的数学对象。

再说一次？不是那个环，伙计！

多项式在数学的多个领域都有应用。它们在密码学中也很有用，但有一个 条件：我们必须在 所有 位置使用整数。这意味着变量只能被赋予 整数值，我们不能有像 0.5 这样的系数多项式。这保证了多项式将 仅 输出整数。

此外，在密码学中，我们在 模运算 下工作。因此，多项式的完整表达，如果你愿意，那将看起来像这样：

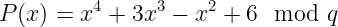
最后，多项式的 度 由变量的最高幂定义。例如，我们刚才看到的多项式的度为 4。

通常，当人们开始问自己 “ 我为什么需要了解这个？” 时，这就是起点。

是的，我知道。我保证这些应用会是 非常有趣的。请耐心等待，因为我们还需要介绍一种特定类型的多项式，它对我们来说将是极其有用的： 拉格朗日多项式。

插值

你有没有注意到，只有一条 唯一的 直线经过 两个点？

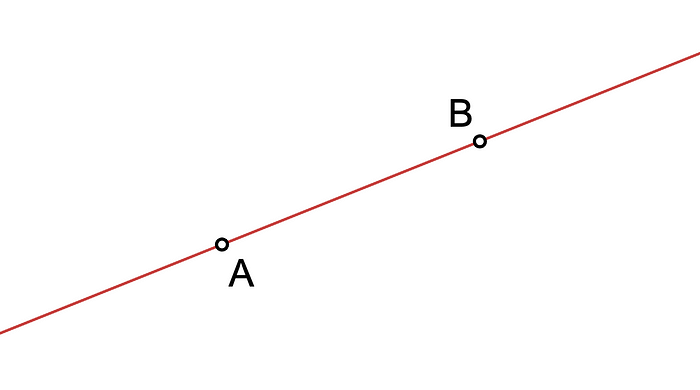
无论你怎么努力，都没有 其他的直线 能够通过 A 和 B。而直线实际上就是一个 多项式函数， P(x) = m.x + n。而这 不是巧合。

现在让我们尝试三个点。它们可以是 对齐的，在这种情况下你可以通过它们画一条线，或者不对齐。在后一种情况下，你可以画 一条，并且 仅有一条 抛物线（一个 二次 多项式）通过它们。

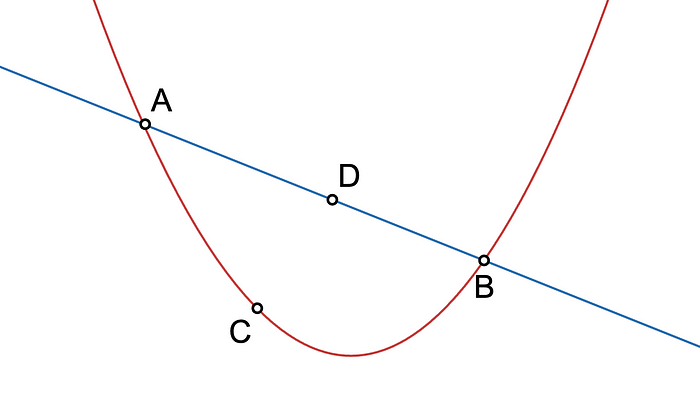
需要澄清的是，由于我们使用整数和模运算，曲线只是可视化所发生事情的一种方式——但我们实际上使用的是离散点。

一般来说，对于给定的一组 m 点，存在一个 唯一的 多项式，最高度为 m - 1，它通过所有的 m 点。这个多项式是非常特殊的——如此特殊，以至于它有自己的名称： 拉格朗日多项式。我们说它对 m 点进行 插值。

是什么让它如此特别？为了理解这一点，让我们做一个小练习：

取任意三个整数值点（(x₁, y₁)、(x₂, y₂) 和 (x₃, y₃)）。我们知道一条 抛物线 会插值这三个点，所以我们的拉格朗日多项式看起来是这样的：

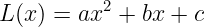
我们仍然不知道 如何 计算插值多项式，但这暂时没问题。现在，取一堆 x 值，并为每个值计算 L(x)——我们得到了很多 属于同一抛物线 的点。

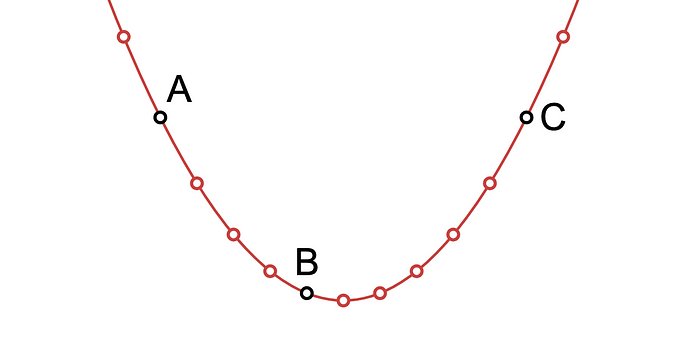
抛物线上的点

而这里的好处在于：从上面图中取的任何一组三个或更多的点产生的都是 相同的插值多项式。

你可能仍在想，“好吧，但我为什么需要知道这些东西??？”

好吧，好吧。你说得对。够多的理论了。让我们看看一个应用是怎样的，在我失去你兴趣之前！来了。

数据丢失编码

每当你通过消息应用发送视频时，你希望接收方能够以 一个完整的、未更改的 片段 收到，对吧？但缩放一下，这并不是 信息传输 的真实情况。你并不是通过互联网发送单个信息包，就像从亚马逊买的包裹。

如果它能简单，那多好啊

实际上，原始视频是以 小块 发送的，这些小块称为 信息包。在你的设备、接收方的设备以及两者之间的许多地方，都有正在运行的过程（你好，TCP），确保每个包都到达其目的地，同时还处理从其碎片中重构原始视频的繁琐过程。

而在它们旅行的过程中，许多时候，信息包会被 丢失 或遭到 破损。是的，你没听错。我们提到的过程通过重新请求任何丢失的包来缓解这一复杂性。

但还有另一种解决这个问题的方法：在我们的数据中引入 冗余。

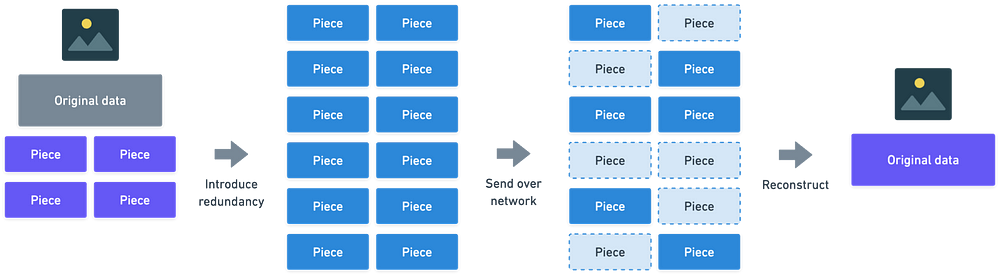
即使有一些信息包丢失，我们仍然可以重建数据

冗余 意味着我们实际上要发送比实际需要更多的信息。想象一下，我们的视频分为四个小块信息——那么我们将发送比四个要大的块数量。即使途中信息丢失，接收者 仍然能够重建原始数据。

但如何？

多项式，这就是方法！

是的，科学！

像往常一样，一切都从一个简单的想法开始：原始 数据块 可以是多项式的 系数！

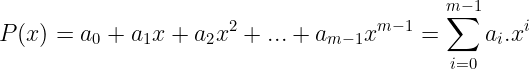
每个数据块只是一个 二进制 数字，也就是一个 整数。并且要记住，我们可以从至少 m 个点重构一个度为 m - 1 的多项式（通过拉格朗日插值）。你怎么看这个继续进行？

我们只需要在 k 个不同的点 x 处评估 P(x)，并且我们要求 k 大于 m。你问还有多少？这取决于你期望 丢失 的包数量，因为点 (x, P(x)) 实际上就是要发送到网络上的 信息包。

当然，接收者可以通过插值使用 k 个点中的任何 m 个重构原始多项式，并通过恢复 系数，他们有效地 重建 原始消息！

这种技术被称为 Reed-Solomon 错误纠正编码。它的一个很酷的应用是在 深空通信 中，当数据在广阔的距离上发送时，会发生错误和数据损坏。很棒，对吧？

插值，重访

现在我们知道了至少一个拉格朗日多项式的应用。但我们仍然不知道 如何进行插值。

找到多项式插值的 标准或直接方法 实际上非常麻烦。你会找到这样的表达式：

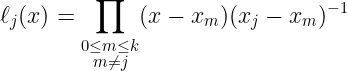
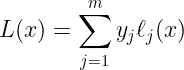
我的意思是，我们可以处理这些方程，没问题——但问题是，这实际上并不是最 高效 的插值方法。

对于那些知道大O符号的人来说，直接插值的复杂度是 O(n²)。而今天已知的最高效的算法，以下所示，复杂度是 O(n.log(n))。

插值的最佳和最快的方法是使用 快速傅里叶变换 算法（简称FFT）。我们不会详细讨论它是如何工作的，因为它涉及一些我们还没有介绍的概念，如群的 单位根。

然而，外面有 很好的资源 如果你有兴趣深入剖析算法的内部。如果这是你的菜，尽情享受吧！

秘密分享

最后，让我们看看另一个应用，它将非常有助于设计更为熟悉的协议，如签名。让我们看看 夏密尔秘密分享。

你还记得 Diffie-Hellman 密钥交换 是如何允许多个方生成共享秘密的吗？好吧，它有一个限制：秘密是 生成的。

这意味着如果我，Frank，想向一群人披露一个 特定的 秘密值，那么Diffie-Hellman 不适合 这个任务。我们必须考虑另一种策略。

同样，多项式拯救了我们。这是方法：

• 将秘密值 s 设置为 独立项（未与 x 相乘的系数）。
• 然后，选择 m 个随机数作为多项式 P(x) 的系数。
• 最后，选择 k 个 x 值，并在所有这些值上评估 y = P(x)。

你最终会得到一堆点 (x, y)。正如你所知，任何 m + 1 这些点都可以用于 重构 原始多项式 P(x)。

那现在怎么办？假设我与网络中的参与者进行通信。我与Alice共享 (x₁, y₁)，然后与Bob共享 (x₂, y₂)，与Charlie共享 (x₃, y₃)，依此类推。然后他们开始互相交流——Alice向Bob发送 (x₁, y₁)，Charlie发送 (x₃, y₃) 给Alice，等等。

发生的情况是，在某个时刻，Alice 会拥有 足够的片段去 重构 多项式 P(x)。这很好，因为然后她查看 独立项，这恰好就是我想分享的秘密！

这就是广泛称为多方计算（MPC）的一组技术示例。这是一个非常有趣的话题，我们将在未来的文章中扩展讨论。

总结

椭圆曲线、哈希、多项式——我们的工具集不断壮大！随着我们积累更多工具，新的密码学技术为我们提供了。特别是，我们可以将 签名 和 多项式 结合起来，产生一个有趣的新构造： 门限签名。我们将在 下一篇文章 中详细讨论，利用我们当前工具的极限可能性。

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～