手动实现数论变换算法

NTT（数论变换）算法将有限域中的多项式从系数形式转换为点形式。

如果一个多项式具有 阶数，那么我们在 -th 个单位根上对其进行求值，其中

我们不是在 -th 个单位根的集合 中的每个点上评估多项式 ，而是使用多值函数的像保持定理来评估多值函数，该函数通过在 定义域 上用 替换 中的 来创建。然后，我们迭代地将平方根的求值从 扩展到 到 ，依此类推，直到求值扩展到 -th 个单位根。

该方法的运行时间为 。

在第 4 个单位根上评估

首先，我们对函数进行因式分解，以最大化 出现的次数，因为 和 在单位根上很容易求值（它仅导致 ，具体取决于单位根的幂是偶数还是奇数）。

这将创建以下函数：

接下来，我们变换 ，使得 ，这给了我们

这是平方根展开图：

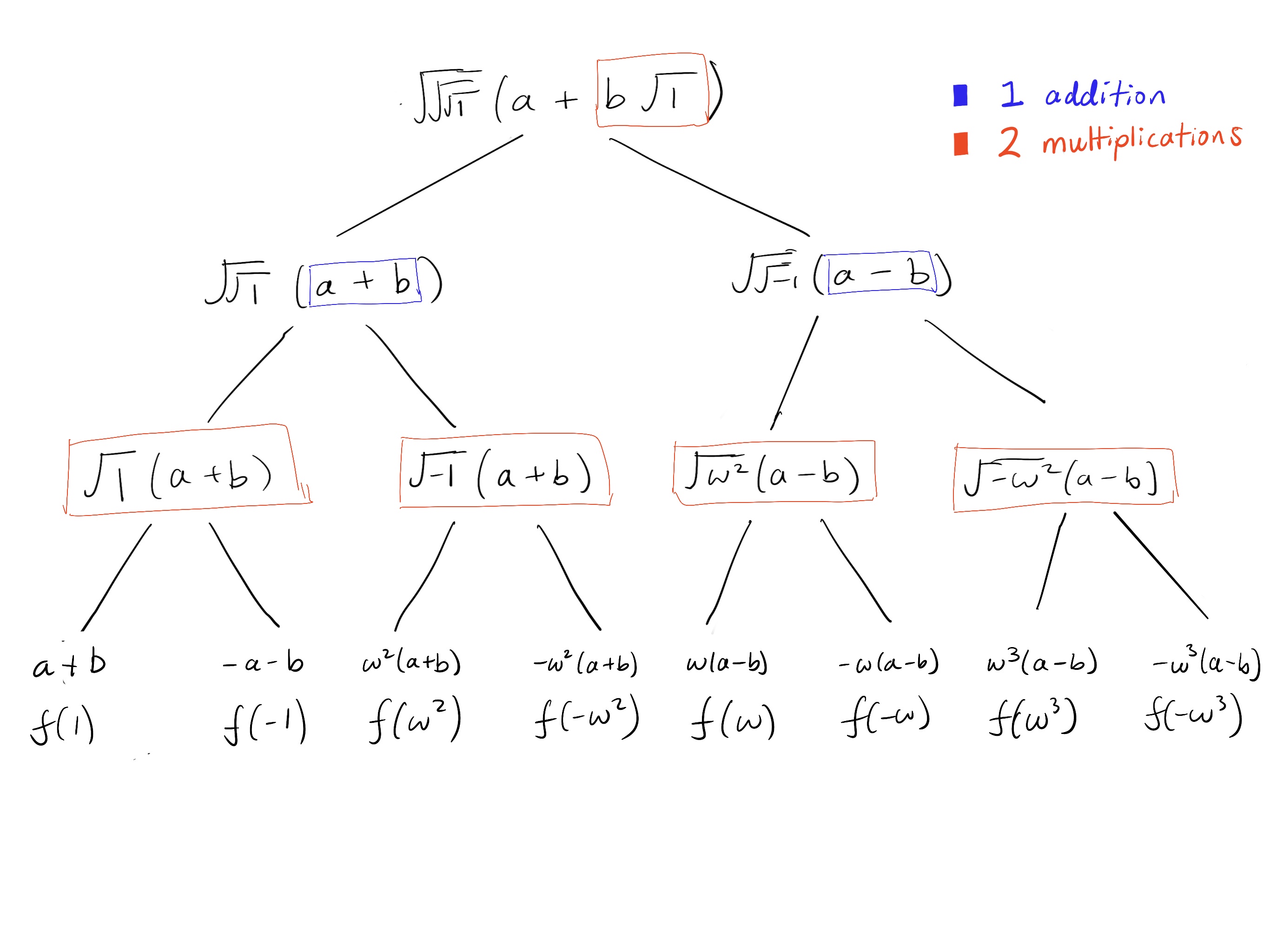
现在，我们将结果与在第 4 个单位根上逐个评估 进行比较：

我们有 和 和 。通过替换，我们有：

练习： 使用上述方法在第 4 个单位根上评估 。提示：使用上面的示例并设置 。

树的高度为 ，我们在每一行上执行 操作，因此运行时间为 。

在第 8 个单位根上评估

首先，我们重新排列多项式以最大化 项的数量（因为 k = 8）。这给了我们：

现在我们替换 得到我们的多值函数

由于在一个图像中绘制评估树会非常大，因此我们将绘制树的左侧，我们在该左侧评估 ，并首先显示该图：

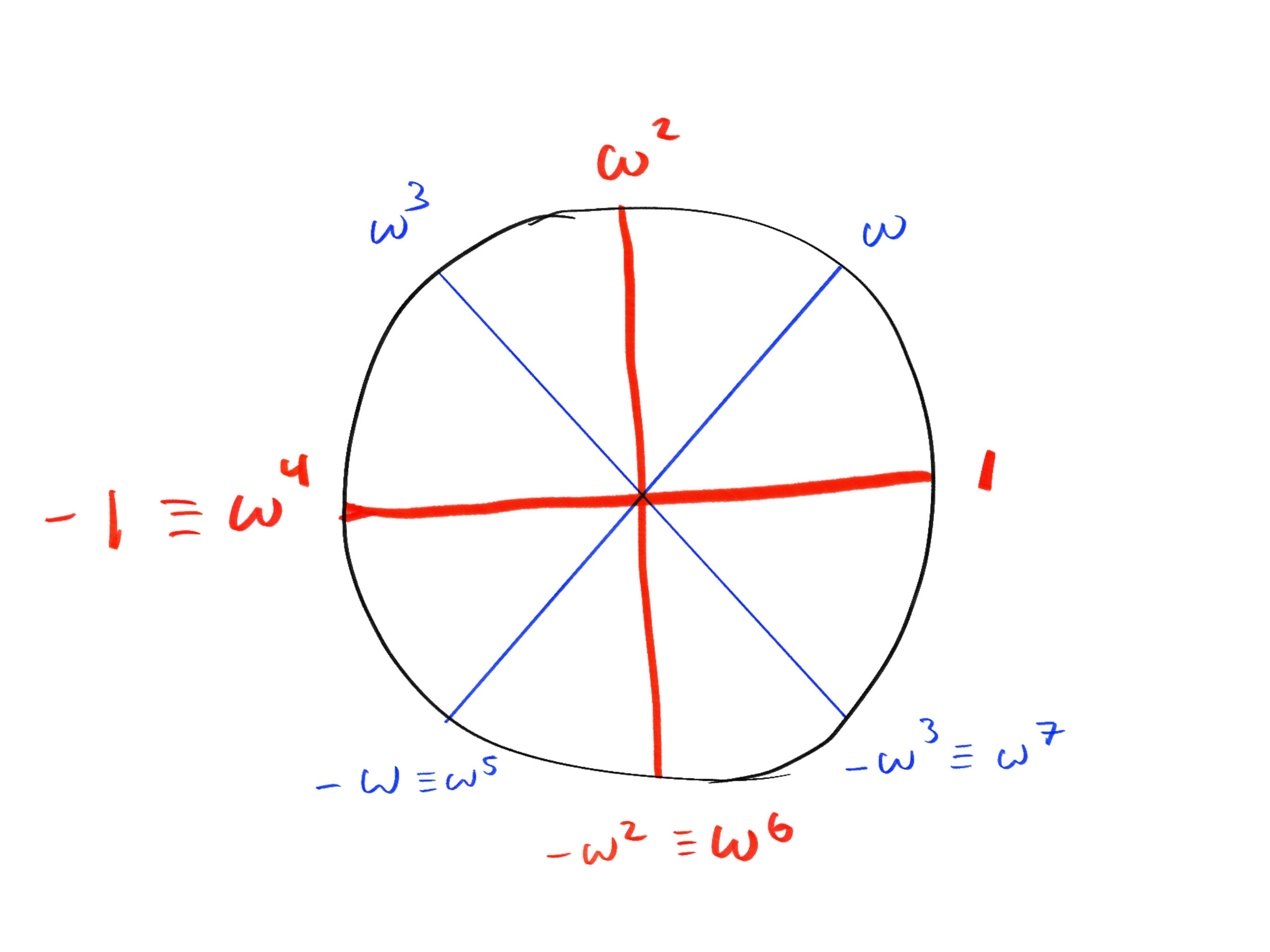
从上图可以看出，

现在我们展开树的右侧，其中 ：

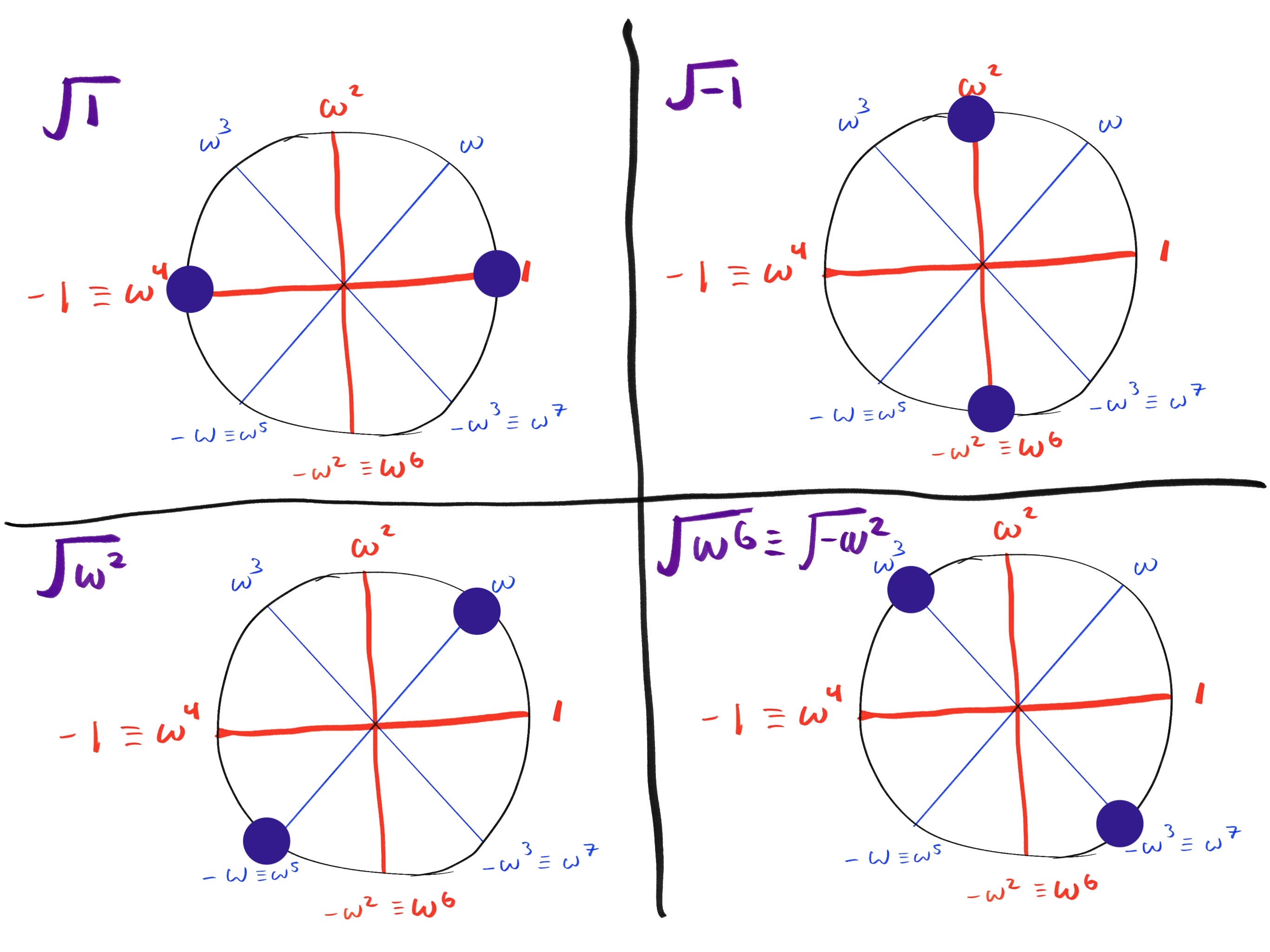
从该结果中，我们有：

将评估结果组合并分配 omega 项，我们有：

接下来，我们按升序排列系数：

现在让我们重新排列评估，从 ， ，…，

如果我们将其与第 8 个单位根的 Vandermonde 矩阵 进行比较，我们可以看到我们正确地计算了 的幂。

Vandermonde 矩阵计算

上面的 Vandermonde 矩阵的推导如下。对于 上的 ，每一行都是 的幂

接下来，我们将 8 的倍数分解出来：

删除 8 的因子，我们得到：

在替换 , , , 之后，我们得到原始的 Vandermonde 矩阵：

练习： 在第 8 个单位根上评估 。同样，请注意你可以设置 。

练习： 在 中评估第 4 个单位根上的 ，其中 。使用 Python 查找原始的第 4 个单位根作为起点。

总结

使用平方根展开在 -th 个单位根上评估多项式，与一次一个地在单位根上评估多项式具有相同的评估结果。这成立的原因是多值函数的像保持定理，因为我们只是在域 上评估多值函数 。

此方法节省了计算成本，因为在每个步骤中，一半的平方根被评估并且乘以它们配对的系数或系数之和。对于其余的评估，结果只是简单地复制下来，而不是重新评估。

• 原文链接： rareskills.io/post/ntt-b...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～