理解PLONK
- Vitalik Buterin
- 发布于 2019-09-24 18:13
- 阅读 1677
文章详细介绍了PLONK零知识证明协议的原理和实现,包括其通用和可更新的可信设置、多项式承诺的使用以及如何将程序转换为多项式方程进行验证。
理解 PLONK
特别感谢 Justin Drake, Karl Floersch, Hsiao-wei Wang, Barry Whitehat, Dankrad Feist, Kobi Gurkan 和 Zac Williamson 的审阅。
最近,Ariel Gabizon、Zac Williamson 和 Oana Ciobotaru 宣布了一种新的通用零知识证明方案,称为 PLONK,其名称是"Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge"(关于拉格朗日基的普遍非交互知识论证的排列的笨重半回文)。尽管针对通用 零知识证明 协议的 改进 已经有 多年的发展,但 PLONK(以及更早的但更复杂的 SONIC 和更近期的 Marlin)所带来的几个增强功能可能会大大改善这类证明的可用性和进展。
第一个改进是,尽管 PLONK 仍然需要类似于 Zcash 中的 SNARKs 的可信设置程序,但它是一个“通用和可更新的”可信设置。这意味着两件事:首先,不必为每个想要证明的程序单独进行一套可信设置,而是在整个方案进行一次单一可信设置后,可以使用该方案与任何程序(最多某个最大大小,由设置时选择)一起使用。其次,多个参与方可以参与可信设置,确保只要其中任何一方诚实,则过程是安全的,这种多方过程是完全顺序的:先是一个人参与,然后是第二个,接着是第三个……所有的参与者甚至不需要提前知道;新参与者可以直接加到最后面。这使得可信设置容易有很多参与者,在实践中使其变得相当安全。
第二个改进是,它依赖的"华丽密码学"仅是一个标准化组件,称为“多项式承诺”。PLONK 使用基于可信设置和椭圆曲线配对的“Kate commitments”,但你也可以用其他方案替代,例如 FRI(这会 使 PLONK 成为一种 STARK)或基于隐藏阶群的 DARK。这意味着该方案在理论上可以兼容任何(可实现的)证明大小与安全假设之间的权衡。
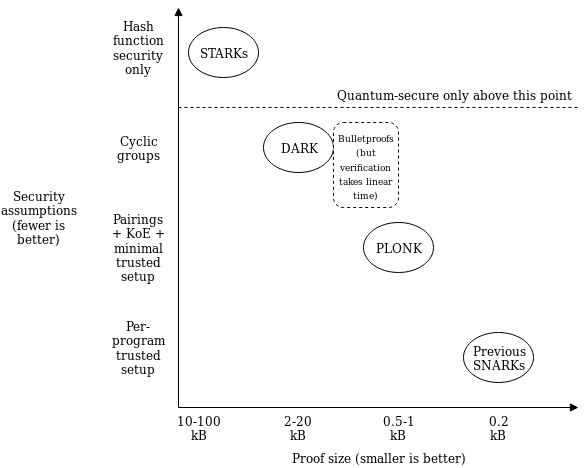
这意味着需要在证明大小与安全假设之间进行不同权衡的用例(或对这个问题有不同意识形态立场的开发者)仍然可以共享大部分相同的“算术化”工具——将程序转换为一组多项式方程,然后使用这些多项式承诺进行检查的过程。如果这种方案被广泛采用,我们可以期待快速进展以改善共享的算术化技术。
PLONK 的工作原理
让我们开始解释 PLONK 的工作原理,以一个有些抽象的格式,专注于多项式方程,而没有立即解释这些方程是如何被验证的。PLONK 的一个关键成分,如同 SNARKs 中使用的 QAPs,是将以下形式的问题转换为“给我一组满足一组数学方程的值”的过程:“给我一个值 X,使得我给你的特定程序 P 在 X 作为输入时,给出某个特定结果 Y”。程序 P 可以代表许多内容;例如,问题可以是“给我这个数独的解决方案”,你可以通过将 P 设置为数独验证器加上一些初始值进行编码,并设置 Y 为 1(即“是的,这个解决方案是正确的”),而一个满足条件的输入 X 将是数独的有效解决方案。这是通过将 P 表示为一个具有加法和乘法逻辑门的电路,并将其转换成一个方程系统,其中变量是所有电路线上的值,且每个门有一个方程(例如,x6=x4⋅x7 表示乘法,x8=x5+x9 表示加法)。
下面是寻找 x 的示例,使得 P(x)=x3+x+5=35(提示:x=3):
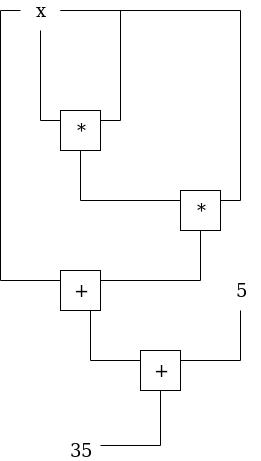
我们可以对门和线路进行如下标记:
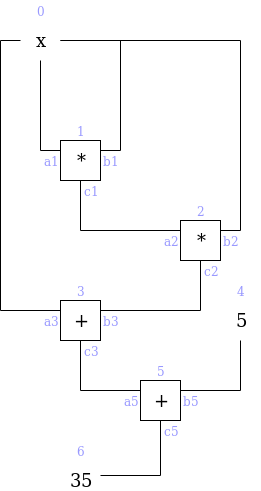
在门和线路上,我们有两种类型的约束:门约束(连接到同一门的线路之间的方程,例如 a1⋅b1=c1)和 复制约束(关于电路中不同线路的相等性的声明,例如 a0=a1=b1=b2=a3 或 c0=a1)。我们需要创建一个结构化的方程系统,最终减少为非常少量的多项式方程,以代表这两者。
在 PLONK 中,这些方程的设置如下。每个方程的形式为(思考:L = 左侧,R = 右侧,O = 输出,M = 乘法,C = 常数):
(QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+QCi=0
每个 Q 值是一个常数;每个方程中的常数(以及方程的数量)对于每个程序都是不同的。每个小写字母值是一个变量,由用户提供:ai 是第 i 个门的左输入线路,bi 是右输入线路,ci 是第 i 个门的输出线路。对于一个加法门,我们设置:
QLi=1,QRi=1,QMi=0,QOi=−1,QCi=0
将这些常数代入方程并简化,我们得到 ai+bi−ci=0,这正是我们想要的约束。对于乘法门,我们设置:
QLi=0,QRi=0,QMi=1,QOi=−1,QCi=0
对于设置 ai 为某个常数 x 的常数门,我们设置:
QL=1,QR=0,QM=0,QO=0,QC=−x
你可能注意到,每个线路的两端,以及一组明显必须具有相同值(例如 x)的线路,都是不同的变量;到目前为止,没有强制输出与其他门的输入相同(我们称之为“复制约束”)。PLONK 当然有办法强制复制约束,但我们稍后再讲。因此我们得到了一个问题,证明者想要证明他们有一堆 xai,xbi 和 xci 的值,让它们满足一堆相同形式的方程。这仍然是一个大问题,但与“寻找这个计算机程序的满足输入”不同的是这是一种非常 结构化 的大问题,我们有数学工具可以“压缩”它。
从线性系统到多项式
如果你阅读过 STARKs 或 QAPs,下面一节中描述的机制将希望感觉有些熟悉,但如果没有也没关系。这里的主要成分是理解一个 多项式 作为封装大量值为单个对象的数学工具。通常,我们以“系数形式”思考多项式,即如下表达式:
y=x3−5x2+7x−2
但我们也可以在“评估形式”中视多项式。例如,我们可以将上面的例子视为在坐标 (0,1,2,3) 处返回的评估值(−2,1,0,1)的 “度 < 4” 多项式。
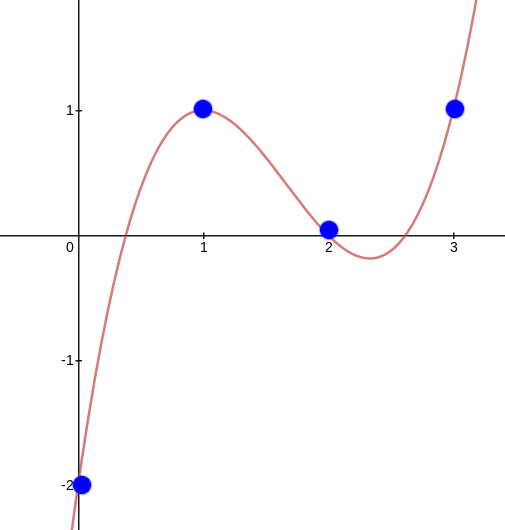
现在来看看下一步。许多同类方程系统可以重新解释为针对多项式的单个方程。例如,假设我们有系统:
2x1−x2+3x3=8x1+4x2−5x3=58x1−x2−x3=−2
我们定义四个多项式为评估形式:L(x) 是在坐标 (0,1,2) 处评估为 (2,1,8) 的度 < 3 的多项式,而在这些相同的坐标下,M(x) 评估为 (−1,4,−1),R(x) 评估为 (3,−5,−1),O(x) 评估为 (8,5,−2)(以这种方式直接定义多项式是可以的;你可以使用 拉格朗日插值 将其转换为系数形式)。现在,考虑方程:
L(x)⋅x1+M(x)⋅x2+R(x)⋅x3−O(x)=Z(x)H(x)
这里,Z(x) 是 (x−0)⋅(x−1)⋅(x−2) 的简写——在评估域 (0,1,2) 上返回零的最小(非平凡)多项式。此方程的解决方案 (x1=1,x2=6,x3=4,H(x)=0) 也满足原先的方程系统,不同之处在于原始系统不需要 H(x)。你还会注意到,在这种情况下,H(x) 方便地为零,但在更复杂的情况下,H 可能需要非零。
所以现在我们知道,可以用少数几个数学对象(多项式)来表示大量约束。但在上面我们构建的用于表示门线约束的方程中,x1,x2,x3 变量在每个方程中是不同的。我们可以通过让变量本身成为多项式而不是常数来处理这一点。于是我们得到:
QL(x)a(x)+QR(x)b(x)+QO(x)c(x)+QM(x)a(x)b(x)+QC(x)=0
和以前一样,每个 Q 多项式是一个可以从被验证程序生成的参数,而 a、b、c 多项式则是用户提供的输入。
复制约束
现在,让我们回到“连接”线路。目前为止,我们只有一堆关于不相交值的独立容易满足的方程:常数门可以通过将值设置为常数满足,加法和乘法门可以简单地通过将所有线路设置为零来满足!要使问题真正具有挑战性(并且实际上表示原始电路中编码的问题),我们需要添加一个验证“复制约束”的方程:例如 a(5)=c(7), c(10)=c(12) 等约束。这需要一些聪明的技巧。
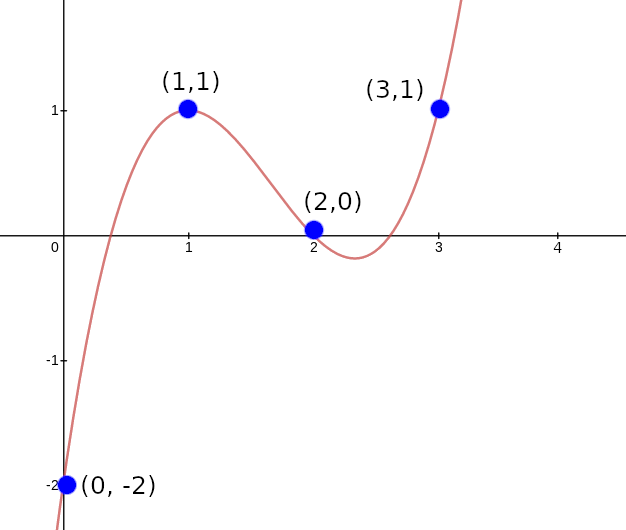
我们将采用的策略是设计一个“坐标对累加器”,一个多项式 p(x),其工作方式如下。首先,让 X(x) 和 Y(x) 是两个多项式,表示一组点的 x 和 y 坐标(例如,表示集合 ((0,−2),(1,1),(2,0),(3,1)) 你可能设置 X(x)=x 和 Y(x)=x3−5x2+7x−2)。我们的目标是让 p(x) 表示所有点直至(但不包括)给定位置,因此 p(0) 从 1 开始,p(1) 只表示第一个点,p(2) 表示第一个和第二个点,依此类推。我们将通过“随机”选择两个常数,v1 和 v2,并使用约束 p(0)=1 和 p(x+1)=p(x)⋅(v1+X(x)+v2⋅Y(x)) 构建 p(x),至少在域 (0,1,2,3) 内。
例如,将 v1=3 和 v2=2,我们得到:
| X(x) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Y(x) | -2 | 1 | 0 | 1 | |
| -1 | 6 | 5 | 8 | ||
| p(x) | 1 | -1 | -6 | -30 | -240 |
我们关注的结果是 p(4)=−240。现在,考虑一种情况,其中不是 X(x)=x,而是我们设定 X(x)=23x3−4x2+193x(即,该多项式在坐标 (0,1,2,3) 处评估为 (0,3,2,1))。如果你运行同样的过程,你会发现你也得到了 p(4)=−240。这不是巧合(实际上,如果你从足够大的域随机选择 v1 和 v2,这几乎永远不会偶然发生)。这发生的原因是 Y(1)=Y(3),因此如果你“交换点的 X 坐标”(1,1)和(3,1)你并没有改变点的集合,而因为累加器编码了一个集合(乘法不关心顺序),最终的值将是相同的。
现在我们可以开始看到用于证明复制约束的基本技巧。首先,考虑一个简单的案例,我们只想证明一个线路集内部的复制约束(例如,我们要证明 a(1)=a(3))。我们会制作两个坐标累加器:一个是 X(x)=x 和 Y(x)=a(x),另一个是 Y(x)=a(x),但 X′(x) 是评估为翻转(或以其他方式重排)每个复制约束中的值的置换多项式;在 a(1)=a(3) 这种情况下,这意味着该置换将以 03214 开始……第一个累加器将压缩 ((0,a(0)),(1,a(1)),(2,a(2)),(3,a(3)),(4,a(4))...,第二个 ((0,a(0)),(3,a(1)),(2,a(2)),(1,a(3)),(4,a(4))...。这两者能给出相同结果的唯一方式是 a(1)=a(3)。
为了证明 a、b 和 c 之间的约束,我们使用相同的程序,但相应地“累加”三个多项式中的点。我们为 a、b、c 分配一组 X 坐标(例如,a 得到 Xa(x)=x,即 0...n−1,b 得到 Xb(x)=n+x,即 n...2n−1,c 得到 Xc(x)=2n+x,即 2n...3n−1)。为了证明跨不同线路集之间的复制约束,"交替" X 坐标将是从三个集群中跨越一个置换的切片。例如,如果我们要证明 a(2)=b(4),且 n=5,则 Xa′(x) 的评估值将有 {0,1,9,3,4} 而 Xb′(x) 将有 {5,6,7,8,2}(请注意 2 和 9 发生了翻转,9 对应于 b4 线路)。通常,Xa′(x),Xb′(x) 和 Xc′(x) 也称为 σa(x),σb(x) 和 σc(x)。
然后,代替在程序的单次运行上检查相等性(即检查 p(4)=p′(4)),我们会检查 三个不同运行的乘积:
pa(n)⋅pb(n)⋅pc(n)=pa′(n)⋅pb′(n)⋅pc′(n)
三个 p(n) 的评估值乘积在每一侧累加 a、b 和 c 运行中的 所有 坐标对,因此这允许我们进行与之前相同的检查,不同之处在于现在我们可以不仅检查在一组线路 a、b 或 c 中的位置之间的复制约束,而且还可以在集群之间(例如,如在 a(2)=b(4) 中)。
这就是一切!
整合所有内容
实际上,所有这些数学运算是在素数域上完成的;请查看 这里 的“模数学插曲”部分,以了解素数域是什么。此外,出于数学原因,最好在阅读和理解 这篇关于 FFT 实现的文章 后再理解,我们在引用线索索引时,将不直接使用 x=0....n−1,而是使用 ω 的幂:1,ω,ω2....ωn−1,其中 ω 是域中的高阶单位根。这不会改变数学,只是坐标对累加器的约束检查方程会从 p(x+1)=p(x)⋅(v1+X(x)+v2⋅Y(x)) 变为 p(ω⋅x)=p(x)⋅(v1+X(x)+v2⋅Y(x)),而代替用 0..n−1, n..2n−1, 2n..3n−1 作为坐标,我们使用 ωi,g⋅ωi 和 g2⋅ωi,g 可以是域中的任意高阶元素。
现在让我们列出所有需要检查的方程。首先是主要的门约束满足检查:
QL(x)a(x)+QR(x)b(x)+QO(x)c(x)+QM(x)a(x)b(x)+QC(x)=0
然后是多项式累加器的迁移约束(注意:“=Z(x)⋅H(x)”意味着“在我们关心的特定域内均为零,但不必在域外也是如此”):
Pa(ωx)−Pa(x)(v1+x+v2a(x))=Z(x)H1(x) Pa′(ωx)−Pa′(x)(v1+σa(x)+v2a(x))=Z(x)H2(x) Pb(ωx)−Pb(x)(v1+gx+v2b(x))=Z(x)H3(x) Pb′(ωx)−Pb′(x)(v1+σb(x)+v2b(x))=Z(x)H4(x) Pc(ωx)−Pc(x)(v1+g2x+v2c(x))=Z(x)H5(x) Pc′(ωx)−Pc′(x)(v1+σc(x)+v2c(x))=Z(x)H6(x)
然后是多项式累加器的起始和结束约束:
Pa(1)=Pb(1)=Pc(1)=Pa′(1)=Pb′(1)=Pc′(1)=1 Pa(ωn)Pb(ωn)Pc(ωn)=Pa′(ωn)Pb′(ωn)Pc′(ωn)
用户提供的多项式包括:
- 线路分配 a(x)、b(x)、c(x)
- 坐标累加器 Pa(x)、Pb(x)、Pc(x)、Pa′(x)、Pb′(x)、Pc′(x)
- 商 H(x) 和 H1(x)...H6(x)
证明者和验证者需要提前计算的程序特定多项式为:
- QL(x)、QR(x)、QO(x)、QM(x)、QC(x),它们共同代表电路中的门(注意 QC(x) 编码公共输入,因此在运行时可能需要计算或修改)
- “置换多项式” σa(x)、σb(x) 和 σc(x),它们编码 a、b 和 c 线路之间的复制约束。
注意,验证者只需存储对这些多项式的承诺。上述方程中唯一剩余的多项式是 Z(x)=(x−1)⋅(x−ω)⋅...⋅(x−ωn−1),其设计旨在在所有这些点上评估为零。幸运的是,可以选择 ω,使得这个多项式很容易评估:通常选择使 ωn=1,此时 Z(x)=xn−1。
这里有一个细微的地方:Pa(ωi+1) 和 Pa(ωi) 之间的约束不能在 ω 的 整个 幂的圈上都成立;在 ωn−1 处几乎总是为假,因为下一坐标是 ωn=1,这将我们带回到“累加器”的 起始;要解决这个问题,我们可以修改约束以表示“约束要么为真,要么 x=ωn−1”,我们可以通过乘以 x−ωn−1 来满足这个要求,这样在该点时它的值为零。
v1 和 v2 的唯一约束是,用户在 v1 和 v2 被确认后,不能选择 a(x)、b(x) 或 c(x),因此我们可以通过从 a(x)、b(x) 和 c(x) 的承诺的哈希计算 v1 和 v2 来满足这一点。
现在我们已经将程序满足问题转化为满足一些多项式方程的简单问题,PLONK 中还有一些优化,可以让我们删除以上方程中许多多项式,我将不深入探讨以保持简洁。但多项式本身,无论是程序特定的参数还是用户输入,都是 巨大 的。因此下一个问题是,我们如何绕过这个问题以使证明简短?
多项式承诺
一个 多项式承诺 是一个简短的对象,它“表示”一个多项式,允许你验证该多项式的评估,而无需实际包含多项式中的所有数据。也就是说,如果有人给你一个承诺 c,表示 P(x),他们可以给你一个证明,以说服你在某个特定 z 的情况下 P(z) 的值是多少。还有一个进一步的数学结果表示,在一个足够大的域中,如果关于在某个随机 z 处评估的多项式的特定类型方程(选择在 z 确定之前)为真,那么这些方程在整个多项式上也为真。例如,如果 P(z)⋅Q(z)+R(z)=S(z)+5,那么我们知道 P(x)⋅Q(x)+R(x)=S(x)+5 在一般情况下是极有可能的。使用这样的多项式承诺,我们可以非常容易地检查上面所有多项式方程——进行承诺,将其作为输入生成 z,证明每个多项式在 z 上的评估,然后运行这些方程,使用这些评估值替代原始多项式。但是,这些承诺是如何工作的呢?
有两个部分:对多项式 P(x) 的承诺 P(x)→c,和某个 z 的值 P(z) 的揭示。为了进行承诺,有许多技术;一个例子是 FRI,另一个是我将在下面描述的 Kate commitments。为了证明开放,它可以发现有一个简单的通用“减法与除法”技巧:要证明 P(z)=a,你证明:
P(x)−ax−z
也是一个多项式(使用另一个多项式承诺)。这之所以有效,是因为如果商是一个多项式(即它不是分数),那么 x−z 是 P(x)−a 的一个因子,因此 (P(x)−a)(z)=0,所以 P(z)=a。尝试使用一些多项式,例如 P(x)=x3+2⋅x2+5 和 (z=6,a=293) 来验证;再试试 (z=6,a=292) 看看它是如何失败的(如果你懒得做,看看 WolframAlpha 这里 与 这里 的区别)。还要注意一个通用优化:为了同时证明多个多项式的多个开口,在对输出制作承诺后,对多项式的 随机线性组合 和输出执行减法与除法技巧。
那么,这些承诺本身是如何工作的呢?幸运的是,Kate commitments 比 FRI 简单得多。一个可信设置程序生成一组椭圆曲线点 G,G⋅s,G⋅s2 .... G⋅sn,以及 G2⋅s,其中 G 和 G2 是两个椭圆曲线群的生成元,s 是一个秘密,该秘密在过程完成后被遗忘(注意,这里有一个多方的设置版本,它是安全的,只要参与者有至少一人遗忘了他们的秘密份额)。这些点被公开并认为是该方案的“证明密钥”;任何需要进行多项式承诺的人都需要使用这些点。对一个度 d 的多项式进行承诺,通过将证明密钥中的每个前 d+1 个点乘以多项式中相应的系数,并将结果相加来完成。
注意,这为多项式在 s 处提供了一个“评估”,而无需知道 s。例如,x3+2x2+5 将表示为 (G⋅s3)+2⋅(G⋅s2)+5⋅G。我们可以使用表示 [P] 的符号来指代以这种方式编码的 P(即 G⋅P(s))。在执行减法与除法技巧时,你可以通过使用 椭圆曲线配对 来证明两个多项式实际上满足该关系:检查 e([P]−G⋅a,G2)=e([Q],[x]−G2⋅z)作为检查 P(x)−a=Q(x)⋅(x−z) 的代理。
但最近还有其他类型的多项式承诺出现。一个新方案称为 DARK(“知识的丢番图论证”)使用“隐藏阶群”,例如 类群 来实现另一种多项式承诺。隐藏阶群是独特的,因为它们允许你将任意大的数字压缩为群元素,甚至比群元素的大小还要大,以一种无法被“伪造”的方式;从 VDF 到 累加器 再到范围证明以及多项式承诺,都可以基于此构建。另一种选择是使用大气透明度(bulletproofs),使用常规椭圆曲线群,代价是证明需要更长时间来验证。由于多项式承诺比全面的零知识证明方案简单得多,因此我们可以期待未来会创造出更多这样的方案。
总结
最后,我们再回顾一下该方案。给定一个程序 P,你将其转换为一个电路,并生成一组方程,其形式如下:
(QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+QCi=0
然后你将这一组方程转换为一个单一的多项式方程:
QL(x)a(x)+QR(x)b(x)+QO(x)c(x)+QM(x)a(x)b(x)+QC(x)=0
你还从电路中生成一系列复制约束。从这些复制约束中,你生成三个表示置换线路索引的多项式:σa(x)、σb(x)、σc(x)。为了生成证明,你计算所有线路的值并将其转换为三个多项式:a(x)、b(x)、c(x)。你还计算六个作为置换检查参数的“坐标对累加器”多项式。最后,你计算共同因子 Hi(x)。
有一组方程需要在多项式之间进行检查;你可以通过为多项式进行承诺,在某个随机 z 上打开它们(及其开口是正确的证明),并用这些评估代替原始多项式来运行方程。证明本身只需几个承诺和开口,并且可以通过几个方程进行验证。就是这样!
- 原文链接: vitalik.eth.limo/general...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊执行层优化:状态树与虚拟机 91 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 102 浏览
- 首次 ZK 攻击发生,且出乎意料 125 浏览
- Vitalik: 以太坊量子抵抗路线图 90 浏览
- zkMesh:2026年2月回顾 114 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 88 浏览
- 量子可恢复的 Zcash 69 浏览
- ZK编年史:哈希登场 226 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 420 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 340 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 456 浏览
- Zcash:比特币遗忘的隐私 474 浏览

