ZK的算术电路

在零知识证明的背景下，算术电路是一个方程系统，它模拟了NP中的一个问题。

我们在文章P vs NP中提到的一个关键点是，P或NP中的任何问题的解决方案都可以通过将该问题建模为布尔电路来验证。

然后，我们将原始问题的解决方案转换为布尔变量的一组值（称为见证），这些值可以使布尔电路返回真值。

这篇文章建立在上述链接的文章基础上，因此请首先阅读那篇文章。

算术电路作为布尔电路的替代方案

使用布尔电路表示问题解决方案的一个缺点是，当表示算术运算（例如加法或乘法）时，可能会非常冗长。

例如，如果我们想表示 $a + b = c$，其中 $a = 8, b = 4, c = 12$，我们必须将 $a$，$b$ 和 $c$ 转换为二进制数。二进制数字中的每一位都将对应一个不同的布尔变量。在此示例中，假设我们需要 4 位来编码 $a$，$b$ 和 $c$，其中 $a₀$ 表示最不重要位(LSB)，$a₃$ 表示最重要位(MSB)，如下所示：

• a₃, a₂, a₁, a₀
  • $a = 1000$
• b₃, b₂, b₁, b₀
  • $b = 0100$
• c₃, c₂, c₁, c₀
  • $c = 1100$

（目前你无需了解如何将数字转换为二进制，我们将在后面的文章中解释此方法）。

一旦我们将 $a$，$b$ 和 $c$ 写成二进制形式，我们就可以编写一个布尔电路，其输入为所有二进制数字 $(a₀, a₁, …, c₂, c₃)$。我们的目标是编写这样的布尔电路，使电路仅当 $a + b = c$ 时输出真值。

事实证明，这比预期的要复杂，因为以下大电路模拟了二进制中的 $a + b = c$。为了简洁起见，我们不显示推导。我们只显示公式以说明这样的电路有多冗长：

((a₄ ∧ b₄ ∧ c₄) ∨ (¬a₄ ∧ ¬b₄ ∧ c₄) ∨ (¬a₄ ∧ b₄ ∧ ¬c₄) ∨ (a₄ ∧ ¬b₄ ∧ ¬c₄)) ∧

((a₃ ∧ b₃ ∧ ((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
 (¬a₃ ∧ ¬b₃ ∧ ((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
 (¬a₃ ∧ b₃ ∧ ¬((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
 (a₃ ∧ ¬b₃ ∧ ¬((a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))) ∧

((a₂ ∧ b₂ ∧ ((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))) ∨
 (¬a₂ ∧ ¬b₂ ∧ ((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))) ∨
 (¬a₂ ∧ b₂ ∧ ¬((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀)))) ∨
 (a₂ ∧ ¬b₂ ∧ ¬((a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))) ∧

((a₁ ∧ b₁ ∧ c₀) ∨ (¬a₁ ∧ ¬b₁ ∧ c₀) ∨ (¬a₁ ∧ b₁ ∧ ¬c₀) ∨ (a₁ ∧ ¬b₁ ∧ ¬c₀)) ∧

((a₀ ∧ b₀ ∧ c₀) ∨ (¬a₀ ∧ ¬b₀ ∧ c₀) ∨ (¬a₀ ∧ b₀ ∧ ¬c₀) ∨ (a₀ ∧ ¬b₀ ∧ ¬c₀)) ∧

¬ ((a₄ ∧ b₄) ∨
     (b₄ ∧ (a₃ ∧ b₃) ∨ (b₃ ∧ (a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))) ∨
     (a₃ ∧ (a₂ ∧ b₂) ∨ (b₂ ∧ (a₁ ∧ b₁) ∨ (b₁ ∧ c₀) ∨ (a₁ ∧ c₀))))

关键在于，如果我们仅限于布尔输入和基本的布尔运算（与、或、非），构建电路可能会迅速变得复杂且繁琐，对于涉及算术运算的基本问题尤为如此。

相比之下，直接在电路中表示数字将更简单。我们不再用布尔公式来建模加法，而是直接对这些数字进行加法和乘法运算。

本文证明也可以用 算术电路 来建模P或NP中的任何问题。

算术电路

算术电路是一个仅使用加法、乘法和相等的方程系统。与布尔电路一样，它检查所提出的输入集合是否有效，但不计算解决方案。

以下是第一个算术电路的示例：

6 = x₁ + x₂
9 = x₁x₂

我们说布尔电路是 满足 的，如果我们对输入变量有一个赋值，使输出为真。类似地，算术电路是满足的，如果可以对变量赋值，使所有的方程均成立。

例如，上述电路由 $x₁ = 3, x₂ = 3$ 满足，因为电路中的两个方程都成立。相反，电路由 x₁ = 1, x₂ = 6 不满足，因为方程 9 = x₁x₂ 不为真。

因此，我们可以将算术电路与电路中的方程集合互换思考。仅当这些输入使 所有 方程成立时，输入集才“满足电路”。

记号与术语

算术电路中的变量被称为 信号，因为我们将使用的编程语言 Circom 是这样称呼它们的。

要表示相等，我们将使用 === 运算符。我们使用这种记法是因为 Circom 使用它来表述两个信号持有相同的值，因此我们也应习惯看到它。

我们强调 === 表示左侧和右侧相等。例如，在以下电路中：

c === a + b

我们并不是将 a 加到 b 然后赋值给 c。而是我们假定值 a，b 和 c 作为输入提供，我们在断言它们之间的某种关系成立。这产生了对 a 和 b 的和进行 约束 的效果，使其等于 c。

把 c === a + b 视为完全等同于 assertEq(c, a + b)。同样，表达式 a + b === c * d 完全等同于 assertEq(a + b, c * d)。实质上，验证电路中的这些方程涉及检查某些条件（约束）是否被满足。证明其见证有效的代理可以为信号分配任何值。然而，只有在满足所有约束的情况下，他们的证明（见证）才会被视为有效。

例如，如果代理希望证明：

a === b + c + 3
a * u === x * y

他们必须从 电路外部 提供 (a, b, c, u, x, y) 并将其赋值给电路中的信号。

请记住，上述代码等同于：

assertEq(a, b + c + 3)
assertEq(a * u, x * y)

算术电路的一个有用心理模型是所有信号都被视为没有输出的输入。

为了强调这一点，我们在以下视频中提供了一个可视化。所有的信号都是输入，而使用 === 来检查而不是赋值。

视频中的电路可以写成：

z + y === x
x + y === u

而没有意义的变化。

算术电路 x === x + 1 并不是指 增加 x。这是一个没有解的算术电路，因为 x 不能等于 x + 1。因此不可能满足该约束。

解读算术电路

考虑以下电路：

x₁(x₁ - 1) === 0
x₁x₂ === x₁

第一个约束 x₁(x₁ - 1) === 0 限制了 x₁ 的可能值为 0 或 1。x₁ 的任何其他值都不会满足此约束。

在第二个约束 x₁x₂ === x₁ 中，我们有两种可能的情况：

• 如果 x₁ = 1，那么 x₂ 也必须为 1，否则第二个约束将无法满足。如果 x₁ = 1 且 x₂ ≠ 1，那么第二个方程成为 1 * x₂ === 1，只有 x₂ = 1 时才能满足，这将导致冲突。
• 如果 x₁ = 0 ，那么 x₂ 可以为任何值，因为 0x₂ === 0 很容易满足。

以下对 (x₁, x₂) 的赋值都是有效的见证：

• $(x₁, x₂) = (1, 1)$
• $(x₁, x₂) = (0, 2)$
• $(x₁, x₂) = (0, 1337)$
• $(x₁, x₂) = (0, 404)$

请记住，一个方程系统可以有许多解。同样，算术电路也可以有许多解。但是通常，我们只关心验证给定的解。我们无需为算术电路找到所有解。

布尔电路与算术电路的比较

下表显示布尔电路和算术电路之间的区别，但请牢记，它们服务于相同的目的：验证见证。

布尔电路	算术电路
变量为0, 1	信号为数字
唯一的运算是AND, OR, NOT	唯一的运算是加法和乘法
当输出为真时满足	当所有方程的左侧等于右侧时满足（没有输出）
见证是使布尔电路满足的布尔变量的赋值	见证是使所有相等约束满足的信号赋值

除了在某些情况下使用更少变量的便利，算术电路和布尔电路都是完成相同工作的工具——证明你有一个NP问题的见证。

回归初始示例 a + b = c

让我们重新审视上述示例：编写一个 布尔 电路来表示方程 a + b = c，其中我们给定 c = 12。对于布尔电路，我们需要将 a，b 和 c 编码为二进制，每个需要4位（在此示例中）。总体而言，我们有12个输入到电路。相比之下，算术电路只需3个输入：a，b 和 c。输入数量和整体电路规模的减少是我们更倾向于在ZK应用中使用算术电路的原因。

方程组与算术电路之间的相似性

布尔电路始终具有一个表达式，如果见证满足，返回真或假。

例如，如果我们有一组信号 $x$，$y$ 和 $z$，且我们希望约束 $x$ 和 $y$ 的和为5，那么我们需要一个单独的方程来满足该约束。我们希望约束 $z$ 的任何方式均有自己的单独方程。

为了证明算术电路和布尔电路是等效的，我们将在后面展示，任何布尔电路都可以转换为算术电路。这显示了它们可以交替使用，以证明一个代理对P或NP问题有见证。

所有的P问题都是NP问题的一个子集

正如在前一章中讨论的P vs NP，所有的P问题都是NP问题的子集，在验证见证的计算要求方面，因此我们将只提及NP问题，理解这包括P。

我们的结论是，如果NP中的任何问题的解决方案可以用布尔电路建模，那么NP（或P）中的任何问题的解决方案都可以用算术电路建模。

但在展示它们的等价性之前，我们将提供建模NP中问题解决方案的示例，以便我们理解算术电路是如何使用的。

算术电路示例

在第一个示例中，我们重新处理了澳大利亚的3着色问题。在第二个示例中，我们演示如何使用算术电路证明一个列表是有序的。

示例 1：使用算术电路建模3着色

当我们使用布尔电路建模3着色时，每个领土都有3个布尔变量——每种颜色一个——指示该国家是否被分配了该颜色。然后我们添加约束，以强制每个领土具有恰好一种颜色（颜色约束）以及强制相邻领土不得具有相同颜色（边界约束）。

使用算术电路建模此问题更容易，因为我们可以为每个领土分配一个信号，其可能值为 $\set{1, 2, 3}$ 来模拟它们的颜色，而不是三个布尔变量。我们可以任意将颜色分配给这些数字，例如 blue = 1，red = 2，和 green = 3。

对于每个领土，我们将单个颜色约束写成：

0 === (1 - x) * (2 - x) * (3 - x)

以强制每个领土具有恰好一种颜色。只有当 x 为 1、2 或 3 时，上述约束才能满足。

澳大利亚的3着色

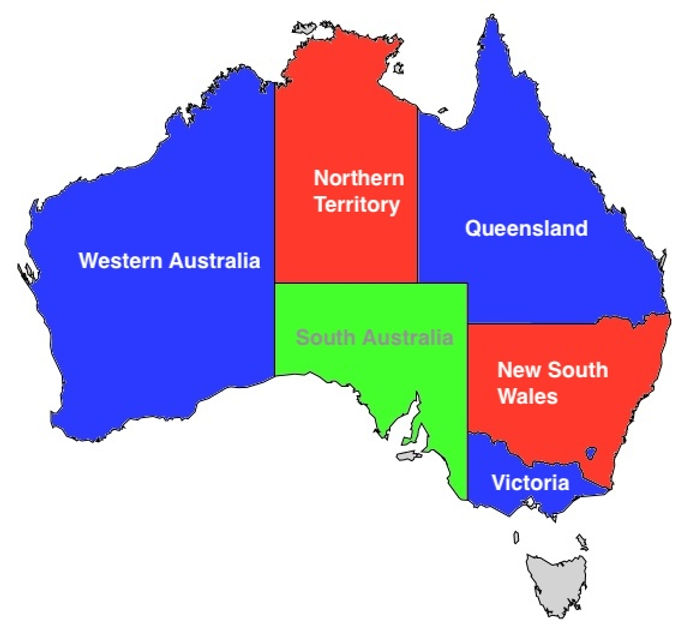
请记住，澳大利亚有六个领土：

• WA = 西澳大利亚
• SA = 南澳大利亚
• NT = 北领地
• Q = 昆士兰
• NSW = 新南威尔士
• V = 维多利亚

说 WA = 1 等同于说“将西澳大利亚涂成蓝色”。同样，WA = 2 意味着“红色”被分配给西澳大利亚，而 WA = 3 意味着“绿色”被分配。

我们对每个领土的颜色约束（使每个领土为蓝色，红色或绿色）变为：

1) 0 === (1 - WA) * (2 - WA) * (3 - WA)
2) 0 === (1 - SA) * (2 - SA) * (3 - SA)
3) 0 === (1 - NT) * (2 - NT) * (3 - NT)
4) 0 === (1 - Q) * (2 - Q) * (3 - Q)
5) 0 === (1 - NSW) * (2 - NSW) * (3 - NSW)
6) 0 === (1 - V) * (2 - V) * (3 - V)

我们现在想要确认邻近领土没有相同颜色的约束。实现这一点的一种方法是将邻近领土的信号相乘，并确保结果是“可接受”的。考虑相邻领土 x 和 y 的下表：

x	y	积
1	1	1
1	2	2
1	3	3
2	1	2
2	2	4
2	3	6
3	1	3
3	2	6
3	3	9

如果两个信号（相邻领土）相同，那么它们的乘积将为 $\set{1,4,9}$ 之一，即上表中的红色数字。如果 x 和 y 被约束为 1、2 或 3，并且互不相等，则它们的乘积 xy 将为 $\set{2, 3, 6}$ 之一。因此，如果 xy = 2 或 xy = 3 或 xy = 6，我们接受这个分配，因为这意味着两个邻近的领土有不同的颜色。

对于每对邻近领土 x 和 y，我们可以使用以下约束来强制它们不相等：

0 === (2 - xy) * (3 - xy) * (6 - xy)

上述方程在乘积 xy 等于 2、3 或 6 时成立。

边界约束由遍历边界并在每对邻近领土之间应用边界约束来创建，如以下视频所示：

我们现在展示边界约束：

西澳大利亚和南澳大利亚：
7) 0 === (2 - WA * SA) * (3 - WA * SA) * (6 - WA * SA)

西澳大利亚和北领地
8) 0 === (2 - WA * NT) * (3 - WA * NT) * (6 - WA * NT)

北领地和南澳大利亚
9) 0 === (2 - NT * SA) * (3 - NT * SA) * (6 - NT * SA)

北领地和昆士兰
10) 0 === (2 - NT * Q) * (3 - NT * Q) * (6 - NT * Q)

南澳大利亚和昆士兰
11) 0 === (2 - SA * Q) * (3 - SA * Q) * (6 - SA * Q)

南澳大利亚和新南威尔士
12) 0 === (2 - SA * NSW) * (3 - SA * NSW) * (6 - SA * NSW)

南澳大利亚和维多利亚
13) 0 === (2 - SA * V) * (3 - SA * V) * (6 - SA * V)

昆士兰和新南威尔士
14) 0 === (2 - Q * NSW) * (3 - Q * NSW) * (6 - Q * NSW)

新南威尔士和维多利亚
15) 0 === (2 - NSW * V) * (3 - NSW * V) * (6 - NSW * V)

通过将两者结合，我们看到，我们有一个完整的算术电路，用于证明我们拥有有效的澳大利亚3着色：

// 颜色约束
0 === (1 - WA) * (2 - WA) * (3 - WA)
0 === (1 - SA) * (2 - SA) * (3 - SA)
0 === (1 - NT) * (2 - NT) * (3 - NT)
0 === (1 - Q) * (2 - Q) * (3 - Q)
0 === (1 - NSW) * (2 - NSW) * (3 - NSW)
0 === (1 - V) * (2 - V) * (3 - V)

// 边界约束
0 === (2 - WA * SA) * (3 - WA * SA) * (6 - WA * SA)
0 === (2 - WA * NT) * (3 - WA * NT) * (6 - WA * NT)
0 === (2 - NT * SA) * (3 - NT * SA) * (6 - NT * SA)
0 === (2 - NT * Q) * (3 - NT * Q) * (6 - NT * Q)
0 === (2 - SA * Q) * (3 - SA * Q) * (6 - SA * Q)
0 === (2 - SA * NSW) * (3 - SA * NSW) * (6 - SA * NSW)
0 === (2 - SA * V) * (3 - SA * V) * (6 - SA * V)
0 === (2 - Q * NSW) * (3 - Q * NSW) * (6 - Q * NSW)
0 === (2 - NSW * V) * (3 - NSW * V) * (6 - NSW * V)

我们有15个约束，而变量（信号）的数量只减少了1/3。与每个领土的3个布尔变量相比，我们为每个领土只使用一个信号。在更大的电路中，这种复杂性和空间上的减少可能是相当显著的。

示例 2：证明列表已排序

给定数字列表 [a₁, a₂, ..., aₙ]，我们说该列表“已排序”，如果 aₙ ≥ aₙ₋₁ ≥ … a₃ ≥ a₂ ≥ a₁。换句话说，从后往前，这些数字是非递减的。

我们的目标是编写一个算术电路，验证列表是已排序的。

为此，我们需要一个算术电路来表达“$a ≥ b$”比较两个信号的关系。这看起来比想象的要复杂，因为算术电路只允许相等、加法和乘法，而不比较。

但假设我们有一个这样的“大于等于”电路——称为 GTE(a,b)。然后我们将构造比较每一对连续列表元素的电路：GTE(aₙ, aₙ₋₁), ..., GTE(a₃, a₂), GTE(a₂, a₁)，如果所有这些都满足，那么列表就是已排序的。

为了在没有 $≥$ 运算符的情况下比较两个十进制数字，我们首先需要一个算术电路来验证所提议的数字的二进制表示，所以我们首先稍微偏离一下，讨论二进制数字。

前提：二进制编码

我们用下标2表示二进制数字。例如，11₂是3，101₂是5。每个1和0被称为一位。我们说最左边的位是最重要位(MSB)，而最右边的位是最不重要位(LSB)。

正如我们稍后将显示的，当转换为十进制时，最重要的位乘以最大系数，而最不重要的位乘以最小系数。因此，如果我们将一个四位二进制数字写成 b₃b₂b₁b₀，b₃ 是 MSB，而 b₀ 是 LSB。

以下视频展示了1101₂转换为13：

如视频所示，四位二进制数可以使用以下公式转换为十进制数 v：

v = 8b₃ + 4b₂ + 2b₁ + b₀

这也可以写成：

v = 2³b₃ + 2²b₂ + 2¹b₁ + 2⁰b₀

例如，1001₂ = 9, 1010₂ = 10，依此类推。对于通用的 n 位二进制数字，转换为：

v = 2ⁿ⁻¹b₃ + ... + 2¹b₁ + 2⁰b₀

我们省略了如何将十进制数字转换为二进制的讨论。目前，如果读者希望转换为二进制，可以使用Python的内置 bin 函数：

>>> bin(3)
'0b11'
>>> bin(9)
'0b1001'
>>> bin(10)
'0b1010'
>>> bin(1337)
'0b10100111001'
>>> bin(404)
'0b110010100'

我们可以创建一个算术电路，声明“v 是一个四位二进制表示的十进制数字 b₃, b₂, b₁, b₀”的方法如下：

8b₃ + 4b₂ + 2b₁ + b₀ === v

// 强制“位”要么是0要么是1
b₀(b₀ - 1) === 0
b₁(b₁ - 1) === 0
b₂(b₂ - 1) === 0
b₃(b₃ - 1) === 0

信号 b₃, b₂, b₁, b₀ 被约束为 v 的二进制表示。如果 b₃, b₂, b₁, b₀ 不是二进制，或者不是 v 的二进制表示，则电路无法满足。

注意，对于信号 (v, b₃, b₂, b₁, b₀)，不存在满足条件的赋值使得 v > 15。也就是说，如果我们将 b₃, b₂, b₁, b₀ 全部设置为1，约束所允许的最高值，那么和将只能等于15。更高的和是无法添加的。在ZK中，这有时被称为对 v 的 范围检查。上述电路不仅展示了 v 的二进制表示，还强制 v < 16。

我们可以将其概括为以下电路，该电路对 $v < 2^n$ 施加限制，同时也提供 v 的二进制表示：

2ⁿ⁻¹bₙ₋₁ +...+ 2²b₂ + 2¹b₁ + b₀ === v
b₀(b₀ - 1) === 0
b₁(b₁ - 1) === 0
//...
bₙ₋₁(bₙ₋₁ - 1) === 0

说一个数字v以最多 n 位编码等同于说 $v < 2^n$。

为了感知 $2^n$ 作为 $n$ 的函数如何变化，考虑以下表格：

n 位	最大值（二进制）	最大值（十进制）	2ⁿ（十进制）	2ⁿ（二进制）
2	11₂	3	4	100
3	111₂	7	8	1000
4	1111₂	15	16	10000
5	11111₂	31	32	100000

请注意，二进制中的数字 $2^n$ 需要比数字 $2^n - 1$ 多1位来存储。通过将要素的编码位数限制到 $n$ 位，它强制该数字小于 $2^n$。

记住2的幂和所需的存储位数之间的关系是有帮助的。

• $2^n$ 需要存储 $n + 1$ 位。例如，$2^0=1_2$，$2^1 = 10_2$，$2^2=100_2$，$2^3=1000_2$ 等等。
• $2^{n-1}$ 是 $2^n$ 的一半，并且需要存储 $n$ 位
• $2^n − 1$ 需要存储 $n$ 位。当所有位都设置为1时，它是我们可以用 $n$ 位存储的最大值。

如果我们取一个数字 $n$ 并计算 $2^n$，我们就得到一个 $n + 1$ 位的数字，其最重要的位为1，其他均为零。 当 $n = 3$ 时，以下示例如下：

$$ 2^n=\underbrace{1000}_{n+1\space bits} $$

$2^{n-1}$ 相当于 $2^n / 2$。因为它被写成2的某种幂，因此它仍具有1的最重要的位和零的其余部分，但它需要的存储位数将少一位。

$$ 2^{n-1}=\underbrace{100}_{n\space bits} $$

$2^n −1$ 是一个 $n$ 位数字，其所有位均设置为1。

$$ 2^n-1=\underbrace{111}_{n\space bits} $$

在二进制中计算 ≥

如果我们在计算固定大小的二进制数字$ n $ 位时，$ 2^{n-1} $ 是特殊的，因为我们可以很容易地断言一个 $ n $ 位二进制数字大于或等于 $ 2^{n-1} $——或者小于它。我们称 $ 2^{n-1} $ 为“中点”。以下视频说明了如何比较 $ n $ 位数字与 $ 2^{n-1} $ 的大小：

通过检查 $ n $ 位数字的最重要位，我们可以判断该数字是否大于或等于 $ 2^{n-1} $ 或小于 $ 2^{n-1} $。

如果我们计算 $ 2^{n-1} + \Delta $ ，并查看该和的最重要位，我们可以快速判断 $\Delta $ 是正数还是负数。如果 $\Delta $ 是负的，则 $ 2^{n-1} + \Delta $ 必须小于 $ 2^{n-1} $。

检测 $ u \ge v $

如果我们用 $ u – v $ 来替换 $ \Delta $ ，那么 $ 2^{n-1} + (u – v) $ 的最重要位告诉我们 $ u ≥ v $ 还是 $ u < v $。

防止 $ 2^{n-1} + (u – v) $ 溢出

如果我们限制 $ u $ 和 $ v $ 表示为最多 $ n – 1 $ 位，而 $ 2^{n-1} $ 用 $ n $ 位表示，则下溢和溢出都不会发生。当 $ u $ 和 $ v $ 都用最多 $ n – 1 $ 位表示时，$ |u – v| $ 的最大绝对值是一个 $ n – 1 $ 位数字。

我们看到，在这种情况下 $ 2^{n-1} + (u – v) $ 不会出现下溢，因为 $ 2^{n-1} $ 至少比 $ |u – v| $ 大1位。

现在考虑溢出情况。为了不失一般性，对于 $ n = 4 $，即四位数字，$ 2^{n-1} = 2^{4-1} = 8 $ 或 $ 1000_2 $。作为3位数字，$ |u – v| $ 能容纳的最大值是 $ 111_2 $。将 $ 1000_2 + 111_2 $ 相加的结果为 $ 1111_2 $，并不是溢出。

对于 $ u ≥ v $ 的算术电路的总结

• 我们约束 $ u $ 和 $ v $ 为最多 $ n – 1 $ 位数字。
• 我们创建一个算术电路，编码 $ 2^{n-1} + (u – v) $ 的二进制表示，使用 $ n $ 位。
• 如果 $ 2^{n-1} + (u – v) $ 的最重要位是1，那么 $ u ≥ v $ ，反之亦然。

最终的算术电路如下，用于检查如果 $ u \geq v $ 的条件，同时 $ u $ 和 $ v $ 是 $ n – 1 $ 位数字。我们固定 $ n = 4 $，这意味着 $ u $ 和 $ v $ 必须被约束为3位数字。感兴趣的读者可以将其推广为其他值的 $ n $：

// u 和 v 的表示最多为3位：
2²a₂ + 2¹a₁ + a₀ === u
2²b₂ + 2¹b₁ + b₀ === v

// 对 aᵢ, bᵢ 进行 0 1 限制
a₀(a₀ - 1) === 0
a₁(a₁ - 1) === 0
a₂(a₂ - 1) === 0
b₀(b₀ - 1) === 0
b₁(b₁ - 1) === 0
b₂(b₂ - 1) === 0

// 二进制表示 2ⁿ⁻¹ + (u - v)
2³ + (u - v) === 8c₃ + 4c₂ + 2c₁ + c₀

// 对 cᵢ 进行 0 1 限制
c₀(c₀ - 1) === 0
c₁(c₁ - 1) === 0
c₂(c₂ − 1) === 0
c₃(c₃ − 1) === 0

// 检查 MSB 是否为 1
c₃ === 1

断言列表已排序

现在我们有了比较信号的算术电路，我们将重复此电路针对列表中的每对顺序元素并验证它已排序。

示例总结

我们展示了如何创建一个算术电路来建模前一章节中的解决方案。

我们现在可以概括说，我们可以使用算术电路建模NP中的任何问题。

如何使用算术电路建模布尔电路

任何布尔电路都可以用算术电路建模。这意味着我们可以定义一个将布尔电路B转换为算术电路A的过程，使得满足B的输入集合可以转换为满足A的信号集合。以下，我们概述此过程的关键组成部分，并演示将特定布尔电路转换为算术电路的示例。

假设我们有以下布尔公式： out = (x ∧ ¬ y) ∨ z。如果（x 为真且 y 为假） 或 z 为真，则该公式为真。

我们将 x，y 和 z 编码为算术电路信号，并限制它们的值为0或1。

以下算术电路仅在 x，y 和 z 都为0或1时才能满足。

x(x - 1) === 0
y(y - 1) === 0
z(z - 1) === 0
```现在让我们展示如何将布尔电路运算符映射到算术电路运算符，假设输入变量被限制为 0 或 1。

### 与门

我们将布尔与 `t = u ∧ v` 转换为算术电路如下：

```javascript
u(u - 1) === 0
v(v - 1) === 0
t === uv

当且仅当 u 和 v 都为 1 时，t 才会是 1，因此该算术电路模拟了一个与门。由于约束 u(u - 1) = 0 和 v(v - 1) = 0，t 只能是 0 或 1。

非门

我们将布尔非 t = ¬u 转换为算术电路如下：

u(u - 1) === 0
t === 1 - u

当 u 为 0 时，t 为 1，反之亦然。由于约束 u(u - 1) === 0，t 只能是 0 或 1。

或门

我们将布尔或 t === u ∨ v 转换为算术电路如下：

u(u - 1) === 0
v(v - 1) === 0
t === u + v - uv

为了说明它为什么模拟或门，可以考虑以下表格：

u	v	u + v	uv	t (u + v – uv)
0	0	0	0	0
0	1	1	0	1
1	0	1	0	1
1	1	2	1	1

如果 u 或 v 为 1，则 t 至少为 1。为了防止 t 等于 2（这在布尔运算符中是无效输出），我们减去 uv，当 u 和 v 都为 1 时，uv 将为 1。

请注意，对于上述所有门，我们无需施加约束 t(t - 1) === 0。输出 t 隐式约束为 0 或 1，因为没有输入赋值会导致 t 的值为 2 或更大。

将 out = (x ∧ ¬ y) ∨ z 转换为算术电路

现在我们已经看到如何将所有允许的布尔电路运算转换为算术电路，让我们来看一个将布尔电路转换为算术电路的例子。

创建 0 1 约束

x(x - 1) === 0
y(y - 1) === 0
z(z - 1) === 0

用算术电路替换 ¬ y

out = (x ∧ ¬ y) ∨ z

out = (x ∧ (1 – y)) ∨ z

用算术电路替换 ∧

out = (x ∧ (1 – y)) ∨ z

out = (x(1 – y)) ∨ z

用算术电路替换 ∨

out = (x(1 – y)) ∨ z

out = (x(1 – y)) + z – (x(1 – y))z

我们最终的算术电路为 out = (x ∧ ¬ y) ∨ z 如下：

x(x - 1) === 0
y(y - 1) === 0
z(z - 1) === 0
out === (x(1 - y)) + z - (x(1 - y))z

如果需要，我们可以简化最后的方程：

out === (x(1 - y)) + z - ((x(1 - y))z)
out === x - xy + z - ((x - xy)z)
out === x - xy + z - (xz - xyz)

out === x - xy + z - xz + xyz

我们也可以以无意义的改变如下方式编写算术电路：

x² === x
y² === y
z² === z
out === x - xy + z - xz + xyz

总结

如果 NP 中每个问题的解决方案可以用布尔电路表示，而每个布尔电路可以转换为等效的算术电路，那么可以得出结论，NP 中每个问题的解决方案也可以用算术电路来表示。

在实践中，ZK 开发者更倾向于使用算术电路而非布尔电路，因为如上所示，它们通常需要更少的变量来完成相同的任务。

不需要先计算布尔电路再将其转换为算术电路。我们可以直接用算术电路模型化 NP 问题的解决方案。

下一步

我们在本文中略过了两个非常重要的细节。存在一些其他需要解决的挑战。例如：

• 我们没有讨论用于存储算术电路信号的数据类型，以及如何处理加法或乘法中的溢出。
• 我们没有办法在不损失精度的情况下表达值 2/3。我们选择的任何固定点或浮点表示都会存在舍入问题。

为了解决这些问题，算术电路是对 有限域 进行计算: 数学的一个分支，其中所有加法和乘法都是模一个质数进行的。

有限域算术与常规算术具有一些由模运算引入的惊人差异，因此下一章将详细探讨它们。

通过 RareSkills 了解更多

在我们的免费的 ZK 书中了解更多关于 零知识证明 的内容。本教程是该书中的一章。

练习题

1. 创建一个算术电路，该电路接收信号 x₁、x₂、……、xₙ，并在_至少_一个信号为 0 时被满足。

2. 创建一个算术电路，该电路接收信号 x₁、x₂、……、xₙ，并在所有信号为 1 时被满足。

3. 二分图是可以用两种颜色进行着色的图，使得没有两个相邻的节点共享相同的颜色。设计一个算术电路方案，表明你有一个有效的二色着色图的证据。提示：本教程中的方案需要调整才能适用于二色着色。

4. 创建一个算术电路，将 k 限制为 x、y 或 z 中的最大值。即如果 x 是最大值，k 应等于 x，y 和 z 亦然。

5. 创建一个算术电路，接收信号 x₁、x₂、……、xₙ，限制它们为二进制，并在 _至少_一个信号为 1 时输出 1。提示：这个比看上去更棘手。考虑将你在前两个问题中学到的知识结合并使用 NOT 门。

6. 创建一个算术电路，以确定信号 v 是否是 2 的幂（1, 2, 4, 8，等）。提示：创建一个算术电路，将另一组信号限制为编码 v 的二进制表示，然后对这些信号添加额外的限制。

7. 创建一个算术电路来建模 子集和问题。给定一组整数（假设它们都是非负的），确定是否存在一个子集使其和等于给定值 $k$。例如，给定集合 $\set{3,5,17,21}$ 和 $k = 22$，存在一个子集 $\set{5, 17}$ 使其和为 $22$。当然，子集和问题不一定有解。

提示
使用一个 0 或 1 的“开关”，表示一个数字是否为子集的一部分。

8. 覆盖集合问题从集合 $S = \set{1, 2, …, 10}$ 开始，并且有几个明确的 $S$ 的子集，例如：$\set{1, 2, 3}$、$\set{3, 5, 7, 9}$、$\set{8, 10}$、$\set{5, 6, 7, 8}$、$\set{2, 4, 6, 8}$，并询问我们是否可以至多选择 $k$ 个 $S$ 的子集，使它们的并集为 $S$。在上面的例子问题中，$k = 4$ 的答案为真，因为我们可以使用 $\set{1, 2, 3}$、$\set{3, 5, 7, 9}$、$\set{8, 10}$、$\set{2, 4, 6, 8}$。注意，对于每个问题，我们可以使用的子集都是在开始时确定的。我们无法自己构建子集。如果给我们子集 $\set{1,2,3}$、$\set{4,5}$、$\set{7,8,9,10}$，则没有解决方案，因为数字 $6$ 不在子集中。

另一方面，如果给定 $S = \set{1,2,3,4,5}$ 和子集 $\set{1}, \set{1,2}, \set{3, 4}, \set{1, 4, 5}$，并询问是否可以用 $k = 2$ 的子集覆盖，那么将没有解决方案。然而，如果 $k = 3$，则有效解决方案为 $\set{1, 2}, \set{3, 4}, \set{1, 4, 5}$。

我们的目标是证明对于给定集合 $S$ 和一组定义好的 $S$ 的子集列表，我们是否可以选择一组子集，使它们的并集为 $S$。具体来说，问题是我们是否可以用 $k$ 或更少的子集实现这一点。我们希望通过将问题编码为一个算术电路来证明我们知道使用哪些 $k$（或更少）个子集。

最初发布于 2024 年 4 月 23 日

• 原文链接： rareskills.io/post/arith...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～