Schwartz-Zippel 引理及其在零知识证明中的应用

几乎所有 ZK-Proof 算法都依赖于 Schwartz-Zippel 引理来实现简洁性。

Schwartz-Zippel 引理指出，如果我们有两个多项式 $p(x)$ 和 $q(x)$，它们的次数分别为 $d_p$ 和 $d_q$，并且 $p(x) \neq q(x)$，那么 $p(x)$ 和 $q(x)$ 的交点数量小于或等于 $\mathsf{max}(d_p, d_q)$。

让我们来看几个例子。

多项式示例与 Schwartz-Zippel 引理

一条直线与抛物线的交点

考虑多项式 $p(x) = x$ 和 $q(x) = x^2$。它们在 $x = 0$ 和 $x = 1$ 处相交。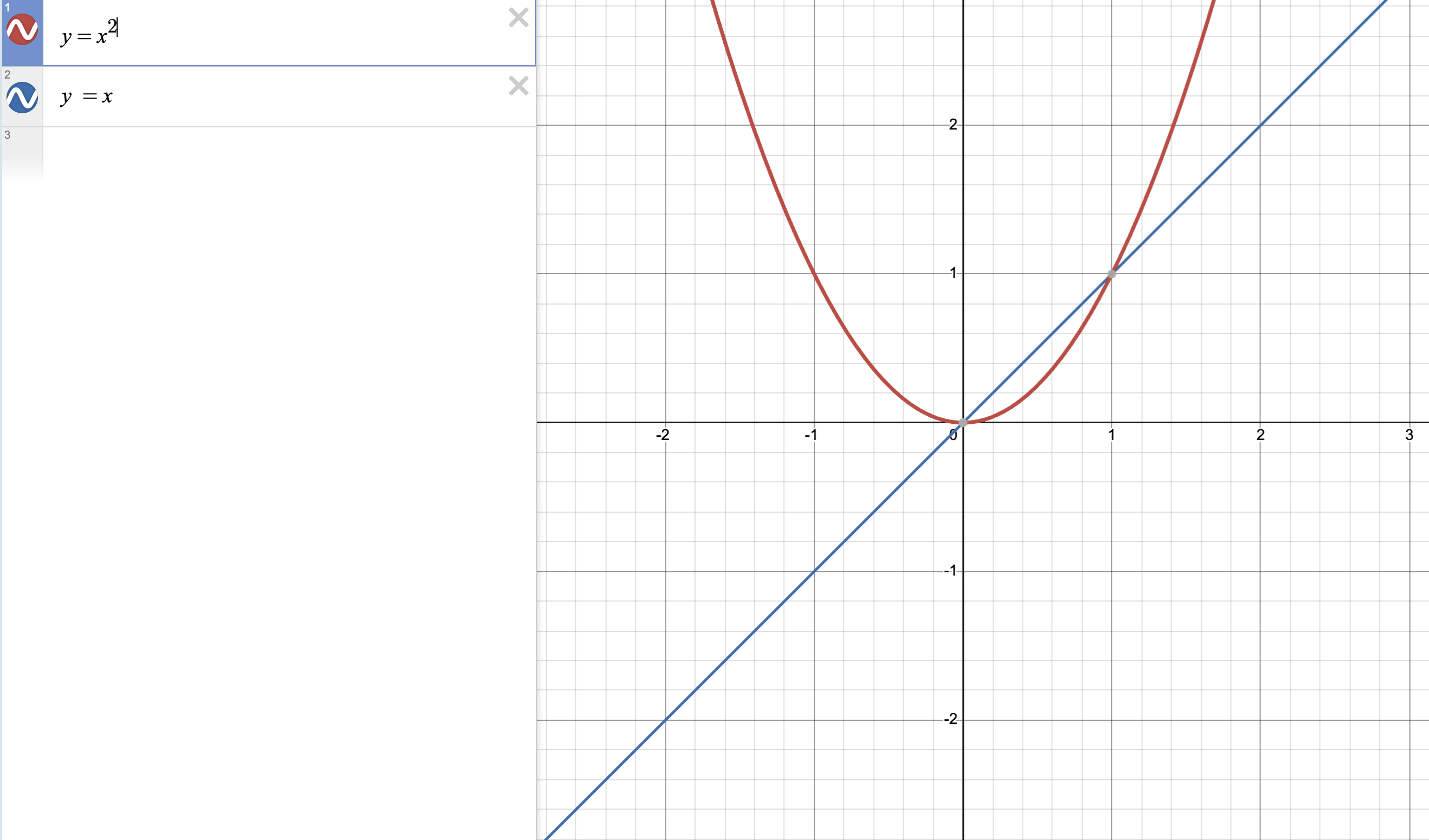

它们在两点相交，这是多项式 $y = x$ 和 $y = x^2$ 之间的最大次数。

三次多项式与一次多项式

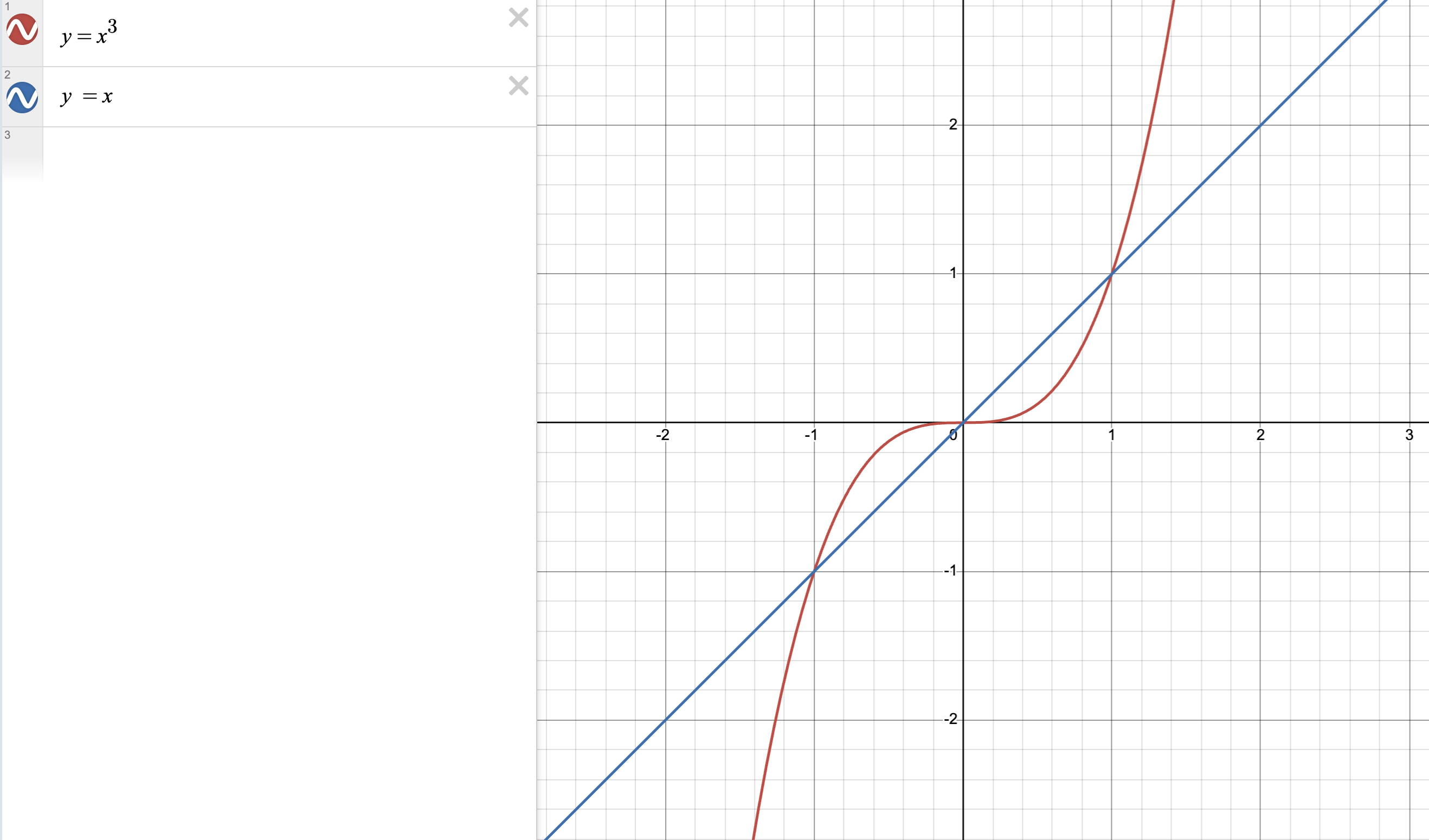
考虑多项式 $p(x) = x^3$ 和 $q(x) = x$。这些多项式在 $x = -1$、$x = 0$ 和 $x = 1$ 处相交，其余地方不相交。交点的数量受多项式最大次数的限制，本例中为 3。

有限域中的多项式与 Schwartz-Zippel 引理

Schwartz-Zippel 引理适用于有限域中的多项式（即所有计算都是对一个质数 $p$ 取模）。

多项式相等性测试

我们可以通过检查它们的所有系数是否相等来测试两个多项式是否相等，但这需要 $\mathcal{O}(d)$ 的时间，其中 $d$ 是多项式的次数。

如果我们能在一个随机点 $u$ 处评估多项式并在 $\mathcal{O}(1)$ 的时间内比较评估值，则会更快。

也就是说，在有限域 $\mathbb{F}_{p}$ 中，我们从 $[0,p)$ 中随机选择一个值 $u$。然后我们评估 $y_f=f(u)$ 和 $y_g=g(u)$。如果 $y_f = y_g$，那么以下两种情况之一必须成立：

1. $f(x) = g(x)$
2. $f(x) \neq g(x)$ 并且我们选择了它们相交的 $d$ 个点之一，其中 $d = \mathsf{max}(\deg(f), \deg(g))$

如果 $d \ll p$，那么第二种情况的可能性极小，可以忽略不计。

例如，如果域 $\mathbb{F}_{p}$ 的 $p \approx 2^{254}$（略小于 uint256），并且如果多项式的次数不超过一百万，那么选择一个它们相交的点的概率为

$$ \frac{1\times 10^6}{2^{254}} \approx \frac{2^{20}}{2^{254}} \approx \frac{1}{2^{234}} \approx \frac{1}{10^{70}} $$

为了对比这个概率的大小，宇宙中原子的数量大约在 $10^{78}$ 到 $10^{82}$ 之间，因此如果多项式不相等，我们选择一个它们相交的点的概率是极其低的。

使用 Schwartz-Zippel 引理测试两个向量是否相等

我们可以将拉格朗日插值与 Schwartz-Zippel 引理结合起来，来测试两个向量是否相等。

通常，我们会通过比较向量的 $n$ 个分量是否相等来测试向量相等性。

相反，如果我们使用一组共同的 $x$ 值（例如 $[1,2,..,n]$）来对向量进行插值：

1. 我们可以为每个向量插值一个多项式 $f(x)$ 和 $g(x)$
2. 选择一个随机点 $u$
3. 在 $u$ 处评估多项式
4. 检查 $f(u) = g(u)$ 是否成立

尽管计算多项式需要更多的工作，但最终的检查要便宜得多。

以下是在 Python 中执行此计算的示例：

import galois
import numpy as np

p = 103
GF = galois.GF(p)

xs = GF(np.array([1,2,3]))

## 任意向量
v1 =  GF(np.array([4,8,19]))
v2 =  GF(np.array([4,8,19]))

def L(v):
    return galois.lagrange_poly(xs, v)

p1 = L(v1)
p2 = L(v2)

import random
u = random.randint(0, p)

lhs = p1(u)
rhs = p2(u)

## 只需要一次检查
assert lhs == rhs

在 ZK 证明中使用 Schwartz-Zippel 引理

我们的最终目标是让证明者向验证者发送一小段数据，验证者可以快速检查它。

大多数情况下，ZK 证明本质上是一个在随机点处评估的多项式。

我们面临的困难是我们不知道多项式是否被诚实地评估——我们必须以某种方式相信证明者在评估 $f(u)$ 时没有撒谎。

但在我们解决这个问题之前，我们需要了解如何将一个完整的算术电路表示为一组在随机点处评估的少量多项式，这是二次算术程序的动机。

• 原文链接： rareskills.io/post/schwa...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～