Circom 之 Hello World

介绍

本章展示了 Circom 代码与其编译成的 Rank 1 Constraint System (R1CS) 之间的关系。

理解 R1CS 对于理解 Circom 至关重要，所以如果你还没有复习过 Rank 1 Constraint System，请务必复习一下。

为了解释 Circom 的工作原理，我们将从几个例子开始。

示例 1：简单乘法

假设我们正在创建 ZK 证明，以评估某人是否知道两个任意数字的乘积：c = a * b。

换句话说，对于某些 a 和 b，我们希望验证用户是否计算出了 c 的正确值。

用伪代码表示，验证如下（注意，这不是 Circom 代码）：

def someVerification(a, b, c):
  res = a * b 
  assert res == c, "invalid calculation"

因此，我们的 R1CS 只有一个约束，即以下约束：

assert c == a * b

R1CS 以结构化的矩阵格式表达这样的约束。根据我们在 R1CS 章节 中看到的内容，见证向量 $\mathbf{w}$ 应该写成 [1, a, b, c]，并且相应的 R1CS 可以写成：

$$ \begin{bmatrix} 0&1&0&0\\ \end{bmatrix}\mathbf{w} \circ \begin{bmatrix} 0&0&1&0\\ \end{bmatrix}\mathbf{w} = \begin{bmatrix} 0&0&0&1\\ \end{bmatrix}\mathbf{w} $$

如果 a = 3, b = 4, 并且 c = 12, 上面的操作将会是：

$$ \begin{bmatrix} 0&1&0&0\\ \end{bmatrix} \begin{bmatrix} 1\\ 3\\ 4\\ 12\\ \end{bmatrix} \circ \begin{bmatrix} 0&0&1&0\\ \end{bmatrix}\begin{bmatrix} 1\\ 3\\ 4\\ 12\\ \end{bmatrix} = \begin{bmatrix} 0&0&0&1\\ \end{bmatrix}\begin{bmatrix} 1\\ 3\\ 4\\ 12\\ \end{bmatrix} $$

以下是如何在 Circom 中编写上述约束：

template SomeCircuit() {
  // inputs
  signal input a;
  signal input b;
  signal input c;

  // constraints 
  c === a * b;
}

component main = SomeCircuit();

• 给定输入 a、b、c，电路验证 a * b 是否确实等于 c。
• 该电路用于验证，不是 用于计算。这就是为什么 c（计算的输出）也是所需的输入之一。
• === 运算符以先前在 R1CS 形式中表达的方式定义约束。=== 的行为类似于断言，因此如果提供无效输入，电路将不满意。在上面的代码中，c === a * b 约束 c 的值等于 a 和 b 的乘积。

zkRepl，一个 Circom 在线 IDE

对于快速实验，zkRepl 是一个非常棒且方便的工具。

我们可以通过将输入作为注释提供，来方便地在 zkRepl 中测试上面的代码：

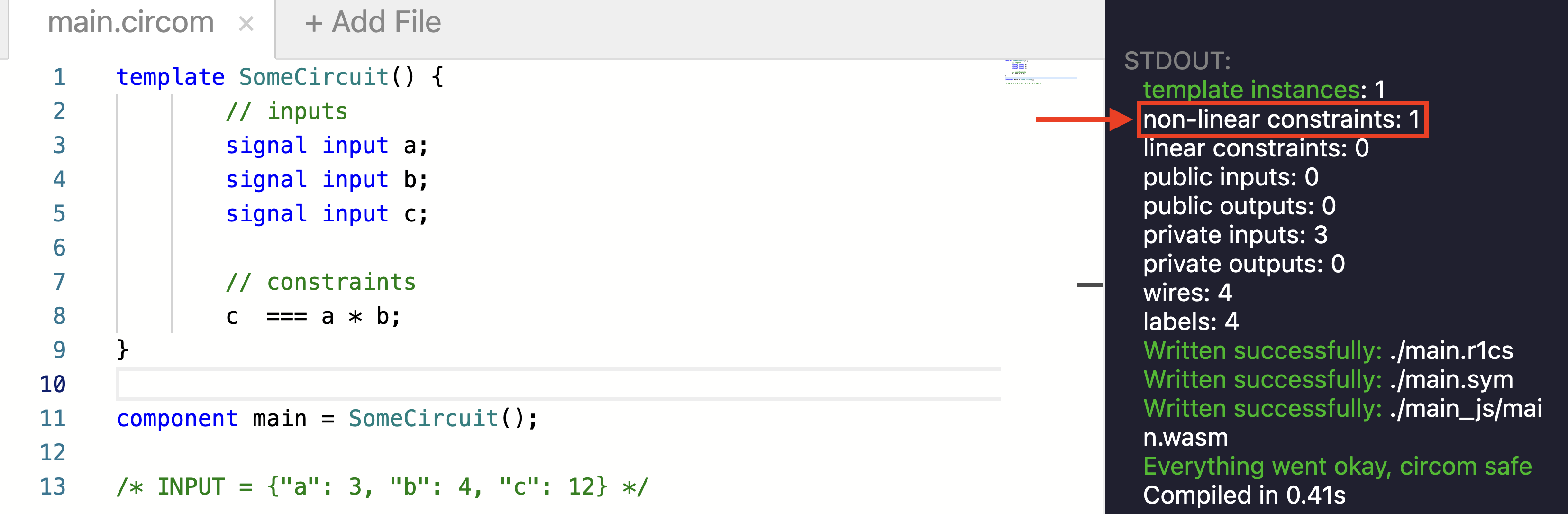
注意： 使用 zkrepl 时，输入作为 JSON 对象在注释中提供。要测试代码是否编译以及输入是否满足电路，请使用 shift-enter。

“非线性约束”等于 1（参见红色框），因为底层 R1CS 具有一行约束，其中包含两个信号之间的乘法。这是预期的，因为我们只有一个 ===。

template , component , main

• Templates (模板) 定义了电路的蓝图，就像类定义了 OOP（面向对象编程）中对象的结构一样。
• Component (组件) 是模板的实例化，类似于对象是面向对象编程中类的实例。

// create template
template SomeCircuit() {
  // .... stuff
}

// instantiate template 
component main = SomeCircuit();

需要 component main = SomeCircuit()，因为 Circom 需要一个顶层组件 main 来定义要编译的电路结构。

signal input

• Signal inputs (信号输入) 是将从组件外部提供的值。(Circom 不强制实际提供一个值 —— 这取决于开发人员来确保实际提供这些值。如果它们没有提供，这可能会导致安全漏洞 —— 这将在后面的章节中探讨。)
• 输入信号是不可变的，不能被更改。
• 信号正是 Rank 1 Constraint System 见证向量中的变量。

Circom 的有限域

Circom 在一个 有限域 中执行算术运算，其阶数为 21888242871839275222246405745257275088548364400416034343698204186575808495617，我们将其简称为 $p$。它是一个 254 位数字，对应于 bn128 椭圆曲线的曲线阶数。该曲线被广泛使用，特别是在 EVM 中通过预编译提供该曲线。由于 Circom 旨在用于开发以太坊上的 ZK-SNARK 应用程序，因此使字段大小与 bn128 曲线的曲线阶数匹配是有意义的。

Circom 允许通过命令行参数更改默认顺序。

以下内容对于读者来说应该是很明显的：

• p 在 mod p 下与 0 同余；
• p-1 是 有限域 mod p 中最大的整数。
• 传递大于 p-1 的值将导致溢出。

示例 2：BinaryXY

让我们看第二个例子来结束本节。

考虑一个电路，该电路验证传递给它的值是否为二进制，即 0 或 1。

如果输入变量是 x 和 y，则约束系统将是：

(1):  x * (x - 1) === 0
(2):  y * (y - 1) === 0

回想一下，根据定义，R1CS 中的每个约束最多只能有一个变量之间的乘法。

• x (x-1) === 0 检查 x 是否为二进制数字

• 这个多项式表达式只有 2 个根。

• I.e., x = 0 或 x = 1.

用 Circom 表示

template IsBinary() {

  signal input x;
  signal input y;

  x * (x - 1) === 0;
  y * (y - 1) === 0;
}

component main = IsBinary();

替代表达方式：使用数组

在 Circom 中，我们可以选择将输入声明为 separate signals (单独的信号)，或者声明一个包含所有输入的 array (数组)。在 Circom 中，更常见的是将所有输入分组到一个名为 in 的信号 array (数组) 中，而不是提供单独的输入 x 和 y。

按照惯例，我们将之前的电路表示如下。数组的索引从零开始，正如你通常期望的那样：

template IsBinary() {

  // array of 2 input signals
  signal input in[2];

  in[0] * (in[0] - 1) === 0;
  in[1] * (in[1] - 1) === 0;
}

// instantiate template 
component main = IsBinary();

只有满足约束的见证才会被接受

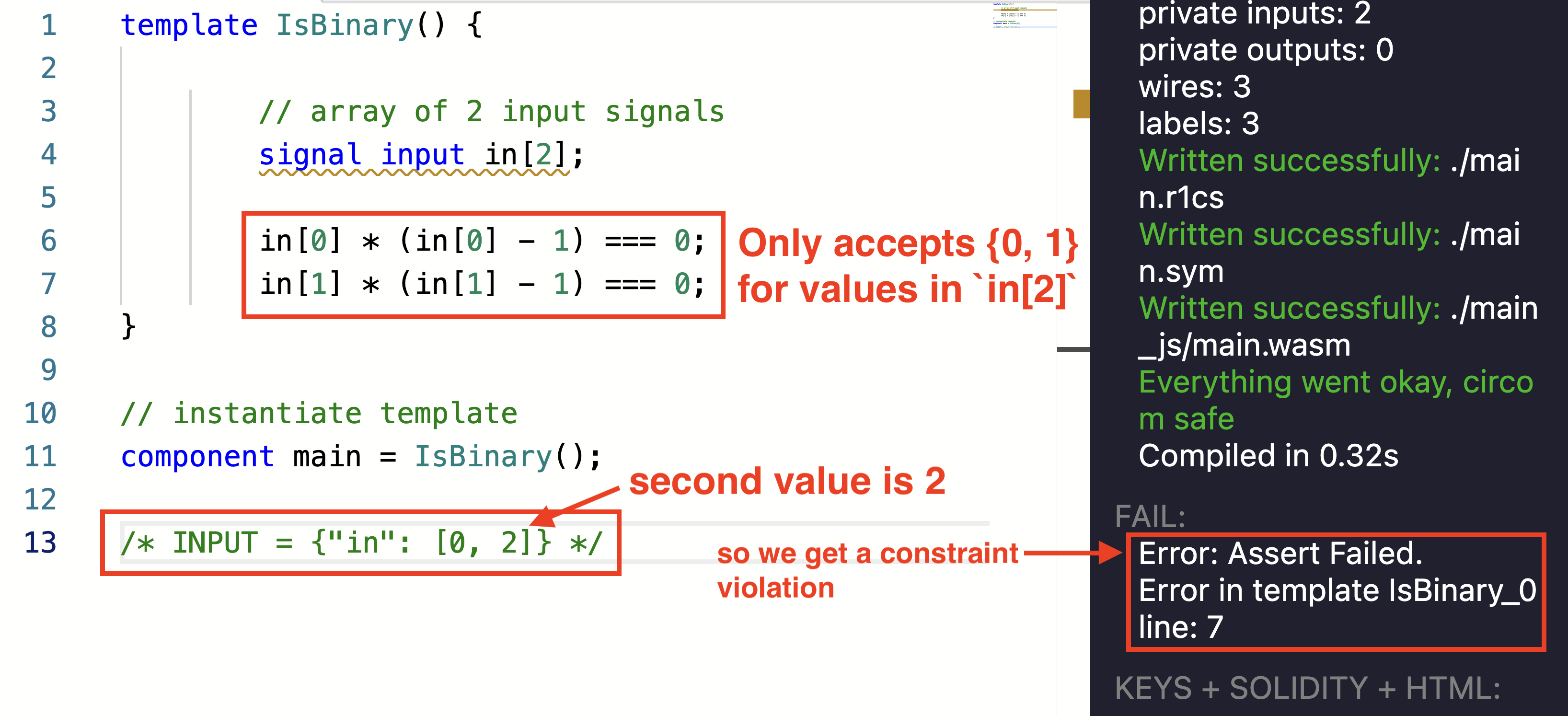
Circom 只能为实际满足电路的输入生成证明。在以下电路（直接从上面的代码复制）中，我们提供 [0, 2] 作为输入，该输入仅接受 {0,1} 作为数组的任何元素。

对于 0，我们有 0 * (0 - 1) === 0，这是可以的。但是，对于 2 * (2-1) === 2，我们有一个约束冲突，如下图中的红色框所示。

在命令行中使用 Circom

本节介绍常用的 Circom 命令。我们假设读者已经安装了 Circom 和所需的依赖项。

创建一个新目录，并在其中添加一个名为 somecircuit.circom 的文件，其中包含以下...